
Research and Development of a Technological Process and Stamping
Equipment for Radial Extrusion of the “Picabur Body” Part
Fatkhulla Abdullaev
a
, Shakhrukh Akhmadaliyev
b
, Kamoliddin Khasanov
c
and Rufat Abdullaev
d
Tashkent State Technical University, 100095, University str. 2, Tashkent, Uzbekistan
Keywords: Radial Extrusion, Contour Upsetting, Stamping.
Abstract: The article talks about the production of the “Picabur Body” part using resource-saving extrusion stamping
technology. The energy method and the finite element method were chosen as the research method. A
kinematic version of the methods of radial extrusion with contour upsetting and a design diagram of the radial
extrusion process are given. The deformation center and stress-strain state during extrusion stamping of the
above part are determined. The mechanism and sequence of filling the working cavity of the die are revealed.
The scheme of the die and its main working elements during extrusion stamping of the Pickabur Body are
also given. The principle of operation of die tooling and technological equipment, which was used in radial
extrusion stamping, is described.
1 INTRODUCTION
In developed countries, the development of heavy,
mining, and light industries has a positive effect on
the economy of their countries. In the manufacture of
“Picabur body”, widely used in various branches of
mechanical engineering, with flanges or thickenings
of various configurations, one of the promising
technologies is cold radial extrusion. A feature of
radial extrusion technology is the ability to actively
regulate the deformation and force parameters of the
process by changing the kinematics of movement of
the forming tool. Quite a lot of work has been devoted
to studying the process of radial extrusion. However,
practically until now the influence of nonmonotonic
deformation in the processes of cold radial extrusion
has not been considered. New combined methods of
radial extrusion, which themselves contribute to the
healing of damage to metals during deformation, have
practically not been developed or investigated. The
resulting gap hinders the implementation of cold
radial extrusion processes for the production of rod
parts with a wide flange. One of these new combined
a
https://orcid.org/0000-0002-3934-9336
b
https://orcid.org/0000-0002-4188-0126
c
https://orcid.org/0000-0000-2838-9028
d
https://orcid.org/0009-0009-4352-1138
methods of cold die forging is the method of radial
extrusion with contour upsetting, which is being
developed taking into account the effective use of
non-monotonic deformation. When developing new
combined extrusion methods, it is necessary to
determine the force mode, evaluate the deformability
of the workpiece and determine their advantage. At
present, technological processes of radial extrusion
with contour upsetting have not yet been studied.
In this regard, the study of the technological
process of radial extrusion from the “Picabur body”
is an urgent problem.
2 MATERIALS AND METHODS
In the world improvement of product quality and
labor in the engineering industry speeding up
production due to increased productivity the
occurrence of the process is of particular importance.
At the same time bending of the surface layer of metal
in the production of tools One of the important tasks
is to increase the endurance and operational time is
294
Abdullaev, F., Akhmadaliyev, S., Khasanov, K. and Abdullaev, R.
Research and Development of a Technological Process and Stamping Equipment for Radial Extrusion of the “Picabur Body” Part.
DOI: 10.5220/0014262600004738
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 4th International Conference on Research of Agricultural and Food Technologies (I-CRAFT 2024), pages 294-300
ISBN: 978-989-758-773-3; ISSN: 3051-7710
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

considered. The material for the research was the
picabur body, which is produced by extrusion
stamping from St3 steel at Geoburtechnica.
3 RESULTS AND DISCUSSION
The method is based on the theory of plastic flow,
since it allows one to determine the kinematic, stress
and deformation states at any point in the zone of
plastic deformation, and take into account anisotropy,
non-stationarity and the history of deformation. The
following basic assumptions are used: the material is
considered rigid-plastic, and strain or rate hardening
is taken into account by the average value of the yield
stress over the deformation zone; Contact friction
forces during ordinary extrusion obey Siebel's law,
and when extruding with active friction forces, they
obey Amonton's law.
Theoretical analysis is carried out in the following
sequence:
1. The source of plastic deformation of the
workpiece is divided into areas convenient for setting
the field of suitable flow velocities in them. The
specified expressions for flow rates can include both
specific dependences, justified experimentally, and
functions of a general form
v
x
= v
x
(x, y, z, t),
v
y
= v
y
(x, y, z, t),
v
z
= v
z
(x, y, z, t), (1)
At the boundaries between regions, the continuity
condition can be observed in a relaxed form,
satisfying the condition of constant flow in integral
form.
2. Based on the flow rates (1), the components of the
strain rate are found:
ξy =
(
+
). (2)
3. Each region contains the intensity of strain rates.
ξ
1
=
𝜉
𝜉
(3)
If it is necessary to simplify the solution, the value
of the strain rate intensity is averaged over one or
several coordinates and in the process of further
analysis is considered independent of these
coordinates.
4. Expressions (2) and (3) are substituted into the
equations for the relationship between stresses and
strain rates
σ
y
=𝜕
𝜎+
𝜉
(4)
Where 𝜕𝑦 - Kronecker symbol.
5. From the joint solution of the system of equilibrium
equations
= 0,
(5)
taking into account expressions (4), the stresses
are found. Arbitrary integration constants are found
from the boundary conditions. If necessary, to
simplify the solution of the system, the Huber-Mises
energy plasticity condition is used in the form
σ
ii (max)
– σ
jj (min)
= βσ
3
(6)
where β is the Lode coefficient, which for an
isotropic material is taken equal to its average value β
= 1, 1.
The use of a simplified plasticity condition that
does not take into account the tangential stresses
instead of the flow law associated with the exact
energy condition is not a disadvantage, since, on the
one hand, it allows one to avoid a decrease in
accuracy using approximate integration methods, and
on the other hand, the analysis showed that all the
main terms obtained from the proposed method, the
stress formulas coincide with those obtained on the
basis of the associated flow law, and the minor terms
give a slight overestimation of the result, which,
firstly, is consistent with the upper estimate method,
and secondly, makes it possible to compensate for the
mismatch of tangents that is always present in the
boundary conditions for non-zero friction stresses,
which cannot be taken into account in existing
momentless theories of plasticity.
6. Based on the found stresses, based on the
coupling equations (4) and kinematic boundary
conditions, the specific form of the velocity functions
specified at the beginning of the solution in general
form is determined.
7. If it is necessary to take into account the
anisotropy of the properties of the initial workpiece,
the plasticity condition and the relationship between
stresses and strain rates from the theory of plasticity
of anisotropic Mises -Hill bodies are used. The
analysis of this theory made it possible to introduce
an indicator of the form k = σ
sp
/ σ
sz
(where σ
sz
is the
yield stress along the axis of the workpiece, σ
sp
is the
yield stress in the radial direction), and obtain the
plasticity conditions of an anisotropic body in the
form
Research and Development of a Technological Process and Stamping Equipment for Radial Extrusion of the “Picabur Body” Part
295

𝜎
− 𝜎
= β𝜎
,
𝜎
− 𝜎
= β𝜎
.
(7)
In these expressions, the coefficient values are in the
interval
k≤ 𝛽≤2 /
√
4− 𝑘
at k<1, interval k≤ 𝛽≤
2 /
√
4− 𝑘
k >1.
If k = 1, then the interval of change of the
coefficient P completely coincides with the interval of
change of the Lode coefficient used in the theory of
plasticity of an isotropic body
8. A.A. Ilyushin’s formula is integrated, relating the
strain rate to the accumulated strain
ξi
_
=
=
+𝑣
+ 𝑣
+ 𝑣
, (8)
resulting in accumulated deformation
e
i
= f (x , y , z) (9)
where C - is an arbitrary constant.
9. Lagrange expressions are integrated
v
x
=(x , y , z , t)=
v
x
=(x , y , z , t)=
v
x
=(x , y , z , t)=
(10)
As a result, the dependences of the current
coordinates of the particle (Eulerian coordinates) on
the initial coordinates (Lagrange coordinates) and
time are found:
x = ψ
1
(x
0
, y
0
, z
0
, t )
y = ψ
2
( x
0
,y
0
,z
0
,t)
z = ψ
3
(x
0
,y
0
,z
0
,t) (11)
10. Using expressions (11), the initial coordinates of
the particle are determined from the condition 𝑒=𝑒
,
for 𝑒=𝑒
, 𝑥=𝑥
, 𝑦=𝑦
, t = 0, 𝑧=𝑧
. An
arbitrary constant value e
0 is found
, taking into account
the history of deformation;
e
10
=0, if the original workpiece has no accumulated
deformation. For convenience, you can replace the
time with the punch stroke
s=v
0
t (12)
where v
0
is the speed of movement of the punch.
11. Using expressions (11), the sizes of zones in
which material points in the process of deformation
pass the same path are determined; the deformation
field in such zones is stationary.
12. If necessary, the directions of the fibers of the
macrostructure are found using expressions (11). By
taking the initial coordinates of any material point of
any fiber of interest to the researcher and substituting
them into expressions (11), it is possible to determine
where this point will move at a certain value of the
working stroke s. By repeating this procedure for a
sufficient number of points on a single fiber, the shape
and position of that fiber macrostructure in the
stamped product can be determined.
13. For a certain value of the working stroke,
according to formula (9), the average value of the
accumulated deformation in the zone of plastic
deformation is calculated, from which the average
value of the yield stress of the workpiece is
determined.
14. To determine the size of the source of plastic
deformation, the principle of minimum specific
deforming force (minimum of the total deformation
energy) is used. For a hardening material,
minimization is carried out taking into account the
dependence of the average yield stress on the
accumulated deformation, which in turn depends on
the size of the source. The shape of individual flanges
of the site of plastic deformation is determined by
found expressions for flow velocities.
16. As a result of such calculations, a diagram of
the change in force during extrusion is constructed,
showing the effect of hardening of the workpiece
material on the force characteristics of the process.
15. To obtain intercomparable solutions suitable
for determining the optimal geometry of the tool, it is
necessary to satisfy the following requirements when
fulfilling points 1 and 5: design schemes, kinematics
and boundary conditions must transform into one
another in the limiting cases of different tool shapes.
The final criterion for checking intercomparability is
the comparison of formulas specific deforming force
in related cases of different tool shapes. In order to
expand the applicability of formulas, for hollow
products it is advisable to choose calculation schemes
suitable for analysis not only at the quasi-stationary
stage of extrusion, but also under bottom effect
conditions.
The process of radial extrusion is divided into two
stages (Fig. 1.);
- at the first stage, the metal is deformed by
moving the punch at speed 𝑉
in order to form a
thickening in some part of the product;
I-CRAFT 2024 - 4th International Conference on Research of Agricultural and Food Technologies
296
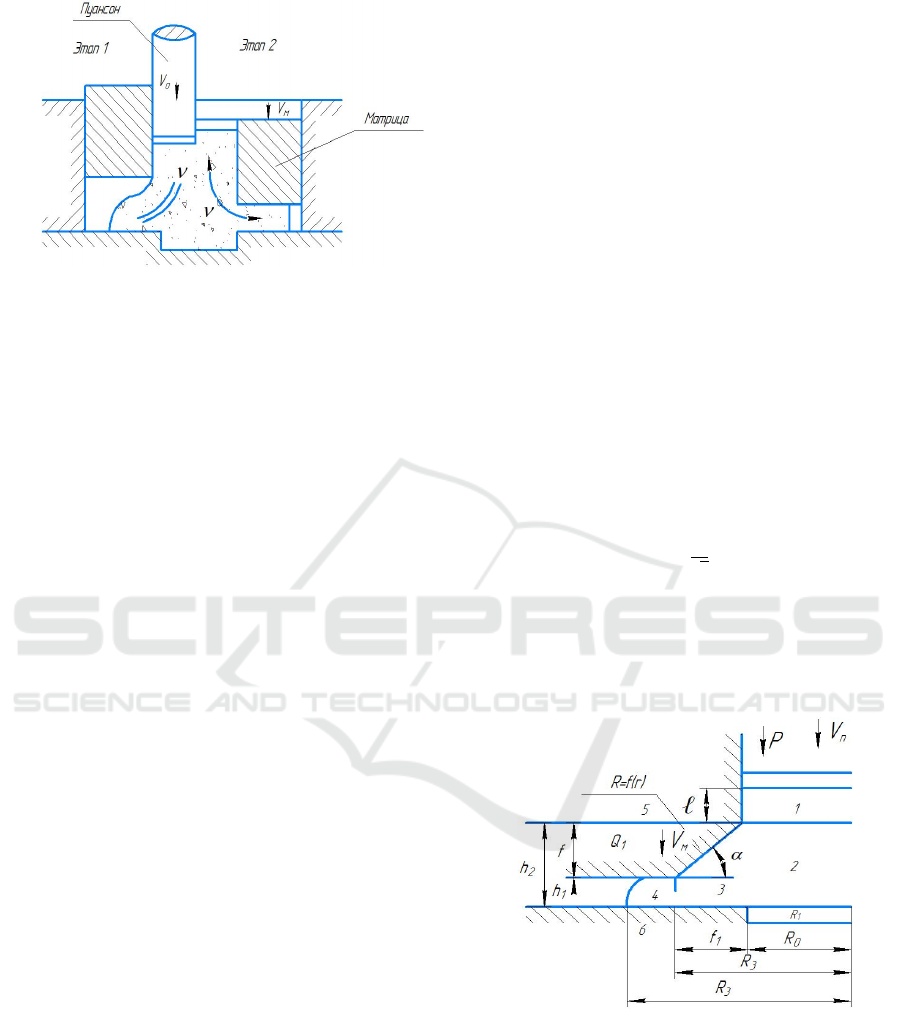
Figure 1: Kinematic version of radial extrusion methods
with contour upsetting.
- at the second stage, only such a separate
thickening is deformed with forced movement of the
matrix at speed 𝑉
м
, subject to the release (removal) of
the punch. It is the removal of the punch at the second
stage that creates the opportunity to control by
deformation. Due to the fact that at the second stage
only the contour part of the thickening is deposited,
this process is called the “extrusion process with
contour settlement”.
It was established that when studying the force
regime and deformability for the process of radial
extrusion (as the first stage of fishing with contour
settlement), the influence of the angle of the straight
transition edge was not sufficiently clarified.
The entire process of deformation by extrusion
with contour upsetting is divided into two stages: and
the first stage occurs as usual radial extrusion and is
called “upsetting by extrusion.” For the first stage, the
force mode was analyzed taking into account the
influence of the angle of the straight transition edge.
The energy method makes it possible to take into
account the main features of the process and
simultaneously determine both the active deforming
force developed by the punch and the reactive force
perceived by stationary tools. An upper estimate of
such forces can be obtained from the energy balance
if it includes the powers developed by reactive forces
at the virtual speeds of movement of the
corresponding parts of the tool, and the linearization
of all powers relative to the virtual and specified
speeds of the tool is carried out.
Solutions were carried out using the following
assumptions:
- normal component of the discontinuity
velocity vector, discontinuities have only components
directed along the block boundaries;
- specific contact forces friction on the contact
surface constant and proportional to the flow
resistance of the material;
- the workpiece material is homogeneous and
non-strengthening;
- the speed of the tool is constant.
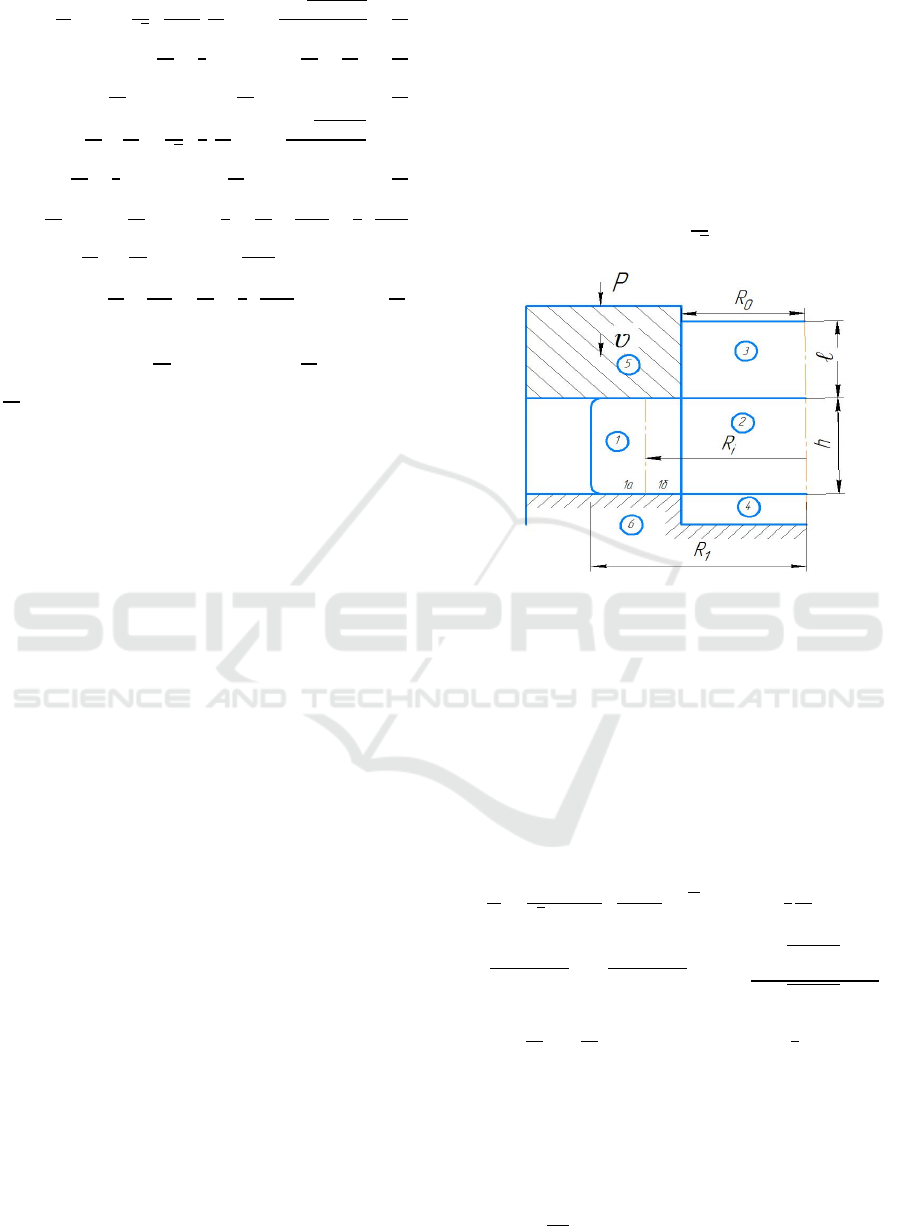
We accept the following kinematic possible
velocity fields, a state of separate rigid blocks and
satisfying the kinematic boundary conditions and the
unexpectedness condition (Fig. 2). The accepted
kinematically possible velocity fields are based on
those established as a result of experimental studies
of the shape and source of plastic deformation.
The forces of deformation and opening were
determined from the power balance equation of
external and internal forces at kinematically possible
speeds of movement:
𝜌 𝜗
𝜋𝑅
+𝑞𝑣
𝜋
(
𝑅
−𝑅
)
=𝑊
+𝑊
+𝑊
(13)
where: - power of plastic deformation in zones 2,3,4:
𝑊
=∑𝑊
=∑6
∭6
𝑑𝑣; (14)
- power of shear forces on the velocity discontinuity
surfaces between zones 1-2, 2-3, 2-6, 3-4:
𝑊
с
=∑𝑊
с
=∑
√
∬
𝑢
𝑑𝑠; (15)
- power of contact friction forces on the surfaces of
contact with the tool: 1 and 5, 3 and 5, 4 and 5:
𝑊
=∑𝑊
=∑𝜇6
∬
𝑢
𝑑𝐶. (16)
Figure 2: Calculation diagram of the radial extrusion
process
Having calculated the powers of the forces of
plastic deformation, shear and contact friction,
substituting the found power values and the power
balance equation 1, separating the terms containing
𝑣
and 𝑣
м
we get:
Research and Development of a Technological Process and Stamping Equipment for Radial Extrusion of the “Picabur Body” Part
297
=1+
√
+ 2𝜇
𝑙𝑛
+
2𝑙𝑛
+
𝑡𝑔𝜎+ 2𝜇
−
−
+
1,14
2𝑙𝑛
+0,5𝑦−1𝑛
+0,2𝑡𝑔𝜎
2𝑙𝑛
−
𝑙𝑛
;
=
√
+2𝜇
(
𝑠
−
𝑡𝑔𝜎
)
𝑙𝑛
−
𝑦 𝑡𝑔
𝜎−𝑠
−1
𝑡𝑔𝜎 + 2𝜇
−
+2𝑙𝑛
+1,14
𝑙𝑛
−
+
−
1
ln
+
𝑦𝑡𝑔𝜎 + 2
+0,2 0,5𝑡𝑔𝜎−
−
𝑙𝑛
+
− 𝑡𝑔𝜎
𝑙𝑛
(17)
Where 𝑦=
−1; 𝑥=1+
; 𝑠=𝑡𝑔𝜎+
.
The second stage of the extrusion process with
contour upsetting represents the stages of contour
upsetting of the thickening formed at the first stage,
provided there is a movable punch. Design diagrams
are shown (in Fig. 3).
From the analysis of experimental studies, it was
established that the change in the dimensions of the
workpiece occurs in two stages:
1 - upsetting of the workpiece without changing
the length of the workpiece rod (size l), as long as the
dimensions of the workpiece or the friction conditions
are such that 𝑅
<𝑅
( 𝑅
is the radius of the
separation boundary of the metal flow). This is the
initial stage in the case of a large cavity height.
2-combination of the settlement of the annular
part of the workpiece with the formation of a rod, the
total height of which continuously increases if the
dimensions of the workpiece lead to the value 𝑅
>
𝑅
. This corresponds to the last stages with a decrease
in the height of the cavity (or as the matrices approach
each other).
An analysis of the power mode for the second
stage, which has more important implications for the
analysis of the technological characteristics of this
process, was carried out. The assumptions discussed
above are used. We accept the following kinematic
possible velocity fields, consisting of individual rigid
blocks and satisfying the boundary conditions and the
incompressibility condition. The accepted
kinematically possible velocity fields are based on the
shape and source of plastic deformation established
as a result of experimental studies.
The energy balance equation will be written as:
р 𝑣
𝜋
(
𝑅
−𝑅
)
=𝑊
+𝑊
+𝑊
(18)
where 𝑊
is the power of plastic deformation in
zones 1 and 2
𝑊
=∑𝑊
=∑6
∭6
𝑑𝑣
- the power of shear forces on the velocity
discontinuity surfaces between zones 1-2; 2-3 and 2-
4;
𝑊
с
=∑𝑊
с
=∑
√
∬
𝑢
𝑑𝑠; (19)
Figure 3: Design diagram for the second stage.
- power of contact friction forces on contact
surfaces 1 and 3 with tool 5
𝑊
=∑𝑊
=∑𝜇6
∬
𝑢
𝑑𝑐; (20)
Substituting all the found values of powers and
transformations into the energy balance equation (4),
we obtained a formula for determining the relative
specific deformation force:
=
√
√
3
𝑅
+𝐻+
+ℎ𝑅
+
𝑅
+3𝑅
−
𝑅
+3𝑅
−𝑅
𝑙𝑛
+
4𝜇
𝑙
+4
𝑅
(
2𝑅
−𝑅
−𝑅
)
+
(
𝑅
+𝑅
−
−2𝑅
)
(21)
The varying radius of metal separation
determination R
1
is determined by solving the
equation
Р
Р
=0.
I-CRAFT 2024 - 4th International Conference on Research of Agricultural and Food Technologies
298
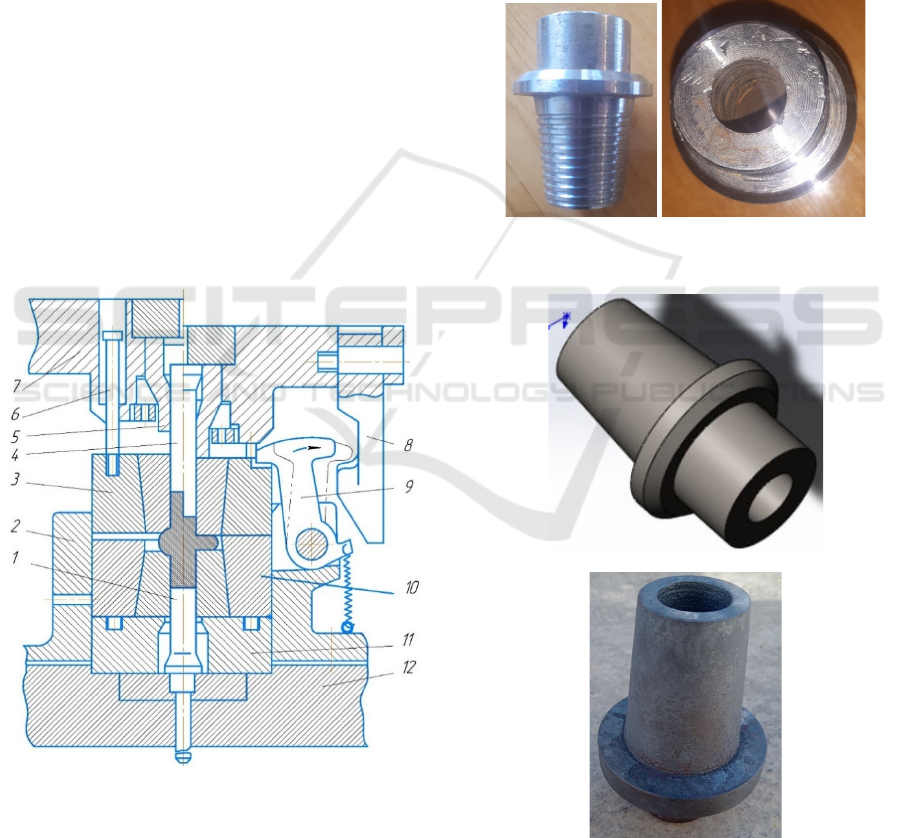
The stamp for this part has its own characteristics.
The matrix is made of two parts with a horizontal
connector plane. The receiving cavity is made in one
of the semi-matrices. The basic scheme of the die for
radial extrusion is shown in Fig. 2. The stamp is made
of steel 5ХНМ. Molybdenum disulfide with mineral
oil was used as a lubricant.
The die contains a punch 4 mounted on the upper
movable plate 7 with a pressure sleeve 5 covering it,
as well as an upper half-matrix 3 connected to the
plate 7 by means of rods 6. On the lower plate 12 is
mounted matrix holder 2, in which is installed the
lower half-matrix 10. In the vertical cavity of the half
matrix 10 is placed counter punch 1, covered by a
support sleeve 11. When clamped together, the half-
matrixes form a working annular cavity. The
mechanism of locking of the half-matrixes after their
clamping is made in the form of at least two hinged
(as a rule attached to the matrix holder) 2 rotary (in
the vertical or horizontal plane) spring-loaded levers
9. The levers interact their working front edge with
the upper end of the upper half-matrix 3. The rear side
of each of the locking levers interacts with the drive
mechanism, made in the form of, for example, a
pneumatic cylinder or a spring-loaded pusher 8,
hinged to the movable plate 7.
Figure 4: Schematic diagram of a die for radial extrusion
After clamping the half-matrixes, they are locked
by levers rotated by the pushers. Half-matrixes under
the action of metal extruded into the transverse cavity
and sawing forces are extended to contact with the
working edge of the levers 9. At the final stage of
deformation, the sleeve 5 comes into contact with the
half-matrix 3 and moves it downwards synchronously
with the punch, which leads to a decrease in the cavity
height and metal deposition in the flange area. This
frees the levers 9, which due to springing are
accelerated back to the initial position and do not
prevent the lifting of the upper half-matrix with the
movable plate 7 during the idle stroke of the press
slide.
Taking into account all the above calculations, it
was decided to test the theoretical research data in
practice. As a result of the experimental work, the
following results were obtained (Fig. 5; 6):
Figure 5: General view of the “Pikabur body” obtained by
cutting
Figure 6: Forging produced by precision stamping by radial
extrusion with contour upsetting
Research and Development of a Technological Process and Stamping Equipment for Radial Extrusion of the “Picabur Body” Part
299

4 CONCLUSIONS
1. A new method of extrusion with contour upsetting
has been developed, which uses the positive effect
of the influence of non-monotonic deformation on
the ultimate shape change of workpieces. The
main technological parameters of the processes
are established on the basis of studies of the force
regime, stress-strain state and workpiece
deformability.
2. Experiments on force modes were carried out to
verify the reliability of the theoretical calculation.
The discrepancy between calculated and
experimental data in most cases did not exceed
20-25%.
REFERENCES
Abdullaev, F. S., Akhmadaliev, Sh. Sh., Zagidullin, R. R.,
& Ismailov, Kh. U. (2021, December). Mathematical
model of axisymmetric flow in the extraction of a drill
body "pickabur" used in drilling operations.
International scientific and scientific-technical
conference on “Practical and innovative scientific
research: current problems, achievements and
innovations (dedicated to the memory of professor
A.A.Yusupkhodjaev)” 6 th December, 2021 (p. 300).
Abdullaev, F. S., Zagidullin, R. R., & Akhmadaliev, Sh. Sh.
(2021). Analyz metoda dozirovaniya iskhodnyx
zazhetok po masse. Universum: technical science, (1-
1), 31-33.
Abdullaev, F. S., Zagidullin, R. R., & Akhmadaliev, Sh. Sh.
(2021). Analyz metoda dozirovaniya iskhodnyx
zazhetok po masse. Universum: technical science, (1-
1), 31-33.
Abdullayev, F. S., Khasanov, K. A., & Abdullayev, R. F.
(2021, December). Pikabur body detail and stamp
project for its production. International scientific and
scientific-technical conference on “Practical and
innovative scientific research: current problems,
achievements and innovations (dedicated to the
memory of professor A.A.Yusupkhodjaev)” 6 th
December, 2021 (p. 307).
Akhmadaliev, Sh. Sh., Zagidullin, R. R., & Usmonjonov, S.
I. (2021, December). Experimental equipment for
obtaining a "pickabur" used in drilling operations.
International scientific and scientific-technical
conference on “Practical and innovative scientific
research: current problems, achievements and
innovations (dedicated to the memory of professor
A.A.Yusupkhodjaev)” 6 th December, 2021 (p. 295).
Aliev I. S. Teoretichesky analysis of the process of
combinirovannogo radialnogo obratnogo
vydavlivaniya /I. S. Aliev, N. S. Grudkina // Obrabotka
metallov davleniem: sb. Nauch. tr. – Kramatorsk:
DGMA, 2008. – No. 1 (19). - S. 55–60.
Alieva L. I Perspektive razvitiya protsesov tochnoy
obemnoy shtampovki vydavlivaniem / L. I. Alieva, Ya.
G. Zbankov // Visnik DDMA. – 2008. – No. 1 (11). - S.
13-19.
Golenkov V.A. Teoriya obrabotki metallov davleniem:
uchebnik dlya vuzov / V.A. Golenkov, S.P. Yakovlev,
S.A. Golovin, S.S. Yakovlev, V.D. Kuhar. Pod ed. V.A.
Golenkova, S.P. Yakovleva. - M.: Mashinostroenie,
2009. - 442 p
Khasan, I., Fatkhulla, A., Shahkrukh, A., & Rafail, Z.
(2021). Determination of the stress-strain state by
stamping extrusion of axisymmetric parts. International
Journal of Mechatronics and Applied Mechanics, (10),
123-128.
Vorontsov A. L. Analytic study of combined discharge of
dissimilar materials in the extrusion of rod-like articles.
Russian Engineering Research, 2000, vol. 20, № 11, pp.
47–51.
I-CRAFT 2024 - 4th International Conference on Research of Agricultural and Food Technologies
300
