
Mathematic Modelization of the Absorption of Water Drop by Wind
in the Rainbowing Irrigation of Agricultural Crops
Zafar Khudayorov
a
Tashkent State Agrarian University, 100140, University str. 2, Tashkent, Uzbekistan
Keywords: Rain Irrigation, Water Drop Trajectory, Wind Influence.
Abstract: The article takes a mathematical model of the process of blowing a drop of water under the influence of the
wind when raining and watering agricultural crops. Graphs of the movement trajectory of a water drop in a
changing environment are built, the influence of wind speed and direction on the process is analyzed. To
improve the raining process, methods have been developed to increase the effective irrigation coefficient, on
which the technological and structural parameters of raining machines are based
.
1 INTRODUCTION
Due to the change in the size of the artificial water
drop formed by rainmaking machines in the range of
0.8-3.5 mm, due to the rise of water particles from the
ground level to 4-4.5 meters,evaporation of the water
drop and wind blowing increase, on windy days, the
effective irrigation coefficient decreases from 0.76-
0.80 to 0.45-0.5. Waste of Water Resources in rainfall
can reach 22-24 percent, in some cases up to 40
percent (Sevryugin, 1998; Zhelyazko et al., 2015;
Khudayorov, 2022; Khudayorov et al., 2023a). It is
relevant to reduce the waste of Water Resources,
develop the scientific and technical basis of the
energy-efficient rain irrigation process, improve the
quality indicators of rain irrigation, improve
rainmaking machines and devices, introduce into
design and mechanical engineering practices
(Voronin, 1988; Vinogradov, 2015; Akpasov, 2018;
Khudayorov, 2024a; Khudayorov, 2024b).
2 MATERIALS AND METHODS
The sum of the forces acting on a drop of rainwater is
expressed by the formula on it (Khudayorov et al.,
2023b):
𝑚𝑎⃗
𝑡
=𝑚𝑔⃗−𝑝
𝑉
𝑔⃗−3𝜋𝑑
𝜇𝜗
⃗
𝑡−
𝐶
𝜌
𝑆
𝜗
⃗
𝑡 𝜗
⃗
𝑡.
(1)
a
https://orcid.org/0009-0003-4137-4068
where m- is the mass of the drop of water; a
⃗
t
-
is the vector of acceleration of the drop of water; g -
is the acceleration of free fall; 𝜌
-is the density of
the environment, ambient temperature at t=20 °C is
the air density 𝜌
= 1,2754 kg/m³; V
- is the volume
of the drop of water, m³; μ–coefficient stickness of the
environment: air for μ=1,8·10
-5
Pa, water for μ=10
–3
Pa; 𝑑
-the diameter of the water drop, ϑ
⃗
t-the
absolute value of the vector of the speed of a body,
m/s; π – sharing coefficient and its value depends on
the form of a body which is about equal to 0.4 in the
form of solids; S
– direction transverse incisions of
the movement of solids (midelevoy) surface,
S
=
;
C
- aerodynamic resistance coefficient, sferik in
the form of solids C
=0.5 in.
To represent 𝑎⃗
𝑡
projections of water drop
acceleration in flight
𝐾
𝑡
=−
(2)
by introducing a variable coefficient, we get the
following expressions for its projection on the X and
Y axes:
𝑎
𝑡
=𝐾𝑡𝜗
𝑡
; (3)
𝑎
𝑡
=
−1
𝑔𝐾𝑡 𝜗
𝑡
. (4)
172
Khudayorov, Z.
Mathematic Modelization of the Absorption of Water Drop by Wind in the Rainbowing Irrigation of Agricultural Crops.
DOI: 10.5220/0014225000004738
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 4th International Conference on Research of Agricultural and Food Technologies (I-CRAFT 2024), pages 172-175
ISBN: 978-989-758-773-3; ISSN: 3051-7710
Proceedings Copyright © 2025 by SCITEPRESS – Science and Technology Publications, Lda.

To calculate the resulting equations, we use the
method of time discretization.
Let the speed and acceleration of the rainwater
drop between selected times. If the values of the
velocity vector and acceleration projections within
the time unit 𝑡
are denoted by
𝜗
𝑡
,𝜗
𝑡
,𝑎
𝑡
,𝑎
𝑡
respectively, then the
projections of the velocity vector 𝑡
at the same
time are equal to:
𝜗
𝑡
=1𝐾
𝑡
Δ𝑡𝜗
𝑡
;
(5)
𝜗
𝑡
=
−1
𝑔∙Δ𝑡𝐾
𝑡
∙Δ𝑡∙𝜗
𝑡
,
(6)
The coordinates of the water drop at any time are
determined by the formula:
𝑥
𝑡
= 𝑥
𝑡
𝜗
𝑡
Δ𝑡;
(7)
𝑦
𝑡
= 𝑦
𝑡
𝜗
𝑡
Δ𝑡
. (8)
To determine the wind effect on an artificial water
drop in flight, let's consider the obtained equations (7)
and (8) in a variable environment. The resistance
force of the environment under the influence of wind
has the following appearance:
𝐹
⃗
𝑡
=
𝜗
=
𝜗
𝑡
𝜗
𝑡
−
𝜗
𝑠𝑖𝑛𝜃
, (9)
where ϑ
is the wind speed, m/s; θ is the angle
between the water flow line and the wind direction,
o
.
Given the wind Effect (2) the variable coefficient
of the environment expressed by the formula can be
written as:
𝐾
𝑡
=−
(10)
Taking into account the effect of wind speed on
the speed at which the water drop flies ,we represent
the equation (5) and (6) in the following way:
𝜗
0
=𝜗
⃗
𝑜
𝑐𝑜𝑠𝛼−𝜗
𝑠𝑖𝑛𝜃 ;
𝜗
0
=𝜗
⃗
𝑜
𝑠𝑖𝑛𝛼 .
(11)
Then the mathematical model of the motion
trajectory of a water drop (7) and (8) come to the
following view:
𝑥
𝑡
=1𝐾
𝑡
Δ𝑡𝜗
𝑡
;
(12)
𝑦
𝑡
=
−1 ∙ 9,81 ∙ Δ𝑡 1
𝐾
𝑡
∙Δ𝑡∙
𝜗
𝑡
(13)
3 RESULTS AND DISCUSSION
In the process of rainmaking in a changing
environment, the water drop trajectory changes (12),
(13) formulas were solved numerically by time
discretization, and the obtained values are given in the
graphs in Figure 1.
Figure 1: Change of water droplet flight trajectories in
changing environments.
The graphs are constructed for the state in which
the wind blows in the opposite direction to the water
flow line at 𝜗
= 0 m/s, 𝜗
= 3 m/s, 𝜗
= 5 m/s,
and 𝜗
= 7 m/s. Initial data in calculations: water
drop diameter 𝑑
=2 mm, takeoff angle 25 degrees,
rainfall height h=0.7 m. The initial ϑ
B
= 8 M/S makes
a drop of flying water with a wind speed of 𝜗
= 0
m/s with a takeoff distance of L = 5.1 m (Figure 1a).
As the wind speed increases, the water drop begins to
deform the flight trajectory. At wind speed 𝜗
= 3
m/s, the takeoff distance is equal to L = 3.1 meters.
the takeoff distance at 𝜗
= 5 m/s is L = 1.7 m, at 𝜗
= 7 m/s is L = 0.1 meters. Under the influence of wind
speed, the deformation of the trajectory of the water
drop fly willalso lead to an increase in the distance
Δh. The Δh value increases from Δh=1.2 meters to
Δh=1.3 meters under the influence of wind speed
(Akhmetov et al., 2021; Zhanikulov et al., 2022;
Khudayorov et al., 2023b; Akhmetov et al., 2023;
Sevryugin, 2024; Alimova et al., 2024). Further
increase in wind speed allows the takeoff distance to
have a negative value.
At wind speed 𝜗
= 0 m/s, the drop of water is
evenly distributed over the surface of the field in the
form of an ellipse. With increasing wind speed, a
sharp shift in the distribution along the direction of
the wind is observed.
The calculations made showed that in this case,
the time of the water drop's flight also changes.
Mathematic Modelization of the Absorption of Water Drop by Wind in the Rainbowing Irrigation of Agricultural Crops
173
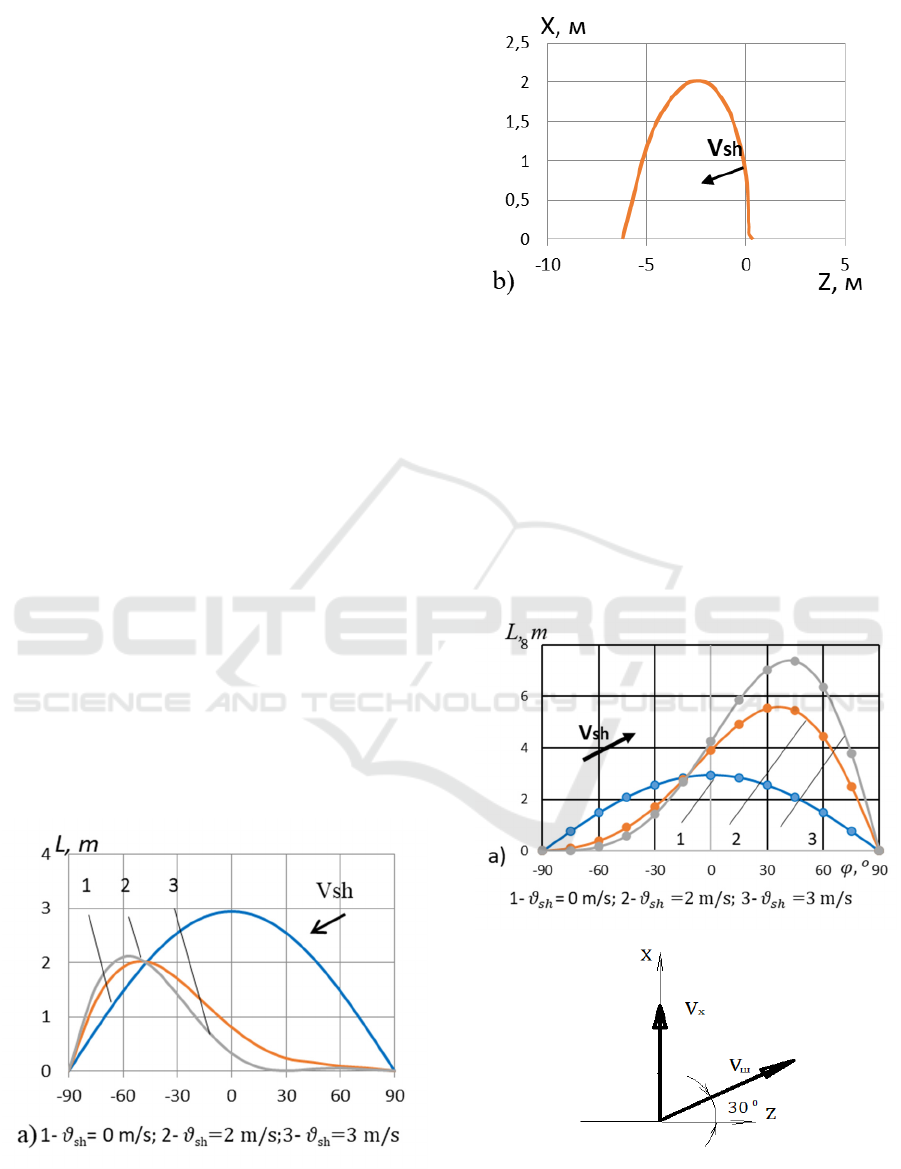
The distribution graph on the field surface of the
flow of water (Figure 2 and Figure 3) was obtained
by projecting the flight distance of a drop of water
flying from the deflector segments onto the XZ axes.
The change in the takeoff distance of a water drop
depends on the value of the changing 𝜗
𝑡- the take
off speed of the drop and 𝜗
-the wind speed, and the
K(t)-the variable coefficient of the environment.
When the wind direction is in the direction of the flow
of water, an increase in the distance of the water drop
and the time of takeoff can be seen.
The graph shows that at 𝜗
= 0 m/s (Figure 3a)
the water drop has a fly distance of L = 2.94 m. When
the wind speed is equal to 𝜗
= 2-3 m/s, the takeoff
distance decreases and l = 1.93-1.99 m, it should be
noted that the greatest values of the water drop speed
belong to the drop of water, which is shot out of
segments located at 45-60o degrees. Under the
influence of wind speed, there is a deformation of the
drop velocity, which is rained from the segments of
the 1st half of the deflector.
The graph in Figure 3b shows the distribution of
the flow of water on the field surface as a result of the
deformed velocity. The graph shows that the
distribution of the water flow is shifted along the Z-
axis and |-6.2;0.2| localizes in the cross section.
The variation in the distance to fly a drop of water
under the influence of the wind blowing in the
direction of water drop is depicted in the graph in
Figure 3. When the wind speed changes in the range
𝜗
= 2-3 m/s, the takeoff distance of the water drop
from the 1st half of the deflector will have a critical
small value. Reaches its maximum value in the 2nd
half of the deflector. Wind speed reaches L = 8 m
when 𝜗
= 3 m/s.
Figure 2: The distribution of the water drop on the field
surface when the wind speed is directed against the water
flow and the effect of the wind speed on the flight distance:
a) the influence of wind speed on the distribution of the
water flow on the field surface; b) the epic of the
distribution of water flow on the field surface.
The graphs in Figure 3b show the Epura of
distribution on the field surface of a drop of water
under the influence of wind blowing at an angle θ=
30º in the direction of rainmaking. Under the
influence of wind, water droplets shift from octant I
to octant II of the XOZ coordinate system.
I-CRAFT 2024 - 4th International Conference on Research of Agricultural and Food Technologies
174
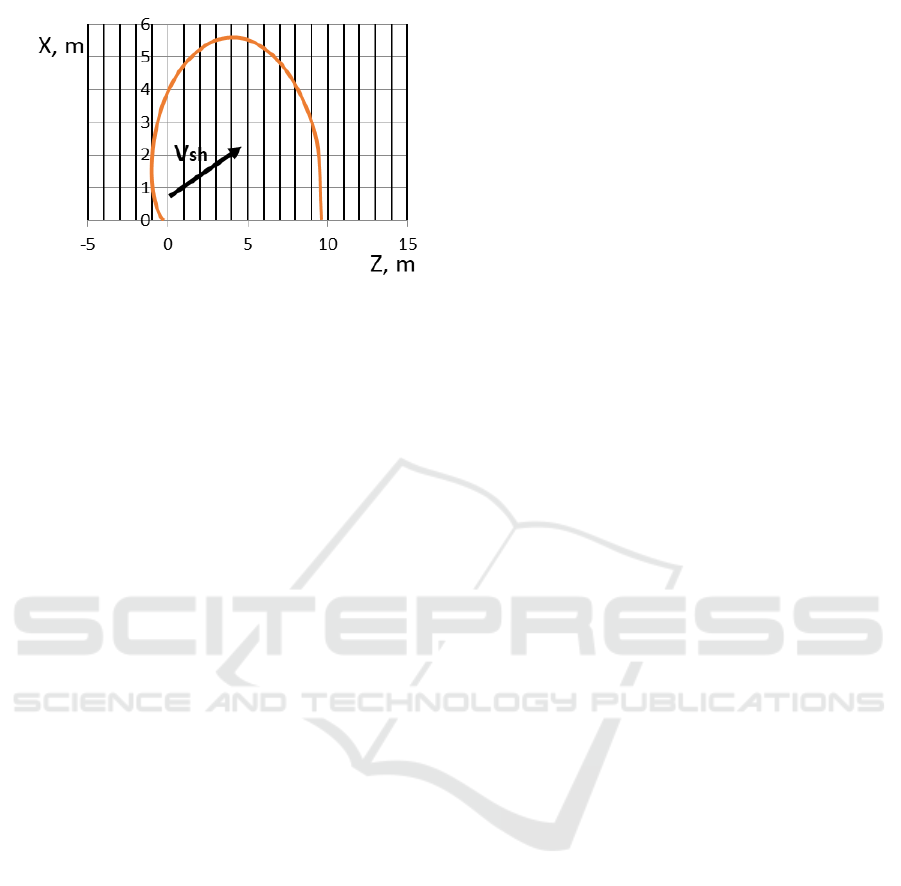
b)
Figure 3: The distribution of the water drop on the field
surface when the wind speed is directed along the water
flow and the effect of the wind speed on the flight distance:
a) the effect of the wind speed on the distribution of the
water flow on the field surface; b) the epic of the
distribution of the water flow on the field surface.
4 CONCLUSIONS
When the initial takeoff speed of the water drop is less
than the wind speed, the takeoff distance of the water
drop will have a negative value. the flight distance of
a drop of rainwater from H = 2.0 meters is reduced
from L = 7.54 meters to L = 4.0 meters under the
influence of wind with a speed of 𝜗
= 7 M/s. The
results obtained indicate that the condition 𝜗
> 𝜗
must be met in order to reduce the blowing of a drop
of water under the influence of the wind.
Taking into account the fact that as a result of the
calculations performed, rain irrigation machines
should carry out effective irrigation under conditions
with a wind speed of up to 7 m/s (ATT), it is
necessary to construct the device to ensure the height
of rainmaking at a value of h = 0.7 m and the initial
flight speed of the water drop at a 𝜗
=7−8 m/s.
REFERENCES
Akhmetov, A.A., Allanazarov, M.A., Muratov, L.B.,
Kambarova, D.U., 2021. Installation of passive
working tools with lancet foot in one row with
overlapping. IOP Conference Series: Earth and
Environmental Science, 868, 012075. DOI:
10.1088/1755-1315/868/1/012075.
Akhmetov, A.A., Akhmedov, Sh.А., Allanazarov, M.A.,
Asamov, R.H., 2023. Ensuring the reliability of
adjusting the clearance of a four-wheel tractor. IOP
Conference Series: Earth and Environmental Science,
1138, 012047. DOI: 10.1088/1755-
1315/1138/1/012047.
Akpasov, A.P., 2018. Improving the efficiency of rain
formation with the justification of the design
parameters of circular deflector nozzles. Dissertation,
Doctor of Technical Sciences. Saratov. p.141.
Alimova, F., Saidova, M., Boboniyozov, E., & Mirzayev,
B., 2024. Analysis of the state of mechanized sowing of
rice in seedlings. BIO Web of Conferences, 85, 01032.
https://doi.org/10.1051/bioconf/20248501032.
Khudayorov, Z., 2024a. Formation of artificial raindrops on
the deflector attachment of rainmaking machines.
British Journal of Global Ecology and Sustainable
Development, 28, 57-62.
https://journalzone.org/index.php/bjgesd/article/view/5
54.
Khudayorov, Z., 2024b. Investigation of the process of
irrigating agricultural lands under artificial irrigation.
World Bulletin of Social Sciences, 34, 36-39.
https://scholarexpress.net/index.php/wbss/article/view/
4172.
Khudayorov, Z., Khalilov, R., Gorlova, I., Mirzakhodjaev,
S., Mambetsheripova, A., 2023a. Mathematical model
of water drop trajectory in artificial rainfall. E3S Web
of Conferences, 365, 04011.
https://doi.org/10.1051/e3sconf/202336504011.
Khudayorov, Z., Khalilov, R., Mirzakhodjaev, S.,
Nurmikhamedov, B., Mamasov, S., 2023b. Theoretical
study of the influence of the changing environment on
the process of rainfall irrigation. E3S Web of
Conferences, 376, 02013.
https://doi.org/10.1051/e3sconf/202337602013.
Khudayorov, Z.X., 2022. Evaporation of a drop of water
when watering rain. "Irrigation and melioration".
Scientific-Practical, Agrarian - Economic Journal,
Special issue.
Mirzakhodjaev, S., Allanazarov, M., Ishmuratov, K., 2024.
Hardening of gear teeth depending on the concentration
of abrasive particles in the transmission oil. BIO Web of
Conferences, 85, 01043.
https://doi.org/10.1051/bioconf/20248501043.
Sevryugin, V.K., 1998. Improvement of irrigation
technique and technology by sprinkling in the
conditions of Central Asia. Dissertation, Doctor of
Technical Sciences. Tashkent.
Vinogradov, A.G., 2015. Calculation of parameters of fire-
fighting jets of sprayed water. Vinogradov, A.G.,
Yakhno, O.M. Practical Hydromechanics, 7(4).
Voronin, V.V., 1988. Interaction of liquid jets with the
atmosphere. Moscow: TsAGI.
Zhanikulov, S., Khalmuradov, T., Allanazarov, M., 2022.
Prerequisites for improving the cleaning process dried
seedless grapes (Sultanas). IOP Conference Series:
Earth and Environmental Science, 1112, 012015 DOI:
10.1088/1755-1315/1112/1/012015.
Zhelyazko, V.I., Lukashevich, V.M., 2015. Methods of
improving the quality of sprinkling when watering with
the BAUER RAINSTAR T-61 machine. Irrigation.
MiVH, No. 3, Minsk.
Mathematic Modelization of the Absorption of Water Drop by Wind in the Rainbowing Irrigation of Agricultural Crops
175
