MATLAB Based Graphical User Interface for Parameter

Computation of Type II and Type III Controllers for DC DC

Converters

Hariharan J

, J Harish Arjun

, Karthik M Rao

, Sohan P

and M. Premkumar

Department of Electrical and Electronics Engineering, Dayananda Sagar College of Engineering,

Kumaraswamy Layout, Bangalore, Karnataka, India

Keywords: DC-DC Converter, GUI, Type II and Type III Controller, MATLAB.

Abstract: A MATLAB-based graphical user interface (GUI) is presented for the optimal design of Type II and Type III

controllers for DC-DC converters, including buck, boost, and buck-boost types. This GUI combines

traditional design methods with computational algorithms, allowing users to automatically calculate and

display the required parameter values for both controller types. It simplifies the design process while, at the

same time making sure that the

converters

operate

with enhanced

stability,

faster

transient

response,

and

reduced

steady-state error. This interface thereby supports optimization under various conditions of

operation, thus facilitating the gap between theoretical analyses and practical implementation, making it

easier for engineers to achieve optimal.

1 INTRODUCTION

This study focuses on the development of an

advanced and user-friendly boundary breaker for both

Type II and Type III controllers in DC -In DC

converters. These converters are essential

components of power management systems in all

modern electronics and require precision to ensure

robustness and efficiency. The design boundary grid

implemented in MATLAB is mainly designed to

allow the calculation of compensator parameters,

thereby simplifying, and simplifying the design

process for engineers and researchers. This paper

aims to improve the stability and performance of DC-

DC converters on different topologies, including

buck, boost and buck-boost configurations. The core

of this paper is to determine a MATLAB-based

design boundary that lets users input specific

parameters for the DC-DC converters.

https://orcid.org/0009-0002-3177-794X

https://orcid.org/0009-0007-8220-083X

https://orcid.org/0009-0005-6113-9449

https://orcid.org/0009-0004-9428-432X

https://orcid.org/0000-0003-1032-4634

Once this information is obtained, the bounding

unit determines compensator parameter values with

traditional methods and computation algorithms both

for Type II and Type III compensators. This

automated process not only speeds up the design

process but reduces the risk of errors, something

which ensures timely and careful planning. The heat

socket further improves the design by generating

various frequency curves for the DC-DC converter,

providing visual insight into the frequency response

of the system and aiding in the analysis of stability

and yield. The primary goal of this paper is to analyze

and optimize stability for DC-DC converters using

type II and type III controllers. By analyzing the

performance of these two types, the paper intends to

identify the optimal conditions under which each

controller and converter makes itself manifest.

The ability to easily switch between Type II and

Type III controllers within the interface gives the

engineers enough flexibility to address various

150

J, H., Harish Arjun, J., M Rao, K., P, S. and Premkumar, M.

MATLAB Based Graphical User Interface for Parameter Computation of Type II and Type III Controllers for DC DC Converters.

DOI: 10.5220/0013652400004639

In Proceedings of the 2nd International Conference on Intelligent and Sustainable Power and Energy Systems (ISPES 2024), pages 150-156

ISBN: 978-989-758-756-6

operational scenarios and performance demands.

Adaptability is actually very important because

different topologies of DC-DC converters and load

conditions necessarily require different control

strategies to acquire optimal performance. In this

regard, the interface allows for a more tailored

approach to design with the incorporation of both

types of controllers; hence, each converter achieves

the highest level of stability and efficiency regardless

of the specifics of the application or environment. The

paper further explores how these controllers impact

the transient and steady-state error of DC-DC

converters. Using careful tuning of compensator

parameters, the interface minimizes such critical

metrics for the performance results in faster response

times and stable operations.

2 LITERATURE REVIEW

The vast literature provides various strategies to

control and optimize DC-DC converters, which

continue to advance in this field. There is one

innovation introduced through a tri- state buck-boost

converter with an optimized Type-3 controller using

Particle Swarm Optimization (PSO), which

effectively removes the RHP zero of conventional

buck- boost converters, providing greatly improved

control-to-output stability and dynamic parameters

and open-loop gain visualization for various

topologies like buck, boost, or buck-boost converters.

The result is a streamlined design for controllers that

ensures better transient and steady-state responses. In

addition, the robustness and flexibility of PID

controllers on DC-DC converters are highlighted. On

voltage-mode buck converters, digital PID controllers

have shown much higher phase margins and better

stability and overall performance with such digital

control elements as ADCs and digital PWM

Another detailed investigation regarding Type-II

and Type- III controllers is that the controllers have

transient responses and also achieve a good steady

state in high-order converters, such as fourth-order

systems. Models like these were tested for the

practical case with the help of MATLAB-Simulink

simulations. The studies on the application of

classical PID controllers to boost converters

emphasize the ability to maintain voltage regulation,

even in the presence of variations due to input and

load conditions, with some minimizing harmonic

distortion, improving power factors, and maximizing

efficiency. However, Type-II controllers provide

easier implementations and satisfactory performance

for certain applications, so there is still scope to carry

out a comparison. Algorithmic developments,

incorporating PSO and hybrid techniques, have been

routinely applied to fine-tune the controller

parameters for best performance, tackling challenges

such as reduced settling time and better dynamic

response. Relative studies also express the need for

controller selection to enhance the reliability of power

conversion systems used in critical applications, such

as renewable energy, power grids, and

telecommunications. This also proved that practical

challenges in achieving consistent control of DC-DC

converters under varying load currents and input

voltage conditions are acknowledged by the research,

especially in industrial applications. Despite these

advances, the integration of generalized interfaces,

unified frameworks, and broader topological

applicability remains limited, indicating a fragmented

research landscape that calls for consolidation.

Reviewing the presented studies reveals

significant results but also some significant gaps.

Present work has been much focused on Type-III

controllers and their application on the different types

of converters while the focus on Type-II controllers

is less. This creates a comparative gap in

understanding applications that could be linked with

this. Most works concentrate on specific converters,

for instance, on a buck or boost and do not present

generalized design interfaces that may accommodate

a broader range of converters, like buck-boost. While

techniques such as PSO and advanced algorithms are

applied for controller tuning in the techniques used

are highly scenario-specific and cannot be

generalized to multiple controllers or different

topologies optimization techniques, and comparative

evaluations of diverse controller types.

3 METHODOLOGY

The methodology in this paper is understood to be an

organized and detailed approach towards the

designing of a Graphical User Interface (GUI) aimed

at the optimization of the design and analysis of the

Type II and Type III controllers for DC-DC

converters. The first stage consisted of meticulous

literature reviews and theoretical analysis to lay down

the understanding from a fundamental point of

control strategies for DC-DC converters, primarily

Type II and Type III compensators. This stage

incorporates a detailed study of mathematical

modelling and transfer functions relevant to various

types of converters, such as buck, boost, and buck-

boost. Ideally, the goal is to create a fundamental

basis for the subsequent stages. Following the

MATLAB Based Graphical User Interface for Parameter Computation of Type II and Type III Controllers for DC DC Converters

151

theoretical foundations, system modelling and

simulation is the next step, where the selected DC-DC

converters are modelled using MATLAB/Simulink.

In the discussion that follows, building small-signal

models and derivation of transfer functions for each

converter type permits an accurate simulation of the

converters' open-loop behavior, thus gaining insight

into their inherent system dynamics. In the controller

design and parameter selection phase, Type II and

Type III compensators are designed based on the

previously derived transfer functions. This involves

employing Bode plot analysis to fine-tune the

compensator parameters—such as gain, poles, and

zeros—to achieve the desired stability and

performance criteria. The goal of this step is to ensure

an adequate transient response and steady-state

performance, enhancing the controller's overall

efficiency and robustness.

3.1 K-Factor Method

K Factor was created primarily to assist in the

determination of amplifier R and C values. This is

defined as the root of the ratio of the pole to the

zero frequency in Type 2 controllers and the ratio

of double pole frequency over double zero

in Type 3 amplifiers. Choose a cross-over frequency,

desired phase margin, determine the required

amplifier gain and calculate the

required phase boost. Calculate the Phase boost using

Eq. 1 (Prokopev et al., 2019).

𝐵𝑜𝑜𝑠𝑡 = 𝑀 − 𝑃 – 90 (1)

Where, M = desired phase margin (degrees) and p =

modulator phase shift (degrees). The mentioned

expressions apply to Type 2 amplifiers only.

𝐾 = 𝑇𝑎𝑛 [(





) + 45]

(2)

converters and not applicable to a wide range of

variations in input-output conditions for scalable

solutions or interfaces. Overall, the research is

fragmented, and there is a need for a unified

framework that integrates generalized interfaces,

𝐶









(3)

𝐶



=𝐶



(𝐾



−1) (4)

𝑅







(5)

𝐾=𝑇







𝑩𝒐𝒐𝒔𝒕





+ 452 (6)

𝐶









(7)

𝐶



=𝐶



(𝐾 − 1) (8)

𝑅



√





(9)

𝑅









(10)

𝐶













(11)

These parametric equations allow the precise

calculation and error analysis of loop performance

without the iterative process normally associated

with stability analysis.

3.2 PSO Algorithm

Particle Swarm Optimization (PSO) is an

evolutionary algorithm that optimizes the continuous

or discrete, linear or nonlinear, constrained or

unconstrained, and non- differentiable functions by

trying iteratively to improve the solutions with

respect to different parameter values (Chan et al.,

2015). The key components of PSO include:

Particles: These are individual candidate solutions

represented as vectors in a multidimensional space,

where each vector corresponds to a set of parameters

(in this case, compensator values R and C).

Position and Velocity: Each particle has a position in

the search space and a velocity that determines how

it moves within that space. The position of the

particle represents a potential solution (e.g., a set of

values for R and C), while the velocity determines

how the particle updates its position in subsequent

iterations.

Best Positions:

Personal best (pBest): Each particle tracks its best

solution found so far in terms of the objective

function.

Global best (gBest): The best solution found by any

particle in the entire swarm.

Update Rules: The position and velocity of each

particle are updated according to the following

equations:

𝑉



()

=𝑊.𝑉



()

+𝐶



𝑟



𝑃



−𝑥



(



)

+

𝐶



𝑟



𝑔



−𝑥



(



)

 (12)

𝑥



()

=𝑥



()

+𝑉



()

(13)

Where: v

(k)

is the velocity of particle i at iteration k,

(k)

is the position of particle i at iteration k, w is the

inertia weight controlling the influence of the

previous velocity, c1 and c2 are acceleration

coefficients that control the attraction to personal and

ISPES 2024 - International Conference on Intelligent and Sustainable Power and Energy Systems

152

global best positions, r1 and r2 are random numbers

between 0 and 1, pBest and gBest are the personal and

global best positions, respectively. The flowchart of

the PSO algorithm is shown in Fig. 1.

Particle Swarm Optimization is one viable

optimization technique to use in fine-tuning the

parameters of control compensators, such as

resistance and capacitance, to optimize system

performance. Because such behavior of particles

finds optimal/near-optimal solutions in the parameter

space within reasonable computational time, it is,

therefore, efficient in search. This places PSO as a

valuable tool in compensator design to optimize

system performance in any application. Then comes

the simulation stage of the paper, wherein the closed-

loop system would be simulated with all the designed

compensators put in place. At this stage, the

performance based on stability, transient response,

and steady-state error is evaluated with iteration of

the tuning of compensator parameters for better

performance. Through this iteration, there is a

refining of the compensator design to meet desired

specifications in real applications. Finally, a

frequency response analysis and visualization are

carried out to understand and interpret the system's

frequency response characteristics. With tools like

Bode plots, the paper visually examines the effects of

variations in parameters on system stability and

performance. This stage helps us understand the

trade-offs available for controller design and how

decisions are made, and modifications are done to

achieve an optimal balance in competing

performance metrics. This approach attempts to

achieve a robust, user-friendly GUI by efficiently

guiding users through the intricate process of

designing and analyzing Type-II and Type-III

controllers for DC- DC converters.

Figure 3.1: Flowchart

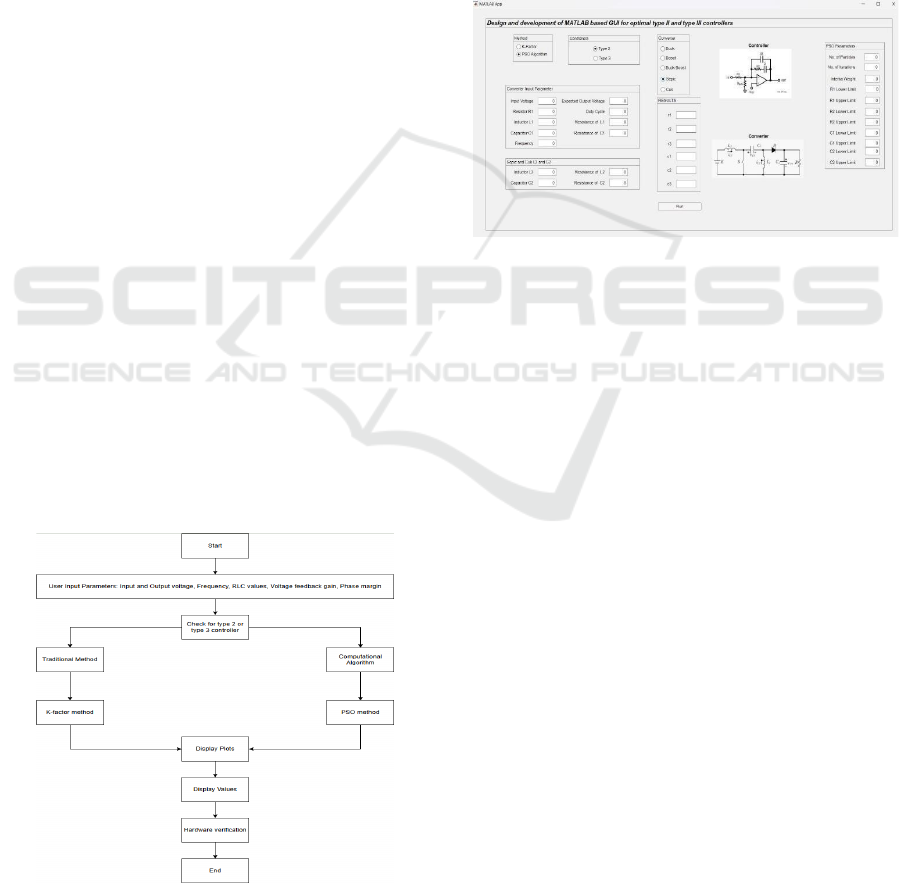
4 RESULTS AND DISCUSSIONS

The proposed method successfully integrates a

MATLAB-based GUI for the design and analysis of

Type II and Type III controllers for DC-DC

converters, as shown in Fig. 2. The GUI is user-

friendly and incorporates robust computational

algorithms to automate the calculation of

compensator parameters such as resistors and

capacitors. These parameters are directly derived

from the transfer functions of various converter

topologies, such as buck, boost, and buck-boost, and

have been seamlessly integrated into MATLAB

Simulink simulations.

Figure 4.1: GUI

Simulation of the closed-loop behavior of DC-DC

converters by the designed compensators provided a

good validation of the system performance. The

interface between the GUI and Simulink provides

real-time visualization and analysis of the system

dynamics, frequency response, and stability margins.

Such analysis tools as Bode plots are very useful in

giving some insight into gain and phase margins and

aid in the fine-tuning of the

parameters of the

compensators to optimal performance. Key results

achieved include:

Automated Parameter Integration: The GUI

successfully calculated and transferred compensator

parameters to MATLAB Simulink, streamlining the

design and simulation process.

Improved Converter Stability: The controllers

designed via the GUI enhanced the stability of the

converters, maintaining steady operation across

varying load and input conditions.

Enhanced Transient Response: Simulations

demonstrated faster response times and reduced

overshoot, ensuring the converters' ability to handle

sudden changes in input or load.

Accurate Frequency Response Visualization: Bode

plots generated through the GUI provided clear

insights into stability metrics and trade-offs, aiding in

MATLAB Based Graphical User Interface for Parameter Computation of Type II and Type III Controllers for DC DC Converters

153

iterative tuning.

Wide Applicability: The GUI's versatility in

supporting multiple converter topologies validates its

effectiveness as a universal tool for power electronics

engineers.

(a)

(b)

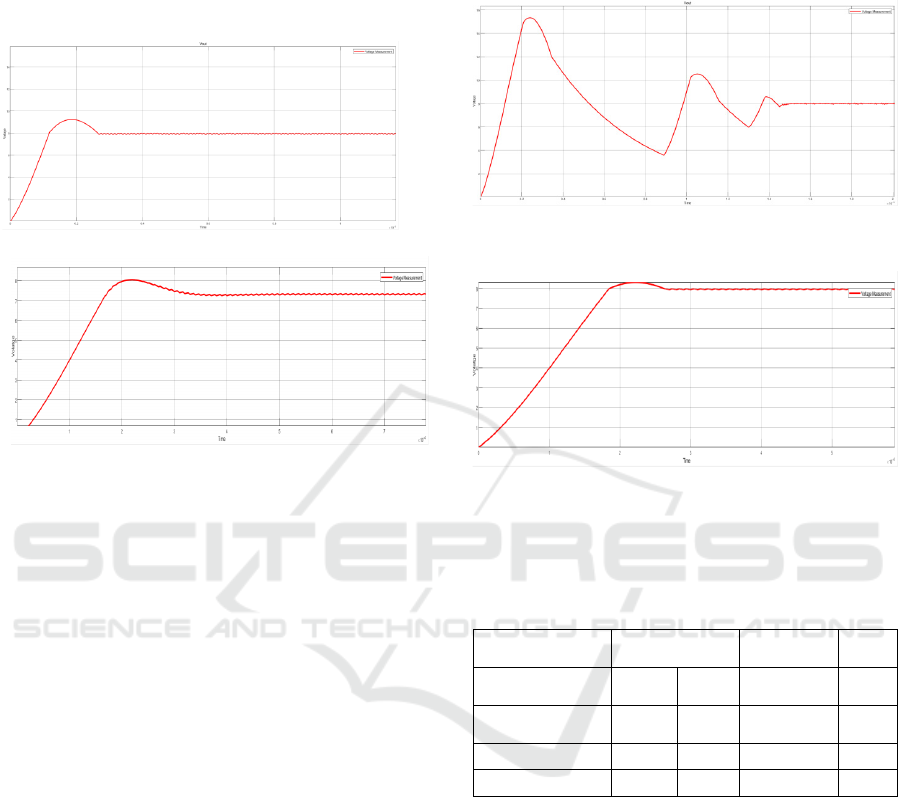
Figure 4.2.1: Output Waveform for Type -2 controller for

Buck Converter; (a) K-factor, (b) PSO

From the values obtained from the GUI, it is observed

that the maximum overshoot is the same for both the

K-factor and PSO methods, but rise time is less in the

PSO method than the K-Factor method and settling

time is less in the K- Factor method than the PSO

method, so it is concluded that and K-Factor and PSO

method is both suitable for getting the required output

for Type-III controller for the buck converter. The

output voltage obtained for the buck converter with

the K-factor method and PSO method is presented in

Fig. 4. The time domain specifications of the buck

converter with Type-II and Type-III controllers are

recorded in Table I.

4.1 Type II and Type III Controller

Analysis for Buck Converter

From the values obtained from the GUI, it is observed

that the maximum overshoot, rise time and settling

time is less in the PSO method than in the K-Factor

method, so it is obvious that the PSO method is more

suitable for getting the required output for Type-II

controller for the buck converter. The output voltage

obtained for the buck converter with the K-factor

method and PSO method is presented in Fig. 3. The

time domain specifications of the buck converter with

Type-II and Type-III controllers are recorded in Table

(a)

(b)

Figure 4.2.2: Output Waveform for Type -3controller for

Buck Converter; (a) K-factor, (b) PSO

Table 1: Time Domain Specifications values for Buck

converter with controllers

Buck (Type-II) Buck (Type-

III)

Specifications K-

Factor

PSO K-Factor PSO

Maximum

Overshoot

15.0% 14.6% 87.5% 87.5%

Rise Time (s) 0.00118 0.00117 0.00118 0.00117

Settling Time (s) 0.00265 0.00261 0.00146 0.00196

4.2 Type II and Type III Controller

Analysis for Boostconverter

From the values obtained from the GUI, it is observed

that the maximum overshoot is less in the K-Factor

method than the PSO method, but rise time is less in

the K-Factor method than the PSO method and

settling time is less in the PSO method than the K-

Factor method, so it is concluded that K-Factor

method is more suitable for getting the required

output for Type-II controller for boost converter.

The output voltage obtained for the buck converter

with the K-factor method and PSO method is

presented in Fig. 5. The time domain specifications of

ISPES 2024 - International Conference on Intelligent and Sustainable Power and Energy Systems

154

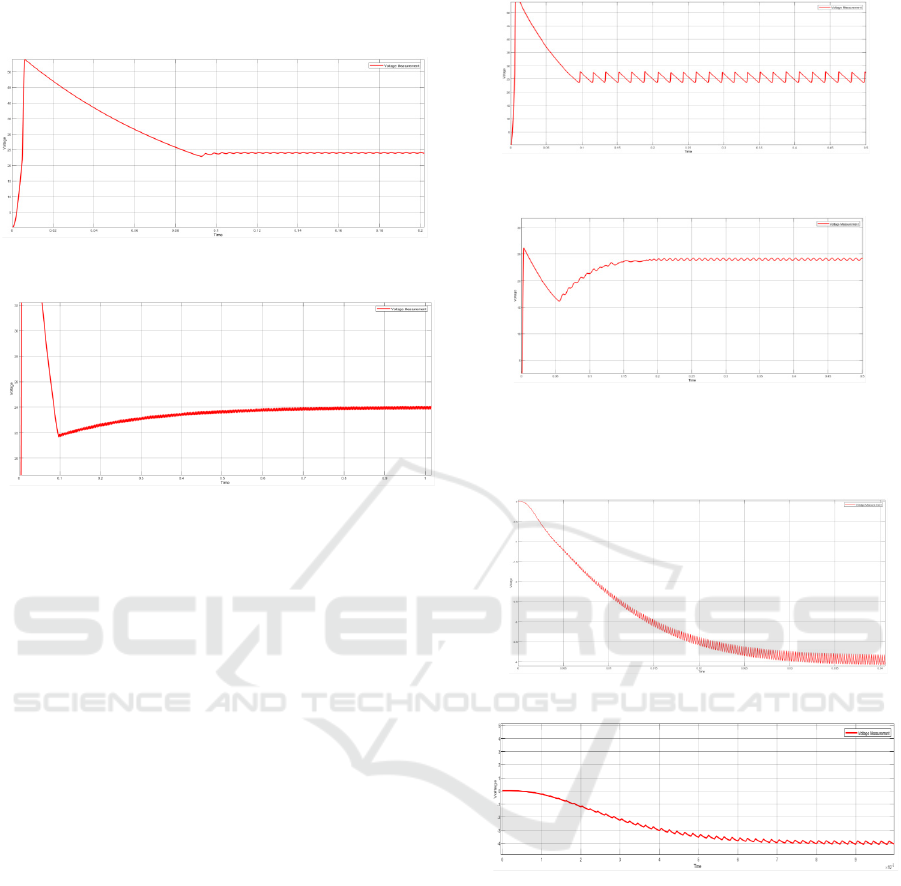
the boost converter with Type-II and Type-III

controllers are recorded in Table II.

(a)

(b)

Figure 4.2.3: Output Waveform for Type-II controller for

Boost Converter; (a) K-factor, (b) PSO

From the values obtained from the GUI, it is observed

that the maximum overshoot is less in the K-Factor

method than the PSO method, but the rise time is the

same in the K- Factor method and the PSO method

and settling time is less in the K-Factor method than

the PSO method, so it sic concluded that K-Factor

method is more suitable for getting the required output

for Type-II controller for boost converter. The output

voltage obtained for the buck converter with the K-

factor method and PSO method is presented in Fig. 6.

The time domain specifications of the boost converter

with Type-II and Type-III controllers are recorded in

Table II.

(a)

(b)

Figure 4.2.4: Output Waveform for Type-III controller for

Boost Converter; (a) K-factor, (b) PSO

(a)

(b)

Figure 4.2.5: Output Waveform for Type-II controller for

Buck- Boost Converter; (a) K-factor, (b) PSO

From the values obtained from the GUI, it is

observed that the maximum overshoot, rise time and

settling time are less in the K-Factor method than in

the PSO method, so it is concluded that K-Factor is

more suitable for getting the required output for

Type-III controller for the buck-boost converter. The

output voltage obtained for the buck converter with

the K-factor method and PSO method is presented in

Fig. 8. The time domain specifications of the buck-

boost converter with Type-II and Type-III controllers

are recorded in Table III

MATLAB Based Graphical User Interface for Parameter Computation of Type II and Type III Controllers for DC DC Converters

155

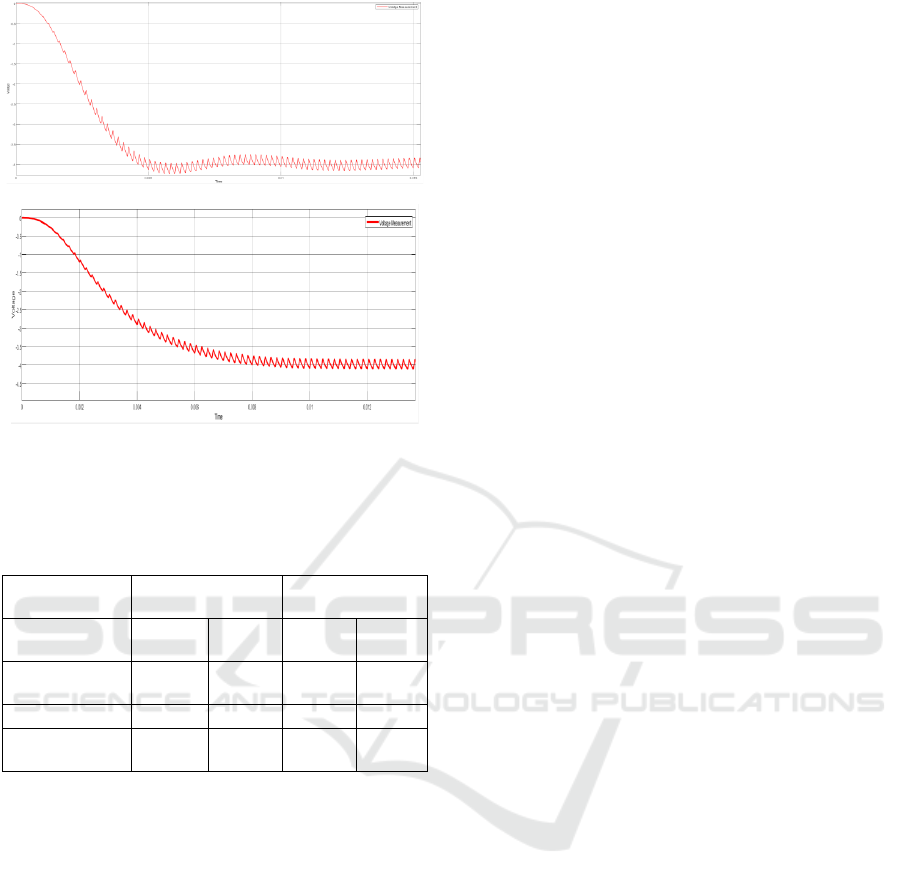
(a)

(b)

Figure 4.2.6: Output Waveform for Type-III controller for

Buck-Boost Converter; (a) K-factor, (b) PSO

Table 3: Time Domain Specifications for Buck-Boost

converter with controllers

Buc

-Boost

ype

-II)

Buc

-Boost

ype

-III)

Specifications

Factor

PSO

Factor

PSO

Maximum

Overshoot

7.5% 5.0% 5.0% 12.5%

Rise Time (s) 0.03000 0.01640 0.00460 0.01760

Settlin

Time

(s)

0.04020 0.02482 0.01842 0.02220

5 CONCLUSIONS

By presenting MATLAB-based GUI, the design of

Type II and Type III controllers for DC-DC

converters can easily be performed, in the sense that

engineers can obtain optimized converter

performance in terms of improved stability, faster

transient response and lower steady-state error. The

interface integrates computational algorithms with

traditional design techniques to increase precision

and efficiency in parameter selection for a wide range

of converter types such as buck, boost, and buck-

boost. The dual controller characteristic of GUI

enables greater performance over a broad range of

operating conditions between theoretical models and

practical realization.

The GUI can be extended for a future scope with

other converter types, such as Cuk or SEPIC

converters and other control strategies such as

predictive or adaptive control. Its utility could further

be expanded with integration to real- time hardware

in the loop testing and machine learning algorithms

for automated optimization. In addition, the web-

based interface would increase accessibility and

usability to the broader engineering audience.

REFERENCES

Andrey Prokopev, Zhasurbek Nabizhanov, Vladimir

Ivanchura, & Rurik Emelyanov. (2019). Design of

Controllers for Higher Order Systems. 2019

International Multi-Conference on Engineering,

Computer and Information Sciences (SIBIRCON),

0607–0611.

https://doi.org/10.1109/sibircon48586.2019.8958442

Chan, N. K.-F., Lam, N. C.-S., Zeng, N. W.-L., Zheng, N.

W.-M., Sin, N. S.-W., & Wong, N.

M.-C. (2015). Generalized Type III controller design

interface for DC-DC converters. 1–6.

https://doi.org/10.1109/tencon.2015.7373052

De, K., Mohanty, S., & Prasad, M. (2019). Modelling,

Design and Control of a Step-Up Chopper Using PID

Controller. International Journal of Research and

Innovation in Applied Science (IJRIAS) |, IV, 2454–

6194.

https://www.rsisinternational.org/journals/ijrias/Digita

lLibr ary/Vol.4&Issue1/18-23.pdf

Mirza Fuad Adnan, Mohammad Abdul Moin Oninda,

Mirza Muntasir Nishat, & Nafiul Islam. (2017). Design

and Simulation of a DC - DC Boost Converter with PID

Controller for Enhanced Performance. International

Journal of Engineering Research And, V6(09).

https://doi.org/10.17577/ijertv6is090029

Muhammad Khamim Asy'ari, & Musyafa, A. (2018).

Design of Buck Converter Based on Interval Type-2

Fuzzy Logic Controller. 5, 153–156.

https://doi.org/10.1109/isitia.2018.8711236

Rana, N., Ghosh, A., & Banerjee, S. (2018). Development

of an Improved Tristate Buck–Boost Converter With

Optimized Type-3 Controller. IEEE Journal of

Emerging and Selected Topics in Power Electronics,

6(1), 400–415.

https://doi.org/10.1109/jestpe.2017.2724847

S Saurav, & Ghosh, A. (2021). Design and Analysis of PID,

Type II and Type III controllers for Fourth Order Boost

Converter. 323–328.

https://doi.org/10.1109/icees51510.2021.9383687

Tiwari, N., & Tiwari, A. N. (2018). Performance Analysis

of Unidirectional and Bidirectional Buck-Boost

Converter Using PID Controller. 1–6.

https://doi.org/10.1109/iementech.2018.8465229

Wang, C.-Y., Ou, Y.-C., Wu, C.-F., & Muh-Tian Shiue.

(2015). A voltage-mode DC-DC buck converter with

digital PID controller. 2322–2326.

https://doi.org/10.1109/fskd.2015.7382315

ISPES 2024 - International Conference on Intelligent and Sustainable Power and Energy Systems

156