
Research on Cooperative Task Assignment of Multi-Agent Track
Bolt Operation Robot Based on Optimized Multi-Objective Particle
Swarm Optimization
Yanni Shen
1
a
, Jianjun Meng
1,2,3,4,*
b
, Defang Lv
1
c
, Gaoyang Meng
1
d
and Zhicheng Wang
1
e
1
School of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China
2
Institute of Mechanical and Electrical Technology, Lanzhou Jiaotong University, Lanzhou 730070, China
3
Gansu Engineering Technology Research Center of Logistics and Transportation Equipment Informatization,
Lanzhou 730070, China
4
Gansu Logistics and Transportation Equipment Industry Technology Center, Lanzhou 730070, China
*
Keywords: Multi-Agent, Track Bolt, Unmanned Vehicles, Task Assignment, Cooperative Control.
Abstract: To improve the efficiency of single-person, single-machine track bolt maintenance during railway skylight
periods, we propose a collaborative task assignment control method using a multi-agent track bolt operation
robot. A control decision model is developed with constraints on operation time and distance, aiming to
optimize both total collaborative operation distance and completion time. By incorporating equations for
robot speed and operation time, we derive the Pareto solution set for multi-agent task assignment. The
method’s effectiveness is verified through an enhanced particle evolution technique within the multi-
objective particle swarm optimization (MOPSO) algorithm, and its performance is compared with that of
standard MOPSO. Simulations in a real-world track bolt maintenance environment show that this approach
produces a higher-quality Pareto solution set for task assignment.
1 INTRODUCTION
As railway construction in China accelerates, daily
track maintenance has become increasingly essential.
The condition of track bolts, a critical component of
the track structure, directly impacts train safety and
stability. However, the current single-person
maintenance method during skylight periods is labor-
intensive, inefficient, and poses safety risks. Thus,
developing an efficient Multi-Agent Track Bolt
Operation Robot (MATBOR) is imperative. In
alignment with the "Digital Railway Planning"
initiative by China National Railway Group Co., Ltd.,
we aim to achieve comprehensive digitalization and
intelligence in railway operations, thereby enhancing
modernization efforts. Improving intelligent maintenance
equipment for track bolts is crucial.
a
https://orcid.org/0009-0006-7316-3806
b
https://orcid.org/0000-0001-6856-2577
c
https://orcid.org/0009-0004-6779-2521
d
https://orcid.org/0000-0002-2973-7976
e
https://orcid.org/0009-0008-1531-9547
This article addresses the collaborative task
assignment problem for Multi-Agent Track Bolt
Operation Robots (MATBOR), a typical NP-hard
challenge marked by high computational complexity
and long processing times (Li et al., 2022).
The Particle Swarm Optimization (PSO)
algorithm is recognized for its high efficiency,
simplicity, and quick convergence, making it ideal for
solving single-objective optimization problems.
However, it is not naturally suited for multi-objective
optimization. Consequently, improving PSO for
multi-objective tasks has become a significant
research focus. Many researchers have extended the
original algorithm and implemented various
improvements to enhance the performance of the
Multi-Objective Particle Swarm Optimization
(MOPSO) algorithm (Figueiredo et al., 2016; Lv et
al., 2016; Zhou et al., 2022; Sunet al., 2024; Wang and
248
Shen, Y., Meng, J., Lv, D., Meng, G., Wang and Z.
Research on Cooperative Task Assignment of Multi-Agent Track Bolt Operation Robot Based on Optimized Multi-Objective Particle Swarm Optimization.
DOI: 10.5220/0013632100004671
In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 248-256
ISBN: 978-989-758-764-1; ISSN: 3051-701X
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)

Liu, 2016; Khan et al., 2016; Wang et al., 2021).
For instance, Liu et al. proposed a co-evolutionary
PSO algorithm that employs synthetic immune
principles, dividing the population into elite and
ordinary subpopulations, which co-evolve for
improved convergence and global search abilities
(Liu et al., 2013). Goh et al. introduced a
collaborative evolution paradigm that combines
competition and cooperation to simultaneously tackle
static and dynamic multi-objective problems (Goh
and Tan, 2009). Song et al. developed a collaborative
evolutionary PSO algorithm based on a bottleneck
objective instructional strategy, maintaining diversity
through distributed collaboration across multiple
populations (Song et al., 2020). Huang et al. proposed
a dual-phase multi-task allocation approach utilizing
Discrete Particle Swarm Optimization (TMA-DPSO),
which iteratively updates particle positions and
velocities to enhance solutions (Huang et al., 2022).
Lastly, Li et al. proposed a gBest strategy, utilizing a
newly defined virtual generation distance index, to
enhance search efficiency (Li et al., 2023).
Building on this foundation, This study introduces
a method for task assignment in MATBOR, utilizing
an optimized MOPSO algorithm. The key
innovations of this study include:
(1) A two-stage subsampling method is
implemented to improve the algorithm's convergence
speed and accuracy.
(2) To address issues such as high computational
complexity, limited diversity in Pareto optimal
solutions, and challenges in handling complex
constraints, this study employs a simple adaptive grid
method to optimize the multi-objective particle
swarm optimization algorithm, thereby enhancing its
efficiency.
(3) Applying a collaborative task assignment
method to MATBOR to enhance maintenance
efficiency during railway skylight periods.
2 METHODOLOGY
2.1 Collaborative Task Assignment
Model for Multi-Agent Rail Bolt
Operation Robot
2.1.1 Problem Description
The collaborative task assignment problem for a
multi-agent rail bolt operation robot system can be
described as follows: assuming there are m
MATBORs operating during a specific skylight
period, represented by the robot set
1234
{, , , , , }
m
Rrrrr r= . if the range of the rail bolt
area to be serviced does not exceed
max
L and n bolts
need to be maintained, the task set T can be
represented as
1234
{, , , , , }
n
Ttttt t= . Here,
i
r
represents the task assignment for the ith robot,
[1, ]im∈
;
j
t
represents the jth task to be assigned,
[1, ]
j
n∈
. The working time during the skylight
period must not exceed
max
T . As shown in Figure 1,
the central control center sends the specific areas and
kilometers that require maintenance to the signal
receiving station, which then relays these
requirements to the monitoring operation screen used
by the maintenance personnel and the MATBORs
during the window period. Once the MATBORs
begin working, they transmit the status of each
completed task and equipment information to the
signal receiving station in real-time. The maintenance
work during the skylight period is considered
successfully completed when all MATBORs have
finished their assigned tasks simultaneously.
Figure 1: Schematic Diagram of Task Assignment for
MATBOR.
2.1.2 Constraints
The MATBOR collaborative task assign-ment model
includes the following key constraints:
(1) Task Coordination Constraints
To ensure that no task is executed multiple times
or left unexecuted, task coordination constraints are
incorporated into the model. This requires that each
task must be executed exactly once and can only be
assigned to a sing-le robot, as expressed in equation
(1).
1
1
n
ij
i
x
=
=
j
T∀∈
(1)
ij
x
represents the assignment of tasks; n
represents total number of tasks.
Research on Cooperative Task Assignment of Multi-Agent Track Bolt Operation Robot Based on Optimized Multi-Objective Particle
Swarm Optimization
249

(2) Robot Coordination Constraints
To prevent errors in task execution, the model
includes constraints for robot coordination. These
constraints guarantee that each robot can undertake
only one task at a t-ime during the assignment process,
as illustrated in equation (2).
1
1
m
ij
j
x
=
=
iR∀∈
(2)
m represents total number of multi-agent systems.
(3) Task Status
The variable representing whether the task
j
t
is
assigned to the robot
i
r is defined as follows: if the
task is assigned to the robot, then:
1
ij
x =
; if the task
is not assigned to the robot, then:
0
ij
x =
. As shown
in equation (3).
{0,1}
ij
x ∈
iR∀∈
,
j
T∀∈
(3)
(4) Homework
All robots begin from the same starting point, and
the bolts are sequentially numbered 1, 2, 3... n starting
fro-m that origin.
(5) Operation Time and Distance Constraints
Given the time and distance limitations for
maintenance work during the skylight period, the
assigned MATBOR must not exceed the specified
time, and the total distance traveled by a single robot
must remain within the maximum allowable distance.
These constraints are express-ed in equations (4) and
(5).
1
m
imax
i
TT
=
≤
(4)
imax
DL≤ (5)
Were:
()
()
()
1
1
ES
S
ij ij
ij
ijij
sw
NN
N
Ttx
vv
−+⋅Δ
+⋅Δ
=+
,
1
ij
n
irtij
j
D
PPx
=
=−⋅
Where,
i
T
represents robot
i
r
completes task
assignment and running time;
i
D
represents robot
i
r
total travel distance;
max
T
represents robot
i
r
maximum running time;
max
L
represents robot
i
r
maximum driving distance;
S
ij
N
and
E
ij
N
represent
complete the starting and ending bolt numbers of the
task separately;
s
V
represents ground speed:
2/
s
Vms=
;
w
V
represents operating speed:
0.45 /
w
Vms=
;
j
t
represents task j execution time;
i
r
P
represents initial position:
(, )
iii
rrr
P
xy=
;
j
t
P
represents task element coordinates:
(, )
jjj
ttt
P
xy=
.
2.1.3 Objective Function
To more effectively evaluate the task assignment
results for the rail bolt robot, this model uses two
objective functions: MATBOR task duration and
overall travel distance.
Task completion time refers to the duration
required to complete the final task in the maintenance
process, while total travel distance refers to the sum
of all distances traveled by the track bolt robots
during the skylight period. The corresponding
calculation formulas are given in equations (6) and
(7).
1
m
1i
i
FmaxT
=
=
(6)
2
1
m
i
i
FD
=
=
(7)
In equations (6) and (7),
1
F
indicates the total
time needed to finish the final task in the complete
maintenance process, which corresponds to the
maximum task completion time.
2
F
represents the
sum of the travel distances of all participating rail bolt
robots across all systems. Since the goal is for the rail
bolt robots to complete tasks as quickly as possible
while minimizing resource consumption during task
assignment, the model put forward in this paper
considers both optimization objectives: minimizing
1
F
and
2
F
simultaneously. Based on these two
objectives, the optimal objective function for
MATBOR collaborative task assignment is
formulated in equation (8).
1
[, ]
2
zminFF= (8)
The MATBOR collaborative task assignment
model involves both discrete and continuous
variables, which complicates the solution space and
makes it more difficult to search effectively.
Additionally, the model includes multiple complex
constraints, such as inequality and equality
constraints, further increasing the irregularity of the
solution space and the difficulty in finding feasible
solutions. To tackle the challenges of multi-objective
and multi-constraint collaborative task assignment in
MATBOR, this paper introduces MOPSO algorithm
that incorporates a quadratic sampling adaptive grid
to address the multi-MATBOR collaborative task
assignment challenge.
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
250

2.2 Multi-Objective PSO Based on
Quadratic Sampling Adaptive Grid
2.2.1 Pareto Optimal Solution
Given the multiplicity and complexity of different
objective functions, it is usually impossible for all
objectives to reach their maximum or minimum
values simultaneously. As a result, multi-objective
optimization problems rarely have a single optimal
solution. However, practical problems require
decision-making to identify the best possible solution.
To address this, Pareto optimal solutions are utilized
to assess and balance conflicting objectives.
In multi-objective optimization, several
objectives are optimized simultaneously. A solution is
considered Pareto optimal if no objective can be
enhanced without negatively impacting another (Lu
et al., 2024). For two decision vectors
x
and
y
,if
x
dominates
y
, denoted as
x
y
, this means that
x
is no worse than
y
in all objectives, and
enhanced in at least one objective.
A decision vector
x
is considered a Pareto
optimal solution if no other vector in the objective
space can dominate it. The group of all these solutions
constitutes the Pareto optimal set (PS), while its
graphical depiction is referred to as the Pareto optimal
frontier (PF). According to the definition, enhancing
one objective in a Pareto optimal solution necessarily
diminishes at least one other. In multi-objective
optimization, this collection is commonly known as
the non-dominated solution set. The algorithm
proposed in this paper aims to identify the Pareto
optimal solution set, thereby enhancing the efficiency
and balance of MATBOR task assignment.
2.2.2 Secondary Sampling
The more particle samples selected in the state space,
the higher the approximation accuracy becomes (Liu,
2017). To address the issue where the weights of
certain particles may reduce the effective sample
space after multiple iterations, thereby affecting
estimation accuracy, the quadratic sampling method
has been introduced (Douc and Cappe, 2005). During
the resampling process, particles with higher weights
are duplicated, while those with lower weights are
discarded, ensuring the particle count remains
constant. Various subsampling methods exis (Li et al.,
2015).
2.2.3 Improved Multi-Objective Particle
Swarm Optimization Algorithm
The PSO algorithm, developed by Kennedy and
Eberhart in 1995, is a swarm intelligence technique
modeled after birds' food-searching behavior. It is
especially adept at addressing complex, nonlinear
continuous optimization challenges (Kennedy and
Eberhart, 1995). Over time, PSO has been enhanced
and adapted to tackle discrete problems as well. These
improvements have expanded its applicability,
enabling it to effectively address NP-hard problems,
combinatorial optimization, and multi-objective
optimization challenges, while also incorporating
global guidance techniques (Yan et al., 2015; Gao et
al., 2023; Lu et al., 2023). In PSO, particles adjust
their direction and velocity for the next iteration by
considering both their individual flight history and
shared information from the swarm, demonstrating
collective intelligence. The particle update equations
are provided in (9) and (10).
11 2 2
( 1) () ( () ()) ( () ())
iiii i
vt vt crpt xt cr gt xt
ω
+= + − + −
(9)
(1) (1) (1)
iii
xt xt vt+= ++ + (10)
Equation (9) represents the velocity update
formula, while equation(10) is the position update
formula. In these equations:
(1)
i
vt+ is the new
velocity of particle i at time t+1;
()
i
vt is the velocity
of particle i at time t;
ω
is the inertia weight, which
controls the influence of the particle's previous
velocity on its current velocity;
1
c and
2
c are
acceleration constants, representing the weights of
individual cognition and group cognition,
respectively;
1
r and
2
r are random numbers in the
range [0,1], used to maintain randomness;
()
g
t i s
the global best position, representing the optimal
position found by the entire particle swarm;
()
i
x
t is
the current position of particle i at time t and
(1)
i
xt+
is the new position of particle i at time t+1.
This paper introduces a two-stage subsampling
method to address the challenges of low solution
accuracy and slow search speed during the middle
and later phases of the PSO algorithm. In the first
stage, particles are sampled from the search space,
where those farther from the non-dominated solutions
are discarded, and those closer are retained and
replicated, enhancing convergence speed and
accuracy. However, this may reduce particle diversity.
To counter this, the second-stage sampling focuses on
non-dominated particles, discarding high-density
particles and replicating low-density ones to preserve
diversity. Since the grid is updated only when extreme
Research on Cooperative Task Assignment of Multi-Agent Track Bolt Operation Robot Based on Optimized Multi-Objective Particle
Swarm Optimization
251
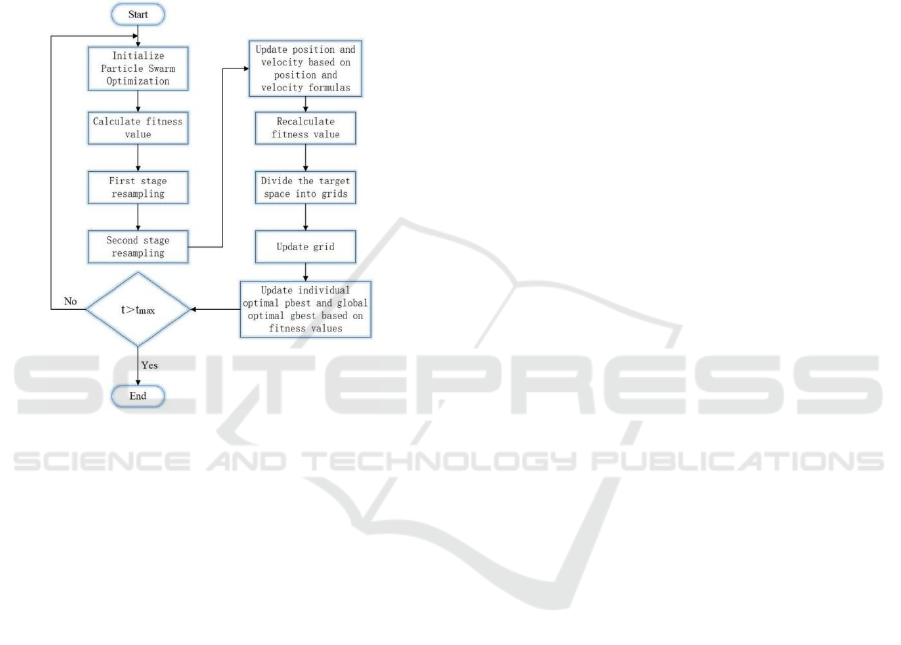
boundary particles appear in the storage set, the mesh
size can sometimes grow too large during evolution,
affecting performance. In the second stage, the target
area is segmented into smaller regions via a grid, and
particle density in each region is used for estimation.
The grid size is adjusted adaptively based on particle
evolution. This leads to the development of MOPSO
algorithm that incorporates quadratic sampling and an
adaptive grid (QSAGMOPSO), as depicted in the
flowchart in Figure 2.
Figure 2: Flowchart of the Algorithm.
Step 1: Initialize the particle position data by
dividing each dimension evenly, using these divisions
as the initial coordinates in the decision space. To
expand the distribution range, each dimension is
divided according to its value range.
Step 2: Utilize the layered sampling method for
secondary sampling. In the first stage, particles with
higher weights are duplicated, while those with lower
weights are discarded, maintaining a constant number
of particles throughout the resampling process.
Step 3: Apply the secondary sampling method
using a layered approach. In the initial stage, particles
with greater weights are duplicated, while those with
lesser weights are removed. The overall number of
particles stays constant during the resampling process.
Step 4: Non-dominated solutions that meet the
criteria are stored in an external file. When the file
reaches its maximum capacity, new qualifying
particles are added by screening the existing ones,
ensuring the particle count remains constant.
Step 5: Determine the Pareto optimal solution set
by assessing the fitness value of each particle for
every objective. Analyze the dominance relationships
between the particles, and collect all non-dominated
solutions to form the current Pareto optimal set.
Step 6: Update each particle's velocity and
position by applying the corresponding update
formulas.
Step 7: Input the particle coordinates into each
objective function and compute the corresponding
function values.
Step 8: Utilize the adaptive grid method to
compute the density of each particle in the Pareto
optimal solution set. The search space is divided into
smaller regions, with higher particle density
indicating a greater number of particles within a grid.
Low-density particles are replicated to preserve
diversity.
Step 9: Using the historical data of each particle,
identify the personal best particle (pbest) and the
global best particle (gbest) based on their past fitness
levels.
3 RESULTS
3.1 Experimental Comparison
To assess the feasibility and effectiveness of the
QSAGMOPSO algorithm, benchmark problems
ZDT1, ZDT2, and ZDT3 were selected for testing,
with the details provided in Table 1. The population
size was set to 400, with 200 generations of iterations
and a file set size of 200. Each test was run 20 times,
as shown in Figure 3. In the figure, red dots represent
the true Pareto frontier, while green dots indicate the
Pareto frontier identified by the QSAGMOPSO
algorithm. A summary of the comparison results,
including the mean and standard deviation for the
ZDT functions, is provided in Table 1.
In the Table 1, variable range:
01
i
x≤≤
,
1, 2, 3, ,im=
,
30m =
.
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
252
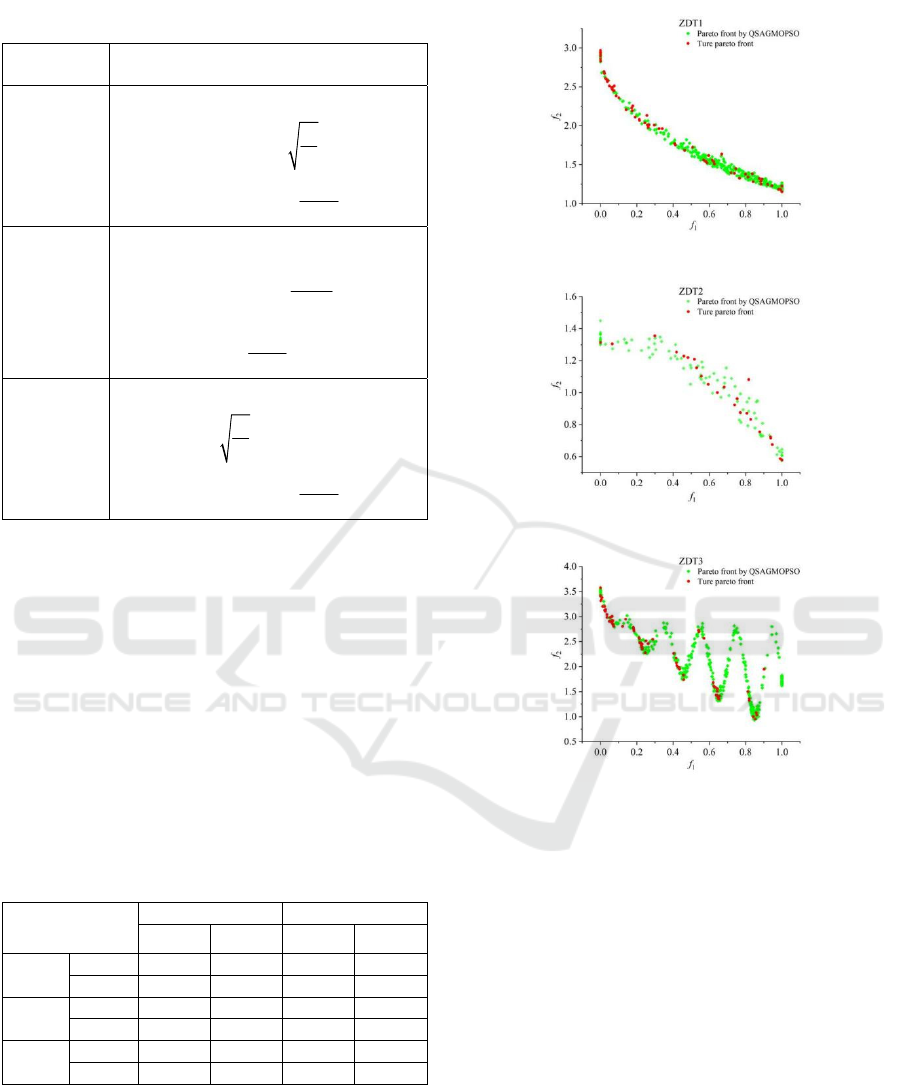
Table 1: Benchmark Test Table.
Test
q
uestions
Objective Function
ZDT1
11
f
x=
1
2
1
f
fg
g
=−
2
19
1
m
i
i
x
g
m
=
=+
−
ZDT2
11
f
x=
()
()
()
2
1
2
1
fx
fgx
gx
=−
2
9
1
1
m
i
i
g
x
m
=
=+
−
ZDT3
11
f
x=
()
1
211
1/sin10
f
f
gfgf
g
π
=− −
2
19
1
m
i
i
x
g
m
=
=+
−
As shown in Table 2, while various indicators can
be used to assess two Pareto frontiers, no single
measure is completely reliable. To address this, the
paper employs two additional quality indicators,
H
I
and
I
∈+
, to compare algorithm performance. These
indicators evaluate how closely the solutions align
with the true Pareto front. Both
H
I
and
I
∈+
, range
from 0 to 1, where higher
H
I
(or lower
I
∈+
) values
indicate a better alignment with the true Pareto front.
The results suggest that the proposed QSAGMOPSO
algorithm outperforms the MOPSO algorithm.
Table 2: Performance Comparison Results of MOPSO and
QSAGMOPSO on Benchmark Functions.
Problem MOPSO QSAGMOPSO
H
I
I
∈+
H
I
I
∈+
ZDT1 Mean 0.8907 0.1564 0.9093 0.1471
Std. 0.0971 0.2790 0.0400 0.1806
ZDT2 Mean 0.6683 0.6500 0.8694 0.4520
Std. 0.4927 0.2472 0.2668 0.2286
ZDT3 Mean 0.7420 0.3695 0.8122 0.1222
Std. 0.8101 0.4553 0.8534 0.1813
a
b
c
Figure 3: Pareto front of ZDT1, ZDT2, ZDT3.
3.2 Task Assignment Coding
Since the particle swarm optimization algorithm uses
real number encoding, it cannot be directly applied to
the discrete task assignment problem in MATBOR.
Therefore, this paper adopts a method of truncating
decimal places and retaining integer digits to decode
the results obtained by the algorithm, effectively
transforming the problem from a continuous domain
into a discrete one. Assuming there are m rail bolt
robots that need to perform n tasks during the skylight
period, the assignment plan is expressed as an n-bit
array
123
[, , , , ]
n
tt t t . Each
j
t
in the array is a
randomly generated number falling within the range
[1, ]m
,and the integer part of
j
t
represents the id of
the robot assigned to perform the jth task. Tasks with
Research on Cooperative Task Assignment of Multi-Agent Track Bolt Operation Robot Based on Optimized Multi-Objective Particle
Swarm Optimization
253
the same integer part are executed by the same rail
bolt robot, while the decimal part is rounded during
the encoding process.
For example, if there are three track bolt robots
tasked with performing 300 jobs during the skylight
period, the task assignment code arrangement is
shown in Table 3.
Table 3: Example of Task Assignment Scheme.
Particle numbe
r
1
66 67
230 231
300
Robot codin
g
3 2 1
In this task assignment scheme, bolts numbered 1
to 66 are executed by Robot 3, bolts numbered 67 to
230 are handled by Robot 2, and bolts numbered 231
to 300 are assigned to Robot 1.
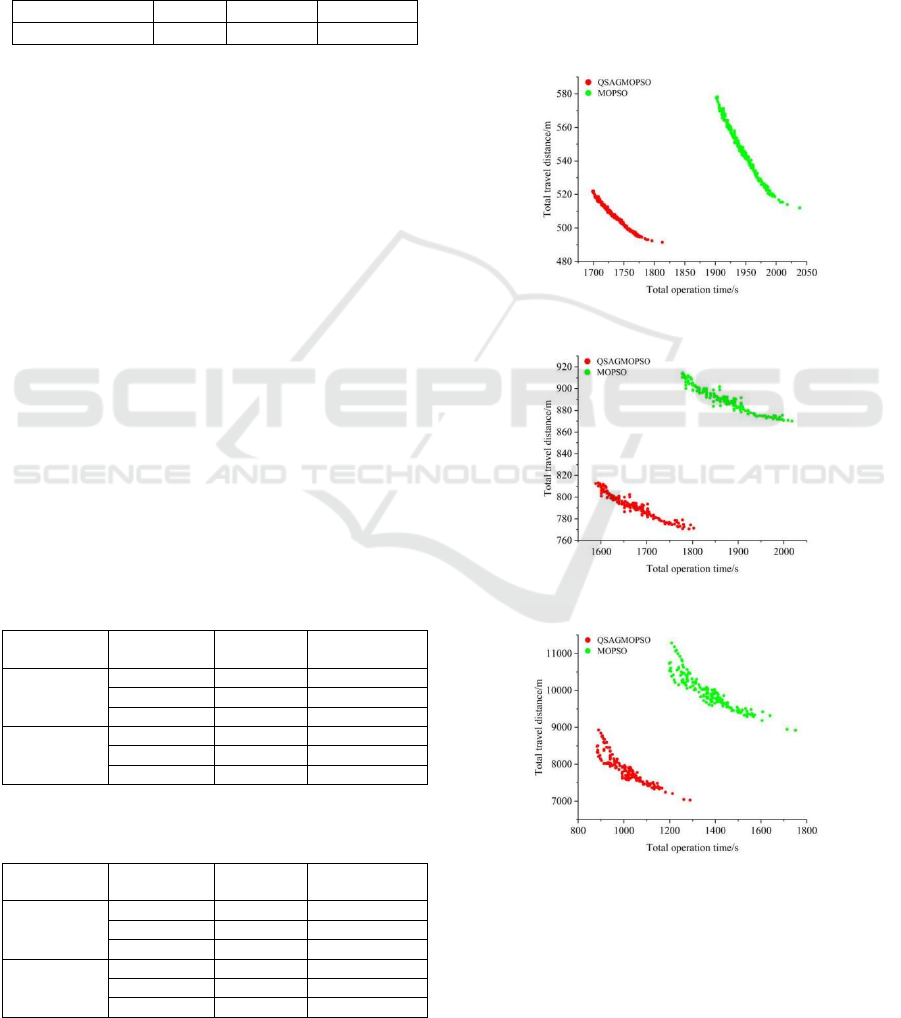
3.3 Example Simulation
A simulation was conducted in Matlab to address the
task assignment problem for multi-agent rail bolt
operation robots. The resulting comparison of the
algorithm's performance is illustrated in Figure 4 and
Figure 5.
From Figure 4 and Figure 5, it can be observed
that both algorithms were run 20 times across
different task quantity scenarios. Two multi-objective
optimization algorithms were used to record all
Pareto frontiers obtained in each instance. To further
evaluate the Pareto solution sets, two metrics were
introduced: Average Ratio (AR) and Spacing Metric
(SP). The results of these evaluations are presented in
Tables 4 and 5.
Table 4: Comparison of AR Values for Pareto Solution Sets
of Two Algorithms.
Number of
tasks
Number of
robots
MOPSO
QSAGMOPS
O
300
3 0.15 0.63
5 0.37 0.77
10 0.69 0.83
400
3 0.35 0.71
5 0.57 0.85
10 0.79 0.97
Table 5: Comparison of SP Values for Pareto Solution Sets
of Two Algorithms.
Number of
tasks
Number of
robots
MOPSO
QSAGMOPS
O
300
3 313.41 236.94
5 302.43 259.13
10 222.92 209.24
400
3 378.59 357.91
5 347.45 323.25
10 328.21 305.59
According to Tables 4 and 5, Table 4 compares the
AR values of the two algorithms. In the instance tests,
the AR values for the proposed QSAGMOPSO
algorithm were consistently higher than those for the
MOPSO algorithm, indicating that the
QSAGMOPSO algorithm produces higher-quality
solutions. Table 5 presents the average SP values for
each scenario. Across all scenarios, the proposed
QSAGMOPSO algorithm consistently achieved the
lowest average SP values, reflecting better
distribution and uniformity of solutions along the
Pareto front.
a
b
c
Figure 4: Comparison chart showing the completion of the
same task(300 pieces) by different numbers of robots. a:3
robots; b:5 robots; c:10 robots.
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
254
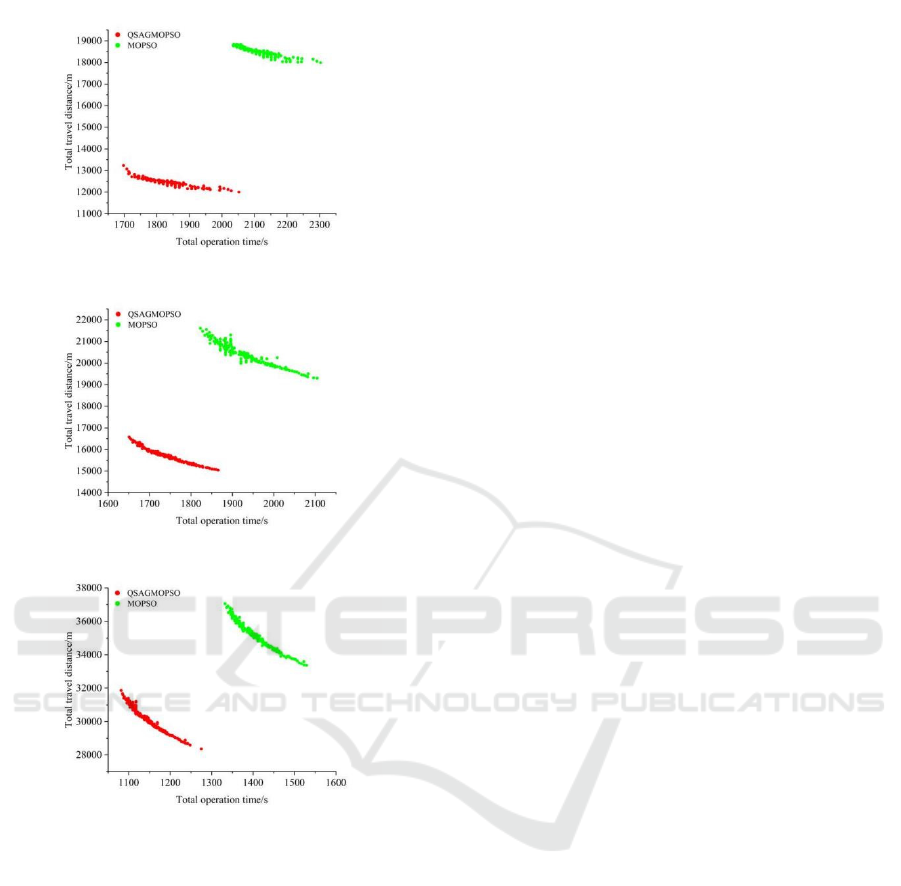
a
b
c
Figure 5: Comparison chart showing the completion of the
same task(400 pieces) by different numbers of robots. a:3
robots; b:5 robots; c:10 robots.
4 CONCLUSION
In this article, we address a previously unexplored
problem in multi-robot task assignment: the
collaborative task assignment of multi-agent rail bolt
operation robots. By introducing the concept of
collaborative control from multi-agent systems into
railway engineering, we redefine the fully automated
rail bolt robot as an intelligent agent capable of
independent decision-making. With a single
instruction from a staff member, the robot can
efficiently complete the heavy maintenance and
engineering tasks of track bolts during the skylight
period.
We further improved the classical multi-objective
particle swarm optimization (MOPSO) algorithm by
integrating quadratic sampling and a straightforward
adaptive grid partitioning method. These
enhancements tackle the problems of slow
convergence and getting stuck in local optima during
the later stages of the traditional PSO algorithm. The
simulation results demonstrate that the task
assignment method proposed in this paper greatly
enhances task efficiency.
In future research, we will refine the constraints
based on real-world engineering requirements and
further develop the task assignment model to meet
broader practical needs.
ACKNOWLEDGEMENTS
The authors acknowledge the support of Lanzhou
Jiaotong University for this study.
REFERENCES
Li, J., Hua, N., Zhu, K., et al. 2022. Leveraging joint
allocation of multidimensional resources for distributed
task assignment. J Opt Commun Netw, 14(5): 351-364.
Figueiredo E M N, Ludermir, T. B., Bastos-Filho, C. J. A.
2016. Many objective particle swarm optimization.
Information Sciences, 374: 115-134.
Lv, Z., Wang, L., Han, Z., et al. 2019. Surrogate-assisted
particle swarm optimization algorithm with pareto
active learning for expensive multi-objective
optimization. IEEE/CAA Journal of Automatica Sinica,
6(3): 838-849.
Zhou, T., Long, Q., Law K M Y, et al. 2022. Multi-objective
stochastic project scheduling with alternative execution
methods: An improved quantum-behaved particle
swarm optimization approach. Expert Systems with
Applications, 203: 117029.
Sun, B., Zeng, Y., Zhu, D. 2024. Dynamic task allocation in
multi autonomous underwater vehicle confrontational
games with multi-objective evaluation model and
particle swarm optimization algorithm. Applied Soft
Computing, 153: 111295.
Wang, C.-F., Liu, K. 2016. A novel particle swarm
optimization algorithm for global optimization.
Computational Intelligence and Neuroscience, 2016(1):
9482073.
Khan, S. U., Yang, S., Wang, L., et al. 2016. A modified
particle swarm optimization algorithm for global
optimizations of inverse problems. IEEE Transactions
on Magnetics, 52(3): 1-4.
Wang, F., Zhang, H., Han, M., et al. 2021. A mixed variable
Research on Cooperative Task Assignment of Multi-Agent Track Bolt Operation Robot Based on Optimized Multi-Objective Particle
Swarm Optimization
255

multi-objective particle swarm optimization algorithm
based on collaborative evolution for solving unmanned
aerial vehicle collaborative multi task allocation
problem. Journal of Computer Science, 44 (10): 1967-
1983.
Liu, Z. H., Zhang, J., Zhou, S. W., et al. 2013.
Coevolutionary particle swarm optimization using ais
and its application in multiparameter estimation of
pmsm. IEEE Transactions on Cybernetics, 43(6): 1921-
1935.
Goh, C. K., Tan, K. C. 2009. A competitive-cooperative
coevolutionary paradigm for dynamic multiobjective
optimization. IEEE Transactions on Evolutionary
Computation, 13(1): 103-127.
Song, X. F., Zhang, Y., Guo, Y. N., et al. 2020. Variable-size
cooperative coevolutionary particle swarm
optimization for feature selection on high-dimensional
data. IEEE Transactions on Evolutionary Computation,
24(5): 882-895.
Huang, M., Leung, V. C. M., Liu, A., et al. 2022. Tma-dpso:
Towards efficient multi-task allocation with time
constraints for next generation multiple access. IEEE
Journal on Selected Areas in Communications, 40(5):
1652-1666.
Li, Y., Zhang, Y., Hu, W. 2023. Adaptive multi-objective
particle swarm optimization based on virtual pareto
front. Information Sciences, 625: 206-236.
Lu, K., Tang, K., Dong, S., et al. 2024. Generalized-nash-
equilibrium-based pareto solution for transmission-
distribution-coupled optimal power flow. IEEE
Transactions on Power Systems, 39(2): 4051-4063.
Liu, B. 2017. Posterior exploration based sequential monte
carlo for global optimization. Journal of Global
Optimization, 69(4): 847-868.
Douc, R., Cappe, O. 2005. Comparison of resampling
schemes for particle filtering. ISPA 2005 Proceedings of
the 4th International Symposium on Image and Signal
Processing and Analysis, 2005: 64-69
Li, T., Bolic, M., Djuric, P. M. 2015. Resampling methods
for particle filtering: Classification, implementation,
and strategies. IEEE Signal Processing Magazine,
32(3): 70-86.
Kennedy, J., Eberhart, R. 1995. Particle swarm
optimization;. Proceedings of ICNN'95 - International
Conference on Neural Networks, vol. 1944, pp. 1942-
1948
Yan, J., Li, X., Liu, B. 2015. Application of Discrete
Particle Swarm Optimization Guo Tao Algorithm for
Multi UAV Collaborative Task Allocation [J] Journal of
National University of Defense Technology, 37 (04):
165-171.
Gao, J., Tan, Y., Li, D., et al. 2023. Discrete particle swarm
optimization algorithm for solving unrelated parallel
machine scheduling problems with service life
maintenance [J] Computer Integrated Manufacturing
System, 1-18.
Lu, Y., Li, B., Liu, S., et al. 2023. A population cooperation
based particle swarm optimization algorithm for large-
scale multi-objective optimization. Swarm and
Evolutionary Computation, 83: 101377.
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
256
