
Estimation of Hydrodynamic Dispersion Coefficient Under Saturated
and Unsaturated Conditions
Ziyi Jia
1,* a
, Hiroaki Terasaki
1b
, Min Wang
2c
, Jiehui Ren
2d
and Wen Cheng
2e
1
Graduate School of Engineering, University of Fukui, Fukui, 910-8507, Japan
2
Institute of Water Resources and Hydro-Electric Engineering, Xi'an University of Technology, Xi'an 710048, China
Keywords: Soil Salinization, Hydrodynamic Dispersion Coefficient, Dispersivity.
Abstract: In the study of soil salinization, the hydrodynamic dispersion coefficient is an important parameter for solute
transport. However, dispersion coefficients for soils require a great deal of time and effort, especially for silts
and clays, which can be complicated and prolonged to measure. In this study, the hydrodynamic dispersion
coefficients of silt and clay were determined by laboratory experiments and numerical analysis under different
saturation states. By comparing with the conventional method, the applicability of proposed method of to
quickly obtaining the unsaturated dispersion coefficient was verified. Additionally, by investigating the
relationship between the hydrodynamic dispersion coefficient and the soil pore water velocity, the empirical
formula of the soil hydrodynamic dispersion coefficient obtained.
1 INTRODUCTION
Soil salinization has become a common concern in
countries around the world. About 8.7 percent of the
world's land is threatened by salinization, and this
number continues to rise (FAO, 2021). China is one
of the countries with serious salinization and wide
distribution, mainly distributed in arid, semi-arid,
and coastal areas. In order to remove salinity from
soil, it is important to understand the transport
process of solutes in soil, which has been well
demonstrated in many research fields. The
hydrodynamic dispersion coefficient (D) is an
important parameter for controlling soil solute
transport. The D plays a crucial role in the simulation
and optimization of solute flux and subsequent
desalination methods.
For the measurement method of unsaturated D,
the traditional soil column method has a good effect
on sand, but it is time-consuming and labor-intensive.
In contrast, centrifugation method is fast, but the
equipment is expensive. The past developed suction
a
https://orcid.org/0000-0003-3688-2634
b
https://orcid.org/0000-0003-0087-8473
c
https://orcid.org/0000-0003-3110-266X
d
https://orcid.org/0000-0003-4491-5782
e
https://orcid.org/0000-0002-7231-7635
method can also be used to measure the dispersion
coefficient of sand. Although relatively cheap, it
takes a long time to reach a steady state, and the flow
needs to be adjusted. Also, due to the high cost and
time-consuming study of clay, silt, and loam, most of
the past studies have focused on the determination of
sand, highly permeable soils. In this paper, a
simplified quasi-steady-state suction method is
proposed to measure the unsaturated D of silty and
clay soils. Also, the D under the saturated state was
measured. In addition, by collecting the dispersion
coefficients of different types of soil in various
references, an empirical formula was obtained that
can be used to estimate the hydrodynamic dispersion
coefficient from the soil pore water velocity.
236
Jia, Z., Terasaki, H., Wang, M., Ren, J., Cheng and W.
Estimation of Hydrodynamic Dispersion Coefficient Under Saturated and Unsaturated Conditions.
DOI: 10.5220/0013628200004671
In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 236-240
ISBN: 978-989-758-764-1; ISSN: 3051-701X
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)

2 METHOD
2.1 Hydrodynamic Dispersion
Coefficient
Solute transport can be measured using the following
convective–dispersive equation:
z
Q
t
C
t
C
∂
∂
=
∂
∂
+
∂
∂
θ
θ
(1)
where C is the salt concentration (kg/m
3
); θ is the
volumetric water content (m
3
/m
3
); t is the elapsed
time (s), z is position or depth (m); and Q is the solute
flux (kg/(m
2
·s)), which can be defined as the sum of
convective and hydrodynamic dispersive fluxes:
z
C
DqCQ
∂
∂
−=
θ
(2)
where q is the Darcy flow velocity (m/s), and D is the
hydrodynamic dispersion coefficient (m
2
/s), which is
expressed as the sum of molecular diffusion
coefficient (D
c
) and the mechanical dispersion
coefficient (D
m
):
D=D
c
+ D
m
(3)
In this study, the value of D
c
was set to 1.65 × 10
-
9
m
2
/s (Castillo et al., 1993). D
m
is represented by
D
m
=λv
α
(4)
where λ is the dispersivity (m), v is the average pore
water velocity (m/s), and α is generally equal to 1.
2.2 Experimental Design
2.2.1 Experiment for Unsaturated Soils
Three experimental cases using fluvo-aquic soil (a
silty soil collected from Jiangsu, China) and kaolin
clay soil were considered. The experimental setup is
shown in
Figure
1. The inner diameter of the soil
column was 25 mm, and the height was 70 mm,
which was divided into two layers. A TDR sensor
(TRIME-MUX6) was inserted near the surface of the
lower column to measure the variation in salinity.
Water suction was achieved using a vacuum pump
(DA60-D). The suction flask, gas jar, and a small
column attached at the end (filled with silica gel)
were used to collect water and water vapor. The
following experimental steps were followed: (1)
uniformly mix the soil with fresh water, and fill in
the lower soil column to a certain θ value; likewise,
fill in the upper soil column with soil mixed with
saline water (C = 0.5%) to same θ value; (2) start
water suction using the vacuum pump; (3) measure
the drainage water mass using electrical balance, and
monitor the output of the TDR sensor. To investigate
the quasi-steady-state condition, both the upper and
lower soil columns were mixed with fresh water, and
a preliminary test was conducted before the
experiment.
Figure 1: Experimental setup.
2.2.2 Experiment for Saturated Soils
Five experimental cases using fluvo-aquic soil and
Tohoku paddy soil (collected from Natori, Japan)
were considered. As shown in
Figure
2, the
experimental apparatus comprises a soil column
made of vinyl chloride, with an inner diameter of
0.107 m, pump (WP1000, Welco Co., Ltd), water
tank, funnel, electronic balance (PB4002-S, Mettler
Toledo Co., Ltd), Four-electrode salinity sensor, and
data logger (CR1000, Campbell Scientific, Inc.). The
depths of the sensors from the soil surface were 110
mm, 190 mm, 270 mm, and 350 mm. The experiment
was conducted by adopting the following procedure:
(1) The air-dried soil was screened and evenly filled
into the soil column (bulk density of 1.6 g/cm
3
); (2)
Kept the head of the water tank constant and
continuously supplied the fresh water from bottom of
the column to attain saturation by capillary; (3) After
saturation, the NaCl solution with C of 10 kg/m
3
supplied from top of the column and kept the water
level constantly; (4) Changes in the electrical
conductivity (EC) value of the sensor were observed;
(5) When the EC value of the bottom sensor was
constant, the experiment was terminated.
Estimation of Hydrodynamic Dispersion Coefficient Under Saturated and Unsaturated Conditions
237
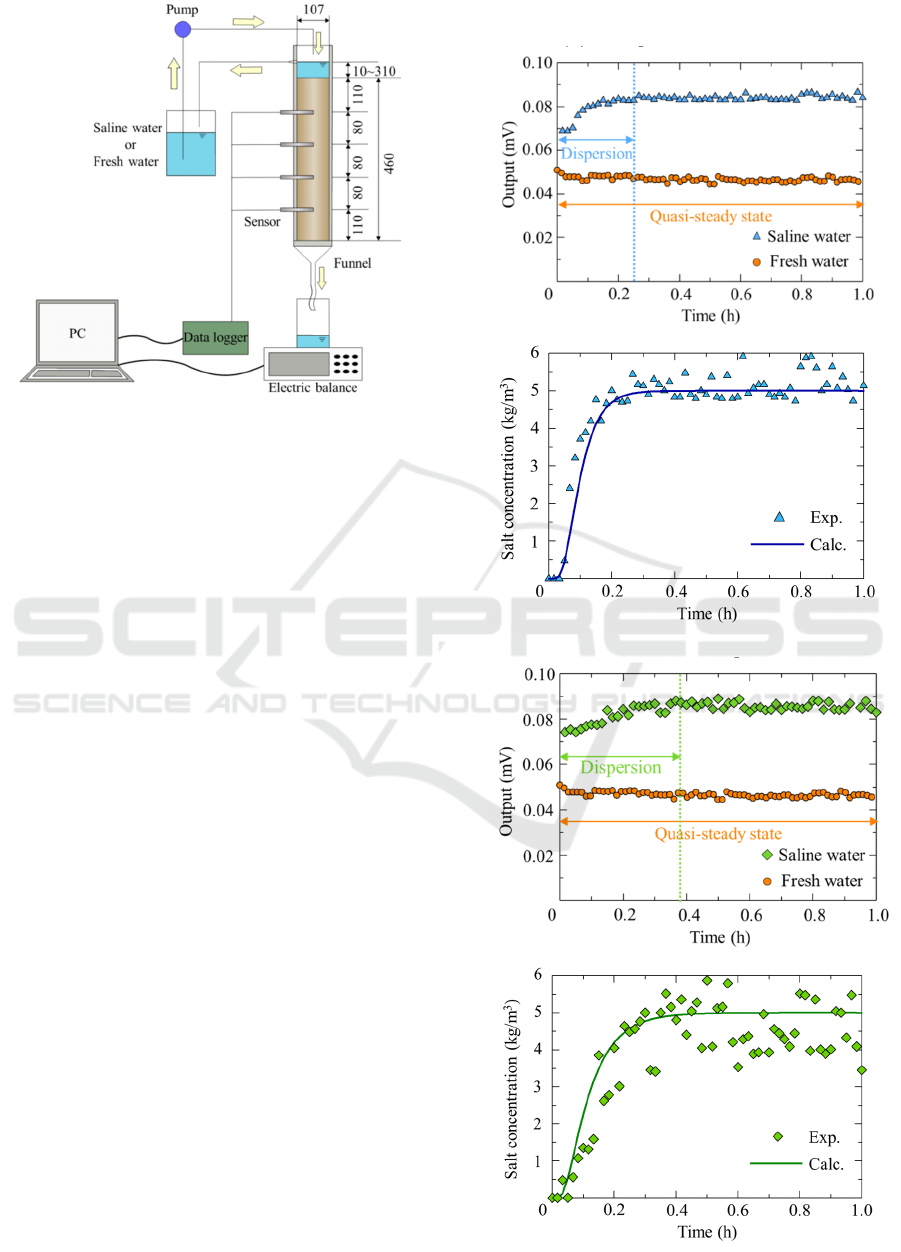
Figure 2: Experimental equipment (Unit: mm).
3 RESULTS AND DISCUSSION
3.1 Hydrodynamic Dispersion
Coefficient of Unsaturated Soil
Figure
3 shows the time variation in the output values
of the TDR sensor and salt concentration in Case1–3.
Cases 1 and 2 correspond to fluvo-aquic soil at two
flow rates. Case 3 corresponds to kaolin clay soil. No
significant changes in the TDR sensor output values
were observed in the freshwater test until 1.0 h after
the start of the experiment, which is considered a
quasi-steady state. In contrast, the TDR sensor output
value in the saline water experiment increased for
approximately 0.25 h, after which it showed a
constant value. Further, θ, C, and the TDR sensor
output obtained from the preliminary test revealed
that the salinity at the sensor position reached 0.5%
after 0.25 h.
The pore water velocity was calculated from the
time variation in the drainage mass during the quasi-
steady-state condition. The v values of the fluvo-
aquic soil were approximately 4.45 × 10
-6
m/s and
3.93 × 10
-6
m/s. The salt concentration variation
curve was obtained by converting the sensor output
value, and the dispersion coefficients were
determined by fitting the breakthrough curve for the
experimental and calculated values. As can be seen
from the breakthrough curve in Figure 3, the
calculated and experimental values have good fitness.
The D values of the fluvo-aquic soil were
approximately 2.50 × 10
-9
m
2
/s and 5.00 × 10
-9
m
2
/s,
and that of kaolin clay was 1.25 × 10
-9
m
2
/s.
Noticeably, the simplified suction method proposed
in this study yields quick results.
a)Case1– Fluvo-aquic soil
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
238
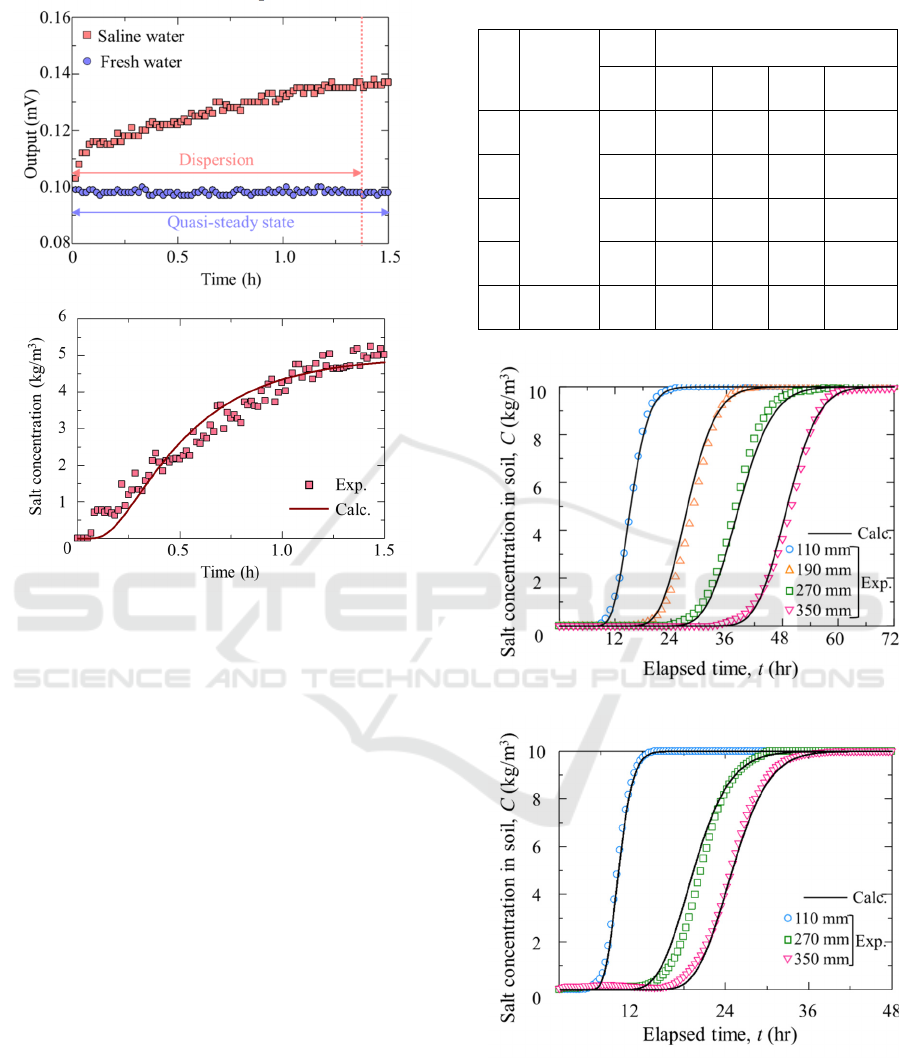
b
)Case2– Fluvo-aquic soil
c)Case3–
K
aolin clay
Figure 3: Time variation of sensor output and breakthrough
curve of Case1–3.
3.2 Hydrodynamic Dispersion
Coefficient of Saturated Soil
Case1–4 of fluvo-aquic soil and Case 5 of Tohoku
paddy soil determined their corresponding D at
different v as shown in Table 1. Figure 4 shows the
breakthrough curve of Case 3 and Case 5 under the
average value of 8.04×10
-7
m/s (v), by fitting the
experimental and calculated values. It can be seen
that the C changes with respect to time and space.
After adding the NaCl solution, C increased
gradually until it approached 10 kg/m
3
of the C.
Calculated results showed sound agreement. Due to
the scale dependency of D (Moradi et al., 2020), the
values calculated separately for each sensor from top
to bottom.
Table 1: Dispersion coefficient of each sensor at different
pore water velocity in Case1–5.
No. Soil type
v
D of different depth (m
2
/s)
(m/s)
110
mm
190
mm
270
mm
350 mm
Case
1
Fluvo-
aquic soil
3.18E-
06
-
3.50E-
09
3.50E-
09
3.50E-09
Case
2
1.61E-
06
9.50E-
10
1.00E-
09
1.00E-
09
1.00E-09
Case
3
8.19E-
07
4.50E-
09
5.40E-
09
5.50E-
09
3.50E-09
Case
4
1.23E-
06
3.50E-
09
3.80E-
09
6.00E-
09
5.50E-09
Case
5
Tohoku
p
addy soil
1.77E-
06
7.00E-
09
-
1.80E-
08
2.30E-08
a)Case 3
b
)Case 5
Figure 4: Breakthrough curve of the saturated soil.
3.3 The Relationship between D and v
As the D of each type of soil is different, and the
measurement is complicated, the D of different types
Estimation of Hydrodynamic Dispersion Coefficient Under Saturated and Unsaturated Conditions
239
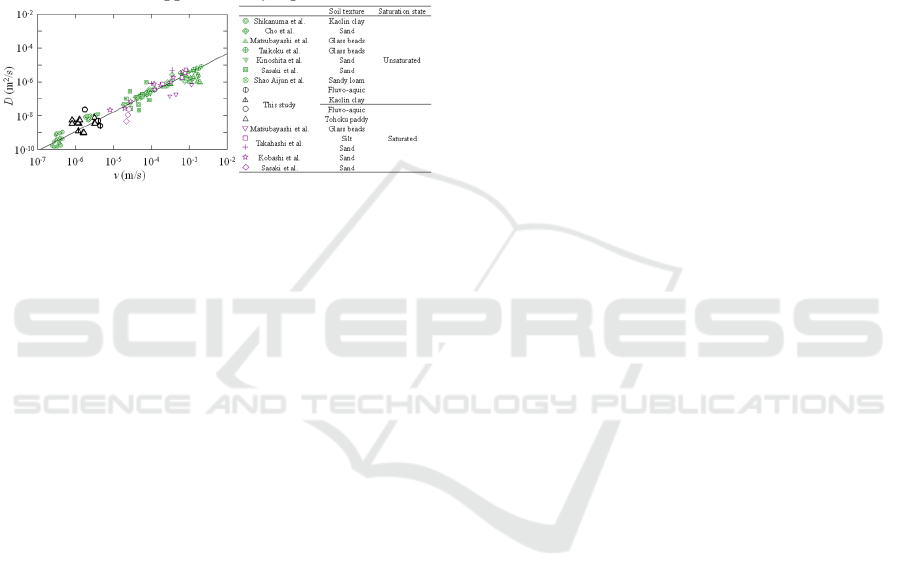
of soil in past studies are collected and summarized
in Figure 5. The relationship between the D and v
obtained in this experiment and those in the
references (Shikanuma et al., 2003; Kobashi et al.,
2004; Cho et al., 1981; Matsubayashi et al., 1997;
Taikoku et al., 1997; Kinoshita et al., 2003; Sasaki et
al., 1986; Shao et al., 2002; Takahashi et al., 2005).
The experimental values obtained in this study
generally conformed to the D-v liner line, which is
represented by:
D = 0.0095v
1.15
(5)
where the value of dispersivity is approximately
0.0095 m, and α is approximately equal to 1.15.
Figure 5: Relationship between D and v in saturated and
unsaturated soil.
4 CONCLUSIONS
In this study, the hydrodynamic dispersion
coefficients of fluvo-aquic soil and kaolin clay under
unsaturated state and fluvo-aquic soil and Tohoku
paddy soil under saturated state were investigated.
Proposed simplified suction method in this study
yields quicker results than the conventional methods.
Additionally, by collecting the different types of soil
in past studies and combing the values in this study,
the dispersivity of different saturation conditions
were measured at 0.0095 m. Therefore, when the soil
dispersion coefficient cannot be experimentally
measured under limited conditions, it can be
calculated using the dispersivity obtained in this
study when the soil pore water velocity is known.
However, the measurements are relatively few. In the
future, we will accumulate experimental data and
compare that with data from other measurement
methods to verify its accuracy.
REFERENCES
FAO, 2021. World map of salt-affected soils launched at
virtual conference.
Castillo, R., Garza, C., 1993. Temperature dependence of
the mutual diffusion coefficients in aqueous solutions
of alkali metal chlorides[J]. International Journal of
Thermophysics, 14(6): 1145–1152.
Moradi, G., Mehdinejadiani, G., 2020. An experimental
study on scale dependency of fractional dispersion
coefficient[J]. Arabian Journal of Geosciences,
13(11), 409.
Shikanuma, Y., Izawa, J., Kusakabe, O., 2003. Advective
diffusion of pollutants in clay soil using drum
centrifuge[J]. Japanese Geotechnical Society, 38:
2345–2346.
Kobashi, H., Miki, H., Hirayama, M., Hishiya, T.,
Yamamoto, H., Ohkita, Y., 2004. The determination of
longitudinal dispersivity in predicting the influence of
ground contamination[J]. Japan Society of Civil
Engineers, 764(3): 53–67.
Cho, T., Tanaka, A., Kodani, Y., 1981. A new method of
determining the dispersion coefficient of salt in soil[J].
Bull. Sand Dune Research, 20: 11–16.
Matsubayashi, U., Devkota, L.P., Takagi, F., 1997.
Characteristics of the dispersion coefficient in miscible
displacement through a glass beads medium[J].
Journal of Hydrology, 192: 51–64.
Taikoku, T., Suganuma, M., Matsubayashi, U., Takagi, F.,
1997. A study on the advection and diffusion
characteristics in a heterogeneous porous medium[C].
Japan Society of Civil Engineers Annual Meeting, Ⅱ–
185.
Kinoshita, K., Hayashi, S., Oka, T., 2003. Understanding
dispersion phenomena in unsaturated permeation flow
based on vertical column experiments[J]. Japan
Society of Civil Engineers, 2: 71–72.
Sasaki, Y., Sato, K., Fukuhara, T., 1986. Experimental
study on diffusion and dispersion coefficients of
solutes in unsaturated seepage flow[C]. Japan Society
of Civil Engineers Annual Meeting, Ⅱ–91.
Shao, A., Liu, G., Yang, J., 2002. In-lab determination of
soil hydrodynamic dispersion coefficient[J]. Acta
Pedological Sinica, 39: 184–189.
Takahashi, N., Nakata, M., Yamamoto, Y., 2005. Study on
hydrodynamic dispersion and absorption
characteristics of soil. Sumitomo Mitsui Construction
Technology Research Report, 3: 65–69.
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
240
