Real-Time Monitoring of Displacement of Machine Vision Bridge

Based on YOLOV5-MLR Study

Dong Ran

1,2,* a

, Jianxu Long

1,2 b

, Zhuan Wang

1,2

, Xiaoyong Zhang

1,2

and Qian Guo

1,2

Department of Architectural Engineering, Guizhou Communications Polytechnic University, Guiyang 551400, China

Key Laboratory of High Performance Repair Materials, Guizhou Communications Polytechnic University,

Guiyang 551400, China

Keywords: Bridge Monitoring, Target Detection, Target Recognition, Displacement Monitoring.

Abstract: Currently, the bridge maintenance tasks are arduous, and the health condition of bridges is of the utmost

importance to ensure traffic safety. In order to achieve real-time monitoring of bridges and reduce monitoring

costs, it is necessary to seek practical and effective solutions. Research has found that due to the influence of

environmental and other factors, the precision and accuracy of traditional machine vision monitoring methods

are insufficient. Therefore, this paper proposes a method called the YOLOV5-MLR improved algorithm. This

algorithm adopts more complex texture targets and can better distinguish the surrounding environment during

the monitoring process, thus improving the accuracy. In addition, during the calculation process, the algorithm

refines the precision unit to the pixel level and can achieve a precision level at the sub-millimeter level. After

a series of experimental verifications, the results show that the YOLOV5-MLR improved algorithm has high

robustness, and the monitoring error is controlled at the millimeter level, meeting the specification

requirements for bridge monitoring. This new algorithm provides important technical support for bridge

health monitoring and is expected to play a key role in the field of bridge monitoring.

1 INTRODUCTION

Currently, for the monitoring of buildings, slopes and

bridges, the main equipment used are total stations

and RTK. The total station has relatively high

precision and is the mainstream equipment for

monitoring. (Liu et al., 2024; Liao et al., 2024; Shan

et al., 2024) However, it requires continuous

operation by personnel to complete the measurement

work at monitoring points. Meanwhile, the cost of

total station equipment is relatively high. The

positioning accuracy of RTK is around 2 cm, which

to some extent has an impact on the monitoring

results. In addition, after collecting data through

sensors, some scholars conduct manual marking in

the way of image annotation. Although this method

has relatively high precision, its efficiency is low and

it requires post-processing for coordinate staking.

Some scholars also detect the center of the target

by means of corner detection (Liu, Y et al., 2024,

https://orcid.org/0009-0004-6775-2992

https://orcid.org/0000-0003-3067-448X

Shang et al., 2024; Bao et al., 2024). For example,

(Busca et al., 2024) developed a vision-based

displacement sensor system by utilizing pattern

matching, edge detection and digital image

techniques. Two different visual sensors were used to

track the high-contrast target fixed on the bridge and

measure the vertical displacement of the bridge.

Harris corner detection sets a predefined rectangular

window, moves it slightly in all directions in the

image, and identifies corners according to the gray

level changes of the image inside the window (Shang

et al., 2024; Xiang et al., 2010). SUSAN corner

detection adopts a nearly circular template and sets

the center point of the template as the core point (Lin

et al., 2010). A pixel point and a sufficient number of

different regional pixels around it are defined as

FAST corners (Ding et al., 2013).

For uncomplicated targets, this method can

quickly and accurately identify the center of the

target. However, when affected by the surrounding

220

Ran, D., Long, J., Wang, Z., Zhang, X., Guo and Q.

Real-Time Monitoring of Displacement of Machine Vision Bridge Based on YOLOV5-MLR Study.

DOI: 10.5220/0013628000004671

In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 220-227

ISBN: 978-989-758-764-1; ISSN: 3051-701X

environment and the problems of the camera itself,

resulting in low-quality collected images or in the

case of targets with complex textures, using the

corner detection method will simultaneously obtain

multiple detection targets, and the accuracy will be

interfered to some extent. Moreover, manual

processing will still be required in the later stage.

In addition to corner detection, some scholars also

use tracking and target detection methods for

displacement detection. (Lee et al., 2012) proposed a

corner measurement system for large civil structures

based on computer vision. By utilizing image

processing technology, they tracked artificial targets

and calculated the rotation angles. (Hu et al., 2022)

used the computer vision-based method to identify

the displacements of multiple targets. At present,

deep learning methods are mostly adopted for target

recognition, such as the YOLO series of algorithms

for target detection (Zhou et al., 2023), which can

quickly identify the positions of targets and quickly

obtain the central coordinates of targets according to

the prior boxes. However, due to the influence of

factors such as the shooting angle and the target

angle, the coordinates of the target center are not

accurate. Therefore, based on the YOLOv5 target

detection algorithm, this paper adds the MLR

(Multiple Linear Regression) method to quickly and

accurately determine the central position of the target

according to the gray values of the image.

2 DISPLACEMENT MONITORING

BASED on the IMPROVED

YOLOV5-MLR ALGORITHM

2.1 The Principle of Displacement

Measurement in Computer Vision

Two-dimensional coordinate displacement

monitoring of the monitored object is carried out

through the means of computer vision. The

calculation is mainly based on several parameters

such as the distance from the camera to the monitored

object, the focal length of the camera, the image

resolution and the number of displacement pixels, as

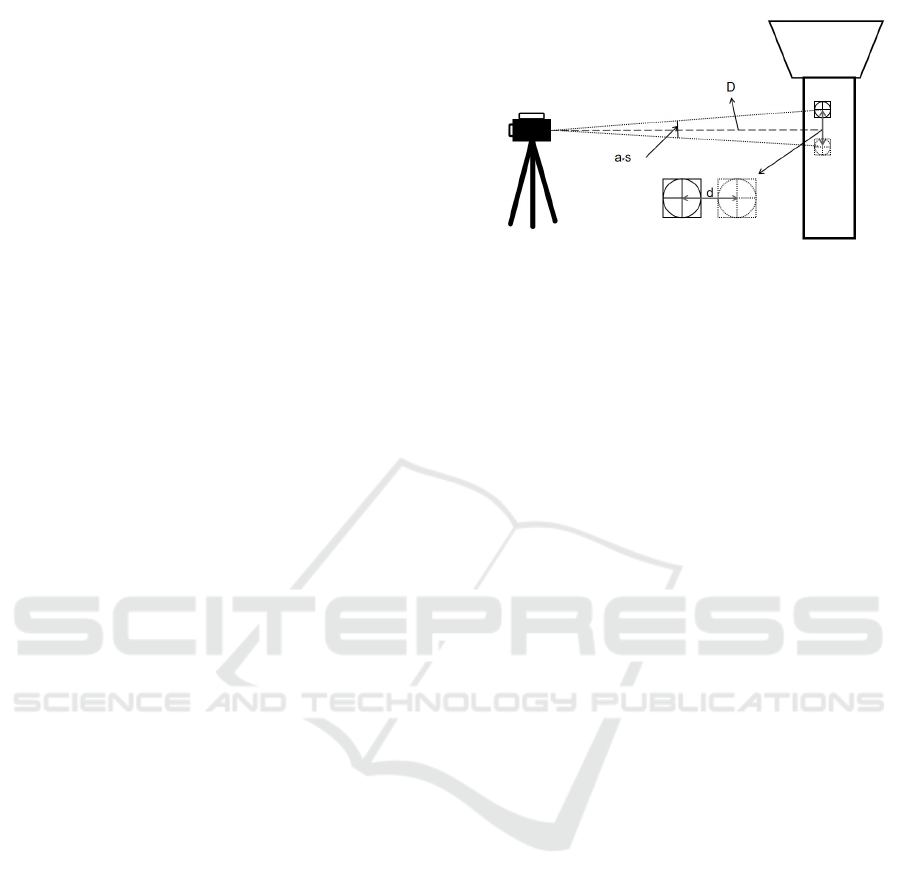
shown in the following Figure 1:

Figure 1: Schematic diagram of the target displacement

measurement with computer vision.

Among them, D represents the distance from the

camera to the target, a represents the pixel size of the

camera, s represents the number of pixels by which

the target has changed before and after displacement,

and the focal length f is a known value. According to

formula (1), the distance of the target before and after

displacement can be calculated.

d=D∗a∗s

⁄

(1)

During the entire calculation process, is a

variable that requires measurement and calculation.

Therefore, only by accurately obtaining the centers of

the targets before and after the change can the

displacement of the targets be calculated accurately.

When the value of increases, a single pixel also has

a relatively large impact on the accuracy of the

measurement data. Hence, it is necessary to adopt a

high-precision method for obtaining the centers of the

targets so as to ensure the accuracy of bridge

displacement monitoring.

2.2 Extraction of the Initial Coordinates of

Feature Points Based on YOLOV5

Affected by factors such as the environment, the

angle of the target, the deformation of the target, and

the bounding box (BOX), although the YOLOV5

algorithm cannot accurately identify the center point

of the target, it can obtain an approximate coordinate.

It can quickly calculate the center coordinate of a

target through the four corner points of the bounding

box. Therefore, the research in this paper uses the

YOLOV5 algorithm to identify the target and obtain

the initial coordinates.In the early stage, the

LabelImg software was used to label the targets so as

to obtain a model training sample library. Since the

environment has interference on target identification,

especially when monitoring bridges, the surrounding

white clouds may be misidentified. Therefore, the

Real-Time Monitoring of Displacement of Machine Vision Bridge Based on YOLOV5-MLR Study

221

targets used are not pure white-background

targets.Based on the sample library and labels, the

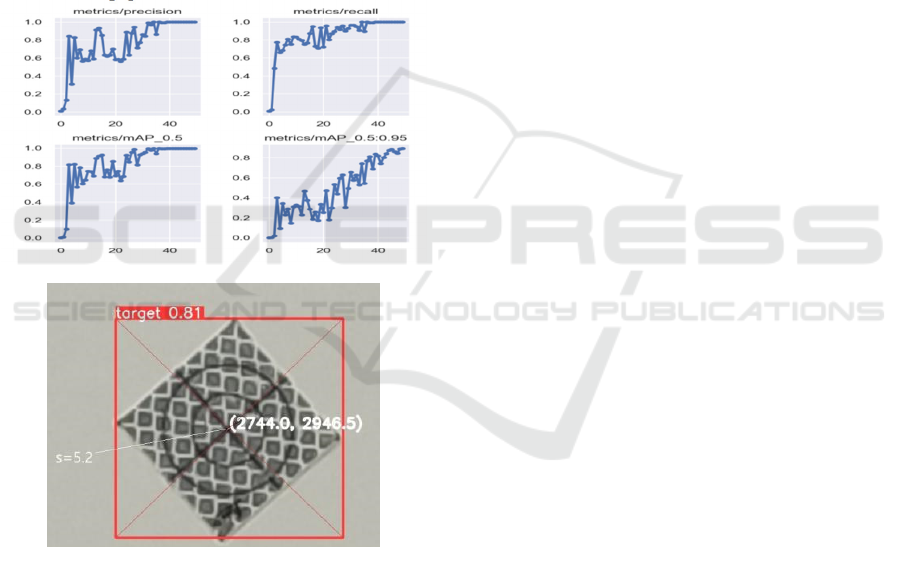
YOLOV5 algorithm was used for model training. As

it is a one-class model training and the characteristic

information of the targets is rather special, the

accuracy rate of the model training reaches 99%, as

shown in Figure 2(a).The calculation method for the

coordinates of the center point of the BOX is x







)/2, y



=(y





)/2 ,Thus, the

coordinates of the center point of the target are

obtained. As shown in Figure 2(b), it can be seen

from Figure 2(b) that the center of the target can be

roughly identified by YOLOV5. However, there is

still a certain error compared with the actual center of

the target. The error is 5.2 pixels, which is also the

intersection recognition problem that needs to be

solved in the paper.

(a)Training of the target recognition model

(b) Recognition of the central coordinates of the target

Figure 2: Target training results and identification.

2.3 YOLOV5-MLR Improved Algorithm

As shown in Figure 2(b), due to the complexity of the

target image, which is not just in black and white, this

type of target can avoid the misidentification of the

target caused by the surrounding environment. Since

there are many other interfering backgrounds on the

target itself, multiple corner points will be detected

simultaneously when using the corner detection

algorithm, and the center of the target cannot be

accurately located. Therefore, the research in the

paper first employs the YOLOV5 algorithm to

conduct a rough identification of the center of the

target.Obtain the initial values of x



、y



and z



for

the target center.Among them, x



represents the

initial abscissa,y



represents the initial ordinate, and



represents the gray value. After obtaining the

initial coordinates, the extraction of the target center

can be carried out. The main process is as follows:

(1) Acquisition of the minimum grayscale value

within the region. Based on the initial

coordinates obtained by the YOLOV5 algorithm,

since the inner circle radius of the target is 9 mm,

in order to avoid retrieving the pixels on the

circle, during the retrieval process, the pixels

within the adjacent 5 mm range are retrieved.

The number of pixels is represented by q, and

the specific formula is as follows.

q=d∗f D∗a

⁄

(2)

Among them, D represents the distance from the

camera to the target, a stands for the size of a pixel,

and f represents the focal length. d refers to the

retrieval radius, and its value is 5 mm.

The value of q can be calculated through Formula

(2). The magnitude of q is determined by the distance

D and the focal length f. In addition, on the basis of

the initial coordinates of the target, the target searches

for the minimum gray value within q adjacent pixels.

Usually, this minimum value is mainly distributed on

the two intersection lines of the target.

(2) Acquisition of the coordinates of the pixels that

meet the requirements, including the values,

where represents the horizontal and vertical

coordinates of the pixel in the image, and the

value represents the grayscale value of the pixel.

According to the grayscale information of the

initial coordinates, extract all the points within q

pixels around the point and with a value less

than min(z



)+30, as shown in the following

formula.



−q<x<x



−q<



zmin(z



)+30

(3)

The research in the thesis processes the images

through Python programs to obtain all the pixels that

meet the conditions and whose values are less than

70. The search results are shown in the following

figure.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

222

Figure 3: Points with gray values less than 70 within the

area.

(3) Acquisition of the initial intersection line

equation: No matter at what angle the cross

intersection line at the center of the target is

located, the equations of the two intersecting

straight lines can be extracted.

First, randomly select two points ( 𝑥



,𝑦



) and

( 𝑥



,𝑦



) from the point library that satisfies the

condition of being less than min(z



) +

30.Meanwhile, it is required that the distance

between the two points should be greater than 2q

pixel values, where q is a positive integer. If the

distance from the camera to the target decreases or

the camera resolution increases, the value of q will

increase correspondingly. On the contrary, if the

distance from the camera to the target increases or the

resolution decreases, the value of q will decrease

accordingly. Therefore, this value is adjusted

according to the actual visual measurement. This can

ensure that the constructed linear equations are

distributed as close to the intersection lines of the

target as possible. Meanwhile, it can avoid

constructing linear equations with adjacent points,

which would otherwise increase the amount of

calculation. Therefore, setting a threshold for the

distance between two points can improve the

calculation efficiency of the target linear equations.





−



)(x



−x



)

⁄



−A



i,j=1......n























1......n

(4)

As shown in Equation (4), in the equation,A



represents the slope, C



represents the intercept, B



1, and d



is the distance from any point in the point

library where z is less than min(z



)+30 to the

generated straight line. Meanwhile, it is required that

the number of pixels satisfying d



< 1 should be

greater than 4q, where q is a positive integer.

Therefore, two straight line equations of relatively

high quality can be obtained through this method.



x+B





x+B



(5)

As shown in Equation (5), B



and B



are

constants with a value of 1.A



and A



are slopes.C



and C



are intercepts. And the slopes A



and A



a r e

two values with opposite signs.As shown in Figure 3,

since the two intersecting straight lines are

perpendicular to each other, the signs of the slopes of

the equations of the two straight lines must be

different. From this, two straight lines that are

basically close to the target straight lines can be

obtained.

(4) Inspection of the equations of the two

intersection lines and acquisition of the optimal

straight lines. The intersection line equations

obtained through step (3) are relatively close to

the target intersection line equations. The error

of the intersection point pixels obtained through

these intersection line equations is within the

range of 2 - 5 pixels, but there still exists a

certain degree of error.According to the

displacement calculation formula, d=(D∗a∗

s)/f,Among them, "a" represents the pixel size,

"D" stands for the distance from the camera to

the target, "s" represents the number of pixels,

and "f" represents the focal length. The camera

used in the research of the paper has a fixed focal

length of 12 mm, and a 2x zoom with a focal

length of 24 mm. The pixel size is 2 μm, and the

resolution is 48 million pixels. When the

distance is 1 m, the precision is 0.08 mm, and

when the distance is 10 m, the precision is 0.8

mm. When the error is 5 pixels, the maximum

error is 0.4 mm at a distance of 1 m, and the

maximum error is 4 mm at a distance of 10 m.

Generally, the error requirement for bridge and

building monitoring is at the millimeter level. If

the error is controlled within 2 pixels, the

maximum error is 0.16 mm at a distance of 1 m,

and the maximum error is 1.6 mm at a distance

of 10 m, which meets the monitoring

requirements. When the distance is relatively

close, the intersection coordinates obtained from

the initial intersection line equation are

sufficient to meet the requirements of bridge

monitoring. As the distance increases, the error

gradually increases. To further improve the

precision, inspection and optimal straight line

selection are carried out on the basis of step (3).

Through step (3), n pairs of straight line equations

that meet the requirements can be obtained.

Real-Time Monitoring of Displacement of Machine Vision Bridge Based on YOLOV5-MLR Study

223

Therefore, in order to further reduce the error in the

calculation of the intersection points of the target, it

is necessary to select the two straight lines with the

highest precision from the n pairs of intersection line

equations. Thus, after obtaining n pairs of straight

line equations that meet the requirements, the target

straight lines are selected by the substitution method.



𝑥





=𝑦



𝑦



− 𝑦



<=1

𝑥





=𝑦



𝑦



− 𝑦



 <=1

(6)

Among them,𝑥



、𝑦



, 𝑥



and 𝑦



are the points in

the point library where z is less than <min(z



30.In the inspection process, 4q points that meet the

condition of equation (6) are required, where q is a

positive integer. Two target straight lines are

determined by this method.

(5) Target center calculation. Conduct intersection

calculation based on 𝐴



, C



, 𝐴



a n d C



obtained

in step (4). This intersection is the target center.

Here, B



=1 and B



=1. The coordinates of the

target center are shown in the following formula:



=(B





−B





)/(A





−A





)



=(A





−A





)/(A





−A





)

(7)

3 COMPARATIVE ANALYSIS on

the APPLICATION of the

IMPROVED YOLOV5-MLR

ALGORITHM

3.1 Error Analysis of the Improved YOLOV5-

MLR Algorithm

In terms of error analysis, the research in the thesis

conducts error analysis from two aspects. For the first

aspect, a comparative analysis is carried out

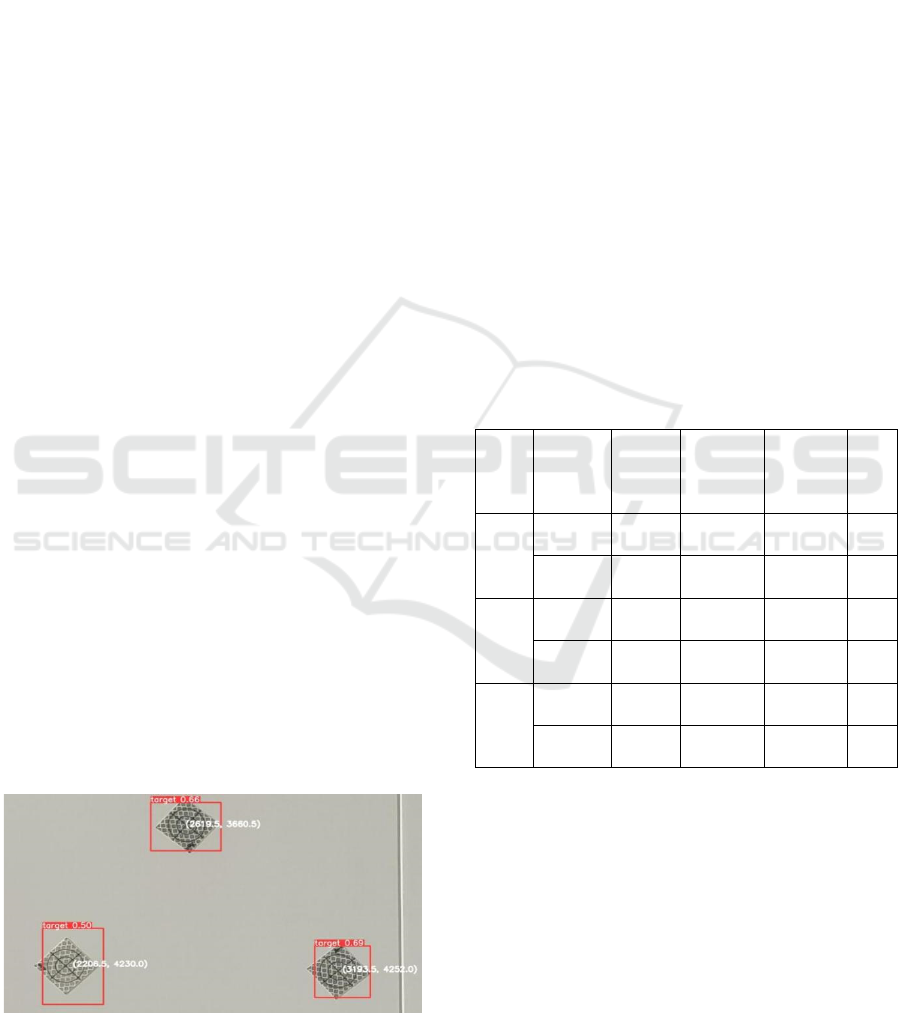
longitudinally for a single target. During the analysis

process, three targets at different distances from the

camera are selected, as shown in Figure 4.

Figure 4: YOLOV5 Target center coordinates acquisition.

The equations of n pairs of intersection lines can

be obtained through certain steps. The following are

the slope and intercept values of any pair of equations

among the three targets. Firstly, use YOLOV5 to

obtain the coordinates of the targets. Secondly, use

the equations of the intersection lines to obtain the

initial coordinates of the intersection

points.Respectively for 𝐴



=1.06,C



21915 , 𝐴



=−1,C



= 6407.0 , 𝐴



=1,C



1030 , 𝐴



= −1.14, C



= 6652.14 , 𝐴



−0.94, C



= 7228,𝐴



=1.1,C



= 753.

Finally, substitute the known coordinates for

checking and determine the optimal intersection line

equation and coordinates.Its slope and intercept are

𝐴



= 1.085714, C



= 1861.342857, 𝐴



−1.028571, C



= 6470.714285, 𝐴



−1.088235, C



= 6509.411764, 𝐴



0.939394, C



= 1189.939394, 𝐴



−0.787234, C



= 6750.148936, 𝐴



1.11764705, C



= 698 respectively.

The coordinates of YOLOV5, the initial

coordinates, the optimal coordinates and the real

coordinates are shown in Table 1.

Table 1: Individual target coordinates at different stages.

Poin

num

Coordi

nates

YOL

OV5

Initial

value

Optimal

value

Tru

val

ue.

x 2206

2180.58

2524

2180.10

8844

218

y 4230

4226.41

7476

4228.31

7551

422

x 2620

2627.16

8224

2623.49

4007

262

y 3660

3657.16

8224

3654.43

3764

365

x 3194

3174.01

9608

3177.17

9455

317

y 4252

4244.42

1569

4248.96

5245

424

For the three targets, through longitudinal analysis

of each individual target, it was found that during

the process of obtaining the central coordinates of

the three targets, the errors of the iterative

coordinates were all the smallest, and the errors of

the optimal coordinates tended to be around 0.

The

error results are shown in Figure 5.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

224

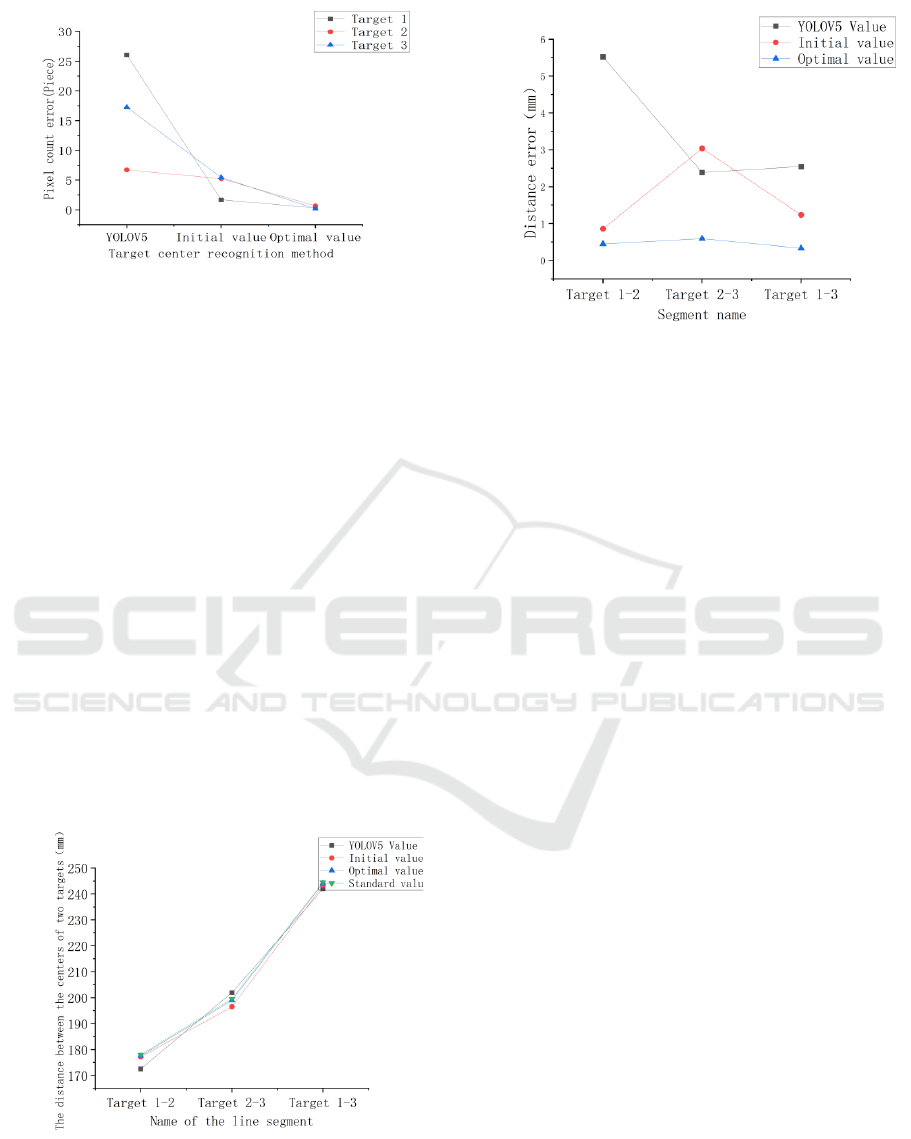
Figure 5: Error statistics plots for the different methods.

In addition to the longitudinal comparison, the

thesis research also conducts a lateral comparison

based on the actual distances. As shown in the Figure

6 below, it presents the distances between two targets

calculated by different methods. Among them, the

distance between the camera and the target is 1,469

mm. Through analysis, it was found that the

deviations between the distances between the two

targets obtained by YOLOV5 and the true values

were relatively large. And the initial values of the

distances between the two targets obtained through

the intersection line equation were relatively close to

the true values, but there were still errors and the

results were unstable, which was caused by

randomness. However, the distances between the two

targets calculated according to the optimal linear

equation were close to the true values, with errors

within 1 mm. Through practical analysis, it was

discovered that using the improved YOLOV5-MLR

algorithm for target displacement monitoring has a

relatively good effect, with high precision and low

errors.

Figure 6: Statistical map of the actual distance between the

two targets.

3.2 Application of the YOLOV5-MLR

Improved Algorithm in Target

Displacement Monitoring

This paper conducts a practical demonstration of

bridge displacement monitoring with the on-campus

bridge training base as the application scenario. The

selected bridge is the Kunpeng Bridge on campus,

which is a rather distinctive bridge and a training

bridge integrating monitoring and detection.

Therefore, applying the target-based visual

displacement monitoring technology to this bridge

has relatively high teaching value. In this practical

application, the target is attached to the bridge pier

for monitoring the lateral and longitudinal

displacements of the pier. Since the camera cannot

achieve high-power zoom and to ensure a relatively

high actual resolution of the target, the monitoring

distance of this bridge is 2666 mm, the camera focal

length is 24 mm, the pixel size is [not provided in the

original text], and the accuracy is 0.22 mm. As shown

in the following Figure 7, the pixel coordinates of the

target measured by the YOLOV5 - MLR improved

algorithm are (2130.1, 5968.4), and the actual

coordinates in the image plane coordinate system are

(473.22, 1325.89) with the unit of mm.

Real-Time Monitoring of Displacement of Machine Vision Bridge Based on YOLOV5-MLR Study

225

Figure 7: Pixel coordinates and image plane coordinates.

4 CONCLUSION

Bridge safety is a social focus and hot topic.

Therefore, bridges should be regularly monitored and

early-warning systems should be in place to ensure

their normal operation. Existing monitoring methods

mainly rely on coordinate measurement using

measuring equipment. However, the research in this

paper conducts bridge displacement monitoring

through computer vision. Through research, it has

been found that the improved YOLOV5-MLR

algorithm has the following advantages:

(1) In terms of target selection, targets with

relatively complex textures are chosen. The

main advantage of complex-textured targets lies

in the fact that they can be well distinguished

from the surrounding environment. Especially

when there are background images such as

clouds in the detection environment, traditional

black-and-white targets are prone to recognition

errors during the identification process.

Therefore, choosing relatively complex targets

helps to improve the accuracy of target detection.

(2) Compared with previous corner detection

algorithms, the improved YOLOV5-MLR

algorithm takes advantage of the YOLOV5

algorithm. YOLOV5 can quickly and

preliminarily locate the center of the target, and

has a higher detection efficiency. Moreover, as

the target texture becomes complex while

ensuring recognition accuracy, there are many

corner points in complex-textured targets. As a

result, using corner detection algorithms will

return multiple results, and the detection results

are not unique. However, the improved

YOLOV5-MLR algorithm can identify the

center of the target with a unique result, which

is more helpful for quickly extracting the center

point of the target.

(3) In terms of the recognition accuracy of the target

center, it is more precise than both the YOLOV5

and corner detection algorithms. Especially

when the target image is affected by factors such

as illumination and distance, the results obtained

by corner detection are not the center of the

target, with an error of several pixels. When the

improved YOLOV5-MLR algorithm is used for

target center detection, the error can be

controlled within the size of one pixel. Its

accuracy is more conducive to bridge

displacement monitoring and meets the

requirements of displacement monitoring

specifications. In addition, to improve the

adaptability of target center detection, in the

future, high-resolution zoom cameras can be

used for long-distance target center detection, so

as to achieve long-distance bridge displacement

monitoring.

ACKNOWLEDGMENTS

This work had been supported by Basic Research

Project of Guizhou Provincial Department of Science

and Technology, China (Grant No. ZK [2021]-290);

Science and Technology Plan Project of Guiyang

City, China (Grant No. [2024]-1-7); Soft Science

Research Project of Qingzhen City, China (Grant No.

[2023]04); Science and Technology Project of

Guizhou Provincial Department of Transport, China

(Grant No. 2023-123-036); Guizhou Province

Science and Technology Plan Project, China (Grant

No. GZSTCPT-CXTD[2021]008); Funding for

scientific research of Guizhou Communications

Polytechnic University (Grant No. KYQD2022006);

Key Laboratory of High Performance Restoration

Materials for Higher Education Construction Projects

in Guizhou Province, China (Grant No. [2023]030).

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

226

REFERENCES

Liu, L., Luo, S., 2024. Data processing in the application of

bridge deflection deformation [J]. Science and

Technology Innovation, (08): 91-94.

Liao, X., He, Q., Luo, Q., 2024. Application of measuring

robot in bridge static load test [J]. Fujian Building

Materials, (02): 30-32.

Shan, J., Qi, L., 2024. Bridge structural displacement

reconstruction method based on the adaptive Kalman

filter GNSS-RTK fused with acceleration data [J].

Journal of Test Technology, 38(03): 221-229.

Liu, Y., Li, Y., 2024. Adaptive FAST corner point

detection optimization algorithm based on gray scale

mean [J]. Electro-optic and Control, 31(02): 65-71+91.

Shang, M., Wang, K., 2024. Image registration algorithm

based on multiscale Harris angular point detection[J].

Electro-optic and control, 31(01): 28-32.

Bao, J., Sun, D., Huang, J., et al., 2024. FAST detection

algorithm based on adaptive threshold [J/OL]. Journal

of Shanghai Jiao Tong University, 1-25 [2024-07-30].

https://doi.org/10.16183/j.cnki.jsjtu.2023.276.

Busca, G., Cigada, A., Mazzoleni, P., et al., 2014. Vibration

Monitoring of Multiple Bridge Points by Means of a

Unique Vision-Based Measuring System [J].

Experimental Mechanics, 54(2):255-271.

Shang, S., Cao, J., Wang, M., et al., 2024. Research on

corner detection algorithms in machine vision [J].

Computer Measurement and Control, 32(1): 217-225.

Xiang, Y., 2010. Research on image registration

technology based on point features[D]. Shengyang:

Northeastem University.

Lin, P., Li, L., Li, C., 2010. An improved fast SUSAN

corner detection algorithm[J]. Computer and

Modernization, 1(2): 66-68.

Ding, Y., Wang, J., Qiu, Y., et al., 2013. FAST feature

point extraction algorithm based on adaptive

threshold[J]. Command and Controll&Simulation,

35(2): 47-53.

Lee, J.J., Ho, H.N., Lee, J.H., 2012. A Vision-Based

Dynamic Rotational AngleMeasurement System for

Large Civil Structures [J]. Sensors,MolecularDiversity

Preservation International, 12(6): 7326-7336.

Hu, J., Zhu, Q., Zhang, Q., 2022. Global Vibration Comfort

Evaluation of Footbridges Based on Computer

Vision[J]. Sensors, 22(18): 7077.

Zhou, X., Wang, X., Liu, Y., et al., 2023. Method of

vertical displacement measurement based on the

YOLOv5 target detection model and vision [J].

Geospatial Information, 21(12): 25-28.

Real-Time Monitoring of Displacement of Machine Vision Bridge Based on YOLOV5-MLR Study

227