Study on the Influence of Water Stop Failure on Seepage

Characteristics of High Concrete Face Rockfill Dam

Shengjie Di

1,* a

, Jing Liu

and Jiaqi Xu

Northwest Engineering Corporation Limited, Power China, Xi'an, Shaanxi, 710065, China

Hohai University, Nanjing, Jiangsu, 210098, China

Keywords: Concrete Face Rockfill Dam, Osmotic Stability, Stop Water Damage.

Abstract: Aiming at the problem of seepage stability of concrete face rockfill dam, this paper combines the

independently developed Northwest Hydropower Earth-rock Dam Seepage Calculation Platform to carry out

finite element calculation and analysis on the influence of water stop failure on seepage characteristics of dam

body under different schemes. The results show that when the water stop of the panel joint is completely

invalid, the parameters such as water level seepage in the dam body are significantly increased compared with

the complete water stop of the panel joint. The failure water head distribution in the middle of the panel joint

is close to that of the middle and high failure, indicating that the middle failure is more dangerous than the

failure of the higher and lower positions of the panel joint.

1 INTRODUCTION

As a new type of earth-rock dam developed in recent

decades, concrete face rockfill dam has been

recognized by scholars at home and abroad because

of its good safety, wide adaptability, convenient

construction and local materials, and has been widely

used in water conservancy and hydropower projects

at home and abroad (

Chen et al., 2011). According

to the actual operation state of a large number of face

rockfill dams that have been built, the seepage

stability problem is prominent due to the panel

rupture, joint opening and water stop failure caused

by dam deformation and uneven settlement, which

affects the normal operation of the project and even

affects the dam safety or dam failure (

Pan et al.,

2008

). This phenomenon is more obvious for high

dams. Therefore, seepage stability analysis is of great

significance for the long-term safe and stable

operation of CFRD (Xiong

et al., 2015; Lin et al.,

2012; Shakya et al., 2019).

With the development of modern computing

technology and the powerful computing power of

computer, numerical simulation method has become

https://orcid.org/

0009-0003-2095-6560

one of the important methods for seepage stability

analysis of concrete faced rockfill dam. In this paper,

the influence of concrete panel water-stop joint

failure on the seepage characteristics of dam body is

studied by using the Northwest Hydropower-rock

Dam Seepage Calculation Platform (NWHDSCP)

developed by the author 's project team, which

provides a basis for evaluating the safety and stability

of dam body and structural design and optimization

design.

2 BASIC THEORY OF

SATURATED-UNSATURATED

SEEPAGE

The basic differential equation of unsaturated

seepage is derived by the same method as saturated

seepage under the assumption that Darcy 's law is also

applicable to unsaturated seepage. The basic

differential equation of unsteady saturated-

unsaturated seepage is as follows:

208

Di, S., Liu, J., Xu and J.

Study on the Inﬂuence of Water Stop Failure on Seepage Characteristics of High Concrete Face Rockﬁll Dam.

DOI: 10.5220/0013627800004671

In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 208-212

ISBN: 978-989-758-764-1; ISSN: 3051-701X

()

() ()

ij r c i r c c s

kk h k k h Q C h S

xx t



∂∂

∂

+−= + 





∂∂ ∂





(1)

where,

is pressure head.

is saturated

permeability coefficient tensor.

is the permeability

coefficient value in the saturated permeability

coefficient tensor is only related to the third

coordinate axis.

is relative water permeability.

moisture capacity.

is Saturated-unsaturated

selection constant.

is elastic specific storage. Q is

source term.

Considering rainfall infiltration, the definite

conditions of the unsteady saturated-unsaturated

seepage differential equation include initial

conditions and boundary conditions, which are

briefly described as follows:

() ( )

3,2,1,,0,

== itxhxh

icic

(2)

() ()

txhtxh

icic

(3)

() ()

ij r c i r c i n

kk h k k h n q



∂

−+ =



∂





(4)

() () 0

ij r c i r c i

kk h k k h n



∂

−+ ≥



∂





(5)

()

() ()

ij r c i r c i r

kk h k k h n q t



∂

−+ =



∂





(6)

where,

is outer normal direction cosine of

boundary surface.

is initial time.

is known water

head.

is known flow.

()

is rainfall infiltration

flow.

is deterministic hydraulic head boundary.

is known flow boundary.

is rainfall infiltration

boundary.

is saturated escape surface boundary.

Taking the earth dam as an example, the

schematic diagram of the seepage boundary

conditions in Figure 1.

Figure 1: The schematic diagram of seepage boundary.

3 SIMULATION PROCESS

NWHDSCP is developed based on Intel Visual

Fortran, and its process includes three parts : pre-

processing, calculation and post-processing. The

process diagram is shown in Figure 2.

The pre-processing section includes grid file

IIIN.dat, constraint file IIID.dat, material file

IMAT.dat, earth-rock dam calculation preparation

file FILESET.dat and seepage calculation process file

ISEEP.dat. In the calculation plate, the finite element

calculation principle, convergence criterion and

boundary condition processing method are used to

calculate and analyze the files that have been

generated in the pre-processing plate. The platform

has a perfect post-processing interface. The results

show that the results are closely combined with the

needs of engineers. In addition to the basic

displacement and stress cloud diagram, it also

includes parameters closely concerned in engineering

such as seepage flow of different materials and

settlement velocity of soil filling.

Figure 2: NWHDSCP Simulation process.

4 RESEARCH SCHEME AND

ANALYSIS MODEL

4.1 Research Scheme

The project is a concrete face rockfill dam. The

elevation of the foundation surface is 3711.50 m, the

elevation of the dam crest is 3900.50 m, the width of

the dam crest is 10.0 m, the total length of the dam

Study on the Inﬂuence of Water Stop Failure on Seepage Characteristics of High Concrete Face Rockﬁll Dam

209

crest is 510.0 m, and the maximum dam height is

189.0 m. The slope ratio of the upstream dam slope

is 1:1.4, and the cover weight area and the upstream

cover area are set at the elevation of 3797.00 m. The

slope ratio of the downstream dam slope is 1: 1.5

above the elevation of 3848.50 m, and 1:1.4 below

the elevation of 3848.5. The calculation condition

adopts the normal storage level condition, the

upstream water level is 3892.00 m, and the

downstream water level is 3721.81 m. The dam body

partition and typical section diagram are shown in

Figure 3. The research scheme are as flollws.

Scheme 1(S-1): The waterstop system is in good

condition.

Scheme 2(S-2): All panel joints fail.

Scheme 3(S-3): The local failure of the panel joint

is 5m long, which is located at the dam height of 5m,

100m and 180m.

Scheme 4(S-4): The local failure of the panel joint

is 5 m long, which is located at 180 m high of the

dam.

Scheme 5(S-5): The local failure of the panel joint

is 5 m long, which is located at 100 m high of the

dam.

Scheme 6(S-6): The local failure of the panel joint

is 5 m long, which is located at 5 m high of the dam.

Figure 3: Computed profile diagram.

4.2 Analyze the Model and Parameters

The typical calculation section diagram of the upper

section is simplified, and the three-dimensional

model is established and meshed by NWHDSCP.A

total of 5 panels ( single width 12m ) are established.

The length of the model is 2307m, of which the

length above the dam axis is 1152m, and the dam axis

is 1155m below the dam axis. The bottom elevation

of the model is taken to 2918.5m elevation, and the

depth of the intercepted dam foundation is about 4

times the maximum dam height, which meets the

requirements of finite element calculation. The model

is divided into 488900 mesh elements and 518271

nodes. The three-dimensional model and grid

diagram are shown in Figure 4 and Table 1.

Figure 4: Finite element analysis model.

Table 1: permeability coefficient of each material area.

Material

Permeability

coefficient（cm/s

）

Allowable

hydraulic slope

of landside

Concrete slab

1.00×10

-7

200.00

Bedding cushion

(2A)

5.83×10

-4

0.25

Transition zone

(

)

5.39×10

-4

0.20

Upstream rockfill

area (3B)

2.14×10

-2

Downstream

rockfill area (3C)

2.07×10

-3

Impervious blanket

(

)

1.00×10

-5

Drainage district

(

)

5.00×10

-1

4.3 Hydraulic Gradient of Each

Material Partition

According to the flow velocity value of each material

partition, the maximum hydraulic gradient of each

calculation scheme is calculated, and the analysis

results are shown in Table 2. It can be seen from the

table that when the local water stop failure occurs in

the face joint, the cushion and the transition material

play a certain role in retaining water, and the

maximum hydraulic gradient value increases

significantly. The maximum gradient of the cushion

and the transition material is 3.8 and 0.8; when all the

water-stop joints fail, the anti-seepage ability of the

cushion and the transition material is insufficient, the

water level line inside the dam body rises obviously,

the maximum hydraulic gradient value is greater than

the local failure, and the maximum gradient of the

cushion and the transition material is 14.86 and 2.27.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

210

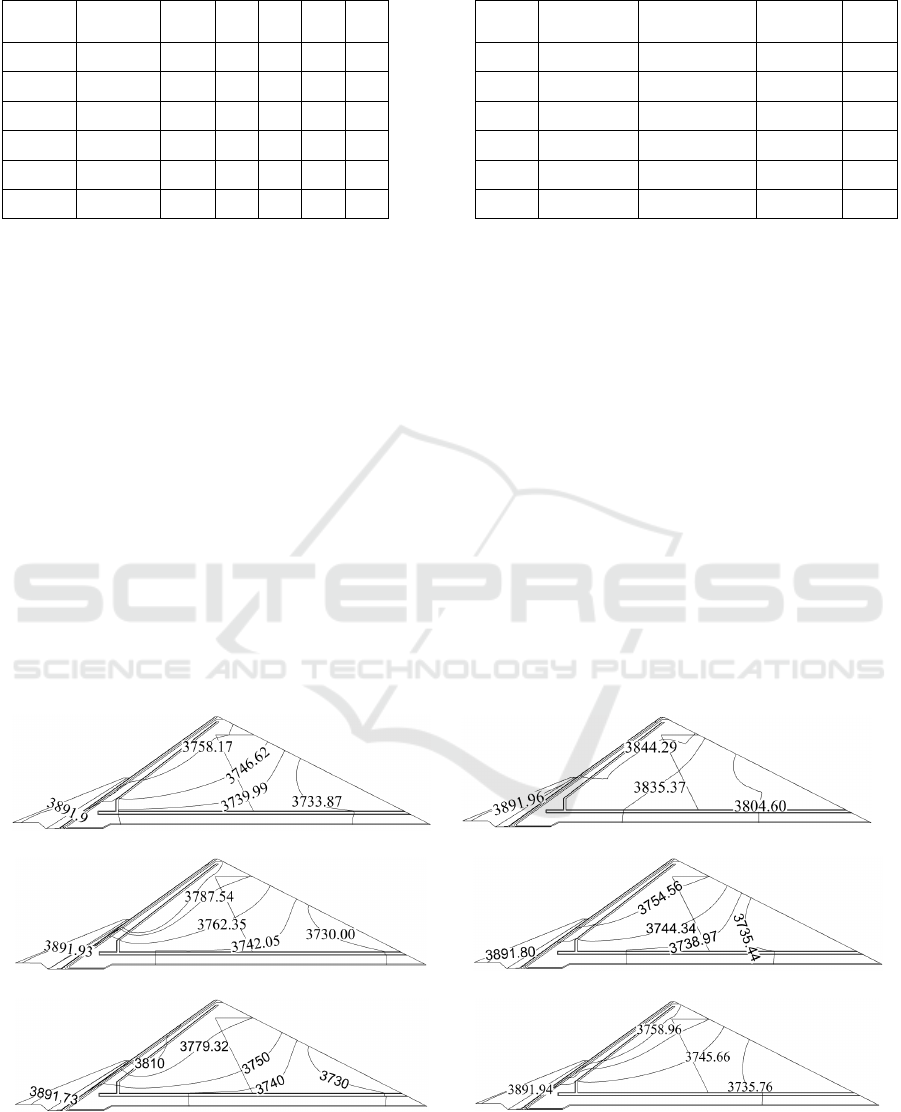
Table 2: Permeability coefficient of each material area.

Scheme

Concrete

slab

2A 3A 3B 3C 3D

S-1 150.60

0.03 0.02 0.04 / 0.07

S-2 34.20

14.86 2.27 0.05 0.18 0.09

S-3 146.80

3.81 0.81 0.04 / 0.52

S-4 150.60

0.03 0.03 0.04 / 0.10

S-5 149.10

2.93 0.65 0.04 / 0.42

S-6 149.40

0.03 0.03 0.04 / 0.11

4.4 Seepage Flow in Each Partition

The calculation section of seepage flow is divided

into three sections : dam body, anti-seepage curtain

and bedrock. The seepage flow of each partition

under each calculation scheme of concrete face

rockfill dam is shown in Table 3. It can be seen from

the table that when all the panel joints fail, the

seepage flow through the dam increases sharply, and

is significantly higher than the local failure. When the

water stop at the bottom of the panel joint fails, the

seepage flow through the dam body is significantly

lower than that in the middle and high parts. The main

reason is that the cover and cover weight on the

upstream side of the dam body play a certain anti-

seepage role, and the water stop failure of the panel

joint has little effect on the seepage flow of the anti-

seepage curtain and bedrock in Figure 5.

Table 3: Permeability coefficient of each material area.

Scheme

Concrete

slab

Impervious

curtain

Bed rock Total

S-1 0.5 12.5 2.9 15.9

S-2 1548.0 11.7 2.8 1562.5

S-3 323.1 10.4 2.6 336.1

S-4 104.3 12.5 2.9 119.7

S-5 317.3 10.4 2.6 330.3

S-6 10.2 12.5 2.9 25.6

4.5 Analysis of Dam Head

When the panel joint is used normally, the water head

in the dam body is significantly reduced, and the anti-

seepage effect of the panel is obvious. When all the

panel joints fail, the water head in the dam body is

large and decreases slowly along the flow direction;

when the height of the panel joint fails, the water head

is dense near the failure position, and the water head

in the dam body is higher in the upstream rockfill area,

but it decreases rapidly along the flow direction. The

distribution of failure water head in the middle of the

panel joint is close to that of the middle and high

failure, which indicates that the middle failure is

more dangerous than the higher position of the panel

joint and the lower position of the upstream

blanketing effect. When the water stop at the bottom

of the panel joint fails, it has little effect on the water

head in the dam body.

(a) S-1. (b) S-2.

(e) S-5. (f) S-6.

Figure 5: Equal water head isoline map.

Study on the Inﬂuence of Water Stop Failure on Seepage Characteristics of High Concrete Face Rockﬁll Dam

211

5 CONCLUSION

When all the water stops of the panel joints fail, the

water level line in the dam body rises obviously,

which is much higher than the action range of the

drainage body. There is also a saturated zone in the

downstream rockfill area, and the seepage flow

through the dam body increases sharply. The

maximum slope of the cushion and the transition

material reaches 14.86 and 2.27.

When the height and height of the face slab joint

fail, the water level in the dam body increases

significantly in the upstream rockfill area, but soon

decreases to the range of the drainage body, and the

maximum slope of the cushion and transition material

is 3.8 and 0.8 ; the distribution of failure water head

in the middle of the panel joint is close to that of the

middle and high failure, indicating that the middle

failure phase is more dangerous than the higher

position of the panel joint and the lower position of

the upstream blanketing effect.

ACKNOWLEDGMENTS

This work was financially supported by the National

Key Research and Development Program of China of

Northwest Engineering Corporation Limited, Power

China. In the meantime, we express thanks to our

colleagues for their help and technical support.

REFERENCES

Chen, S.K, Yan, J, Li, J.M., 2011. Seepage field 3D finite

element simulation of concrete faced rockfill dam

under failure condition of vertical fracture. Rock and

Soil Mechanics, (11): 3473-3478.

Pan, S.H, Mao, X.Y., 2008. Seepage field finite element

simulation of faced rockfill dam under cases of vertical

joints and seal failure. Rock and Soil Mechanics,

29(S1): 145-148.

Xiong, L, Dang, F.N, Zhang, H.F., 2015. Seepage field

analysis of a concrete face rockfill dam after water stop

failure. Water Resources and Power, 33(06): 80-83.

Lin, Q.M, Gong, J., 2012. Analysis of influence of panel

cracking on seepage characteristics of concrete face

rockfill dam. Jilin Water Resources, (10): 1-4.

Shakya, C, Luo, X.Q., 2019. Coupling Internal Erosion

through Concrete Face Rockfill Dams with Damage in

Face Slab under Impounding. Journal of Physics:

Conference Series, 1176(5): 052067(13app).

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

212