Analysis of Soil Pressure Distribution and Fracture Surface Inside

Mechanically Stabilized Earth (MSE) Walls of High-Speed Railways

Guangpeng Liu

1,2,3,* a

, Nan Zhang

2,3

, Guoliang Shi

2,3

, Weiming Huang

2,3

and Hong Xiao

School of Civil Engineering, Sun Yat-sen University, Guangzhou 510275, China

Guangzhou Construction Group Co., Ltd, Guangzhou 510030, China

Guangzhou Municipal Group Design Institute Co., Ltd, Guangzhou 510060, China

School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China

Keywords: MSE Wall, Model Test, Soil Pressure, High-Speed Railway, Fracture Surface.

Abstract: Due to the extremely strict settlement requirements for the high-speed railways, the MSE wall, as an

environmentally friendly structure, the variation of the soil pressure and the fracture surface are related to the

accurate design of the wall. Three sets of model tests were designed based on the similar theory, and the soil

pressure changes in the MSE wall and the retaining wall panel under different loads were studied respectively.

At the same time, the high-speed train-track-MSE wall model was conducted to analyze the dynamic loading

effect, the distribution of soil pressure and the changes of fracture surface. The result shows that: increasing

the layers of ribs and increasing the length of ribs will reduce the soil pressure. Under static load, the soil

pressure inside the MSE wall increases linearly along the wall height, while under the train load, the soil

pressure increases linearly in the stable area and increases non-linearly in the active area. In the designing,

the fracture surface of the MSE wall is considered to be a fixed value. However, if the failure of the ribs in

the range of 0.15H~0.25H at the bottom of the wall occurs, the position of the fracture surface will move

upward along the wall. The guidelines suggest when designing the high-speed rail MSE walls, 0.15H~0.25H

range should be strengthened.

1 INTRODUCTION

MSE wall is composed of reinforcement ribs, wall

panels, and connecting parts. Due to its outstanding

advantages such as less land occupation, low cost,

and easy construction, it has been widely used in

railway infrastructure.

Many scholars have also conducted a large

amount of theoretical and experimental research. Jean

et al. (Jiang et al., 2016; Noike et al., 2004; Jean et al.,

2015; Alain et al., 2017) combined full-scale model

tests with finite element simulation calculations to

simulate train loads using harmonic loads, and

calculated the mechanical characteristics of MSE

walls. Fei et al. (2018) used a combination of

centrifugal testing and finite element strength

reduction method to study the fracture surface forms

of MSE walls with different step forms. Ehsan et al.

(2018) regarded the MSE wall as a two-phase

medium material and calculated the form of the

https://orcid.org/0000-0002-3711-7902

fracture surface. Mohammad et al. (2018) used a

combination of experimental and numerical

simulation methods to study the deformation and soil

pressure changes of MSE walls under different

external loads.

Xiao et al. (2021) monitored the horizontal

displacement, soil pressure, and potential sliding

surface of the wall through large-scale indoor model

tests of a two-step MSE wall, and analyzed the

evolution law of the stepped MSE wall fracture

surface. Wang et al. (2023) conducted indoor model

tests to analyze the changes in mechanical behavior

of MSE walls, such as settlement, horizontal

displacement of panels, lateral soil pressure

coefficient, and grid strain. Ren et al. (2021)

conducted indoor model tests on MSE walls under

horizontal static dynamic loads, exploring the

deformation, horizontal soil pressure, reinforcement

strain, and potential fracture surface of the retaining

walls. Xu et al. (2023) used model calculations to

Liu, G., Zhang, N., Shi, G., Huang, W., Xiao and H.

Analysis of Soil Pressure Distribution and Fracture Surface Inside Mechanically Stabilized Earth (MSE) Walls of High-Speed Railways.

DOI: 10.5220/0013626300004671

In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 173-182

ISBN: 978-989-758-764-1; ISSN: 3051-701X

173

study the variation law of the bearing capacity of

retaining walls under strip loads. Yang et al. (2021)

analyzed the evolution law of vertical stress, geogrid

strain, and settlement of the foundation and wall

during construction and after construction through

on-site in-situ tests of railway retaining walls.

From the above research, it can be seen that most

scholars currently focus on static load testing and

theoretical research, while some scholars mainly use

harmonic loads to replace train loads. However, there

is no specific design for MSE walls for high-speed

railways in the existing railway design rules. In order

to further study the soil pressure, fracture surface

changes, and stability characteristics of MSE walls

for high-speed railways under static and dynamic

loads, a model test of the retaining wall was first

carried out. Then, a dynamic coupling model of the

MSE wall for high-speed railways was established

based on finite element analysis. The changes in soil

pressure and reinforcement stress of the retaining wall

under vehicle loads were calculated. Based on the

failure of reinforcement materials, the change law of

the fracture surface inside the retaining wall was

calculated. Relevant research can provide data

support for the accurate designing of MSE walls for

high-speed railways in the future.

2 MODEL TEST

2.1 Experimental

The experiment in this article is based on an intercity

railway MSE wall. The MSE wall has a height of

7.8m, and the wall panels are made of C30 concrete

with a size of

0.5 0.3 0.3mmm××

. The geogrid is

unidirectional made of high-density polyethylene

material, whose length is

8.0 ~ 10.5m .

2.2 Model Similarity Relationship

The similarity theorem (Du et al., 2018; TB 10621-

2014) was used to calculate the model geometric

similarity, and the geometric similarity constant

=10

, strain similarity constant

1/10C

, soil

density similarity ratio

, soil elastic modulus

similarity

C =

, and tensile modulus similarity

constant of the reinforcement

=10

. According to

the similarity

law, the similarity relationship of

the other parameters is calculated as follows: stress

similarity ratio

CCC

σγ

, bulk density

similarity ratio

1/10C

, and Poisson's ratio

similarity

=1C

2.3 Similar Materials

The model experiment takes sand as the filler, with an

optimal moisture content 11%, compaction degree

0.94, and dry density 1.85g/cm

. When the optimal

moisture content is reached, the density of sand is

2.04g/cm

The wall adopts modular facing panels,

considering the convenience of production and

assembly. In the experiment, wood panels can meet

the relevant requirements.

This model experiment uses a unidirectional

tensile geogrid as the ribs, with a nominal tensile

strength ≥ 25kN/m. Other physical and mechanical

properties are shown in Table 1.

2.4 Test Design

Three sides of the model box are made of 1.5cm thick

tempered glass, and the wall is composed of a wooden

board with dimensions

533cm cm cm××

(length

5cm width 3cm height 3cm) connected as a whole

using steels. Set up horizontal barriers at the bottom

of the wall to simulate the limiting effect of the

foundation on the wall bottom.

The size of the model box is determined by the

geometric similarity relationship (length x width x

height), with a filling height of 0.78m. It is filled in

layers and compacted.

Set up a plate in the middle of the wall and use a

pressure sensor to control the jack to accurately

loading. According to the railway design

specifications, the maximum designing load on the

top of the track foundation is 54.1kPa. At the same

time, in order to study the variation of the wall under

different loads, step-by-step loading is adopted.

When using a jack for loading in the experiment,

the magnitude of the applied load is determined

through a pressure sensor, and the magnitude and

variation of the loading force are recorded and

controlled through an IMC data acquisition

instrument. The method of burying soil pressure

boxes inside the wall is adopted to measure the soil

pressure. The test site is shown in Figure 1.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

174

Table 1: Geogrid physical parameters.

nominal tensile

strength (kN/m)

elongation at

yield (%)

Tensile force at

2% elongation

(kN/m)

Tensile strength

at 5% elongation

(kN/m)

The spacing

between individual

tendons(mm)

Thickness of

single rib (mm)

≥25 ≤10 ≥7 ≥14 30 1

Figure 1: Test model.

Due to the fact that the spacing and length of ribs

are the main factors in the design of MSE walls (Yang,

2015), three sets of different spacing and length of

ribs were tested under different cases. The spacing

and length of ribs in each set of tests are shown in

Table 2.

Table 2: Test case.

case

Number of ribs

layers

ribs spacing

ribs length

1 7 0.1 0.8

2 5 0.15 0.8

3 5 0.15 1

3 RESULTS AND DISCUSSION

3.1 Soil Pressure on Retaining Wall

Under static load, tests were conducted on the

horizontal soil pressure of MSE walls at different

heights. The comparison of horizontal soil pressure

on the walls with different ribs layers is shown in

Figure 2(a), and the comparison of soil pressure with

different ribs lengths is shown in Figure 2(b).

0.51.01.52.02.5

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

Distance from the retaining wall(m)

Wall soil pressure(kPa)

0.1m-10kPa 0.1m-30kPa 0.1m-54.1kPa

0.15m-10kPa 0.15m-30kPa 0.15m-54.1kPa

0.8

0.0

0.10m

0.15m

wall soil

0.5 1.0 1.5 2.0 2.5

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

Distance from the retaining wall(m)

Soil pressure(kPa)

0.8m-10kPa 0.8m-30kPa 0.8m-54.1kPa

1m-10kPa 1m-30kPa 1m-54.1kPa

0.8

0.0

0.8m

1.0m

wall soil

(a) Comparison of spacing between different reinforcement

materials

(b) Comparison of different reinforcement lengths

Figure 2: Distribution of soil pressure with burial depth under static load.

Overall, the horizontal soil pressure on the wall

shows a non-linear and gradually increasing trend in

the vertical direction. From the different spacing of

ribs in Figure 2(a), it can be seen that the soil pressure

in case 2 is higher than that in case 1, indicating that

increasing the number of ribs layers and reducing the

vertical spacing of ribs can effectively reduce the

distribution of soil pressure.

From Figure 2(b), it can be seen that overall, the

soil pressure at the bottom under case 2 is higher than

that under case 3, indicating that increasing the length

of the ribs can effectively reduce the distribution of

soil pressure.

Analysis of Soil Pressure Distribution and Fracture Surface Inside Mechanically Stabilized Earth (MSE) Walls of High-Speed Railways

175

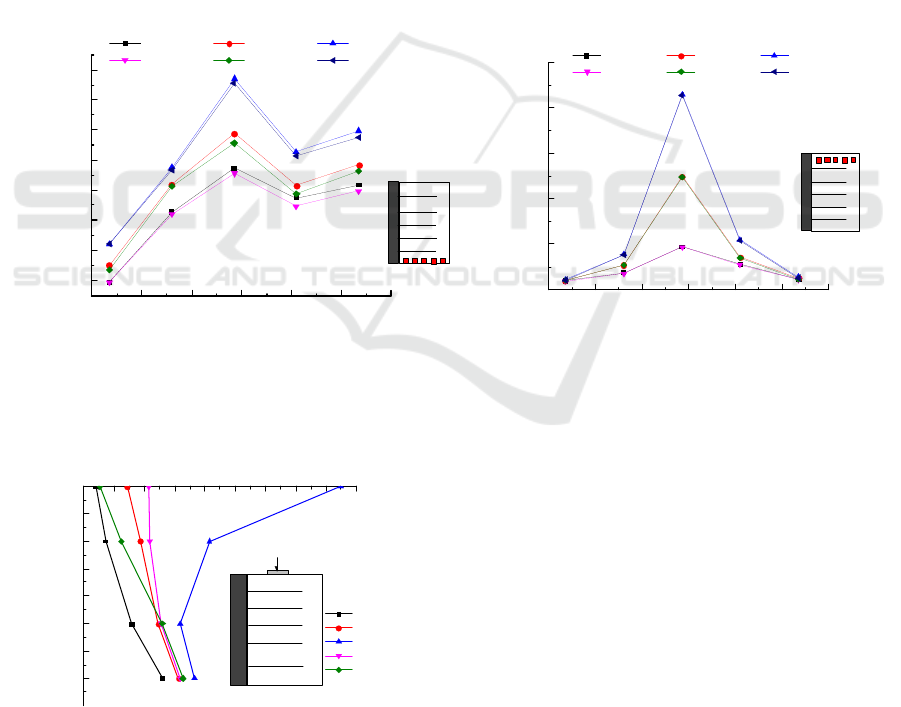
3.2 Vertical Soil Pressure inside the

MSE Wall

In the case where the number of ribs layers is the same

and all ribs are buried in the same position, the

influence of different ribs lengths on the vertical soil

pressure inside the was studied. The comparison of

experimental data for conditions 2 and 3 is shown in

Figure 3.

Under static load, the vertical soil pressure inside

the wall exhibits a non-linear distribution along the

length of the ribs, with the maximum soil pressure

occurring near the loading position and smaller at

ends. This is mainly because near the wall, due to the

horizontal displacement of the wall, soil pressure near

the wall is released. The soil on the side far away from

the load position is less affected by external loads.

From Figure 3(a), it can be seen that the length of

the ribs has a significant impact on the soil pressure

at the bottom of the wall. The soil pressure in case 2

is significantly higher than that in case 3. The ribs

increased from 0.8m to 1m, and the maximum soil

pressure at the bottom decreased by an average of

0.25KPa, about 1.4%. In Figure 3(b), the maximum

soil pressure at the bottom end decreased by an

average of 0.17 KPa, approximately 1.1%. In Figure

3 the maximum soil pressure at the bottom decreased

by an average of 0.08KPa, approximately 0.5%. The

length of the ribs in Figure 3 has little effect on the

soil pressure value at the top of the wall. The

influence of the length of the ribs on the soil pressure

inside the wall gradually weakens from the bottom to

the top.

To analyze the variation of soil pressure along the

height of the wall, the data of soil pressure along the

height of the wall at distances of 0.07m, 0.32m,

0.57m, 0.82m, and 1.07m are shown in Figure 4.

0.00.20.40.60.81.01.2

Vertical soil pressure(kPa)

Distance from the retaining wall(m)

0.8m-10kPa 0.8m-30kPa 0.8m-54.1kPa

1m-10kPa 1m-30kPa 1m-54.1kPa

wall

0.0 1.2

soil

0.0 0.2 0.4 0.6 0.8 1.0 1.2

Vertical soil pressure(kPa)

Distance from the retaining wall(m)

0.8m-10kPa 0.8m-30kPa 0.8m-54.1kPa

1m-10kPa 1m-30kPa 1m-54.1kPa

wall

0.0

1.2

soil

(a) Vertical soil pressure on the first layer (at the bottom of

the retainin

wall

)

(b) Vertical soil pressure on the fourth layer at the top of

the wall

Figure 3: Distribution of vertical soil pressure along the reinforcement under static load.

5 10 15202530354045

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

1.070.57

0.7 8

load

Wall height(m)

Vertical soil pressure(kPa)

0. 07m

0. 32m

0. 57m

0. 82m

1. 07m

wall

Figure 4: Distribution of vertical soil pressure inside the

retaining wall under static load.

From the Figure 4, it can be concluded that except

for the 0.57m below the loading position, the soil

pressure inside the wall at all other positions

increases linearly with the height, which is basically

consistent with the law described by Coulomb's soil

pressure. At a height of 0.57m, the soil pressure inside

the wall shows a non-linear trend. This is mainly due

to the energy dissipation of the soil below the wall

under external forces, which continuously decreases

along the depth of the wall. At the same time, there is

a certain increasing trend at the bottom of the wall,

which is because the bottom of the wall is outside the

range of external load influence.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

176

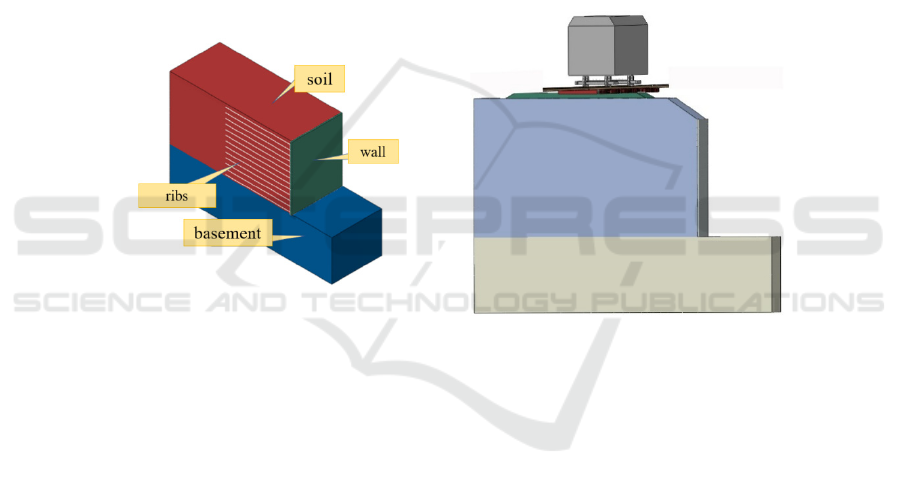
4 NUMERICAL SIMULATION

4.1 Modeling

The subgrade in the model adopts the Mohr Coulomb

constitutive model, and the embedded contact

relationship between the ribs and the soil is adopted.

The model (length x width x height) is 12, 6, 7.8m.

The soil and ribs parameters in the model are based

on the actual material of the intercity railway. The

model established using the finite element software is

shown in Figure 5 (a).

By comparing the static model with the

experimental results, the rationality of the material

and contact relationship can be verified. Furthermore,

the dynamic model can be used to calculate the soil

pressure during high-speed train operation.

In the dynamic model, relevant parameters such

as subgrade and foundation are selected according to

the actual parameters in relevant literature (Zhai,

2007), while parameters related to dynamic models

such as tracks and trains are selected according to the

provisions in literature (TB 10025-2019; Li, et al.

2020). Hertz contact relationship is used between

vehicle and tracks.

In the model, fixed boundary conditions are set at

the bottom of the wall, and displacement boundaries

are applied in the longitudinal and transverse

directions of the model. A binding contact

relationship is adopted between the track bed and the

subgrade, and displacement boundary conditions are

also set at the longitudinal ends of the rail. The three-

dimensional coupling system of vehicle track MSE

wall subgrade is shown in Figure 5(b).

(

)

Static calculation model for MSE walls

(

namic model of vehicle track MSE wall

Figure 5: Dynamic calculation model of MSE wall for high-speed railway.

4.2 Model Validation

In the static calculation model, the same load as the

test is taken as 10kPa, 20kPa, 30kPa, 40kPa, 50kPa,

and 54.1kPa, respectively. The vertical soil pressure

cloud map under static loading is shown in Figure 6

(a), and the comparison between the vertical soil

pressure at the top of the retaining wall and the test

results is shown in Figure 6 (b).

In the calculation, the same load as the test is taken

as 10kPa, 20kPa, 30kPa, 40kPa, 50kPa, and 54.1kPa,

respectively. The vertical soil pressure cloud map of

the MSE wall under static loading is shown in Figure

6 (a), and the comparison between the vertical soil

pressure at the top of the wall and the test results is

shown in Figure 6 (b).

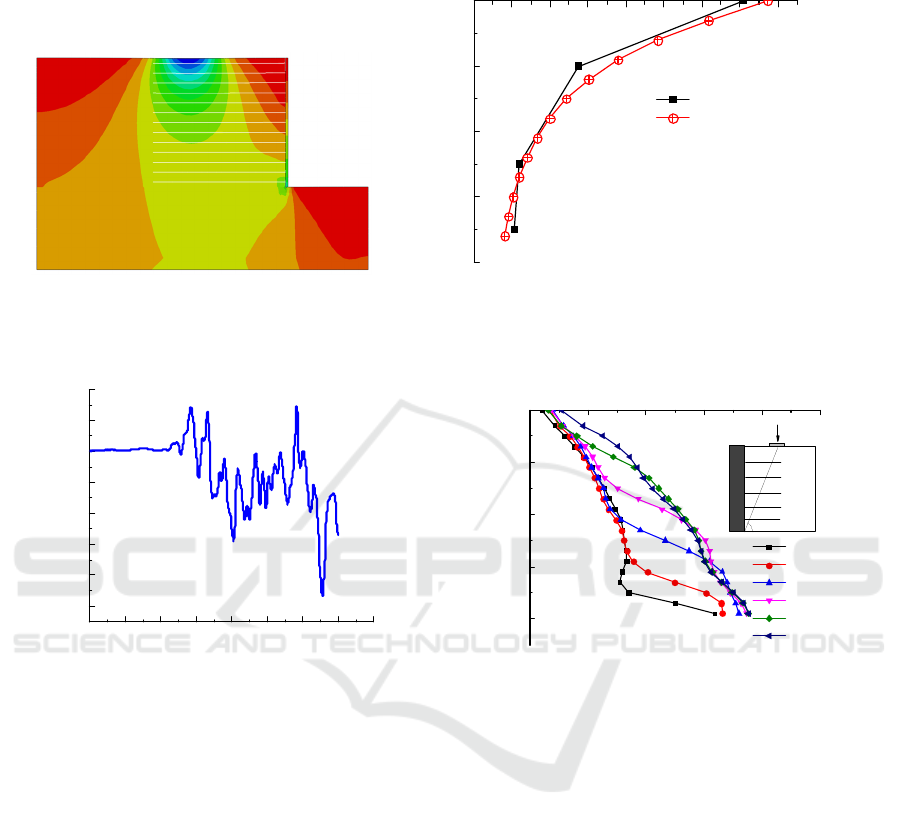
From Figure 7 (a), it can be seen that at around 0.3

seconds, the first bogie of the train passes through the

middle of the wall, and at around 0.6 seconds, the

second bogie of the train passes through the middle

of the wall. When the train bogie passes through the

wall, there are two obvious peaks in the vertical soil

pressure. Compared with static soil pressure, the

dynamic soil pressure under the action of a train has

a clear variation with time. At the same time, when

the train pass through the wall, the soil pressure inside

the wall reaches its maximum.

From Figure 7 (b), it can be concluded that under

the high-speed trains load, the distribution of soil

pressure inside the wall shows a non-linear

distribution in the active zone and a linear distribution

in the stable zone. The soil pressure in the stable zone

is consistent with the law calculated by the Coulomb

soil pressure calculation formula. The distribution of

soil pressure under train load is only the same as that

under static load in the stable zone, but different in

the active zone. Therefore, it is recommended to

comprehensively consider the effects of dynamic and

static loads when calculation.

Analysis of Soil Pressure Distribution and Fracture Surface Inside Mechanically Stabilized Earth (MSE) Walls of High-Speed Railways

177

10 15 20 25 30 35 40 45 50

Wall height(m)

Vertical soil pressure(kPa)

t est result

Simulation results

(a) (b)

Figure 6: Comparison of vertical displacement.

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

7. 0× 10

7. 2× 10

7. 4× 10

7. 6× 10

7. 8× 10

8. 0× 10

8. 2× 10

8. 4× 10

Vertical soil pressure(kPa)

Time(s)

5.0×10

1.0×10

1.5×10

2.0×10

2.5×10

45°+f /2

load

7.8

Distance from the wall bottom (m)

Vertical s oil pressure(kPa)

wall

(a) Changes in dynamic soil pressure inside the wall

during train operation

(b) Distribution of dynamic soil pressure inside retaining

walls under dynamic loading

Figure 7: Vertical soil pressure inside the wall under dynamic load.

4.3 Failure of Ribs Leads to Changes in

the Soil Pressure Zone and

Fracture Surface

When the intercity railway train runs at a speed of

250km/h, the variation of soil pressure at the middle

position of the wall with the train running time is

shown in Figure 7 (a), and the distribution of soil

pressure inside the wall is shown in Figure 7 (b)

It is generally believed that the location of the

fracture surface of MSE walls will not change, and the

stable and active areas of soil pressure distribution are

also unchanged. However, in practical situations, if a

layer of ribs in the MSE wall fails, will the regional

range change, and how will the corresponding

fracture surface change? To study this problem, the

following different working conditions were

calculated separately.

(1) Firstly, the stress-strain and fracture surface

changes were calculated under the condition of no

failure of the reinforcement within the entire range,

as follows:

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

178

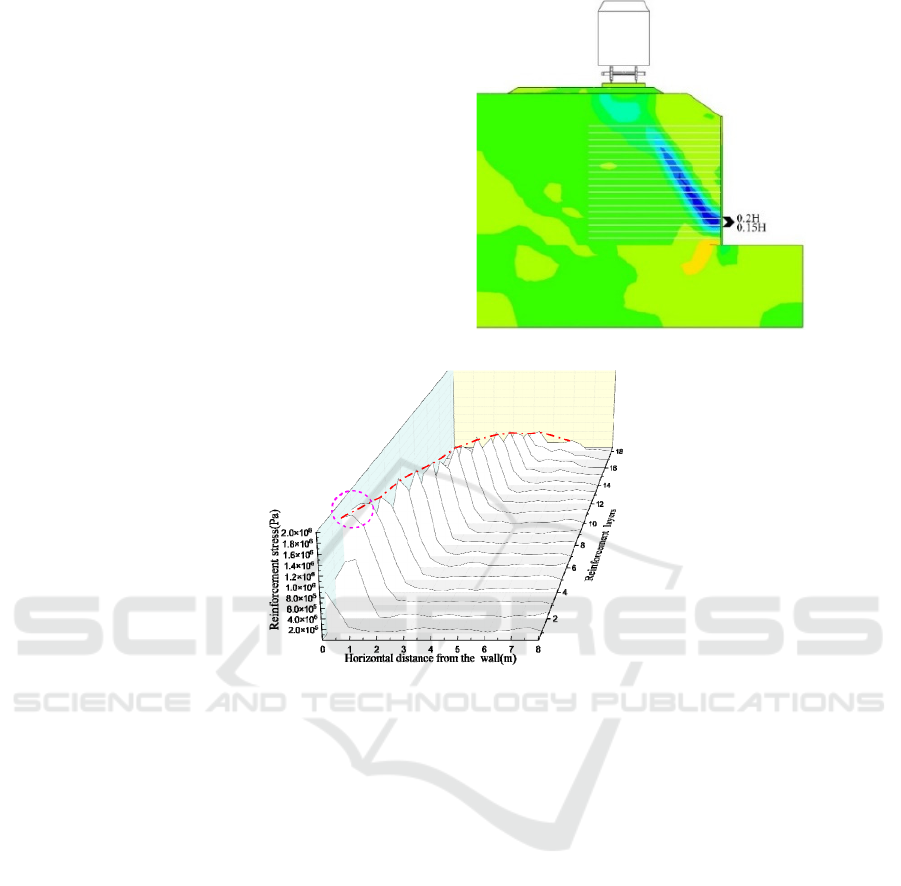
(a) Vertical displacement and strain cloud map of

soil inside the retainin

wall

(b) Vertical strain cloud map of soil

(

)

Stress distribution dia

ram of each la

er of reinforcement stri

Figure 8: Stress distribution of soil and reinforcement strips when the train passes through the retaining wall.

From Figure 8 (a), it can be observed that when

the train passes through the wall, there are two

obvious areas of vertical soil displacement inside the

wall, one is the inclined downward displacement area,

and the other is the inclined upward area at the bottom

of the wall. When the train passes through the wall, a

shear slip zone will inevitably appear between the two

zones. The position the sliding band is 0.15H at the

bottom of the wall.

From Figure 8 (b), it can be seen that when the

train passes through the wall, a significant strain

concentrated shear slip zone appears in the soil, with

the maximum strain concentrated between 0.15H and

0.2H at the bottom end.

From Figure 8 (c), it can be obtained that when the

train passes through the wall, each layer of ribs shows

a significant peak. The location of the fracture surface

of the wall is determined by connecting the maximum

stress of each layer of ribs with a red line. It can be

observed that the maximum stress in the third and

fourth layers of the red circle is significantly higher

than the others, so the most likely to fracture first is

the third and fourth layers.

It can be seen that the maximum reinforcement

stress of the 3rd and 4th layers plays a crucial role in

the entire ribs layer. In order to study how the stress

distribution of the ribs when two or more layers of

ribs fail, and the changes of the shear slip zone and

fracture surface inside the wall, the stress and soil

strain changes of the ribs were studied when the 3rd,

4th, 5th, and 6th layers fail respectively.

(2) When the third layer of ribs fails, the stress

distribution of the ribs inside the retaining wall is

shown in Figure 9.

From Figure 9, it can be got that when the third

layer ribs fail, the maximum stress of the fourth layer

ribs is significantly higher than that of the other layers,

and the maximum stress increases by 54% compared

to the maximum stress without failure. At the same

time, the position of the fracture surface has also

undergone significant changes, from the original

position of the third layer to the fourth layer, as shown

by the red line.

(3) When the fourth layer of ribs fails, the vertical

Analysis of Soil Pressure Distribution and Fracture Surface Inside Mechanically Stabilized Earth (MSE) Walls of High-Speed Railways

179

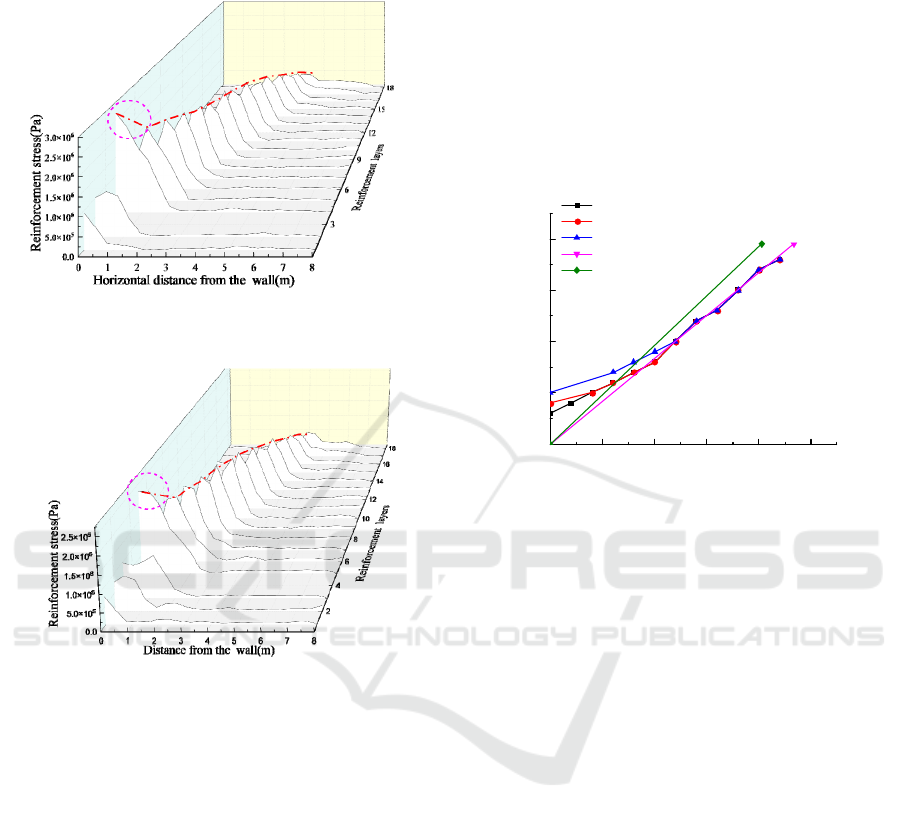
displacement, strain, and stress distribution of the soil

are shown in Figure 10.

Figure 9: Stress distribution of the ribs in the wall during

the third layer fail.

Stress distribution of reinforcement when the fourth

layer of reinforcement fails

Figure 10: Stress distribution of soil and reinforcement

when the fourth reinforcement fails.

From Figure 10, it can be seen that when the train

passes through the wall, there are two obvious areas

of vertical dynamic displacement of the soil inside the

wall. When the train passes through the retaining wall,

a shear slip zone will inevitably appear between the

two displacement zones. The position at the bottom of

the sliding band is 0.2H from the bottom of the wall.

From Figure 10, it can be seen that when the train

passes through the wall, there is a clear sliding slip

zone with concentrated strain inside the wall, and the

maximum strain is concentrated between 0.2H and

0.25H at the bottom end.

From Figure 10, it can be seen that when the fourth

layer’s ribs fail, the maximum stress of the fifth ribs

is significantly higher than that of the other layers, and

the maximum stress increases by 39.7% compared to

the maximum stress when without failure. At the same

time, the position of the fracture surface has also

undergone significant changes, from the third layer to

the fifth layer, as shown by the red line.

Draw the fracture surface positions of the 3rd, 4th,

5th, and 6th layers of the reinforcement ribs when

they fail and all layers have no failure in the same

diagram. At the same time, the Rankine fracture

surface and the railway standard 0.3H fracture

surface are also compared and analyzed in the figure,

as shown in Figure 11.

012345

Stable zone

Distance from the retaining wall(m)

Distance from the bottom of the wall(m)

No failure or failure in layer 5/6

3rd layer reinforcement failure

4th layer reinforcement failure

0.3H fracture surface

Rankine fracture surface

Active area

Figure 11: Comparison of fracture surfaces under different

layers of reinforcement failure.

From the Figure 11, it can be concluded that when

the third layer of ribs fails, the fracture surface of the

MSE wall will rises from the original 0.15H to 0.2H.

When the fourth layer’s ribs fails, the position of the

fracture surface will rises from the original 0.15H to

0.25H. When the fifth or sixth layer’s ribs fail, the

fracture surface returns to the original 0.15H position.

It can be seen that only when the ribs fail within the

range of 0.15H to 0.25H, the position of the fracture

surface inside the MSE wall will change.

By comparing the location of the fracture surface

calculated in this article with the American Rankine

fracture surface and the 0.3H fracture surface, it can

be concluded that the traditional belief is that the

location of the fracture surface is fixed and

unchanging, and the active and stable areas divided

by the fracture surface are also fixed and unchanging.

But if the ribs in the range of 0.15H to 0.25H fails, it

will change. At the same time, the calculation results

of the Rankine fracture surface are relatively small,

while the results of the 0.3H fracture surface are

relatively conservative.

In the designing of MSE walls for high-speed

railways, the ribs at the bottom of the wall should be

strengthened within the range of 0.15H to 0.25H. The

design principle should ensure that the failure of a

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

180

certain layer’s ribs will not cause further failure when

the stress of the previous layer’s increases.

5 CONCLUSION

Model tests were conducted to investigate the soil

pressure changes inside MSE walls under static and

dynamic train loads. A three-dimensional coupled

model of high-speed train track MSE walls was

established, and the soil pressure changes and fracture

surface were analyzed. The conclusions are as follows:

(1) Through static load tests, it has been found that

reducing the spacing and increasing the length of ribs

have a certain effect on reducing the soil pressure.

(2) Under static load, the soil pressure is linearly

distributed along the depth of the wall. However,

under train load, the soil pressure inside the wall is

linearly distributed in the stable zone, but exhibits

nonlinear trend in the active zone. Therefore, when

calculating the soil pressure of the MSE wall, the

effects of train and static loads should be

comprehensively considered.

(3) In existing designs, it is generally believed that

the location of the fracture surface in the active and

stable areas of the MSE wall is fixed and unchanged.

However, when the ribs at the bottom of the wall fails

within the range of 0.15H to 0.25H under the load of

high-speed trains, the fracture surface of the wall will

move upwards along the wall. Therefore, in the design

of high-speed railway MSE walls, it is recommended

to strengthen the designing of the ribs at the bottom

of the retaining wall within the range of 0.15H to

0.25H.

ACKNOWLEDGMENTS

This research was funded by the Guangzhou

Construction Group Technology Plan Project (Grant

no. [2022]-KJ005, [2023]-KJ013, [2023]-KJ014,

[2024]-KJ043, [2024]-KJ106, [2024]-KJ105)

REFERENCES

Jiang, Z. W., Guo, X. Y., Li, W. T., et al. 2016. Self-

shrinkage behaviors of waste paper fiber reinforced

cement paste considering its self-curing effect at early-

ages. International Journal of Polymer Science, 2016:

1-12.

Noike, T., Goo, I. S., Matsumoto, H., et al. 2004.

Development of a new type of anaerobic digestion

process equipped with the function of nitrogen removal.

Water Science & Technology, 49(5/6): 173-179.

Jean, B. P., Alain, C., Emmanuel, B., et al. 2015. Dynamic

behavior of a mechanically stabilized earth wall under

harmonic loading: experimental characterization and

3D finite elements model. Computers and Geotechnics,

65: 199-211.

Alain, C., Emmanuel, B., Jean, B. P., et al. 2017. Numerical

simulation of the response of a reinforced wall to a high

speed train passage. International Journal for

Numerical and Analytical Methods in Geomechanics,

41(11): 1285 -1303.

Fei, S., Liu, H. B., Ma, L. Q., et al. 2018. Numerical

analysis of geocell-reinforced retaining wall failure

modes. Geotextiles and Geomembranes, 46(03): 284-

296.

Ehsan, S. H., Ahoo, A. 2018. Numerical simulation of two-

tier geosynthetic reinforced soil walls using two phase

approach. Computers and Geotechnics, 100:15-29.

Mohammad, R. S., Jie, H., Sazzad, B. S., et al. 2018. Study

of the behavior of mechanically stabilized earth (MSE)

walls subjected to differential settlements. Geotextiles

and Geomembranes, 46(01): 77-90.

Xiao, C. Z., Li, G. Q., Gao, S., et al. 2021. Dynamic

response of tiered geogrid-reinforced soil retaining

walls under traffic loading. Chinese Journal of

Geotechnical Engineering, 43(10): 1789-1797+1961.

Wang, J. Q., Zhong, W. T., Huang, S. B., et al. 2023.

Experimental study on static and dynamic

performances of modular reinforced earth retaining

wall. Rock and Soil Mechanics, 44(05): 1435-1444.

Ren, F. F., Xu, H., Huang, Q. Q. 2021. Study on

deformation and failure mechanisms of reinforced soil

retaining walls subjected to horizontal static/dynamic

loading. Chinese Journal of Rock Mechanics and

Engineering, 40(06): 1248-1257.

Xu, P., Zhong, Y., Ma, H. D., et al. 2023. Upper bound

analysis of bearing capacity of reinforced soil retaining

walls under strip footing load. Journal of Railway

Engineering Society, 40(03): 14-19.

Yang, G. Q., Niu, X. D., Zhou, S. G., et al. 2021.

Experimental study on structural behavior of reinforced

retaining wall with composite full-height rigid facing.

Rock and Soil Mechanics, 42(07): 1794-1802.

Du, Y. X., Liu, H., Zhou, F. 2018. Mechanical properties of

hybrid reinforced soil retaining wall. Journal of Central

South University (Science and Technology), 49(04):

940-948.

National Railway Administration Code for Design of High

Speed Railway: TB 10621-2014. Beijing: China

Railway Publishing House, 2014.

Yang, Y. T. 2015. The research on engineering properties

of QingRong intercity railway reinforced earth

retaining wall. ShiJiaZhuang TieDao University.

College of Civil Engineering, pp. 31-52.

Zhai, W. M. 2007. Vehicle-Track Coupling Dynamics

. 3rd

ed. Science Press, Beijing, pp. 390-400.

National Railway Administration. Code for design on

retaining structures of railway subgrade: TB 10025-

2019. China Railway Publishing House, Beijing. 2019.

Analysis of Soil Pressure Distribution and Fracture Surface Inside Mechanically Stabilized Earth (MSE) Walls of High-Speed Railways

181

Li, L., Zheng, J. J., Cao, W. Z., et al. 2020. Numerical

analysis of widening subgrade using pile-supported

reinforced-earth wall considering rhelogical

characteristics of subsoil. Journal of Civil and

Environmental Engineering, 42(02): 65-72.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

182