Structure Design of Jointless Cement Concrete Pavement

Zhihua Niu

and Xiaoyu Liu

2,* b

PowerChina Northwest Engineering Corporation Limited, No.18 Zhangba Road, Yanta District, Xi’an 710065, China

School of Civil Engineering, Xi’an University of Architecture and Technology, No. 13 Yanta Road, Beilin District,

Xi’an 710055, China

Keywords: Jointless Cement Concrete Pavement, Structure Design, ECC, Finite Element Model, Stress Analysis.

Abstract: Joints in cement concrete pavements frequently contribute to decreased ride quality, accelerated pavement

deterioration, and complex maintenance procedures. To mitigate these issues, this study proposes the use of

engineered cementitious composites (ECC) as connectors at pavement joints, creating a jointless cement

concrete pavement (JCCP) system. A finite element model was developed to evaluate the structural

performance of JCCP, taking into account variables such as vehicle loading, width and thickness of ECC

connector dimensions. The mechanical behavior of the JCCP under combined loading and temperature-

induced stresses was analyzed, and the critical load position was identified. The results reveal that the most

critical load position occurs directly above the induced crack in the pavement. The integration of ECC

connecting elements reduced the maximum tensile stress at the base of the pavement by nearly 50%. Based

on these findings, it is recommended to utilize ECC connectors with a width of 30 cm, and a thickness equal

to 50% of the pavement slab’s thickness.

1 INTRODUCTION

Compared to asphalt pavements, cement concrete

pavements have several advantages, including lower

construction costs, higher stiffness, longer service

life, and better stability (Plati 2019). However, the

application of cement concrete pavements in high-

class highways has been declining due to the negative

impacts of joints, such as poor ride quality, increased

susceptibility to pavement distresses, and difficult

maintenance. To address these limitations,

optimizing the joint design of cement concrete

pavements, reducing the number of joints, and even

achieving jointless constructions can significantly

improve pavement performance and promote the

wider adoption of cement concrete pavements in

high-class highways.

To mitigate cracking induced by temperature and

shrinkage stresses in concrete pavements, equally

spaced transverse and longitudinal joints are typically

constructed to accommodate these stresses (Das et al.,

2020). Joints are critical components of concrete

https://orcid.org/0009-0000-9338-1508

https://orcid.org/0009-0004-5745-0341

pavements but are also the weakest points, prone to

failures such as slab pumping, faulting, and spalling.

Existing research has demonstrated that the majority

of distress in concrete pavements is concentrated

around joint edges, particularly at the corners where

transverse and longitudinal joints intersect. Existing

measures to mitigate the adverse effects of joints

primarily involve regular cleaning and maintenance

of the pavement surface and joints, especially during

the early stages of service life. However, these

measures can only delay the onset of joint-related

distress and do not fundamentally eliminate the

negative impacts of joints.

Engineered Cementitious Composites (ECC)

exhibit exceptional ductility and toughness, with

ultimate tensile strains reaching 3-8%, which is 300-

800 times that of ordinary concrete (Li 1993). This

superior deformability makes ECC an excellent

candidate for accommodating deformations in

concrete pavements induced by temperature

variations (Arce et al., 2021). Moreover, ECC

possesses outstanding crack control capabilities,

dispersing single cracks in ordinary concrete into

102

Niu, Z., Liu and X.

Structure Design of Jointless Cement Concrete Pavement.

DOI: 10.5220/0013574200004671

In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 102-108

ISBN: 978-989-758-764-1; ISSN: 3051-701X

multiple microcracks with widths less than 100 μm,

and exhibiting self-healing properties (Shi et al.,

2017). The ultra-high toughness, high tensile strain

capacity, and superior crack resistance of ECC enable

it to absorb the deformations caused by thermal

stresses in concrete pavements (Singh et al., 2019) By

undergoing tensile and compressive deformations,

ECC can accommodate structural deformations

resulting from temperature changes. Additionally,

the exceptional ductility and multiple cracking

characteristics of ECC effectively inhibit and delay

the initiation and propagation of cracks in concrete

pavements, thereby prolonging the service life of the

entire pavement structure (Ismail et al., 2018). Zhang

et al. (Zhang et al., 2017; Zhang et al., 2013) explored

the performance of jointless concrete pavements and

found that ECC could continue to transmit forces

even after cracking. Although a limited number of

studies have been conducted on the application of

ECC in jointless concrete pavements in China (Cao

2021), specific structural design parameters for ECC

have not been clearly established, and corresponding

design methods are lacking. This paper develops a

finite element model of a jointless concrete pavement

structure, considering the effects of loading and

temperature stresses, to investigate and analyze the

mechanical response of the pavement structure under

various ECC connecting segment widths and

thicknesses. The objective is to determine the optimal

design parameters for ECC connecting segments in

jointless concrete pavements and to optimize the

design of jointless concrete pavement structures.

2 PAVEMENT STRUCTURE AND

MATERIALS

This paper establishes two types of pavement

structures: jointed plain concrete pavement (JPCP)

and jointless cement concrete pavement (JCCP).

Appropriate pavement materials were selected, and

ECC were prepared for use in the corresponding

pavement structures.

2.1 JPCP

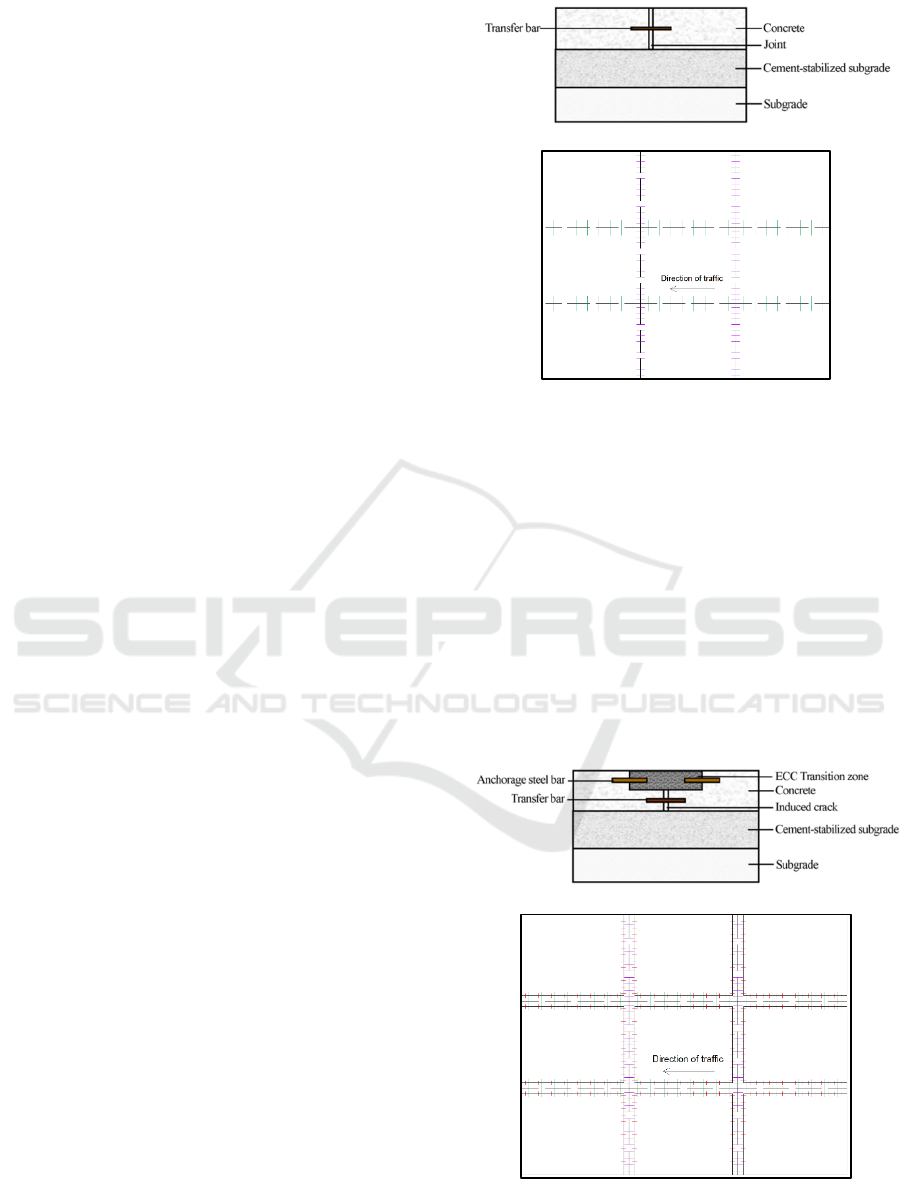
As shown in Figure 1(a), the JPCP structure consists

of a subgrade, a base course, and a surface course. As

illustrated in Figure 1(b), the surface course is

composed of nine 5 m×4 m×0.28 m concrete slabs

joined together with a 6 mm joint spacing. The base

course consists of a 0.36 m thick cement-stabilized

base layer.

(a) Pavement structure diagram

(b) Plan view of pavement structure

Figure 1: JPCP structure.

2.2 JCCP

As shown in Figure 2 (a), the JCCP structure is

developed based on the JPCP structure by replacing

the traditional joints with ECC transition zones. An

induced crack is set directly below the ECC transition

zone, with the transfer bar located at the middle of the

induced crack and the anchorage steel bars located at

the middle of the interface between the ECC

transition zone and the concrete slab. Figure 2 (b) is

a plan view of the JCCP structure, where both

transverse and longitudinal joints are replaced by

ECC transition zones.

(a) Pavement structure diagram

(b) Plan view of pavement structure

Figure 2: JCCP structure.

Structure Design of Jointless Cement Concrete Pavement

103

2.3 Pavement Materials

C50 concrete was selected as the cement concrete

surface layer material for both pavement structures,

while ECC material was prepared for the ECC

transition zone of the JCCP structure. The raw

materials for ECC included cement, fly ash, silica

sand, water reducer, and polyethylene (PE) fiber.

Four-point bending tests and elastic modulus tests

were conducted to determine the flexural strength of

C50 and ECC, which were found to be 5.1MPa and

20.0MPa, respectively. The elastic modulus of C50

and ECC were 36100MPa and 29800MPa,

respectively, and the subgrade reaction modulus was

60MN/m³. The pavement materials parameters are

shown in Table 1.

Table 1: Pavement material parameters.

Materi

als

Flex

ural

stren

gth

（

MPa

）

Elasti

modu

lus（

MPa

）

Poiss

on's

ratio

Dens

ity（

kg/m

³）

Thick

ness

（m

）

Concre

5.1

3610

0.15 2800 0.28

ECC

Transit

ion

zone

20.0

2980

0.15 2000 0.14

Cemen

stabiliz

ase

/ 1800 0.25 2200 0.36

Transf

er and

Tie bar

Ancho

rage

steel

2000

0.3 7850 /

Subgra

Reaction modulus: 60（MN/m³）

3 FINITE ELEMENT MODEL

ESTABLISHMENT AND

VERIFICATION

3.1 Establishment and Mechanical

Responses Analysis of Two

Pavement Models

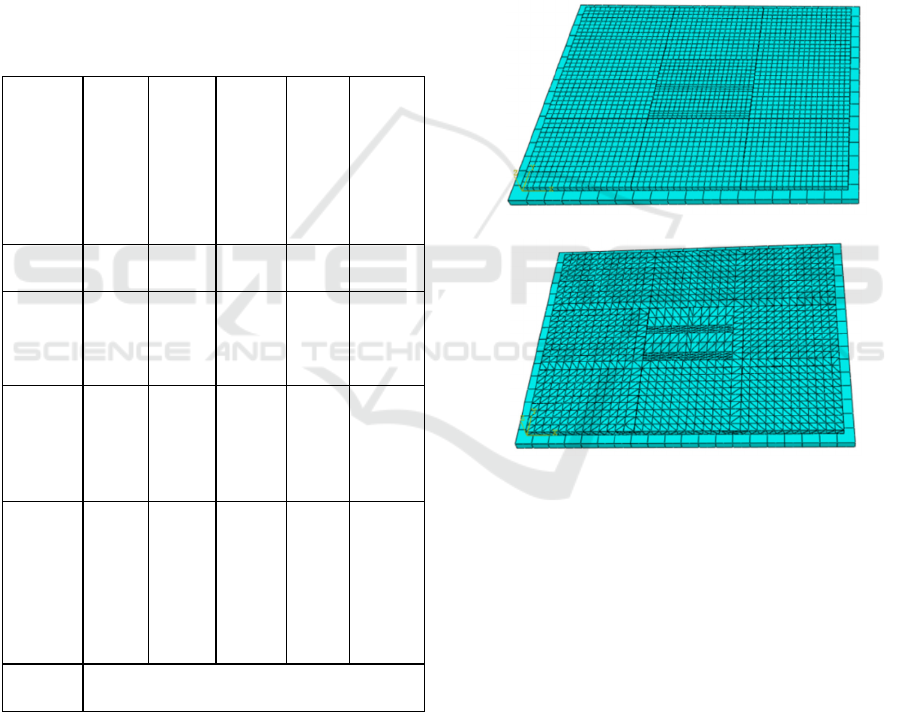
In this paper, two pavement structure models were

established using ABAQUS software to simulate and

analyze the mechanical response of the pavement

under load and temperature. As shown in Figures 3

(a) and (b), nine concrete slabs were set up in the

ABAQUS finite element model.

(a) Model of JPCP

(b) Model of JCCP

Figure 3: Finite element model of the pavement structure.

This study used a typical winter day in Xi’an with

a significant temperature gradient as a reference to

establish temperature field conditions for the two

pavement models (Wu 1992). The temperature field

was defined based on the temperature distribution at

various depths at the time of the lowest daily

temperature. Figure 4 illustrates the temperature

distribution at different depths at the moment of the

lowest daily temperature.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

104

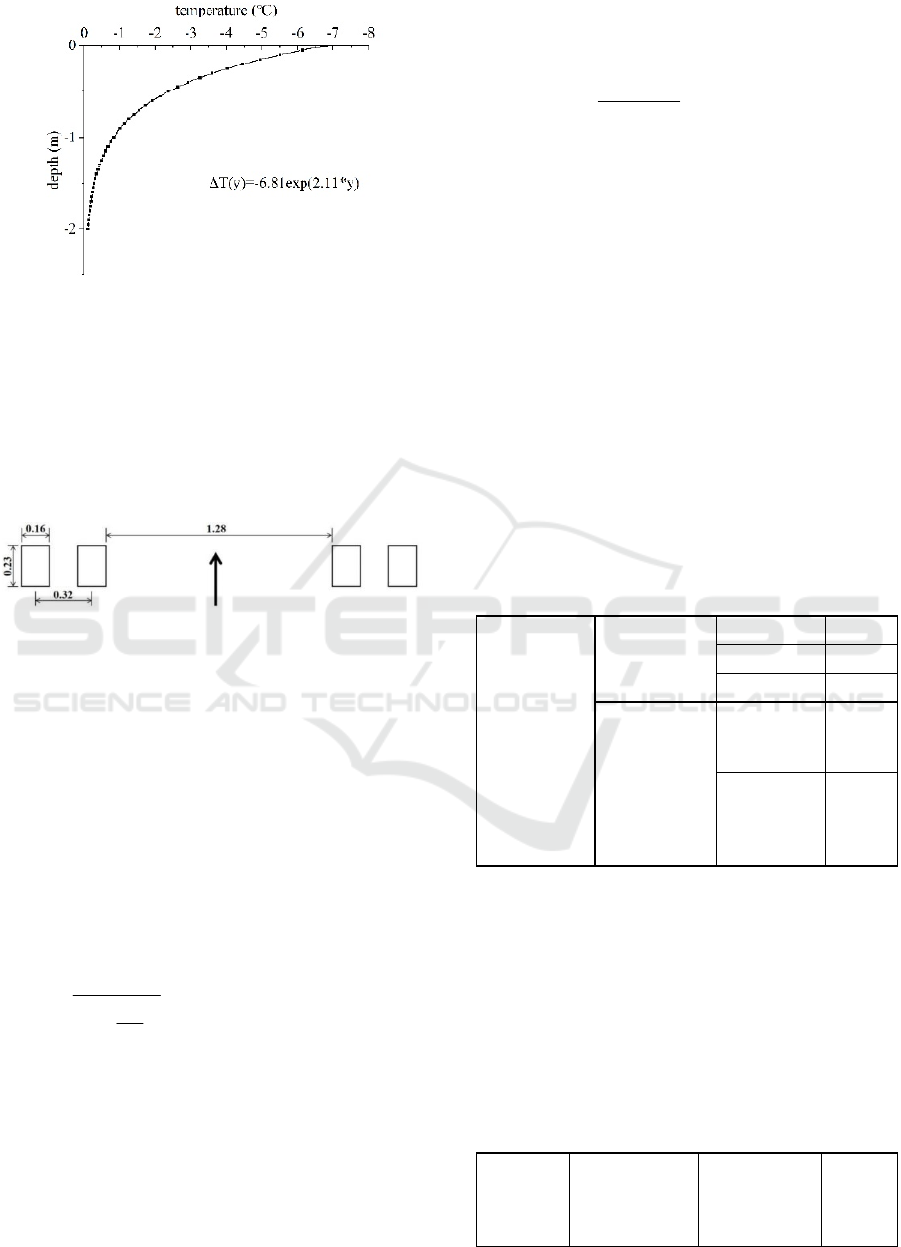
Figure 4: Minimum temperature at various depths in Xi’an.

In this study, a single-axle dual-wheel assembly

load was applied, with axle loads of 100kN, 150kN,

and 180kN, respectively. These axle loads were

converted into rectangular uniformly distributed

loads as shown in Figure 5. There were two wheels

on each side, with a center-to-center spacing of

0.32m. The contact area of the wheel load was

simplified as 0.23m × 0.16m.

Figure 5: Distribution of vehicle load on the pavement

(unit: m).

3.2 Stress Responses in JPCP

Based on the pavement structure and material

parameters in Section 2, the load stress and

temperature stress of ordinary Portland cement

concrete pavement are calculated. First, the stress in

the pavement slab under different axle loads was

calculated. Since the lower layer is made of cement-

stabilized gravel, there is no need to calculate its load

stress. Only the load stress of the upper cement slab

under the design load is calculated, which is obtained

from Equation 1:

0.65 2 0.94

pgc

1.45 10

rhP

−

σ=

(1)

where

σ is the stress due to load,

is the flexural

rigidity of the lower plate,

is the flexural rigidity

of the upper plate,

is the total relative stiffness

radius of the two-layer plate,

is the flexural

thickness of the upper plate, and

is the design

load.

The maximum temperature stress in the concrete

pavement slab under the maximum temperature

gradient is calculated as shown in Equation 2:

cccg

t,max L

EhT

σ=

(2)

where

is the coefficient of linear thermal

expansion of concrete,

is the modulus of

elasticity of the upper plate,

T is the maximum

temperature gradient, and

is the temperature

stress coefficient considering both temperature

warping stress and internal stress.

Equation 3 gives the calculated temperature

fatigue stress at the critical load position of the

surface layer.

tr t t,max

kσ= σ

(3)

where

is defined as the temperature fatigue stress

coefficient.

The theoretical calculation results of load stress

and temperature stress for JPCP are presented in

Table 2.

Table 2: Theoretical calculation results of JPCP stress

response (Unit: MPa).

Theoretical

Calculation

Results of

JPCP Stress

Response

load stress

100kN 1.501

150kN 2.198

180kN 2.609

temperature

stress

thermal

fatigue

stress

0.306

maximum

thermal

warping

stress

1.101

3.3 Finite Element Model Verification

A comparison between the finite element simulation

results and theoretical calculation results of JPCP

under load stress is presented in Table 3. The

maximum error between the two is 6.48%. Therefore,

the finite element model established in this paper is

reasonable and feasible.

Table 3: Comparison of finite element simulation and

theoretical calculation results for JPCP.

Axle

load

Theoretical

calculated

value (MPa)

Finite

element

simulation

value (MPa)

Error

(%)

Structure Design of Jointless Cement Concrete Pavement

105

100kN 1.501 1.490 0.73

150kN 2.198 2.122 3.46

180kN 2.609 2.440 6.48

4 INFLUENCE OF STRUCTURAL

DESIGN PARAMETERS OF

ECC JOINTS ON

MECHANICAL RESPONSE

4.1 Determination of Critical Load

Position

The critical load position for JPCP is at the mid-span

of the longitudinal joint, according to the design

code. However, as a novel pavement structure, the

critical load position of JCCP needs to be determined.

In this study, a JCCP structure with an ECC joint

width of 50 cm and thickness of 14 cm is taken as an

example to analyze the stress response of JCCP under

loads applied at five different positions. The five load

positions are as follows: (a) load at the mid-span of

the long side of the concrete slab, as shown in Figure

6(a); (b) load at the corner of the concrete slab, as

shown in Figure 6(b); (c) load directly above the

induced crack, as shown in Figure 6(c); (d) load at the

mid-span of the ECC joint, as shown in Figure 6(d);

(e) load on both sides directly above the induced

crack, as shown in Figure 6(e).

(a) At mid-span of the

lon

side

(b) At the corner

induced

oin

(d) At the mid-span of

the ECC

oin

(e) Both sides directl

above the induced crac

Figure 6: Different load positions.

The influence of different load positions on the

maximum tensile stress in each structural layer is

shown in Table 4 based on finite element simulation

results.

Table 4: Maximum tensile stress values in different load

positions. (unit: MPa).

Load

positions

Cement

concret

e slab

Base

course

join

bar

(a) At the

mid-span of

the long side

of the

concrete

slab

0.757 0.057

0.45

8.0

(b) At the

corner of the

concrete

slab

0.764 0.060

0.46

8.6

directly

above the

induced

crac

0.767 0.063

0.59

14.

811

(d) Load at

the mid-

span of the

ECC

oin

0.725 0.056

0.51

18.

210

(e) Load on

both sides

directly

above the

induced

crac

0.725 0.045

0.21

7.1

The maximum tensile stress at the bottom of the

JCCP surface layer is only about 50% of that of the

JPCP. Tensile stresses at the bottom of each layer

reach their maximum when the load is applied

directly above the center of the induced crack. The

maximum tensile stress at the bottom of the surface

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

106

layer under this condition is 0.767MPa. Conversely,

the minimum tensile stresses in each layer occur

when the load is applied on both sides directly above

the induced crack. Therefore, the critical load

position of the JCCP is determined to be directly

above the center of the induced crack.

4.2 Determination of Width of ECC

Joint

To investigate the influence of ECC joint width on

the stress response of JCCP, the ECC joint widths

were varied as 5cm, 10cm, 15cm, 20cm, 30cm, 40cm,

50cm, and 60cm. The upper width of the ordinary

concrete section varied accordingly, while the lower

part remained constant at 5m×4m. The thickness of

the ECC joint was still half of the surface slab. Figure

7 shows the variation of maximum tensile stress at

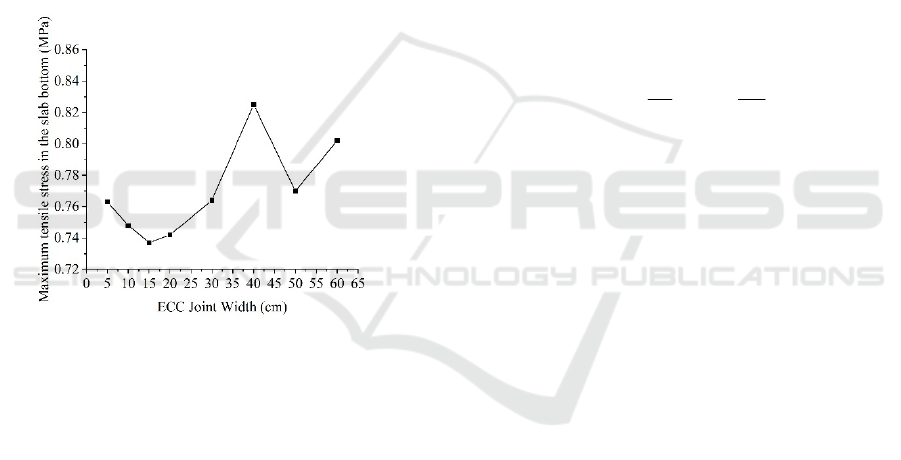
the bottom of the slab for different ECC joint widths.

Figure 7: Influence of ECC joint width on maximum tensile

stress at the slab bottom.

As shown in Figure 7, the maximum tensile stress

at the bottom of the slab initially decreases and then

increases with the increase of ECC joint width. The

minimum value of 0.737MPa is obtained when the

width is 15cm. When the ECC joint width is 40cm,

the maximum tensile stress at the bottom of the slab

increases abnormally, which is because the first

wheel on the left side of the single-axle dual-wheel

load in the driving direction acts entirely on the ECC

joint at this time, but its stress is 0.825MPa, which is

still less than that of JPCP.

In addition, concrete slabs are subjected to

temperature and shrinkage deformations. To prevent

cracking, joints are usually required in JPCP. For

JCCP, ECC has excellent ductility and deformability.

It is required that the ECC joint at the joint position

can absorb the tensile strain caused by temperature

and shrinkage deformation of the slab. Therefore,

when determining the width of the ECC joint, it is

necessary to ensure that the ultimate tensile strain of

ECC is not less than the required value of the overall

tensile strain of the slab. The required value of the

overall tensile strain of the slab can be calculated

theoretically and is related to temperature and

concrete shrinkage deformation, as shown in

Equation 4.

RT sh

Tε=αΔ+ε

(4)

where

is the required tensile strain of the entire

pavement slab,

is the thermal expansion

coefficient of concrete, typically taken as 0.001%/°C,

TΔ

is the annual temperature difference (about 40°C

in Xi'an), and

is the concrete shrinkage strain,

typically 0.06%. The calculated value of

0.10%.

The overall strain capacity of the pavement slab

in the longitudinal direction under uniaxial tension is

given by Equation 5.

  

ε=ε +ε

  

  

ⅠⅡ

(5)

where

Ⅰ

is the ultimate tensile strain of ECC,

Ⅱ

the strain of concrete under the corresponding axial

tensile load,

is the length of the pavement slab,

and

LandL

ⅠⅡ

are the lengths of the ECC and

concrete sections, respectively.

Both the ultimate tensile strain and width of the

ECC joint can enhance the overall deformation

capacity of the slab. For a 5m long slab, a

conservative value of 1.5% is adopted for the ultimate

tensile strain of the ECC joint, while the strain of

concrete under corresponding axial tensile load is

obtained from experiments and is taken as 0.01% in

this case. Substituting the required strain value

obtained from the above equation into the overall

deformation capacity, we finally obtain:

L 268.46mm L 4731.54mm==

ⅠⅡ

、

.Considering

the calculation results and a certain safety factor, as

well as construction convenience, the width of the

ECC joint for a 5.0m long slab is determined to be

300mm.

4.3 Determination of Thickness of

ECC Joint

To investigate the influence of ECC joint thickness

on the stress response of JCCP, the ECC joint

thickness was varied as 25%, 40%, 50%, 60%, and

75% of the pavement slab thickness. Figure 8

illustrates the variation of maximum tensile stress at

Structure Design of Jointless Cement Concrete Pavement

107

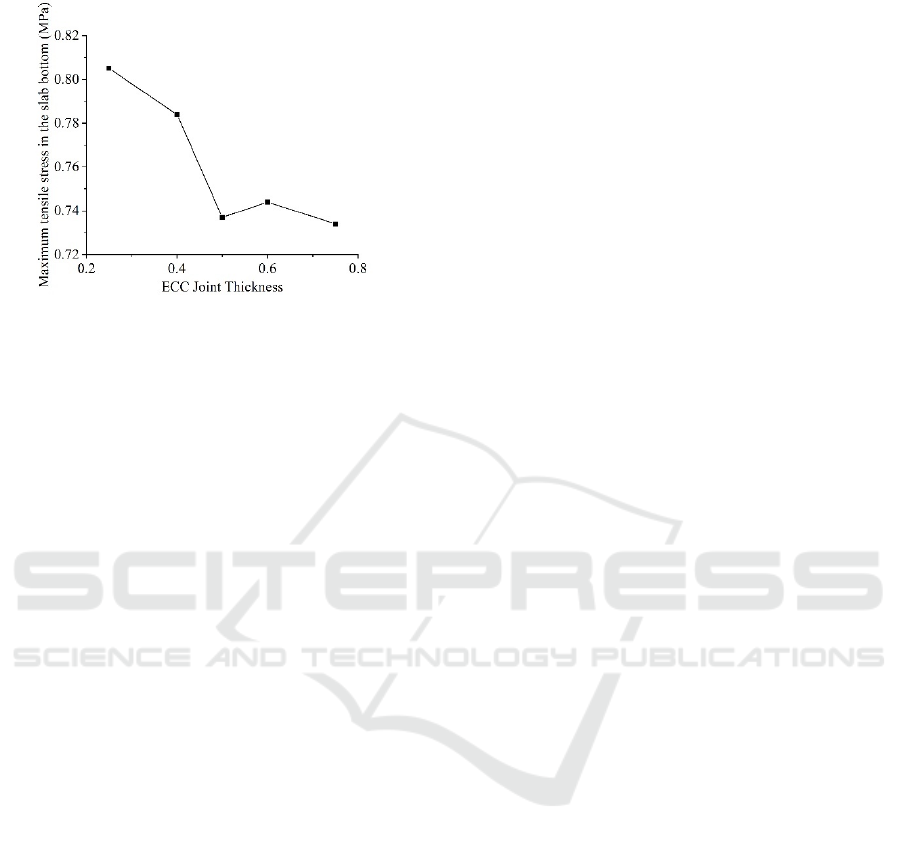
the bottom of the slab for different ECC joint

thicknesses.

Figure 8: Influence of ECC joint thickness on maximum

tensile stress at the slab bottom.

As shown in the Figure 8, the maximum tensile

stress at the bottom of the slab decreases with the

increase in the thickness ratio of the ECC joint. After

the thickness ratio reaches 50%, the change in the

maximum tensile stress at the bottom of the slab

becomes insignificant. The selection of ECC joint

thickness should also consider the diameter of the

anchor bars, force transfer bars, and tension bars, as

well as the concrete cover thickness. For the JCCP

structure proposed in this paper, it is recommended to

select an ECC joint thickness ratio of 50%.

5 CONCLUSIONS

In this study, a jointless concrete pavement with an

engineered cementitious composite (JCCP) was

designed, and a finite element model of the JCCP

structure was established. Considering the effects of

load stress and temperature stress, the influence of

vehicle load, ECC joint width, and thickness on the

mechanical response of JCCP was investigated and

analyzed, and the JCCP structure was optimized.

(1) Compared with JPCP, the maximum tensile

stress at the bottom of the JCCP surface layer is

only about 50% of that of JPCP, indicating that

JCCP can effectively reduce the stress in the

concrete slab.

(2) By comparing the stress responses of JCCP

under different load positions, it was

determined that the critical load position of

JCCP is the middle of the slab directly above the

induced crack.

(3) For the JCCP structure proposed in this paper, it

is recommended that the width of the ECC joint

be 30 cm, and the thickness be 50% of the

pavement slab thickness.

ACKNOWLEDGMENTS

This research was funded by Scientific Research

Program Funded by Education Department of

Shaanxi Provincial Government (Program

No.23JC046)

REFERENCES

Plati, C., 2019. Sustainability factors in pavement

materials, design, and preservation strategies: A

literature review. Construction and Building Materials

211, 539-555.

Das, A., Bhuyan, M.R., Khattak, M.J., Zhang, Q., 2020.

Mitigating reflective cracking in composite

pavements through the use of a ductile concrete

interlayer. Construction and Building Materials, 259,

120383.

Li, V.C., Stang, H., Krenchel, H., 1993. Micromechanics

of crack bridging in fibre-reinforced concrete.

Materials and Structures, 26, 486-494.

Arce, G.A., Noorvand, H., Hassan, M.M., Rupnow, T.,

Dhakal, N., 2021. Feasibility of low fiber content PVA-

ECC for jointless pavement application. Composites:

Part B, 50, 224-231.

Shi, T., Leung, C.K.Y., 2017. An effective discrete model

for strain hardening cementitious composites: Model

and concept. Computers and Structures, 185, 27-46.

Singh, M., Saini, B., Chalak, H.D., 2019. Performance and

composition analysis of engineered cementitious

composite (ECC) – A review. Journal of Building

Engineering, 26, 100851.

Ismail, M.K., Hassan, A.A.A., Lachemi, M., 2018. Effect

of Fiber Type on Impact and Abrasion Resistance of

Engineered Cementitious Composite. Aci Materials

Journal, 115(6), 957-968.

Zhang, J., Chen, Q., Wang, Z., Chen, C., Guo, Z., Fu, Y.,

2017. Design and construction of jointless concrete

pavement. Journal of Harbin Institute of Technology,

49(3), 68-73.

Zhang, J., Wang, Z., Ju, X., 2013. Application of ductile

fiber reinforced cementitious composite in jointless

concrete pavements. Composites: Part B, 50, 224-231.

Cao, W., 2021. Application of ECC Materials in Rigid-

flexible Composite Long-life Pavement. Journal of

Municipal Technology, 39(9), 180-183.

Wu, G., 1992. The Analysis of Pavement Temperature

Field of Multi-layer System. China Journal of Highway

and Transport, 5(5), 17-25.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

108