Estimation of Ultimate Soil Resistance for Laterally Loaded Piles

Using a Coupled Eulerian-Lagrangian Model

Shuanglong Li

1,* a

, Min Gong

, Limin Wei

, Yang Zhang

, Zengxiang Jiao

and

Qiaoxiong Chen

School of Hydraulic Engineering, Nanchang Institute of Technology, Nanchang 330099, China

School of Foreign Languages, Nanchang Institute of Technology, Nanchang 330099, China

School of Civil Engineering, Central South University, Changsha 410075, China

Teacher Development and Service Centre, Nanchang Institute of Technology, Nanchang 330099, China

Keywords: Laterally Loaded Piles, Soil Resistance, Eulerian-Lagrangian Model.

Abstract: In the numerical analysis of laterally loaded pile-soil interaction, the classical Lagrangian model under the

large soil deformation or rough pile-soil interface will cause convergence problems due to soil plastic

damage and great mesh distortion, which leads to a large discrepancy between the calculation results and the

actual situation. In this paper, a numerical model based on the coupled Eulerian-Lagrangian (CEL) method

was proposed to investigate the laterally loaded pile-soil interaction and the variation of ultimate soil

resistance (USR) acting on the pile side. The results show that the USR calculated by the CEL model was

consistent with the theoretical values and the Lagrangian model results in the literature, which indicates that

it is appropriate to study the laterally loaded pile-soil interaction behavior using the CEL model. In pile-soil

interaction problems involving large deformations, the CEL model describes well the soil flow behavior

around the pile and has significant advantages in the application.

https://orcid.org/0000-0001-9298-5561

1 INTRODUCTION

For laterally loaded piles (see Figure 1), the

deformation behavior of piles is mainly affected by

the distribution of ultimate soil resistance (USR) on

the pile side (Guo, 2006). Different assessment

results are inevitably obtained by using different

USR distributions. Therefore, accurate

determination of the USR on the pile side is essential

for the accurate design of the pile foundation.

To obtain the real USR, Abdrabbo et al. (2012)

and Kim et al. (2004) carried out a large number of

laboratory or field tests to investigate the

relationship between pile displacement and soil

resistance. Furthermore, Randolph and Houlsby

(1984) derived an upper-limit solution for the USR

of circular piles by considering the friction at the

pile-soil interface. Based on this theory, the USR

can be determined to be approximately 9.14c

D and

11.94c

D (where c

is the undrained shear strength

of the soil and D is the pile diameter) for smooth and

rough conditions at the pile-soil interface,

respectively.

Numerical simulation can be used to

quantitatively analyze the variation of the USR

under different conditions. Georgiadis et al. 0

adopted a finite element model to analyze the USR

in clay considering the effect of side-by-side piles.

Yang et al. (2002) developed an LPILE model to

study the deformation behavior of piles in

homogeneous sands and clays and obtained the pile

displacement-soil resistance curves. Zhao et al.

(2019) established an Abaqus 3D finite element

model to study the interaction characteristics

between laterally loaded piles and soil.

Li, S., Gong, M., Wei, L., Zhang, Y., Jiao, Z., Chen and Q.

Estimation of Ultimate Soil Resistance for Laterally Loaded Piles Using a Coupled Eulerian-Lagrangian Model.

DOI: 10.5220/0013573500004671

In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 66-70

ISBN: 978-989-758-764-1; ISSN: 3051-701X

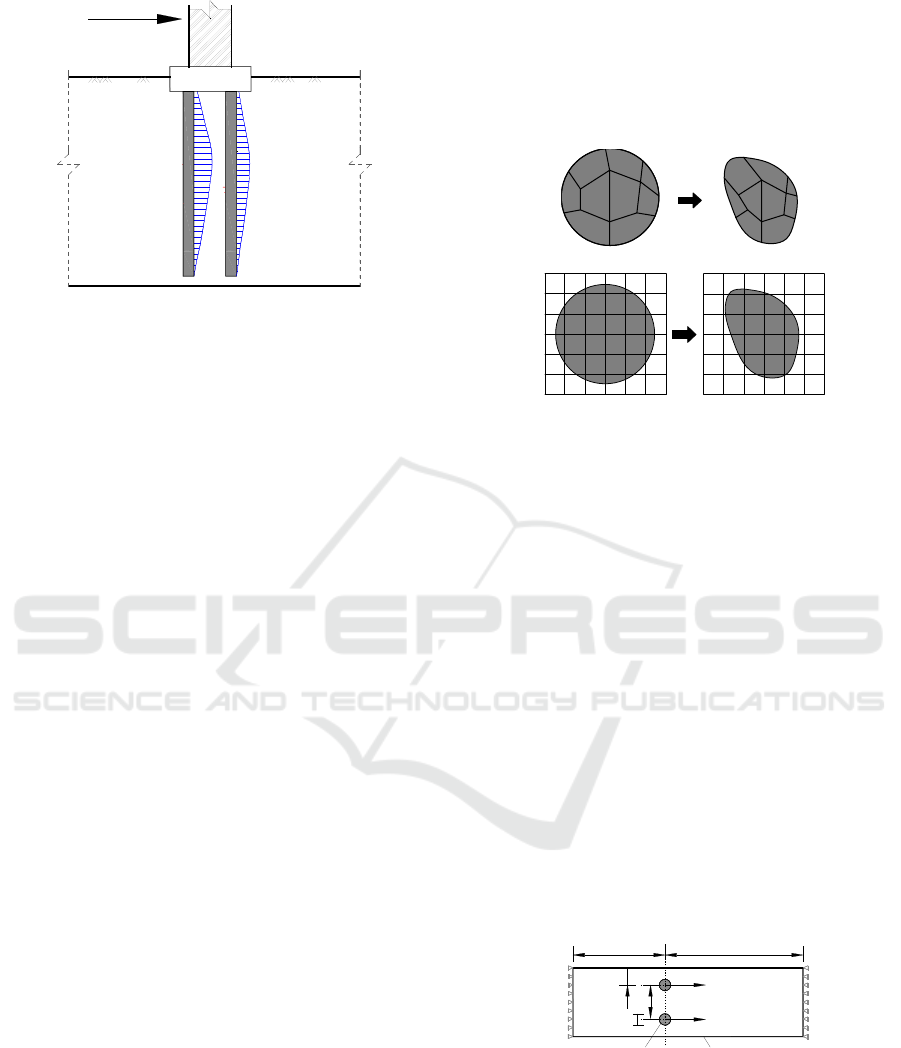
Figure 1: Schematic diagram of laterally loaded piles.

However, the numerical models adopted in the above

literature are quite different from the actual situation

when the soil deformation is large or the pile-soil

interface is rough. The reason is that the Lagrangian

model used in the above literature has convergence

problems due to the extreme plastic damage of the soil

and the great distortion of the mesh (Sheng et al., 2005).

Therefore, to further reveal the laterally loaded pile-soil

interaction mechanism and estimate the USR acting on

the pile side, this study aims to investigate this issue by

using a coupled Eulerian-Lagrangian (CEL) finite

element method considering large deformation

characteristics and to provide new ideas for the research

and engineering design of laterally loaded piles.

2 COUPLED EULERIAN-

LAGRANGIAN METHOD

CONSIDERING LARGE

DEFORMATIONS

The methods of describing material motion are classified

as Lagrangian or Eulerian, as shown in Figure 2. In the

Lagrangian method, the material is tightly connected to

the mesh and moves only with the deformation of the

mesh, whereas in the Eulerian method, the material can

flow freely in the Eulerian domain mesh but the mesh

always remains motionless. Since there is no need to

consider mesh quality issues (e.g. mesh distortion), the

Eulerian method has significant advantages for analyzing

problems involving large deformations and material

damage.

Combining Eulerian and Lagrangian methods to

form an advanced numerical analysis technique, i.e.,

the CEL method (Luke et al., 2021), which is

particularly suitable for the analysis of the

interaction between materials with large relative

stiffness and easy to yield by establishing the

Eulerian and Lagrangian bodies and allowing the

two to come into contact. For the pile-soil

interaction problem involved in this paper, the CEL

analysis will have a significant advantage due to the

large difference in pile-soil stiffness and the ease of

destruction of the soil.

Figure 2: Methods for describing the motion of materials.

3 ANALYSIS OF ULTIMATE SOIL

RESISTANCE FOR

LATERALLY LOADED PILES

3.1 Laterally Loaded Pile Model Based

on the CEL Method

Considering the side-by-side effect, the unit-length

laterally loaded pile-soil interaction model was

established, see Figure 3, where the pile diameter D

was 1.0 m, the s was the pile spacing, and the

boundary distance was s/2 from the pile axis.

Concerning the Lagrangian model adopted by Chen

and Martin (2002), the distance of the right

boundary from the pile axis was 12.0 m and the

distance of the left boundary from the pile axis was

8.0 m.

Figure 3: Numerical conceptual model for laterally loaded

piles.

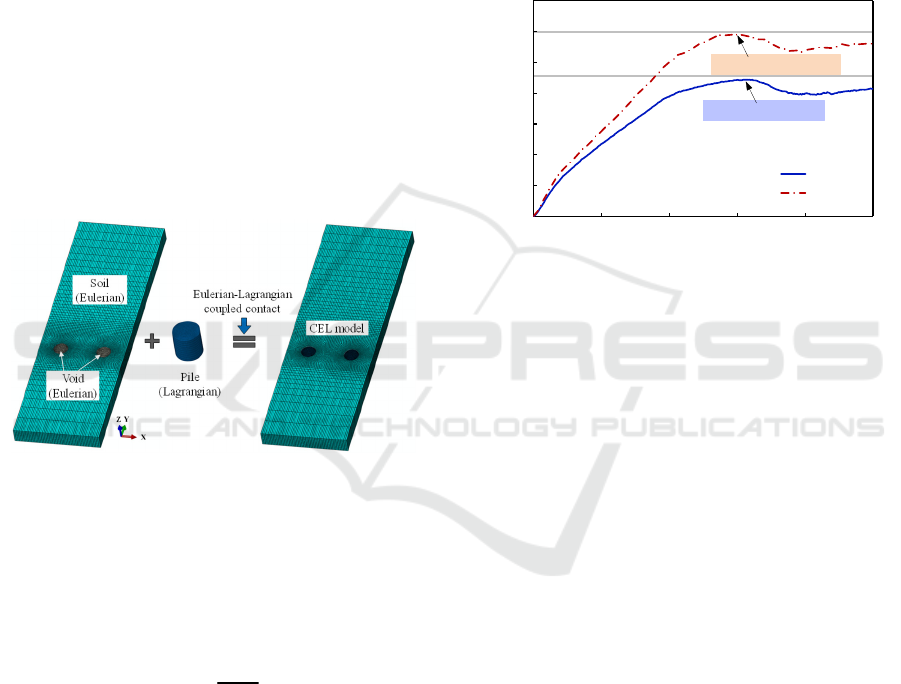
The established CEL finite element model is

shown in Figure 4. The soil region was modeled by

Eulerian material and the reserved pile region was

set as a void. The soil was described by the Mohr-

Pier

Cap

Soil

resistance

Pile

foundation

Lateral loads

Lagrangian method

Eulerian method

Soil

12.0 m8.0 m

s/2

Symmetric boundary

Pile

Pile velocity (v)

Fixed boundary

of velocity

Fixed boundary

of velocity

Estimation of Ultimate Soil Resistance for Laterally Loaded Piles Using a Coupled Eulerian-Lagrangian Model

Coulomb material model, with a density of 1642

kg/m

, and an elastic modulus of 6.0 MPa, and the

pile-soil interaction process was regarded as an

undrained process under rapid loading, then

Poisson's ratio was set to be the value of 0.495

(Georgiadis et al., 2013; Tho et al., 2014). The

friction angle was 0.1°, and the undrained shear

strength c

was 15.6 kPa. The unit-length pile was

modeled by Lagrangian material, which was

regarded as a linear material, with an elastic

modulus of 33.6 GPa, and a Poisson's ratio of 0.17.

The Eulerian-Lagrangian coupled contact was

established, and the friction factor at the pile-soil

interface was set to be f (the interface is represented

to be smooth when f=0, and the interface is

represented to be rough when f=1.0). The pile was

moved horizontally laterally at a speed of 0.001 m/s

for a calculation time of 100 s, and the variation in

pile reaction force (whose magnitude is equal to the

soil resistance p) was recorded through a reference

point.

Figure 4: The establishment process of the CEL model.

3.2 Variation in the USR

Figure 5 shows the development of soil resistance of

a monopile for friction factors of 0 and 1.0,

respectively. The soil resistance is normalized in the

figure in the following way

(1)

where N

is the soil resistance factor.

As can be seen from the figure, with the increase

of pile horizontal displacement, the soil resistance

gradually increases and tends to stabilize after

reaching the limit. The whole development process

can be divided into three stages: (i) the soil is in the

elastic stage, the pile displacement is from 0 to 6.0

mm, and the soil resistance increases linearly; (ii)

the soil is in the elastic-plastic stage, the pile

displacement is from 6 to 60.0 mm, the soil

resistance increases to the limiting value, and the

increase decreases gradually; (iii) the soil is in the

plastic stage, the pile displacement is larger than

60.0 mm, the soil resistance reaches the limiting

value and then tends to stabilize.

In addition, the USR was 8.87 c

D and 11.86 c

under f=0 and f=1.0, respectively, which were in

good agreement with the theoretical results of

Randolph and Houlsby (1984), with a difference of

3.0% and 0.7%, respectively, indicating that it is

appropriate to study the laterally loaded pile-soil

interaction behavior using the CEL model.

Figure 5: Comparison of CEL model calculated results

with theoretical results from the literature.

Figure 6 shows the equivalent plastic strain

distribution when the soil resistance reaches the limit

value. When f=0, the pile-soil interface is smooth,

the soil undergoes bypassing along the pile surface,

the soil equivalent plastic strain region is overall

narrow, the maximum equivalent plastic strain is

small, and the distribution area of the triangular

wedge elastic zone is small. When f=1.0, the soil

cannot produce relative sliding along the pile

surface, resulting in the soil providing a greater

resistance, and the triangular wedge elastic zone

distribution area is larger.

0 20406080100

Limiting value=8.87

Limiting value=11.86

Theoretical value=11.94

Pile displacement (mm)

f=0

f=1.0

Theoretical value=9.14

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

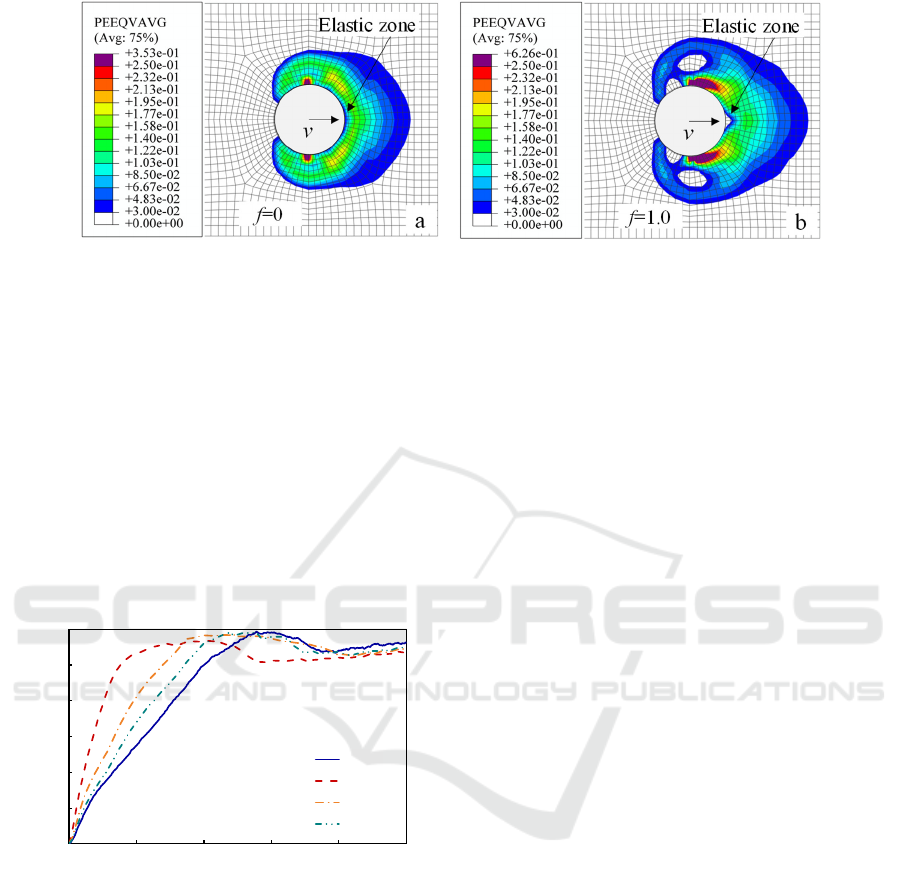
Figure 6: Equivalent plastic strain distribution of soil on the pile side.

Figure 7 shows the development of soil

resistance for different pile spacings at f=1.0. As the

pile spacing increases, the ‘stiffness’ of the soil

resistance development curve increases, and the

USR also increases, and gradually converges to the

USR under a single pile. Comparing these results

with those of Georgiadis et al. (2013), it can be seen

that the results of the CEL model are very close to

those of the literature, but the results of this paper

are overall small. The reason is that the CEL method

fully considers the large deformation effect of soil

flow around the pile, resulting in a relatively weaker

resistance given by the soil.

Figure 7: Development of soil resistance at different pile

spacings (f=1.0).

4 CONCLUSIONS

A CEL model was proposed to investigate the

mechanism of laterally loaded pile-soil interaction

and the variation of USR, and the following

conclusions were obtained:

(1) The USR calculated by the CEL model was

very close to the theoretical results and the

Lagrangian model results in the literature, which

indicated that it is reliable to analyze the laterally

loaded pile-soil interaction using the CEL method.

(2) The CEL method can overcome the

convergence problems caused by plastic yielding

and mesh twisting in the Lagrangian model and is

more applicable in pile-soil interaction problems

involving large deformation. Compared with the

Lagrangian model, the CEL model can well describe

the soil flow behavior around the pile.

ACKNOWLEDGMENTS

This paper reports research developed under

financial support provided by the Natural Science

Foundation of Jiangxi Province (Grant No.

20242BAB20230), the Science and Technology

Research Project of Jiangxi Education Department

(Grant No. GJJ2201509), and the National Natural

Science Foundation of China (Grant No. 51878671).

REFERENCES

Guo, W. D. 2006. On limiting force profile, slip depth and

response of lateral piles. Computers & Geotechnics,

33(1): 47-67.

Abdrabbo, F. M., Gaaver, K. E. 2012. Simplified analysis

of laterally loaded pile groups. Alexandria

Engineering Journal, 51(2): 121-127.

Tak Kim, B., Kim, N. K., Jin Lee, W., Su Kim, Y. 2004.

Experimental load-transfer curves of laterally loaded

piles in nak-dong river sand. Journal of Geotechnical

& Geoenvironmental Engineering, 130(4): 416-425.

Randolph, M. F., Houlsby, G. T. 1984. The limiting

pressure on a circular pile loaded laterally in cohesive

soil. Geotechnique, 34(4): 613-623.

Georgiadis, K., Sloan, S. W., Lyamin, A. V. 2013.

Ultimate lateral pressure of two side-by-side piles in

clay. Geotechnique, 63(13): 1170-1175.

0 20406080100

0.0

2.0

4.0

6.0

8.0

10.0

12.0

Pile displacement (mm)

Single

s/D=2

s/D=4

s/D=6

Estimation of Ultimate Soil Resistance for Laterally Loaded Piles Using a Coupled Eulerian-Lagrangian Model

Yang, Z., Jeremic, B. 2002. Numerical analysis of pile

behavior under lateral loads in layered elastic-plastic

soils. International Journal for Numerical and

Analytical Methods in Geomechanics, 26: 1385-1406.

Zhao, M., Peng, W., Yang, C., Xiao, Y. 2019. Analysis of

strain wedge for laterally loaded pile based on

ABAQUS. Journal of Railway Science and

Engineering, 16(09): 2199-2206.

Sheng, D., Eigenbrod, K. D., Wriggers, P. 2005. Finite

element analysis of pile installation using large-slip

frictional contact. Computers and Geotechnics, 32(1):

17-26.

Luke, T., Ashley, P., Ali, T. 2021. Coupled Eulerian-

Lagrangian simulation of a modified direct shear

apparatus for the measurement of residual shear

strengths. Journal of Rock Mechanics and

Geotechnical Engineering, 13(05): 1113-1123.

Chen, C. Y., Martin, G. R. 2002. Soil–structure interaction

for landslide stabilizing piles. Computers &

Geotechnics, 29(5): 363-386.

Tho, K. K., Chen, Z., Leung, C. F., Chow, Y. 2014.

Enhanced analysis of pile flexural behavior due to

installation of adjacent pile. Canadian Geotechnical

Journal, 51(6): 705-711.

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering