Prediction Using Kriging Surrogate Model Based on the

Formalization of Excavation Deformation Characteristics

Zhifeng Liu

, Jinpeng Chen, Chaojie Xia and Xinpeng Yan

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210024, China

Keywords: Hydraulic Tunnel, Formulaic Curve, Surrogate Model, Excavation Deformation Behavior, Rapid Prediction.

Abstract: The deformation characteristics of a tunnel during the advancement of the excavation face are crucial for

determining the excavation support scheme. Traditional simulation analysis methods often involve a

substantial workload and lengthy computation times. In this study, we propose a method to formulate the

tunnel excavation deformation characteristic curve. By combining Latin Hypercube Sampling techniques

with the Kriging surrogate model, we introduce a rapid prediction method for tunnel excavation deformation

characteristics based on the surrogate model. Case studies demonstrate that this method offers good

applicability and high prediction accuracy. Compared to traditional simulation analysis methods, this

approach is significantly more efficient.

https://orcid.org/0009-0004-6819-9914

1 INTRODUCTION

Hydraulic tunnels, as a critical component of

hydraulic infrastructure systems, exhibit deformation

characteristics during excavation that are of

paramount concern to engineers (Zhang et al., 2017).

These characteristics serve as a crucial basis for

determining the stability and safety of the

surrounding rock, as well as for designing support

measures and selecting the timing of such support

(Ren et al., 2021; Liu et al., 2023). Consequently, the

ability to rapidly predict the deformation

characteristics of the surrounding rock under various

excavation schemes is essential.

Su Kai et al. (2019) analyzed the deformation

patterns of the surrounding rock during the

advancement of a tunnel face through numerical

simulation. They introduced the concept of

displacement completion rate and applied it to

determine the timing of initial support installation.

However, numerical simulation methods are labor-

intensive and time-consuming. Zhou Shuoan (2014)

developed a surrogate model based on neural

networks to predict the deformation characteristics

of tunnels, using parameters such as rock mass

deformation, strength, and depth ratio as inputs.

However, this model is limited to predicting

deformation at a specific moment and cannot

forecast the progression of deformation over time.

To address these issues, this paper proposes a

rapid prediction method for the deformation

characteristics curve during tunnel excavation. First,

by thoroughly analyzing the spatial effects of tunnel

excavation and the trend of the tunnel deformation

characteristics curve, a parametric representation

method for the deformation characteristics curve of

the surrounding rock is proposed. Then, by

integrating Latin Hypercube Sampling with the

Kriging surrogate model, a rapid prediction of the

tunnel excavation deformation characteristics curve

is achieved. Case studies have demonstrated the

effectiveness of this method.

2 METHOD

2.1 Formulated Deformation

Characteristic Curve of Tunnel

Excavation

Tunnel excavation refers to the process of removing

geotechnical materials from the predetermined

location of the tunnel using a specified excavation

method. During the advancement of the excavation

Liu, Z., Chen, J., Xia, C., Yan and X.

Prediction Using Kriging Surrogate Model Based on the Formalization of Excavation Deformation Characteristics.

DOI: 10.5220/0013573300004671

In Proceedings of the 7th International Conference on Environmental Science and Civil Engineer ing (ICESCE 2024), pages 54-59

ISBN: 978-989-758-764-1; ISSN: 3051-701X

face, the rock mass structure surrounding the tunnel

continuously changes, leading to deformation within

the excavation disturbed zone. The magnitude and

distribution characteristics of the deformation in the

surrounding rock mass are not only related to the

excavation at the current location but are also

influenced by excavation activities within a certain

range both ahead and behind the face. Consequently,

rock mass deformation is gradually completed

during a specific stage and is subject to spatial

effects.

Since the deformation within the excavation

disturbed zone gradually decreases from the

excavation boundary to the deeper surrounding rock,

the tunnel excavation design primarily focuses on

the development and evolution characteristics of

rock mass deformation at key points on the

excavation boundary during construction. This is to

adequately evaluate the stability of surrounding rock

deformation and design the support scheme.

Therefore, in this study, the vertical displacement at

the tunnel crown of a typical section is denoted as

'u,' the distance between this section and the

excavation face is denoted as 'L,' and the curve of 'u'

varying with 'L' is termed the 'tunnel excavation

deformation characteristic curve.' The tunnel

excavation deformation characteristic curve is

rapidly predicted using a surrogate model.

Since the surrogate model cannot output a

continuous tunnel excavation deformation

characteristic curve, it is necessary to formulate the

tunnel excavation deformation characteristic curve.

This involves representing the curve with an

equation that contains a finite number of

undetermined coefficients. Based on the observed

variation characteristics of the tunnel excavation

deformation characteristic curve, a function like the

one shown in Equation (1) is selected to express the

relationship between u(mm) and L(m).

max

−

(1)

where u

max

represents the maximum deformation

during excavation, k denotes the rate of change of

the deformation rate in the tunnel excavation

deformation characteristic curve, a indicates the

proportional relationship between the deformation at

L=0 and u

max

In summary, due to the limited output data from

the Kriging model, predicting a continuous curve

presents a challenge. Formula 1 proposed in Part 2

can represent the deformation characteristic curve of

tunnel excavation, which implies that the prediction

of the tunnel excavation deformation characteristic

curve can be transformed into predicting the values

of the three undetermined coefficients. This avoids

the difficulty of directly predicting a continuous

curve using a surrogate model, representing one of

the innovations of this paper.

2.2 Kriging Surrogate Model

The Kriging model is an interpolation model that

assumes the response value at any point xxx in the

input space can be expressed as a linear weighted

sum of the known sample response values, as

follows:

()

()( )

yx xyx



(2)

where

()

represents the weighting coefficient

for the i-th sample's true response value, and

()

is the true response value corresponding to the i-th

known sample point x in the model's input space.

Together,

and

()

form the i-th sample's

input-output data pair. n is the number of known

sample points.

To determine the weighting coefficients, the

Kriging model treats the unknown function to be

fitted as the realization of a Gaussian stationary

stochastic process:

() ()

Yx Zx

(3)

where μ is an unknown constant representing the

mean of

()

, and

()

is a stationary stochastic

process with a mean of 0 and variance

. The

covariance of this process is given by:

() ( ) ( )

,,Cov Z x Z x R x x

′′

=



(4)

where

()

′

is the correlation function, used to

define the correlation between any two points x and

′

. A common choice is the Gaussian correlation

function (Han, 2016):

()

(

)

ii i

R x x exp x x





′

=− −









(5)

In this equation,

is a hyperparameter that

measures the influence of the i-th input variable

on the model and must be optimized using

maximum likelihood estimation (Kaymaz, 2005;

Dong et al., 2024).

To minimize the mean squared error (MSE) of

the predictions and ensure unbiasedness, the optimal

weighting coefficients must be determined. This is

done by minimizing the MSE:

Prediction Using Kriging Surrogate Model Based on the Formalization of Excavation Deformation Characteristics

[]

ˆˆ

() (())MSE y x Var y x=

(6)

while satisfying the unbiasedness condition:

() 1



(7)

Applying the Lagrange multiplier method, the

best linear unbiased prediction (BLUP) for

()

can be obtained (Wan et al., 2023):

()

yx rR Y F

μμ

−

=+ −

(8)

where

()

11TT

FR F FRY

−

−−

is the

correlation vector between the prediction point x and

the known sample points,

−

is the n×n correlation

matrix composed of the correlation function values

between all known sample points,

is the n-

dimensional vector of known sample true response

values, and F is an n×1 column vector of ones.

2.3 Excavation Deformation

Characteristics Curve Prediction

Method Based on the Kriging

Surrogate Model

Based on the formulation of the tunnel excavation

deformation characteristic curve, the Kriging

surrogate model is established to achieve rapid

prediction of the tunnel excavation deformation

characteristic curve. The inputs to this model are the

primary influencing factors of tunnel excavation

deformation characteristics, and the outputs are the

formulation coefficients of the curve (i.e., u

max

, k,

and a). This process primarily involves the selection

of influencing factors, generation of the sample set,

training of the surrogate model, and prediction.

In this study, the deformation modulus E,

Poisson's ratio μ, internal friction angle φ, cohesion

c, and depth H are selected as the influencing

factors, which serve as the inputs to the surrogate

model.

Given the advantage of Latin Hypercube

Sampling (LHS) in reflecting overall variability with

a smaller sample size (McKay et al., 2012), LHS is

employed to sample the surrogate model inputs. The

corresponding model outputs for each sampled point

are obtained through a combination of finite element

analysis and Equation (1).

A total sample set is then formed, which is

divided into a training sample set for training the

surrogate model and a testing sample set for

validating the model's prediction accuracy.

Based on these training and testing samples, the

Kriging surrogate model is constructed and its

prediction accuracy is verified.

For any given set of surrogate model input data

(i.e., values of deformation modulus E, Poisson's

ratio μ, internal friction angle φ, cohesion c, and

depth H), the u~L functional relationship curve

describing the tunnel excavation deformation

characteristics can be obtained using Equations (8)

and (1). Figure 1 illustrates the implementation

process of this method.

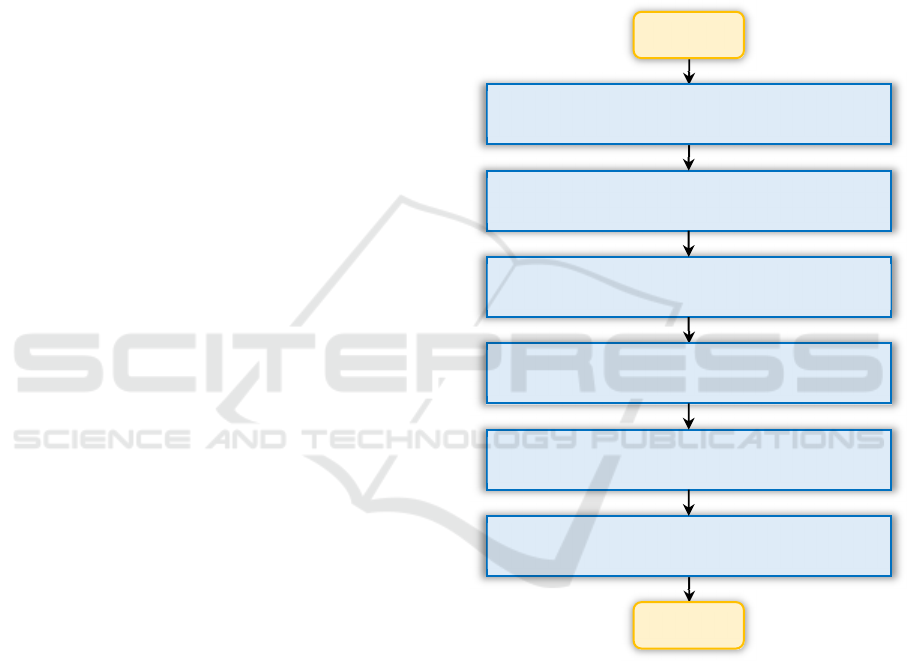
Figure 1: Prediction of Tunnel Excavation Deformation

Characteristics Implementation Procedure.

3 EXAMPLE

3.1 Project Overview

A certain water conveyance tunnel has a total length

of approximately 3.5 km, with a burial depth ranging

from 260 to 460 meters. The rock primarily consists

of dolomite and limestone. The tunnel has a circular

cross-section, with an excavation diameter D of 6.8

Conduct finite element analysis for each

sample

Perform LHS within the model input space

Obtain output for each sample based on

equation (1)

Determine the variables in the surrogate

model's input space

Train and test the Kriging surrogate

model

Develop predictions of the deformation

characteristics curve for tunnel

egin

end

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

meters and an advance rate of 2 meters per round.

The range of rock mass mechanical parameters is

provided in Table 1.

Table 1: Range of rock mass mechanical parameters.

ρ (kg

) φ (°) c (MPa) E (GPa)

2650 35~45 0.5~1 5~10 0.24~0.28

3.2 Training and Testing of Kriging

Figure 2 illustrates the finite element mesh in the

central portion of the model, extending

approximately five times the excavation advance

length. The model dimensions are

X×Y×Z=74.8m×204m×74.8m, with the tunnel

located at the center of the model. A uniformly

distributed vertical compressive stress is applied to

the top of the model, while normal displacement

constraints are applied to the bottom and sides.

After completing the finite element simulation

analysis for all training sample points, the surrogate

model output data, namely u

max

, k, and a, can be

obtained based on Equation (1) and the results of the

simulation analysis. On the basis of obtaining the

training sample set, the Kriging surrogate model for

predicting the deformation characteristics of tunnel

excavation can be trained according to the principles

described in Section 3. Table 2 compares the

surrogate model predicted values and the fitted

values of the undetermined coefficients for three test

sample points (VS1, VS2, VS3), showing that the

maximum relative error does not exceed 2%,

indicating that the constructed surrogate model has

good predictive accuracy.

Figure 2: Finite Element Mesh Diagram.

3.3 Analysis of Predicted Results

The Kriging surrogate model was used to predict the

excavation deformation characteristics of three

typical sections of the water conveyance tunnel

(Section 1, Section 2, Section 3). Table 3 lists the

burial depths and mechanical parameters of the

surrounding rock for the predicted sections.

Additionally, to validate the prediction accuracy,

finite element simulation analyses were conducted

for the three sections mentioned above in Figure 3.

Table 3: Typical hole depth and surrounding rock

mechanical parameters.

Section

number

φ (°)

(MPa)

(GPa)

μ H (m)

38.7 0.60 9.00 0.25 400

41.0 0.67 9.14 0.25 431

43.2 0.76 9.77 0.24 446

Table 2: Comparison between the predicted and fitted values of the undetermined coefficients for the test samples.

Test

Sample

max

(mm) a k

Fitted

value

Projected

value

Relative

erro

Fitted

value

Projected

value

relative

erro

Fitted

value

Projected

value

Relative

erro

12.61 12.69 0.63% 1.74 1.73 0.57% 0.59 0.60 1.69%

12.78 12.81 0.23% 1.85 1.84 0.54% 0.59 0.60 1.69%

12.94 12.95 0.07% 1.68 1.69 0.6% 0.63 0.64 1.58%

Typical Section

Prediction Using Kriging Surrogate Model Based on the Formalization of Excavation Deformation Characteristics

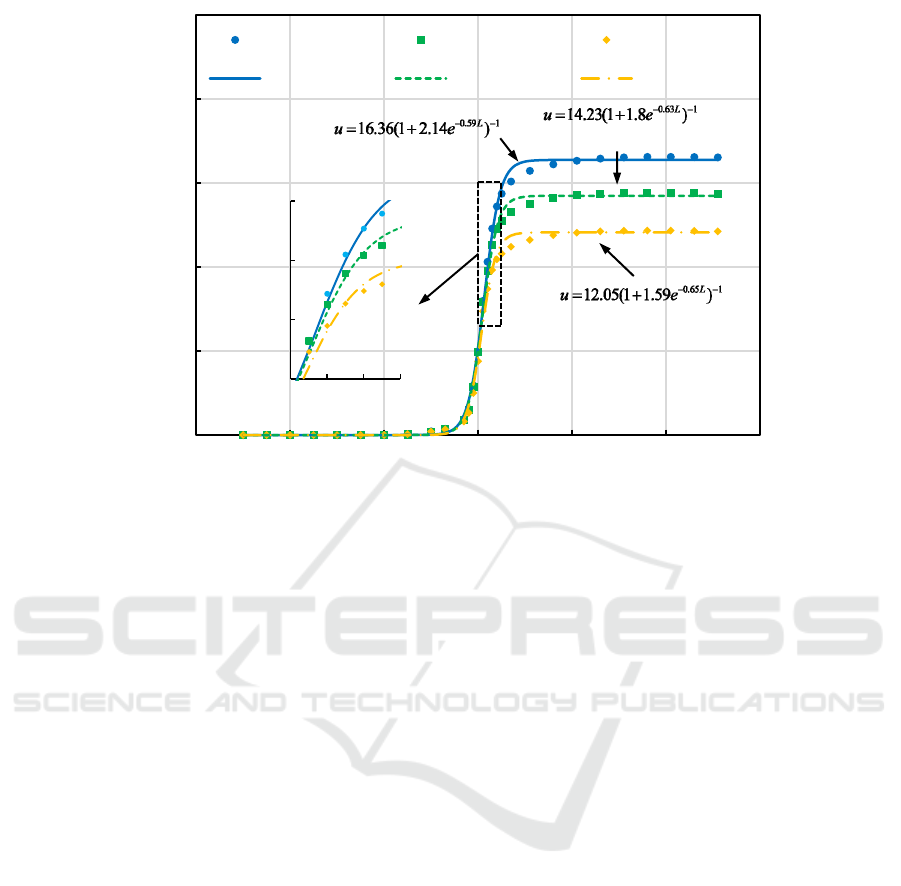
Figure 3: Comparison of prediction results and simulation analysis results.

The comparison of the surrogate model

prediction curves with the finite element simulation

results for Sections 1, 2, and 3 reveals the following:

(1) For sections with different burial depths and

varying mechanical parameters of the surrounding

rock, the surrogate model consistently provides

excavation deformation prediction curves that align

well with the simulation analysis results, indicating

reliable prediction accuracy and strong adaptability.

(2) The excavation deformation in different sections

primarily occurs during the excavation process of

the rock mass in front of and behind the observation

profile (-4m < L < 6m). Considering the need for

deformation control and the excavation cycle length

(2m), the initial support should be installed as soon

as possible after excavation, with the lag distance

behind the excavation face not exceeding 4m. (3)

The differences in excavation deformation

characteristics between sections are mainly reflected

in two aspects: the deformation rate and the

maximum deformation. From Section 1 to Section 3,

as the burial depth gradually increases, both the

deformation rate and the maximum deformation

decrease. This is primarily because when the

difference in burial depth is small, the mechanical

parameters of the rock are the main factors

influencing the deformation rate and deformation

magnitude.

4 CONCLUSION

To achieve rapid and accurate prediction of tunnel

excavation deformation characteristics, this study

proposes a rapid prediction method based on a

surrogate model, building on the formulation of the

excavation deformation characteristic curve. A case

study analysis was conducted to validate the method.

The main research conclusions are as follows:

(1) A formula containing three undetermined

coefficients was proposed. The trend of the curve

generated by this formula aligns with the growth

pattern of surrounding rock deformation during

tunnel excavation. This approach transforms the

prediction target from a continuous curve to

independent undetermined coefficients, thereby

reducing prediction difficulty.

(2) The constructed Kriging surrogate model can

predict the deformation characteristics of the tunnel

for given model inputs. This method is more

efficient than traditional simulation analysis

methods, significantly reducing computation time.

(3) The case study analysis verified the

prediction accuracy and applicability of this method.

The predicted excavation deformation characteristic

curve closely matches the results obtained from

simulation analysis.

-60 -40 -20 0 20 40 60

u/mm

L/m

1# - Simulation 2# - Simulation 3# - Simulation

1# - Prediction 2# - Prediction 3# - Prediction

0246

RMSE=0.24

RMSE=0.21

ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering

REFERENCES

Zhang, Y. J., Su, K., Zhou, L., et al. 2017. Study on the

longitudinal deformation evolution law of tunnels

based on the convergence-confinement method and

estimation of support timing. Rock and Soil

Mechanics, 38(S1): 471-478.

Ren, Q. W., Xu, L., Zhu, A. X., et al. 2021.

Comprehensive safety evaluation method of

surrounding rock during underground cavern

construction. Underground Space, 6(1): 46-61.

Liu, J., Chen, K. J., Sun, M., et al. 2023. Matrix

Compression Effect on Deformation Stability of High

External Water Pressure Tunnels. Journal of Water

Resources and Water Engineering, 24(5): 183-

189+197.

Su, K., Zhang, Y. J., Wu, H. G., et al. 2019. Study on the

evolution characteristics of the safety factor of

surrounding rock during tunnel excavation and the

selection method for support timing. Chinese Journal

of Rock Mechanics and Engineering, 38(S1): 2964-

2975.

Zhou, S. A. 2014. Determination of surrounding rock

displacement release coefficient considering spatial

effect. Chongqing: Chongqing University.

Han, Z. H. 2016. Research progress on Kriging model and

surrogate optimization algorithm. Acta Aeronautica et

Astronautica Sinica, 37(11): 3197-3225.

Kaymaz, I. 2005. Application of kriging method to

structural reliability problems. Structural Safety,

27(2): 133-151.

Dong, M., Cheng, Y., Wan, L. 2024. A novel adaptive

bayesian model averaging-based multiple kriging

method for structural reliability analysis. IEEE

Transactions on Reliability, 1-15.

Wan, Z. Y., Li, P., Yang, G., et al. 2023. Reliability

analysis of soil slopes based on surrogate models.

Journal of Wuhan University (Engineering Edition),

56(10): 1217-1223.

McKay, D. M., Beckman, J. R., Conover, J. W. 2012.

Comparison of three methods for selecting values of

input variables in the analysis of output from a

computer code. Technometrics, 21(2): 239-245.

Prediction Using Kriging Surrogate Model Based on the Formalization of Excavation Deformation Characteristics