
Analytic Study on High-Performance Concrete Column with
High-Strength Reinforcement Under Moment-Compress Loads
Xu Wang
a
School of Vocation Education, Xi'an Eurasia University, Dong Yi St. 8th sector, Xi’an 710065, Shaanxi Province, China
Keywords: Reinforced Concrete Column, High-Performance Concrete, High-Strength Reinforcement, Analytic Study.
Abstract: According to analytic calculation in RC column of high-performance concrete and high-strength
reinforcement, these rules on geometric deformation compatibility, physical constitutive relation and static
equilibrium were applied,the model of analytic calculation was confirmed and some equations on static
equilibrium were for reinforced high-performance concrete column with high-strength reinforcement. Some
calculation formulas on reinforcement and bearing capability were presented for moment-compressed
column by the KADAN formula and simplified calculation method.The research shows that good
agreements and small errors are observed by comparing the experimental data of bearing capability and the
result from proposed formulas. However some larger errors are observed from the formula of current code,
the error becomes larger with the strength promotion of reinforcement.
a
https://orcid.org/0009-0005-1436-9970
1 INTRODUCTION
Reinforced concrete compressed members are one of
the most common basic components in building
structures, the calculation on bearing capability and
reinforcement of columns became some important
parts of structural design. Some codes of structure
design took these calculation methods on bearing
capability and reinforcement for normal RC column
(GB50010, 2010; ACI318, 2010).
In recent years, high-performance concrete
(HPC) and high-strength reinforcemet (HSR) were
widely applied in RC building structures.Some
experiment studies and numerical analysis were
presented for high-performance concrete column
with high-strength steel bars. Monotonic eccentric
loading tests on eight reinforced concrete columns
with 630MPa grade steel bars were carried
out,630MPa reinforced concrete biased columns can
be calculated according to the bearing capacity
formula in specification GB 50010-2010. (Gao,
2023; Ma et al., 2024). Textile-reinforced concrete
(TRC) were replaced by high-strength high ductile
concrete (HSHDC) and some columns were tested
under eccentric loading, a calculation formula
considering strain-lag behavior was presented to
predict the maximum load of the column
strengthened with TR-HSHDC (Ding et al., 2024).
Axially-compressed behaviour of concrete columns
reinforced with novel high-strength steel-rebar
materials were studied by some tests,the
corresponding finite element (FE) model of the
axially-compressed RC-NHHSRs column was
established. (Shen et al., 2024). The influence of
eccentric axial loads on the lateral low-velocity
impact behaviors of RC columns was studied by the
numerical simulation approach (Jia et al., 2024).
However few analytic studies on bear capability
and reinforcement were taken for compressed
column of high-performance concrete and high-
strength reinforcement. The behaviors of
symmetrical reinforcement of concrete column with
HRB600 steel bars were analyzed under eccentric
compression,the basic formula under large or small
eccentric compression and the corresponding section
design calculation methods were given based on the
existing code for design of concrete structures
(GB50010—2010) (Zhang et al., 2021).
Wang and X.
Analytic Study on High-Performance Concrete Column with High-Strength Reinforcement Under Moment-Compress Loads.
DOI: 10.5220/0013559300004671
In Proceedings of the 7th International Conference on Environmental Science and Civil Engineering (ICESCE 2024), pages 5-9
ISBN: 978-989-758-764-1; ISSN: 3051-701X
Copyright © 2025 by Paper published under CC license (CC BY-NC-ND 4.0)
5

2 BASIC FORMULA ON
BEARING CAPABILITY OF RC
COLUMN
2.1 Overview on Calculation Method
Three kinds of internal force analysis were certified
for RC column and were shown as follows:
• Compressed column under axial load. For the
short-column under strength failure mode, the
capability bearing was equated to some limit
compressed forces from concrete and steel bar.
For the slender-column or moderate-column
under buckling mode or strength-buckling mode,
the bearing capability of short-column was
reduced by the stability coefficient of buckling.
• Compressed column under larger eccentric load.
It was named as moment member under tensile
failure mode, the bearing capability and
reinforcement were calculated by the method on
bearing capability of beam and axial compressed
column.
• Compressed column under small eccentric load.It
was named as compressed member under
compress failure mode, the bearing capability
was equated to compressed forces from concrete
and steel bar.
The bearing capability of RC column could be
calculated according to these codes of structure
design as GB50010-2010 or ACI318-19.
2.2 Method on Bearing Capability of
HPC-HSR Column
Number simulation analysis,analytical method and
testing method have been applied to analyze the
bearing capability of RC column with high-
performance concrete and high-strength steel bars.
These research methods were verified each other and
shown as follows:
• Finite element method of number simulation
analysis.The softwares of Aboqus or Anasys and
so on were applied to analyze the bearing
capability and reinforcement of HPC-HSR
column, however these analysis modes might be
modified for RC column with high-performance
concrete and high-strength steel bars.
• Formula analytic method of mathematical
method. According to the failure modes and
basic assumed conditions, some analytical
formulas of RC column were presented in
research literature,however some results from
theoretical formulas had more errors than some
test data.Many calculation formulas on bearing
capability of RC column were applied in some
structural design codes
• Testing method. Few testing on bearing
capability of HPC-HSR columns were conducted,
however some expensive fees, prolonged process
and many limit conditions were the shortcomings
in these testing methods.
2.3 Formulas for Bearing Capability of
HPC-HSR Column
2.3.1 Static Equations from Analysis Mode
According to some tests and analysis mode bases on
basic assumes, the ultimate limit state of HHPC-
HSR column was analyzed, some simply method
and factors were applied from the code for design of
concrete structure (GB50010-2010). So the normal
formulas of bearing capability for HPC-HSS column
with rectangle section were presented and were
shown as follow:
𝑁=𝛼
𝑓
𝑏𝜉ℎ
+𝑓
𝐴
−𝜎
𝐴
(1)
𝑁𝑒=𝛼
𝑓
𝑏𝜉ℎ
1−
+𝑓
𝐴
ℎ
−𝑎
(2)
In these formulas, the former was derived from
static balance on axial force, the later was
determined from moment balance. In these equations,
N was force perimeter or bearing capability; α
1
was
the shape coefficient,the value is 1 as concrete
strength is not more than C50, the value is 0.94 as
concrete strength is not less than C80,otherwise the
value is an interpolation between C50 and C80; f
c
is
compressed strength of concrete;for a rectangle
section,b is width, h
0
is effective height,ξ is relative
height; for steel bar, f’
y
is compressed strength and
A’
s
is section area of compressed yield failure, σ
s
is
stress and A
s
is section area of tensile or compress;e
is eccentric distance;a’
s
is a distance between force
point of compress area and compress edge of section.
2.3.2 Applicable Conditions in Analytic
Formulas
According to the conduct processes on equations (1)
and equation (2), some applicable conditions of
analytic equations were presented for HPC-HSR
column and were shown as the following:
• Bearing capability of axial compressed
column.In a word, the bearing capability of
eccentric compressed column was not more than
an bearing capability of axial compressed
column.For slender or moderate column,these
factors as buckling and second-order effect took
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
6

effect on the bearing capability, so the bearing
capability (N) of axial compressed column was
reduced by a buckling coefficient(φ) and was
shown as the following:
𝑁
≤
0
.
9𝜑
(𝑓
𝐴
+𝑓
𝐴′
)
(3)
Note: f
c
was compressed strength of high-
performance concrete, A
c
was section area of
concrete;f’
y
was compressed strength of high
strength steel bars.A’
s
was section area of steel bars.
φ was the buckling coefficient of axial-press bar and
defined according to the buckling coefficient from
GB50010-2010.
• Bearing capability of larger eccentric
compressed column.For rectangle section
column of HPC-HSS, a relative height of ξ was
not more than ξ
b
and the tension stress σ
s
of steel
bars was yield strength of f
y
in ultimate limit
state. So the equation (1) was simplified as the
equation (4), equation (2) and equation (4) were
applied for larger eccentric compressed column
of HPC-HSS.
𝑁=𝛼
𝑓
𝑏𝜉ℎ
+𝑓
𝐴
−𝑓
𝐴
(4)
• Bearing capability of small eccentric compressed
column.For rectangle section column of HPC-
HSS, a relative height of ξ was more than a limit
relative height of ξ
b
,the stress σ
s
of steel bars was
not more than yield strength in ultimate limit
state and shown as the following:
−𝑓′
≤𝜎
=𝑓
≤𝑓
(5)
Note: β
1
was shape coefficient of high-
performance concrete,the value is 0.8 as concrete
strength is not more than C50, the value is 0.74 as
concrete strength is not less than C80,otherwise the
value is an interpolation between C50 and C80.
3 PRACTISE CALCULATION
METHOD OF BEARING
CAPABILITY
3.1 Simplified Method of GB50010-
2010
Due to the variability and randomness of structural
loads, the RC members are primarily designed with
symmetric reinforcement. So 𝑓
=𝑓
or 𝐴
=𝐴
were applied in eccentric compressed column, the
equations (1), (3) for larger eccentric compressed
column could be solved directly according to
GB50010-2010, however an equation (6) for small
eccentric compressed column was derived form
these formulas and shown as the following:
𝑁𝑒
=𝛼
𝑓
𝑏ℎ
𝜉−
+𝑁−
𝛼
𝑓
𝑏ℎ
𝜉ℎ
−𝑎
(6)
As the equation (6), a cubic equation of ξ was
determined and could not be solved
directly.According to GB50010-2010, the second
order section of 𝜉(1−0.5𝜉)was simplified as
0.43,so a cubic equation was simplified as line
equation, the relative height ξ of compressed area
and reinforcement areas were shown as the
following:
𝜉=
.
+𝜉
(7)
𝐴
=𝐴
=
(8)
3.2 Precised Method from Cardano's
Formula
Let: 𝑁
=
; 𝑀
=
, then equation (6)
can be expressed as
𝜉
−𝜉
(
2+𝜉
)
+2𝜉𝜉
−1−
(
𝜉
−β
)
+
𝑀
+2𝑁
1 −
(
𝜉
−β
)
−2𝜉
𝑀
=0
(9)
The simplify calculation was derived form equation
(9) by substituting parameters and shown as:
• Determine some coefficients b, c, d.
b=−
(
2+𝜉
)
; c=2
𝜉
−
1−
(
𝜉
−β
)
+𝑀
;
𝑑=2𝑁
1 −
(
𝜉
−β
)
−2𝜉
𝑀
(10)
• Calculate some parameters p, q.
𝑝=−
; 𝑞=
;
(11)
• Calculate the relative height ξ of compressed
area.
𝜉=
−
+
+
+
−
−
+
−
(12)
Then the symmetric reinforcement area were
calculated by equation (12) and equation (8).
3.3 Simplified Method from Reduction
Order
According to simplified method of equation (6) from
GB50010-2010, the second order section of ξ(1-
0.5)ξ was reduced to the first order part of 0.25(1+ξ),
so the equation (6) was reduced as an second-order
Analytic Study on High-Performance Concrete Column with High-Strength Reinforcement Under Moment-Compress Loads
7
equation, then the relative height ξ of compressed
area was derived as:
𝜉=2B−
√
B
+C
(13)
In the equation (13), some parameters of B or C
were shown as;
B=𝑀
+
−1−
(
𝜉
−β
)
; 𝐶=
𝑁
1 −
(
𝜉
−β
)
−𝑀
𝜉
(14)
Then the symmetric reinforcement area were
calculated by equation (14) and equation (8).
4 VERIFICATION PROCESS ON
FORMULA OF BEARING
CAPABILITY
4.1 Evaluated Method on Calculated
Formulas of Bearing Capability
Some compressed tests on typical small eccentric
compression specimens were selected to verify the
formulas accuracy, including different reinforcement
strengths, concrete strengths, and geometric parameters.
First, the axial compressed force N
t
was a
bearing capability from some tests, the relative
height ξ of compressed area were calculated
according to the formulas of the papers and sample
parameters, then the bearing capability N
c
was
calculated according to the relative height ξ of
compressed area,section parameters of concrete and
reinforcement, strength parameters of construction
materials, finally the precision of calculation
formulas was evaluated by the ratio N
t
/N
c
between
the test bearing capability and the calculated bearing
capability. As the ratio was closed to 1, it means the
high precision of calculation formulas, otherwise it
means the less precision of calculation formulas.
4.2 Evaluated Examples of HPC-HSR
Column
4.2.1 HPC-HSR Column of
HRB500/HRBF500
Some members with C40 or C60 concrete and
HRB500/HRBF500 reinforcement were tested by
small eccentric compressed load. The bearing
capabilities of members were calculated by precise
method, simplified method of the code (GB50010-
2010) and simplified method of reduced order. The
formula accuracy on bearing capability of small
eccentric compressed specimens of
HRB500/HRBF500 reinforcement were analyzed as
Figure 1. the maximum deviation between simplified
method of the code and precise method exceeded
40%, however the relative deviation between
simplified method of reduced order and precise
method was smaller, some local deviations exceeded
20% for 𝑁
1. The calculation error of C40
specimens is smaller than that of C60 specimens.
(Mao, 2008).
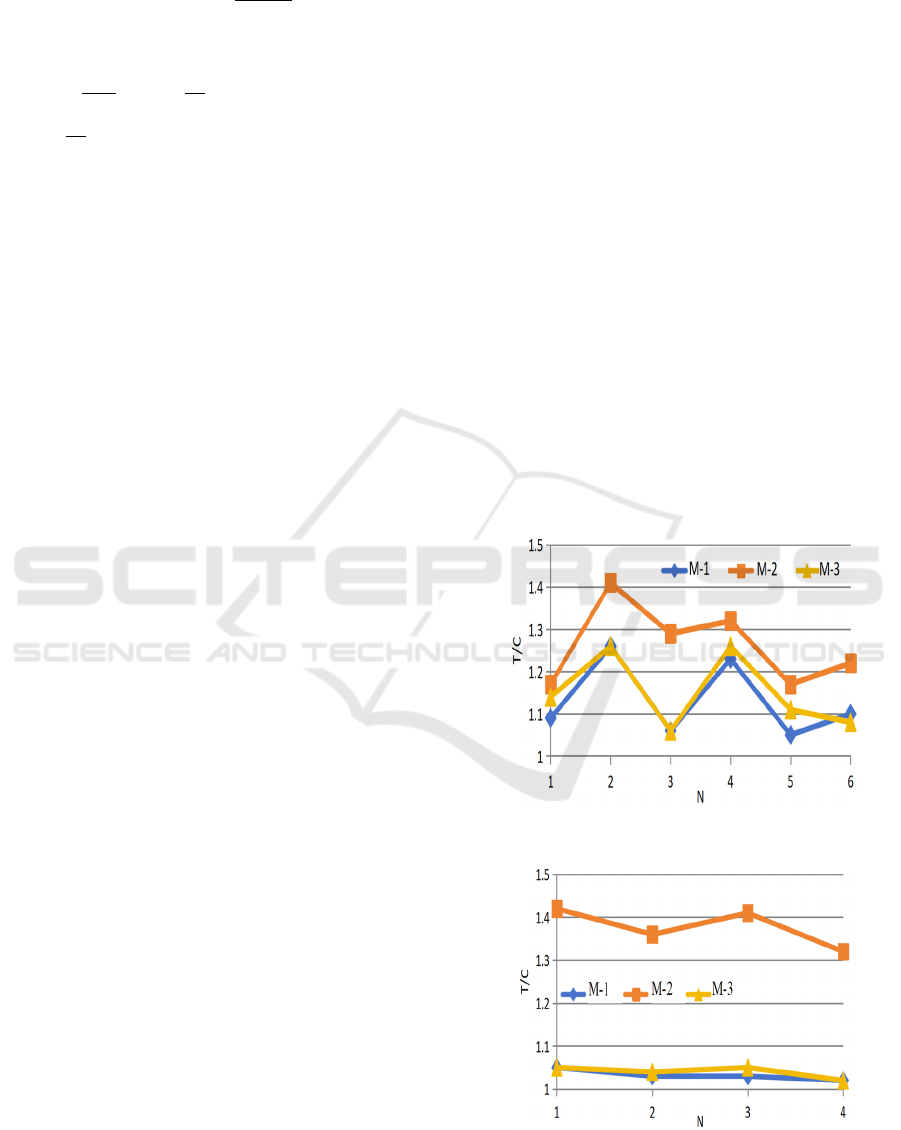
4.2.2 HPC-HSR Column of HRB630
Some members with C40 concrete and HRB630
reinforcement were tested by small eccentric
compressed load.The formula accuracy on bearing
capability of small eccentric compressed specimens
of HRB630 reinforcement were analyzed as Figure
2, the ratios of the test results and results from
precise method or simplified method of reduced
order were all around 1, the maximum ratio was
1.05. Then the accuracy of the formulas meet the
engineering requirements. However, the maximum
deviation of the results calculated by the code
formula exceeds 40%, the safety margin of the code
formula was larger. (Luo, 2013)
Figure 1: Column of HRB500 reinforcement.
Figure 2: Column of HRB500 reinforcement.
ICESCE 2024 - The International Conference on Environmental Science and Civil Engineering
8

Note: T was the result from tests, C was the
result from calculation; N was number of samples;
M-1 was the result from precised method of
Cardano's formula; M-2 was the result from the
simplified method of GB50010-2019; M-3 was the
result from the simplified method of reduced-order.
5 CONCLUSION
5.1 Formulas on Capability Bearing
and Reinforcement of HPC-HSS
Column
Two kinds of calculation formulas on capability
bearing and reinforcement are presented for HPC-
HSS column under small eccentric load. The former
is based on the Cardano formula for solving cubic
algebraic equations, and the calculated results have a
good degree of agreement with experimental
results.The latter is based on the reduction
processing of the original equation, the calculation
formula is simpler than the precise formula, but the
calculation accuracy is slightly worse. Both methods
proposed in this paper are consistent with the
experimental results and meet the accuracy
requirements for engineering calculations.
5.2 Influences of Slender Ratio and
Material Strength
Comparing the results of calculation formulas with
the experimental results of specimens with different
strength reinforcement, the precision of the
calculation results is significantly related to the
material strength.With the increase of material
strength , the bearing capability might be increased
for short HPC-HSS column.The optimal length of
HPC-HSS column and the minimum of bearing
capability were discussed for buckling and slender
ratio of slender or moderate column.
5.3 Deficiency and Reflection
Some influences were simplified and neglected, the
formulas might induce some deficiencies and
inaccuracy from test data. The formulas were
referenced to engineering design and analyzed to
some characters.The range of slender ratio should be
confirmed for the formula for buckling. The
calculation model of bearing capability might should
be more accurate on column with high-performance
concrete and high-strength reinforcement.
ACKNOWLEDGMENTS
The study was not financially supported.
REFERENCES
GB50010-2010. Code for design of concrete structures.
China Construction Press, Beijing. pp. 45-47. (In
Chinese)
ACI 318-19. 2019. Building Code Requirementsfor
Structural Concrete. American Concrete Institute,
Michigan. pp. 155-158.
Zhang, B., Qiu, L., Chen, X., et al., 2021. Study on
symmetric reinforcement calculation of rectangular
section column with HRB600 reinforcing bars under
eccentric compression. Building Structure 51(16):
116-120. (In Chinese)
Gao, Z., 2023. Experimental stuy on force performance of
630 MPA class high strength reinforced concrete
column. Hebei University of Technology, Tanjin. (In
Chinese)
Shen, Q., Wu, T., Wang, F., et al., 2024. Axially-
compressed behaviour of concrete columns reinforced
with novel high-strength steel-rebar materials: Testing,
modelling and design. Structures 70: 107841p1-18.
Ding, W., Deng, M., Li, T., et al., 2024. Experimental
study on eccentric compressive performance of RC
columns strengthened with textile-reinforced high-
strength high ductile concrete. Construction and
Building Materials 457: 1393821p1-13.
Jia, P. C., Wu, H., Peng, Q., et al., 2024. Dynamic
behaviors of eccentrically loaded RC column under
lateral low-velocity impact. Engineering Structures
309: 118031p1-21.
Ma, L.-C., Shi, Q.-X., Wang, P., et al., 2024. High
strength reinforced column monotonic load test
eccentric compression performance design method.
Engineering Mechanics 41(3): 82-90. (In Chinese)
Mao, D., 2008. Research on mechanical properties of
reinforced concrete compressive members at 500Mpa
reinforcement. Zhengzhou University, ZHENGZHOU.
(In Chinese)
Luo, S., 2013. Experimental study on the mechanical
properties of eccentrically compressed members of
reinforced concrete with 600Mpa grade reinforcement.
Southeast University, Nanjing. (In Chinese)
Analytic Study on High-Performance Concrete Column with High-Strength Reinforcement Under Moment-Compress Loads
9
