Exploring the Impact of Data Heterogeneity in Federated Learning

for Fraud Detection

Zhiqiu Wang

Computer Science, ShanghaiTech University, Shanghai, China

Keywords: Federated Learning, Logistic Regression, Decision Tree, Random Forest.

Abstract: With the increase of credit card utilization rate, credit card fraud cases are increasing, which has gradually

become an important problem that people need to solve. This study examines the overall effectiveness of the

three Machine Learning (ML) methods, proposes a federated learning algorithm integrated with three separate

ML methods, and discusses the algorithms' performance in the face of varying degrees of data heterogeneity.

The study uses a Kaggle dataset that included information on about 550,000 credit card trades made by

cardholders across Europe. By using K-means algorithm to simulate different degrees of heterogeneity in data,

ML methods such as Logistic Regression, Decision Tree and Random Forest are respectively used to embed

the framework of federated learning. Each model was applied to these data with varying degrees of

heterogeneity for fraud identification of credit card transactions. The results show that federal learning

algorithms still face challenges when faced with data with strong data heterogeneity. The performance of

Logistic Regression and Decision Tree method is more stable, while the performance of Random Forest

method is more volatile.

1 INTRODUCTION

Credit cards are an effective tool for expanding

domestic demand, promoting consumption, and

driving economic growth. In recent years, there has

been a continual growing in the number of bank

accounts, non-cash payment transactions, and

payment system transactions, all of which are

expanding on an already substantial foundation. In

recent years, with the development of the times, the

number of bank accounts, non-cash payment

transactions, and payment system transactions have

all continued to grow, even on an already large base.

Additionally, the transaction volume of bank cards

has steadily increased, and the scale of credit card

loans has expanded. However, along with the rapid

development of credit card payments, some issues

have emerged, such as certain banks focusing solely

on increasing the number of credit cards while

neglecting customer management. Bank customers

may face risks like personal information leaks and

credit card fraud. As mobile payments become more

widespread, credit card payment methods continue to

https://orcid.org/0009-0005-3551-4858

evolve, and credit card fraud techniques are also

becoming more sophisticated. Addressing the risks of

fraud and combating online financial crime will

present new challenges.

In the past, people often failed to realize they were

victims of credit card fraud in time to take measures

to protect their assets. Nowadays, bank systems may

have chances to detect potential fraud by installing

credit card fraud detection programs. When fraud is

suspected, a signal is sent to the bank, allowing it to

take preventive actions. For example, customers may

be required to visit a physical branch in person to

withdraw or transfer funds, thus reducing the risk of

falling victim to fraud. As the information era has

progressed, so too have the number of academics

studying fraud detection, and notable strides have

been made. In order to discover anomalies in

consumer electronics, Bhowmik et al., for example,

created Quantum Machine Learning (QML), which

combines the capabilities of quantum computing,

quantum information, and ML techniques (Bhowmik

et al., 2024)., Martins et al. proposed Inducing Rules

for Fraud Detection from Decision Trees (RIFF), a

418

Wang and Z.

Exploring the Impact of Data Heterogeneity in Federated Learning for Fraud Detection.

DOI: 10.5220/0013525200004619

In Proceedings of the 2nd International Conference on Data Analysis and Machine Learning (DAML 2024), pages 418-422

ISBN: 978-989-758-754-2

rule induction algorithm that extracts a low False

Positive Rate (FPR) rule set directly from decision

trees in fraud detection (Martins et al., 2024), Lu et

al. evaluate the applicability of Kolmogorov-Arnold

Networks (KAN) applied in fraud detection, by

proposing a rapid decision rule based on Principal

Component Analysis (PCA) to evaluate the

appropriateness of KAN, along with introducing a

heuristic method for hyperparameter tuning, finding

that their effectiveness is context-dependent (Lu et

al., 2024). However, there is limited research that

simultaneously focuses on improving fraud detection

accuracy while considering the protection of user

privacy.

Therefore, this paper will conduct a more in-depth

discussion on fraud detection under the premise of

safeguarding user privacy. A dataset related to credit

card fraud detection on Kaggle was employed. This

study first used the K-means algorithm to classify the

dataset, and then simulated the Non-Independent and

Identically Distributed (non-iid)) characteristics of

the data by assigning data from the same category to

a single client. This paper also simulated the

Independent and Identically Distributed (iid)

characteristics by evenly distributing data from

different categories to each client. This setup is used

to compare the performance of the FedAvg algorithm

with embedded Logistic Regression model when

dealing with these two types of data distributions.

2 METHODS

2.1 Data Preparation

The data set used came from the website 'Kaggle'

(Elgiriyewithana, 2023), which contains more than

550,000 credit card trades made by European credit

card holders in 2023. The main features of this dataset

are V1-V28, processed with dimension reduction

methods by the author. Finally, the data set's label

(Class) is binary, indicating that the transaction is

either a credit card fraud (1) or not a fraud (0).

In terms of the data preprocessing, first, the id and

label columns are discarded from the dataset. Since

the Amount feature and the other features (V1-V28)

have significant differences in their value ranges, this

study applies standardization to the other features.

The dataset is splitted for training and testing in 8:2.

To investigate the impact of non-iid data on the

federated learning algorithm, K-means clustering is

applied to the training set, dividing it into clusters

corresponding to the number of clients. Each cluster

is then assigned to a corresponding client, simulating

the non-iid nature of the data. To simulate iid data,

each cluster is evenly distributed among the clients.

The performance of three ML algorithms—

Decision Trees, Random Forests, and Logistic

Regression—integrated into a federated learning

framework for a binary classification task is

investigated in this paper. After multiple rounds,

which can be determined by the variable

‘num_communications’, of training and

communication between clients, a global model is

obtained by combining the models from multiple

clients. This global model is then used to make

predictions on the test set. Accuracy, which is

computed as the ratio of properly categorized samples

to the total number of samples, is used to assess the

performance of the model.

2.2 Federated Learning-based Machine

Learning Models

Federated Learning, also known as Federated

Machine Learning, is a method proposed to address

privacy issues during joint model training (Li et al.,

2020; Mammen, 2021). In this approach, each

organization trains its own model locally. After

completing the training, each organization uploads its

model parameters to a central server (or it can be peer-

to-peer). The central server combines the parameters

from different organizations (this can be done by

uploading gradients or updated parameters) and

recalculates new parameters (e.g., through weighted

averaging, a process known as federated

aggregation). These new parameters are then

distributed back to each organization, which deploys

them into their models to continue further training.

This process can be repeated iteratively until the

model converges or other predefined conditions are

met. The study mainly focusses on the relation

between the variable ‘num_client’ (the number of

clients in the federated learning) and accuracy of the

test data. Experiments are conducted based on

‘num_clients’ disparately equals to 2,4,6,8. Other

hyper-parameters are fixed, in which ‘learning_rate’

(the step size) equals to 0.01, ‘num_communications’

(the number of communication rounds) equals to 10,

‘num_local_steps’ (the number of local steps clients

take in each communication round) equals to 8.

Exploring the Impact of Data Heterogeneity in Federated Learning for Fraud Detection

419

2.2.1 Logistic Regression

The algorithm calculates the output probability for a

given input variable using a parametric function

known as the sigmoid function. The likelihood that a

sample is in the positive class is represented by the

value between 0 and 1, which is the result of mapping

the linear combination of the input variables

(LaValley, 2008; Nick et al., 2007).

The training process involves estimating the

model weights by maximizing the likelihood

function, a function of the model parameters,

indicating the probability of the samples given the

model. When this algorithm is embedded into the

federated learning framework, each client performs

local training for a specific number of local steps.

Once local training is complete, the trained

coefficients are sent to the central server. The server

then averages these coefficients and sends the

updated values back to each client.

2.2.2 Random Forest

It consists of a “forest” of decision trees, where each

tree is independently trained on a random subset of

samples drawn from the original training set (Rigatti,

2017). Finally, the random forest combines the output

of all decision trees, and this study uses the majority

voting principle to determine the final predicted

class.Unlike the logistic regression algorithm,

although the random forest model does not have

explicit parameters that can be averaged, the

aggregation concept in federated learning can still be

realized by merging decision trees from client models

and randomly sampling to generate a global model.

The specific implementation steps are as follows:

each client independently trains a random forest

model (without sharing data). After each

communication round, the server collects the random

forest models from each client, merges all the

decision trees, and then randomly samples

n_estimators trees from the combined model to form

a new global model. The server then distributes the

updated global model to the clients for the next

training round. This approach allows for the client

models to be "merged" through the global model,

even though the data is not exchanged directly.

2.2.3 Decision Tree

A decision tree performs decision analysis using a

tree structure in classification tasks (Song et al.,

2015). It follows a top-down recursive approach,

starting from the root node, where attribute values are

compared at internal nodes, and based on the

comparison results, samples are assigned to different

child nodes until reaching a leaf node, which

represents the final classification outcome. Each node

of the decision tree represents an object, the branches

represent possible classification attributes, and each

leaf corresponds to the value of the object as

determined by the path from the root node to that leaf.

Although decision tree models cannot be as easily

averaged as linear models, federated learning can still

be achieved while preserving data privacy by

effectively aggregating the models uploaded by each

client. During model aggregation, the study selects

parts of the subtree nodes from each client’s decision

tree model (choosing decision tree models with

greater depth) to combine the decision tree models.

Similarly, after each communication round, the

clients independently train their respective decision

trees and send these models back to the server. The

server then aggregates parts of these models’

structures using the aforementioned strategy to

generate a new global decision tree model.

3 RESULTS AND DISCUSSION

3.1 Performance of Data with Varying

Degrees of Heterogeneity

This study conducted experiments based on federated

learning with three machine learning models, with

'num_client' set to 2, 4, 6, and 8 (where the data is

divided into 'num_client' categories during

preprocessing; a larger 'num_client' indicates greater

data heterogeneity).

3.1.1 Logistic Regression Based Federated

Learning

Under an IID data distribution, Figure 1 demonstrates

that test accuracy rises as the number of clients grows.

This implies that a larger number of clients provides

the model with more data, enabling it to extract more

useful information. However, in the case of Non-IID

data distribution, test accuracy declines as the number

of clients increases. This indicates that adding more

clients exacerbates data imbalance, making it more

challenging for the model to learn effectively and

resulting in a decrease in its generalization capability.

DAML 2024 - International Conference on Data Analysis and Machine Learning

420

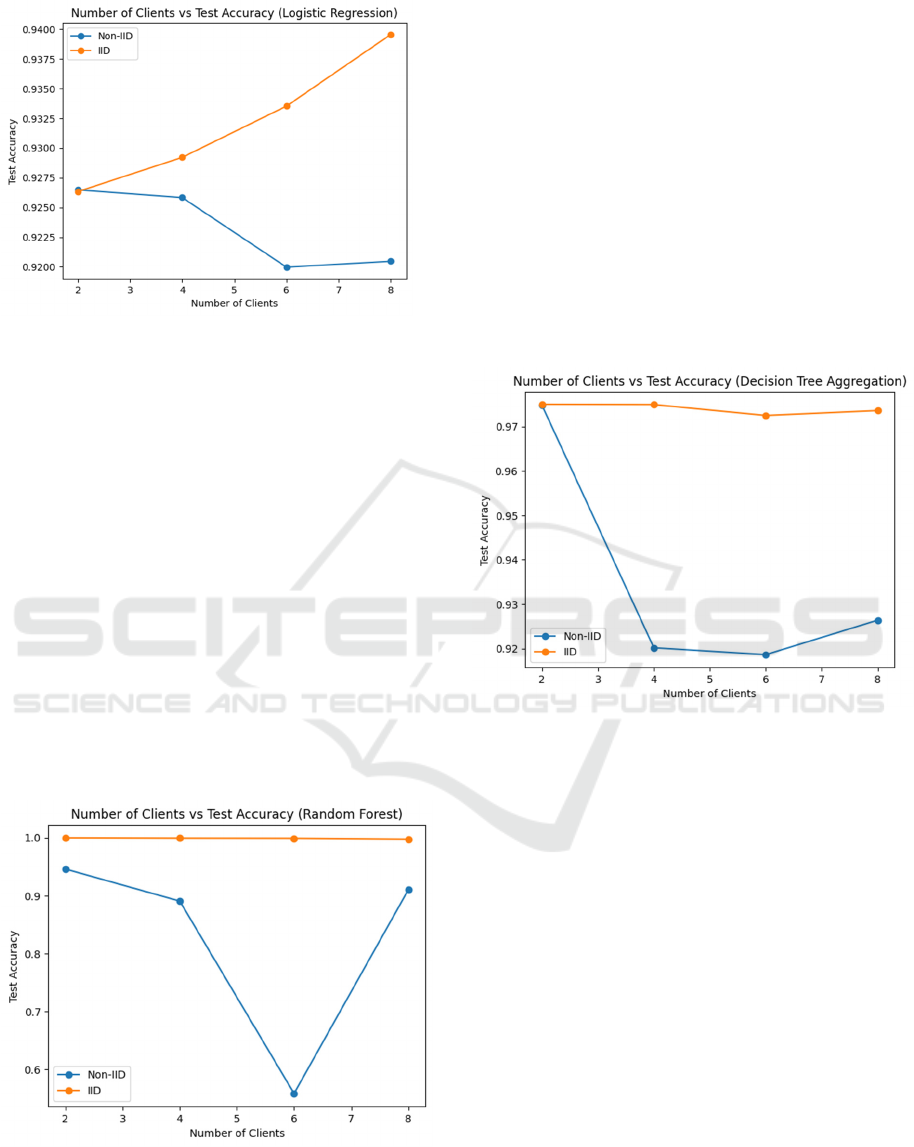
Figure 1: The influence of Number of Clients in Test

Accuracy based on Logistic Regression model

(Photo/Picture credit: Original).

3.1.2 Random Forest Based Federated

Learning

In the case of IID data distribution, as shown in Figure

2, the test accuracy remains relatively steady with

only slight fluctuations as the number of clients

increases. In contrast, under a Non-IID data

distribution, test accuracy tends to decline as the

number of clients rises, with performance becoming

highly unstable, particularly hitting a low point with

six clients. This suggests that Non-IID data

distribution significantly affects model performance.

The random forest trees may prioritize certain

features from specific clients, causing overall

performance instability and a marked drop in

accuracy with six clients.

Figure 2: The influence of Number of Clients in Test

Accuracy based on Random Forest model

(Photo/Picture credit: Original).

3.1.3 Decision Tree Based Federated

Learning

Under an IID data distribution as shown in Figure 3,

test accuracy stays relatively stable with only small

fluctuations as the number of clients growings,

suggesting that the decision tree can successfully

capture the overall data characteristics. However,

with a Non-IID data distribution, test accuracy

generally declines as the number of clients grows, and

there are noticeable fluctuations. Since decision trees

rely heavily on local data distribution, significant

differences in client data under Non-IID conditions

can cause the trees to favor different branches,

resulting in decision errors or increased model bias.

Figure 3: The influence of Number of Clients in Test

Accuracy based on Decision Forest model

(Photo/Picture credit: Original).

3.2 Performance of Different Machine

Learning Models

As shown in Table 1, the test accuracy of logistic

regression is relatively stable, with minimal

fluctuations across different numbers of clients. This

indicates that the Logistic Regression model exhibits

strong robustness to Non-IID data and possesses high

generalization ability. In contrast, the effectiveness of

the Random Forest model becomes highly unstable as

the number of clients increases, with accuracy

dropping sharply to 55.85% when there are six

clients. This may be due to the extreme data

distribution in some clients, leading to overfitting in

certain decision trees within the random forest,

resulting in poor generalization and significant

performance fluctuation. The test accuracy of the

decision tree model is also relatively stable with slight

fluctuations across different numbers of clients.

Exploring the Impact of Data Heterogeneity in Federated Learning for Fraud Detection

421

Although there is a slight decline at six clients, the

overall test accuracy does not vary significantly,

indicating that the decision tree model maintains a

certain level of stability in handling local data

distributions.

Table 1: Accuracy of different number of clients in different

models

4 CONCLUSION

This study utilized three different machine learning

models embedded in a federated learning framework

to classify credit card transactions as fraudulent or

not. By using the K-means algorithm to cluster data,

varying degrees of data heterogeneity were simulated

to explore the performance and behavior of each

algorithm under such conditions, as well as to

compare them against each other. The ML models

used were Logistic Regression, Random Forest, and

Decision Tree. Among them, Logistic Regression and

Decision Tree demonstrated more stable performance

against changes in data heterogeneity (with Logistic

Regression having the highest overall test accuracy),

while the Random Forest model showed greater

fluctuation. In the future, through more extensive

research and exploration, it may be possible to find

federated learning models and methods that offer

higher accuracy and stability when dealing with

highly heterogeneous data, while also ensuring user

privacy protection.

REFERENCES

Bhowmik, S., & Thaplival, H. 2024. Quantum machine

learning for anomaly detection in consumer electronics.

In 2024 IEEE Computer Society Annual Symposium on

VLSI (ISVLSI) (pp. 544-550). IEEE.

Elgiriyewithana. 2023. Credit card fraud detection dataset.

Retrieved from

https://www.kaggle.com/datasets/nelgiriyewithana/cre

dit-card-fraud-detection-dataset-2023/data

LaValley, M. P. 2008. Logistic regression. Circulation,

117(18), 2395-2399.

Li, L., Fan, Y., Tse, M., & Lin, K. Y. 2020. A review of

applications in federated learning. Computers &

Industrial Engineering, 149, 106854.

Lu, Y., & Zhan, F. 2024. Kolmogorov Arnold networks in

fraud detection: Bridging the gap between theory and

practice. arXiv preprint arXiv:2408.10263.

Mammen, P. M. 2021. Federated learning: Opportunities

and challenges. arXiv preprint arXiv:2101.05428.

Martins, L., Bravo, J., Gomes, A. S., Soares, C., & Bizarro,

P. 2024. RIFF: Inducing rules for fraud detection from

decision trees. In International Joint Conference on

Rules and Reasoning (pp. 50-58). Cham: Springer

Nature Switzerland.

Nick, T. G., & Campbell, K. M. 2007. Logistic regression.

Topics in Biostatistics, 273-301.

Rigatti, S. J. 2017. Random forest. Journal of Insurance

Medicine, 47(1), 31-39.

Song, Y. Y., & Ying, L. U. 2015. Decision tree methods:

Applications for classification and prediction. Shanghai

Archives of Psychiatry, 27(2), 130.

Model Name The number of clients

4 6 8

Logistic

Regression

92.58 92.00 92.05

Random Forest 89.05 55.85 91.01

Decision Tree 92.02 91.86 92.64

DAML 2024 - International Conference on Data Analysis and Machine Learning

422