Survival Analysis of the Titanic Using Random Forests

Tianchong Tang

College of Information Science and Engineering, Ocean University of China, San Sha Street, Qing Dao, China

Keywords: Random Forest, Survival Analysis, Machine Learning.

Abstract: The Titanic disaster is one of the most widely studied maritime tragedies. Analyzing passenger survival rates

has become a hot topic. This research endeavors to forecast the likelihood of survival among Titanic voyagers

by employing a random forest algorithmic approach. The datasets employed in this analysis include features

such as PassengerId, Survived, Pclass, Name, Sex, Age, SibSp, Parch, Ticket, Fare, Cabin, and Embarked.

To enhance prediction performance, the author implemented a random forest algorithm, which integrates

multiple decision trees. Following data preprocessing, the dataset was randomly separated into a training set,

comprising 80%, and a test set, constituting 20%. Across 500 distinct iterations, the data was randomly split

into training and test sets. The random forest model achieved an average accuracy of 0.8013, demonstrating

its effectiveness in assessing the likelihood of Titanic voyagers' endurance. This underscores the considerable

potential of the random forest algorithm in conducting survival analyses.

1 INTRODUCTION

The Titanic was not only an engineering marvel of its

time but also a focal point for numerous studies and

discussions. The accident killed about 1,500

people. To enhance disaster response capabilities,

researchers began utilizing machine learning

techniques to predict passengers' survival

probabilities. In addition to the work by (Gleicher and

Stevans 2004), who employed logistic regression

models to analyze key factors such as gender and age,

researchers gradually recognized that social status

might also influence survival chances. For instance, a

passenger's cabin class and royal status could garner

support from fellow travelers in critical moments,

thereby improving survival odds. Furthermore,

research has demonstrated the successful application

of generalized linear models and decision tree

algorithms (distinct from the algorithms discussed in

this paper) (Durmuş and Güneri, 2020). For data

processing, there are also studies that have created

many new features, such as "child", "new_fare",

"FamilyIdentity", etc. (Datla, 2015), which are

different from the feature engineering in this paper.

In the study of Nadine Farag and Ghada Hassan, the

accuracy of the naive Bayes model even reached

92.52% (Farag and Hassan, 2018). There are also

some studies that predict the survival risk of Titanic's

passengers through statistical scoring methods (Ligot,

2022), which can divide passengers into different risk

levels, unlike machine learning. Historically, survival

analysis has relied on statistical methods, including

the Cox proportional hazards model (Cox, 1972) and

the Kaplan-Meier estimator (Kaplan and Meier,

1958). This paper delves into survival analysis of

Titanic passengers using the random forest method.

The article initially explicates the fundamental tenets

underlying the random forest model, subsequently

outlines the preprocessing procedures applied to the

original Titanic data collection, and ultimately

ascertains the precision of the random forest model.

This exemplifies the potentiality of machine learning

in the scrutiny of survival percentages. The

discussion section first introduces decision trees,

which are a key component of the random forest, then

analyzes the optimal decision tree from the

perspective of information gain, and finally concludes

by integrating decision trees into a unified random

forest framework.

120

Tang and T.

Survival Analysis of the Titanic Using Random Forests.

DOI: 10.5220/0013510300004619

In Proceedings of the 2nd International Conference on Data Analysis and Machine Learning (DAML 2024), pages 120-123

ISBN: 978-989-758-754-2

2 THE PRINCIPLE OF RANDOM

FOREST

2.1 The Basic Principles of Decision

Tree Generation

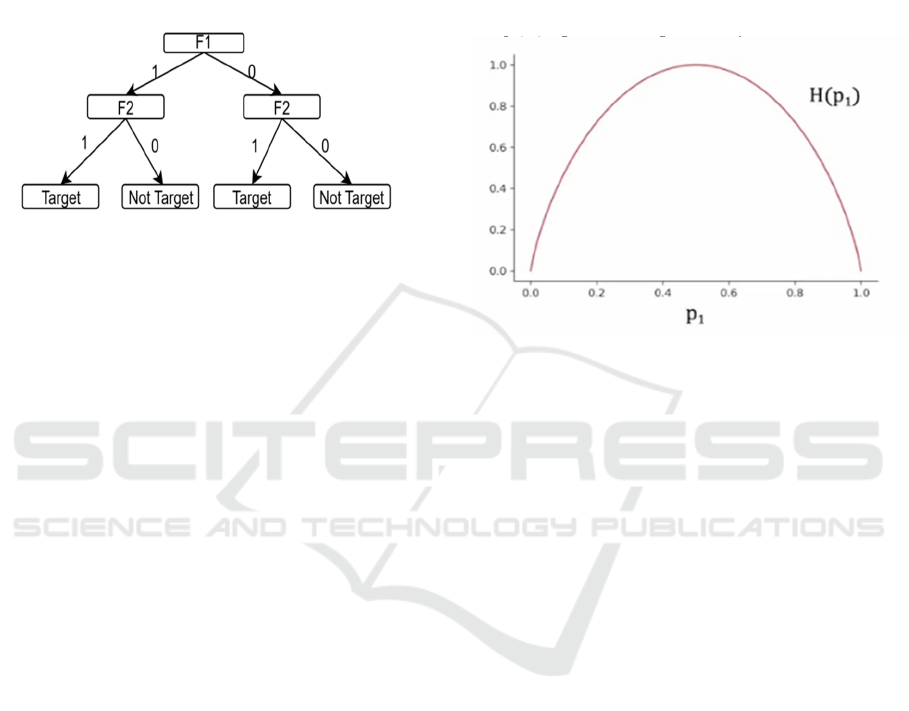
Figure 1:Sample decision tree based on binary target

variable Y (Picture credit : Original)

Figure 1 illustrates a basic decision tree model

utilized for classification tasks. At the beginning of

the decision tree (at the top), the initial classification

of samples occurs based on a specific feature, known

as the root node. In this instance, samples can be

divided into those with F1=1 and those with F1=0.

Subsequently, further classification happens through

internal nodes, until the final feature is evaluated.

There may be instances where further classification is

unnecessary, as samples at that point belong to a

single category. In such cases, there is no need for

additional classification since only one type of sample

remains in that node. Conversely, even after

classifying through all the designated features, some

nodes may contain samples from multiple categories.

When this occurs, the nodes that cannot be further

classified are referred to as leaf nodes. Often, these

leaf nodes contain a mix of different samples. If the

disparity between the sizes of the two sample types is

minimal, it complicates predictions derived from this

decision tree. This indicates that the decision tree

created based on the sequence of these features may

not be optimal. A potential next step could involve

utilizing F2 as the new root node for classification.

The problem is addressed using information entropy.

The following section delves into the process of

obtaining an ideal decision tree. It is important to

keep in mind that in cases where the dataset contains

numerous attributes, the creation of a decision tree

can become intricate if each attribute is taken into

account. By leveraging information entropy, a

determination can be made on whether further

bifurcation should be pursued.

2.2 Information Gain

Information entropy is used to indicate the degree of

inconsistency in information (Shannon, 1948). The

formula for calculating information entropy is:

HX = 



px



log



px









(1)

px



represents the probability of a random event.

Figure 2: Image as a function of information

entropy(Picture credit : Original)

Figure 2 is a function of information entropy, and

when the number of target and non-target samples is

about the same, the prediction accuracy is low and the

information entropy is large. Not an ideal decision

tree. In the presence of a substantial disparity in the

count of target versus non-target exemplars, the

predictive precision is elevated and the entropy of

information is diminished This is an ideal decision

tree.

Information Gain is a metric used to measure the

information contribution of a feature to a dataset

(Shannon, 1948). The basic idea is how much the

information uncertainty (entropy) of the dataset is

reduced when it is divided by a certain feature. The

weighted average information entropy of different

branches in the decision tree divided by different

feature order is used to obtain the final weighted

average information entropy. The decision tree with

the least weighted information entropy is the most

ideal decision tree. Let the author gives a more

detailed explanation. Distribute the count of

exemplars pertaining to each root node by the overall

exemplar count, multiply the resultant by its

respective entropy of information, and add up these

values to the weighted mean entropy of information.

By comparing the weighted average information

entropy, the decision tree with the highest accuracy

can be obtained, that is, the optimal decision tree.

Survival Analysis of the Titanic Using Random Forests

121

2.3 Random Forest

The random forest performs put-back sampling of the

initial samples, and train the decision tree from the

samples after each put-back sampling (Breiman,

2001). Specifically, a random forest takes one sample

out of the initial n samples as the first sample of a new

sample. In the next sampling, the previous sampled

items are still taken into consideration. This means

that the samples that have been drawn before may still

be selected again. There are n new samples that are

taken back to the sampling plot n times, and the

obtained n new samples are used to train a decision

tree. Then train the next decision tree in the same way.

The quantity of decision trees is adjustable. Typically,

as the count of decision trees increases, the efficacy

of the random forest model improves. However,

training too many decision trees can lead to too long

training times. Too little training for decision trees

makes it difficult to reduce the impact of noise. The

number of decision trees is generally 64 to 228.

Modify the count of decision trees according to the

model's performance, iterating until the optimal

random forest model is constructed.

The prediction accuracy formula is:

a =





(2)

Where a is the prediction accuracy, t is the number

of samples correctly predicted, and s is the sum of the

samples. The results a are rounded.

3 RESULTS

In Table 1, the initial six entries of the dataset are

illustrated. This dataset comprises a total of 893

records, featuring twelve attributes: PassengerId,

Survived, Pclass, Name, Sex, Age, SibSp, Parch,

Ticket, Fare, Cabin, and Embarked. PassengerId is

only used as an identifier, so it can be disregarded.

The processing of the data is as follows:

1.Sex, Pclass, Embarked data categories are

minimal. Different numbers represent different

categories of data. For example, in the Sex feature,

female is 1 and male is 0.

2.The Age feature is incomplete, so it is filled in

with the median value calculated from the

combination of the Sex feature and PClass feature.

3. For continuous data such as Age and Fare, set to

4 appropriate intervals and use different numbers to

represent different intervals. It is worth noting that

since there are very few people with an age greater

than 64, the data with an age greater than 64 are not

processed.

4.Merge the SibSp and Parch features into an

IsAlone feature. If SibSp and Parch are added

together to 0, then IsAlone is 0, otherwise it is 1.

5.Change the Name feature to the Title feature

according to its characteristics, and also use different

numbers to represent different data types. If the Name

contains Mr, it is 1 in the Title. If the Name contains

the Master, it is 4 in the Title.

6. Because the filling of Age features is related to

PClass features, leading to the creation of a combined

Age*Class feature.

The writer partitioned the dataset into two subsets:

a training set and a test set, allocating 80% for the

purpose of training and retaining 20% for testing.

Table 1: Example dataset.

PassengeId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cab

Emba

rke

1 0 3 Braund, Mr. Owen

Harris

male 22 1 0

A/5

21171

7.25 S

2 1 1 Cumings, Mrs.

John Bradley

(Florence Briggs

Thayer)

female 38 1 0

17599

71.2833 C85 C

3 1 3

Heikkinen, Miss.

Laina

female 26 0 0

STON/

O2.

310128

7.925 S

4 1 1 Futrelle, Mrs.

Jacques Heath (Lily

May Peel)

female 35 1 0 113803 53.1

C12

5 0 3 Allen, Mr. William

Henr

male 35 0 0 373450 8.05 S

6 0 3 Moran, Mr. James male 0 0 330877 8.4583 Q

DAML 2024 - International Conference on Data Analysis and Machine Learning

122

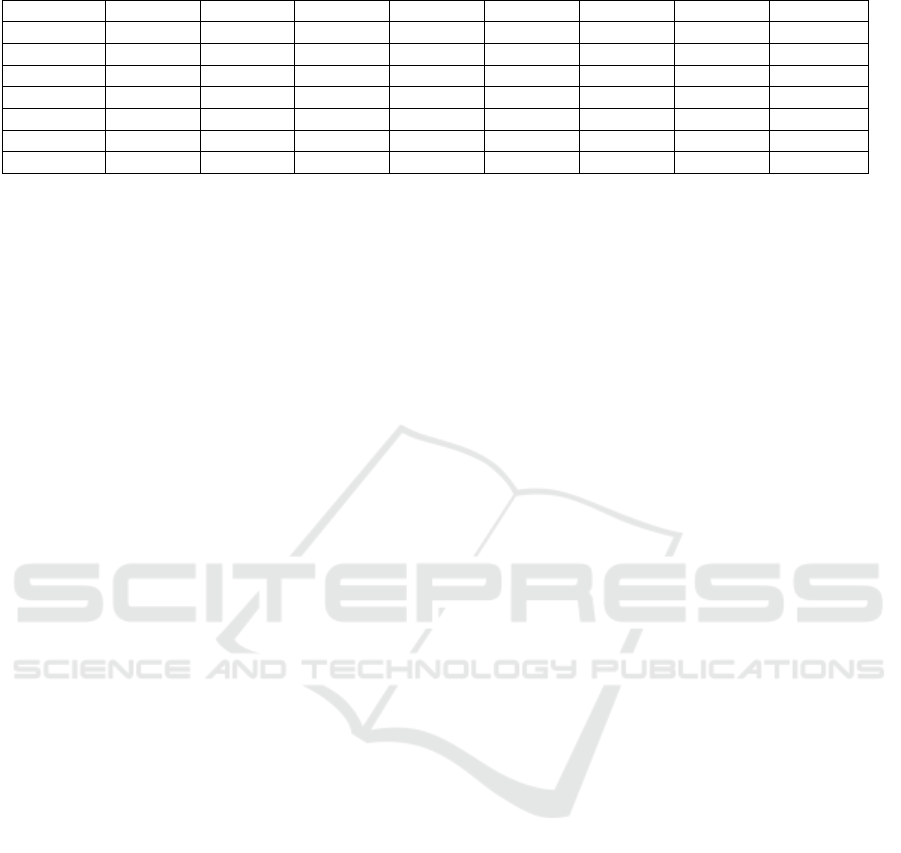
Table 2: Processed example dataset.

Passen

Pclass Sex A

e Fare Embarke

Title IsAlone A

e*Class

892 3 0 2 0 2 1 1 6

893 3 1 2 0 0 3 0 6

894 2 0 3 1 2 1 1 6

895 3 0 1 1 0 1 1 3

896 3 1 1 1 0 3 0 3

897 3 0 0 1 0 1 1 0

898 3 1 1 0 2 2 1 3

Table 2 displays the Processed sample dataset,

which is utilized to train the random forest model and

analyze the training information (100 decision trees

were employed by the author). To minimize errors

stemming from the random selection of both training

and test data, the researchers randomly picked data

500 times and trained them to determine the

predictive accuracy. By averaging these values, the

mean predictive accuracy obtained was 0.8013.

4 CONCLUSIONS

This study reveals that the Random Forest algorithm

achieved a high level of predictive accuracy of

survival rates on the Titanic dataset, reaching 0.8013

(Eighty percent of the initial dataset is employed in

the training subset, whereas twenty percent is

reserved for the testing subset. The original dataset is

randomly divided into 500 subsets to calculate the

average test accuracy). This outcome exemplifies the

benefits of utilizing random forest models for

predicting survival rates, particularly in scenarios

involving numerous features and intricate

interrelations. There is still potential for improvement

in data processing in current research. Additionally,

The precision of survival forecasting can be

augmented further through the utilization of

alternative model evaluations or the amalgamation of

diverse models. Future studies will likely make

progress in this area.

REFERENCES

Breiman, L., 2001. Random forests. In Machine

learning, 45, 5-32.

Cox, D. R., 1972. Regression models and life‐tables. In

Journal of the Royal Statistical Society: Series B

(Methodological), 34(2), 187-202.

Datla, M. V., 2015. Bench marking of classification

algorithms: Decision Trees and Random Forests-a case

study using R. In 2015 international conference on

trends in automation, communications and computing

technology (I-TACT-15) (pp. 1-7). IEEE.

Durmuş, B., Güneri, Ö. İ., 2020. Analysis and detection of

Titanic survivors using generalized linear models and

decision tree algorithm. In International Journal of

Applied Mathematics Electronics and Computers, 8(4),

109-114.

Farag, N., Hassan, G., 2018. Predicting the survivors of the

Titanic Kaggle, machine learning From disaster.

In Proceedings of the 7th international conference on

software and information engineering (pp. 32-37).

Gleicher, D., Stevans, L. K., 2004. Who survived Titanic?

A logistic regression analysis. In International Journal

of Maritime History, 16(2), 61-94.

Kaplan, E. L., Meier, P., 1958. Nonparametric estimation

from incomplete observations. In Journal of the

American statistical association, 53(282), 457-481.

Ligot, D. V., 2022. Developing a Titanic Survival

Scorecard: Risk Analysis of Populations Through

Statistical Scoring Methods. Available at SSRN

4015684.

Shannon, C. E., 1948. A mathematical theory of

communication. In The Bell system technical

journal, 27(3), 379-423.

Titanic_data, 2024.

https://www.kaggle.com/competitions/titanic/data

Survival Analysis of the Titanic Using Random Forests

123