Evaluating the Generalizability of Machine Learning Models for

Seismic Data Prediction Across Different Regions

Yuning Cai

Crestwood Preparatory College, Toronto, Canada

Keywords: Machine Learning, Earthquakes, Prediction, Generalizability.

Abstract: Earthquake prediction is a critical challenge, requiring advanced methods with strong generalization

capabilities. This paper investigates the generalization of traditional machine learning models—Linear

Regression (LR), Support Vector Regression (SVR), Random Forest (RF), K-Nearest Neighbors (KNN), and

Decision Tree (DT)—in predicting earthquake magnitudes across different geographic distributions. Using

seismic data from the United States Geological Survey (USGS), the study trains models on data from the

Eastern Hemisphere and tests them on the Western Hemisphere, evaluating their performance and ability to

migrate across regions. The RF model showed superior generalization with the lowest mean squared error

(MSE) and the highest R² value, indicating robust performance across different distributions. In contrast, the

KNN model struggled, reflecting its limitations in handling diverse data. The study's findings demonstrate the

reliability of RF in generalizing across distributions and the significance of model selection when working

with information from various geographic areas. More comprehensive knowledge of model migration and its

adaptability to various datasets is facilitated by this work, opening the door for more trustworthy earthquake

prediction models.

1 INTRODUCTION

Natural disasters have always posed significant

threats to human life, infrastructure, and the

environment. Among these disasters, earthquakes are

among the most destructive due to their sudden

occurrence and devastating impacts. An earthquake is

typically caused by the rapid release of energy in the

Earth's crust, usually due to tectonic activities like

fault slips. Earthquakes can trigger secondary hazards

such as tsunamis, landslides, and building collapses,

which amplify the risks to human populations (Duan,

2021; Mavrouli, 2023). Given the frequency and

severity of seismic events, the ability to predict

earthquake magnitudes is crucial for early warning

systems and risk mitigation strategies.

However, traditional earthquake prediction

methods, primarily based on seismological data

analysis and empirical models, have significant

limitations. These methods often struggle with

accurately predicting the timing, location, and

magnitude of seismic events due to the highly

complex nature of geological processes (Wald, 2020;

https://orcid.org/0009-0007-2095-8450

Mignan, 2020). With advancements in computational

technology, there is increasing interest in using

Artificial Intelligence (AI) techniques to improve

prediction accuracy and address these challenges. AI

models, leveraging large datasets and sophisticated

algorithms, have shown promise in capturing non-

linear patterns. Combining AI with seismological

data could enhance earthquake prediction

capabilities, making this field an essential area of

exploration (Banna, 2020; Bhatia, 2023).

AI has rapidly evolved over the past few decades

and has been successfully applied in various domains,

ranging from healthcare and finance to environmental

monitoring and disaster management (Secinaro,

2021; Goodell, 2021; Ullo, 2020; Sun, 2020).

Representative machine learning algorithms have

demonstrated impressive performance in complex

tasks, including pattern recognition, time-series

forecasting, and anomaly detection (Pisner, 2020;

Aguilar, 2023; Patil, 2020). In the field of

geosciences, AI has been increasingly used for

natural disaster predictions. For instance,

Makinoshima et al. proposed a deep learning model

106

Cai and Y.

Evaluating the Generalizability of Machine Learning Models for Seismic Data Prediction Across Different Regions.

DOI: 10.5220/0013509700004619

In Proceedings of the 2nd International Conference on Data Analysis and Machine Learning (DAML 2024), pages 106-114

ISBN: 978-989-758-754-2

using Convolutional Neural Networks (CNNs) that

integrates geodetic observation data and

oceanographic data to predict tsunami events along

the Pacific coast of Japan (Makinoshima, 2021).

Similarly, Ruttgers et al. used Generative Adversarial

Networks (GAN) to predict the trajectory and

intensity of typhoons in the Northwest Pacific based

on historical meteorological data (Ruttgers, 2022). In

earthquake prediction, Cui et al. (2021) employed a

stacking-based ensemble learning model for

earthquake casualty prediction. The model employs

XGBoost, Bagged Decision Trees, and Gradient

Boosting Decision Trees (GBDT) as first-level base

learners and GBDT as a second-level meta-learner.

Popular machine learning techniques including SVM,

RF, and Classification and Regression Trees (CART)

were surpassed by the suggested approach (Cui,

2021). Additionally, Iaccarino et al. (2023) utilized a

Gradient Boosting Regressor (GBR) and achieved

reliable results in predicting the seismic ground

motion intensity (Iaccarino, 2023).

Despite these advances, current approaches often

fail to consider variations in geographical

distributions, such as the differences between seismic

activities in the Eastern and Western Hemispheres.

This limitation could affect the generalizability of

models when applied to regions with distinct

geological characteristics. In order to close this gap,

the present work uses seismic data from various

hemisphere distributions to assess how well various

machine learning models predict earthquake

magnitudes. By systematically comparing the

generalization capabilities of models trained on

Eastern Hemisphere data and tested on Western

Hemisphere data, the study aims to provide insights

into the robustness and adaptability of popular AI

models for seismic prediction.

The technical approach of this research involves

dividing the seismic data into two classes: Eastern

Hemisphere and Western Hemisphere. The models

under consideration include LR, SVR, RF, KNN, and

DTs. The methodology is structured as follows: (1)

preprocessing and feature extraction from the seismic

dataset, (2) training models using Eastern

Hemisphere data, (3) evaluating model performance

on Western Hemisphere data, and (4) examining and

contrasting the models' generalizability using

different assessment metrics, including Mean

Absolute Error (MAE), MSE, Root Mean Squared

Error (RMSE), and R². The study also explores the

implications of these findings for improving seismic

prediction models and enhancing their practical

applicability in disaster management.

2 METHOD

This section outlines the dataset preparation, the

specific machine learning models utilized, and the

evaluation metrics adopted in this study. The aim is

to assess the generalizability of various machine

learning models in predicting earthquake magnitudes

based on seismic data from different hemispheres (i.e.

training on Eastern Hemisphere and testing on

Western Hemisphere).

2.1 Dataset Preparation

The seismic dataset used in this study was sourced

from USGS, which provides a comprehensive

collection of earthquake data worldwide (USGS,

2024). The data covers seismic events from the

Eastern Hemisphere and the Western Hemisphere.

Specifically, the data range from records of

earthquakes with magnitudes greater than 4.5 since

2020, with 19,671 records collected in the Eastern

Hemisphere and 14,075 records in the Western

Hemisphere, providing a robust basis for model

training and testing. The dataset consists of 22

features in total such as time and latitude.

Given the scope and nature of this study, which

focuses on predicting earthquake magnitudes, the

primary target variable is "Magnitude(ergs)." The

task is thus framed as a regression problem. The

dataset underwent feature selection and index

conversion as part of preprocessing to improve model

performance and lower complexity. The "time"

feature was converted into an index to simplify

chronological ordering, while the number of features

was reduced to eight essential predictors:

"Latitude(deg)," "Longitude(deg)," "Depth(km),"

"Magnitude(ergs)," "Magnitude_type,"

"No_of_Stations," "horizontalError," and

"depthError." Notably, the dataset did not contain

missing values, obviating the need for imputation.

In this study, the models use six features for

prediction: "Latitude(deg)," "Longitude(deg),"

"Depth(km)," "No_of_Stations," "horizontalError,"

and "depthError." The training and testing datasets

are divided based on hemispheres: the Eastern

Hemisphere dataset is used for training, while the

Western Hemisphere dataset is used for testing. This

division is critical in evaluating the generalizability of

the models across different geographic distributions.

Evaluating the Generalizability of Machine Learning Models for Seismic Data Prediction Across Different Regions

107

2.2 Machine Learning Models-Basesd

Prediction

The study employs five distinct machine learning

models: LR, SVR, RF Regression, KNN Regression,

and DT Regression. All models were implemented

using the scikit-learn (sklearn) library in Python. To

verify each model's generalizability, it was first

trained using data from the Eastern Hemisphere and

then tested using data from the Western Hemisphere.

These metrics were used to assess each model's

performance: R², MAE, MSE, and RMSE.

2.2.1 Linear Regression

Regression analysis's most basic and widely applied

algorithm is LR. It explains the relationship between

a dependent variable and one or more independent

variables by fitting a linear equation to observable

data. The formula for a simple LR is given as:

𝑦=𝛽



+𝛽



𝑥+𝜖

(1)

Where 𝑦 stands for the predicted value, 𝛽



for the

intercept, 𝛽



for the slope of the line, 𝑥 for the input

variable, and 𝜖 for the error term (Maulud, 2020). By

minimizing the sum of squared residuals—the

variations between observed and anticipated values—

the least squares method was used in this study to fit

the model. More intricate models can be compared to

the LR model as a baseline.

2.2.2 Support Vector Regression

SVR extends the principles of SVM to regression

tasks. The primary objective of SVR is to find a

hyperplane that best fits the data points within a

predefined margin of tolerance (Bansal, 2022). SVR

uses a kernel trick to transform data into a higher-

dimensional space, making it easier to perform LR in

this transformed space. The Radial Basis Function

(RBF) kernel is widely used in SVR due to its

flexibility in handling non-linear data patterns. The

RBF kernel function is defined as (Montesinos,

2022):



𝑥



,𝑥





=exp



−𝛾



𝑥



−𝑥









(2)

The SVR model used in this work has the

following hyperparameters set: gamma = 0.1, C = 1,

and kernel = 'rbf'. The influence of individual data

points is defined by the parameter "gamma," while

the trade-off between obtaining a narrow error margin

and preserving a smooth decision border is managed

by the parameter "C." When there is a non-linear

relationship between characteristics, SVR is

especially helpful, which makes it a good fit for

complex seismic data.

2.2.3 Random Forest Regression

RF is an ensemble learning technique that lessens

overfitting and increases accuracy by combining the

predictions of several Decision Trees. In regression

tasks, RF averages the outputs of individual trees to

produce a final prediction. To ensure diversity across

the trees, each tree is trained on a random portion of

the data and only takes into account a random subset

of features for splitting at each node (Genuer, 2020).

The hyperparameters for the RF Regressor used in

this study were set as ‘n_estimators=1000’, where

‘n_estimators’ represents the number of Decision

Trees in the forest. The model is an effective tool for

estimating earthquake magnitudes because of its

resilience to noise and capacity to manage high-

dimensional data, particularly in situations where the

data distribution is intricate and has non-linear

correlations.

2.2.4 K-Nearest Neighbors Regression

A non-parametric, instance-based learning approach

called KNN Regression uses the values of a data

point's k-nearest neighbors to predict the value of a

new data point. The target point and every other point

in the training set are measured using the Euclidean

distance technique. The prediction is then determined

by averaging the values of the k-nearest neighbors

(Bansal, 2022).

In this study, the value of k was set to 5

(‘n_neighbors=5’), which balances bias and variance.

Even while KNN is easy to use and understand, when

working with big datasets, it can be computationally

demanding and sensitive to the size of the features.

Despite these limitations, KNN was included in this

study for its effectiveness in capturing local data

patterns and trends.

2.2.5 Decision Tree Regression

A non-linear predictive model called DT Regression

divides the dataset recursively at decision nodes until

a leaf node is reached. It does this by dividing the data

into subsets according to feature values. The final

prediction is contained in the leaf node, while each

decision node represents a feature and each branch a

potential result. The DT algorithm selects the feature

that results in the highest information gain or lowest

mean squared error at each split (Bansal, 2022).

DAML 2024 - International Conference on Data Analysis and Machine Learning

108

Although DTs are prone to overfitting, they are

easy to visualize and interpret, making them a

valuable tool for exploring feature importance and

model behavior (Charbuty, 2021). In this study, a

standard DT Regressor was employed with default

settings.

3 RESULTS AND DISCUSSION

This section presents the findings of the study and

offers a critical analysis of the results obtained from

applying five machine learning models—LR, SVR,

RF, KNN, and DT—to earthquake magnitude

prediction. In the subsequent analysis, the strengths,

weaknesses, and insights gained from the

experiments are discussed in detail, alongside a

reflection on the limitations and suggestions for

future improvements.

3.1 The Performance of Models

The results of the experiment are provided in Table 1,

where the performance metrics for each model are

summarized.

The RF model consistently outperformed the

other models in terms of predictive performance; it

had the lowest MAE (0.2331), MSE (0.1057), RMSE

(0.3251), and positive R² value (0.2230). These

measures show that when it comes to predicting

earthquake magnitudes across various geographies,

the RF model has a more favorable balance between

bias and variance, which leads to improved

generalizability. On the other hand, the KNN model

performed the worst, as evidenced by large error rates

and a markedly negative R² value (-0.6002),

indicating inadequate dataset adaption.

To better visualize the performance of each

model, scatter plots depicting actual versus predicted

values were generated for each model:

The scatter plot shown in Figure 1 reveals that the

model tends to underestimate earthquake magnitudes,

particularly for magnitudes exceeding 5. The

alignment of points close to the perfect prediction line

is mostly observed for lower magnitudes, where

linearity assumptions hold.

The SVR model shown in Figure 2 shows a highly

clustered set of predictions with limited variance,

indicating that the model struggles to capture the

dynamic range of the data. This results in consistently

inaccurate predictions.

The scatter plot shown in Figure 3 shows the RF

model’s predictions are closely aligned with actual

values, with most prediction errors within a 1 to 1.5

unit range. This suggests that the ensemble approach

effectively captures complex relationships.

The KNN’s in Figure 4 predictions are

concentrated between 4.5 and 5.5, leading to

significant inaccuracies for larger earthquake

magnitudes. The pattern highlights the model’s

inability to generalize beyond local data points.

The DT model shown in Figure 5 demonstrates

considerable prediction errors, with points scattered

away from the perfect prediction line, particularly in

the lower left corner. This reflects the model’s

tendency toward high variance and overfitting.

Additionally, two key plots provide further

insights:

A feature importance plot shown in Figure 6 for

the RF model highlights the relative importance of

each input feature. Notably, the features "No. of

Stations" and "Depth Error" stand out as the most

influential factors in predicting earthquake

magnitudes.

A line plot shown in Figure 7 showing the first

100 actual and predicted values in the test dataset for

the RF model illustrates that while the model follows

the general trend, there are noticeable deviations,

particularly at higher magnitudes. This indicates

some limitations in fully capturing the non-linear

relationships in seismic data.

Table 1: Performance Metrics of Each Model.

Model Name

MAE MSE RMSE R²

Linear Re

ression 0.241816 0.131785 0.363022 0.031435

SVR 0.277640 0.137359 0.370620 -0.009529

Rando

Fores

0.233067 0.105717 0.325141 0.223026

KNN 0.373962 0.217721 0.466606 -0.600158

Decision Tree 0.302034 0.199197 0.446315 -0.464016

Evaluating the Generalizability of Machine Learning Models for Seismic Data Prediction Across Different Regions

109

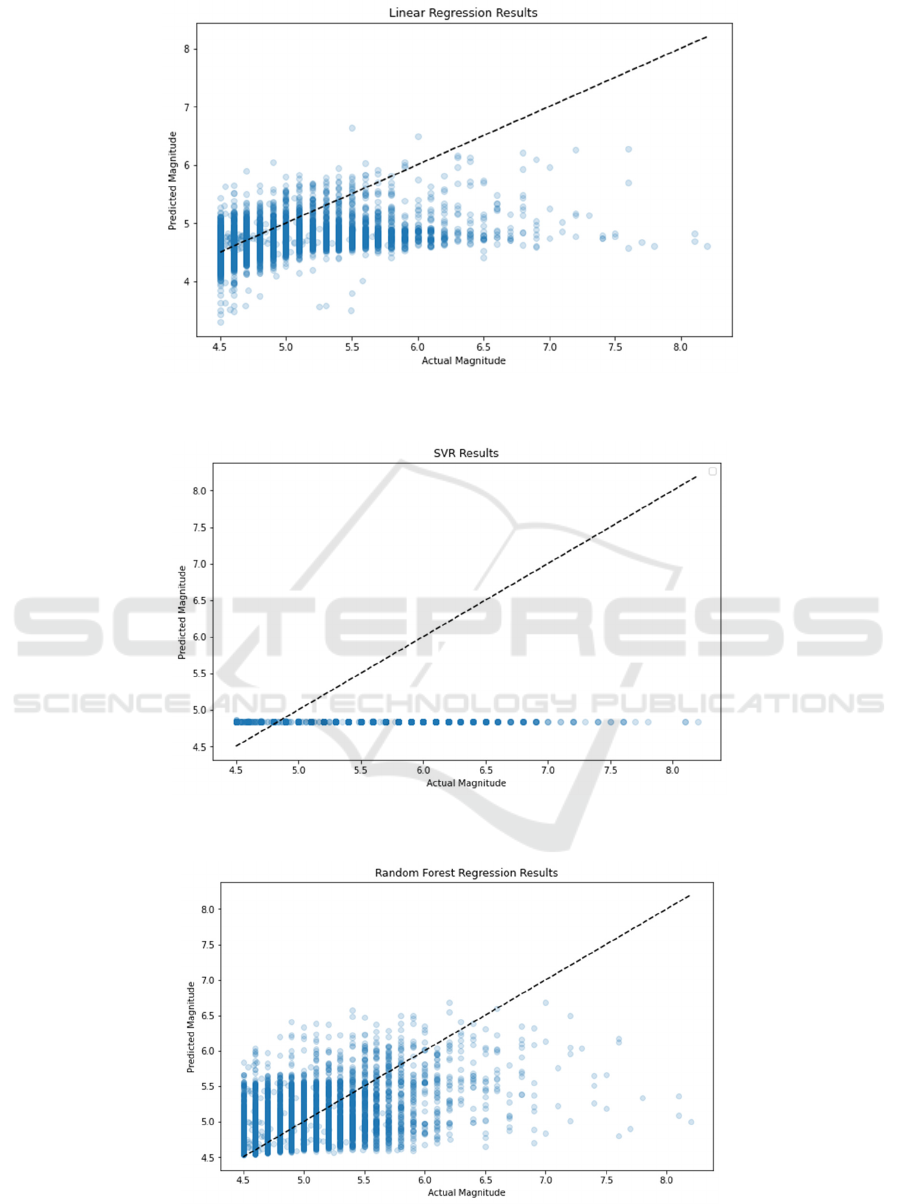
Figure 1: Linear Regression Result (Photo/Picture credit: Original).

Figure 2: SVR Result (Photo/Picture credit: Original).

Figure 3: Random Forest Result (Photo/Picture credit: Original).

DAML 2024 - International Conference on Data Analysis and Machine Learning

110

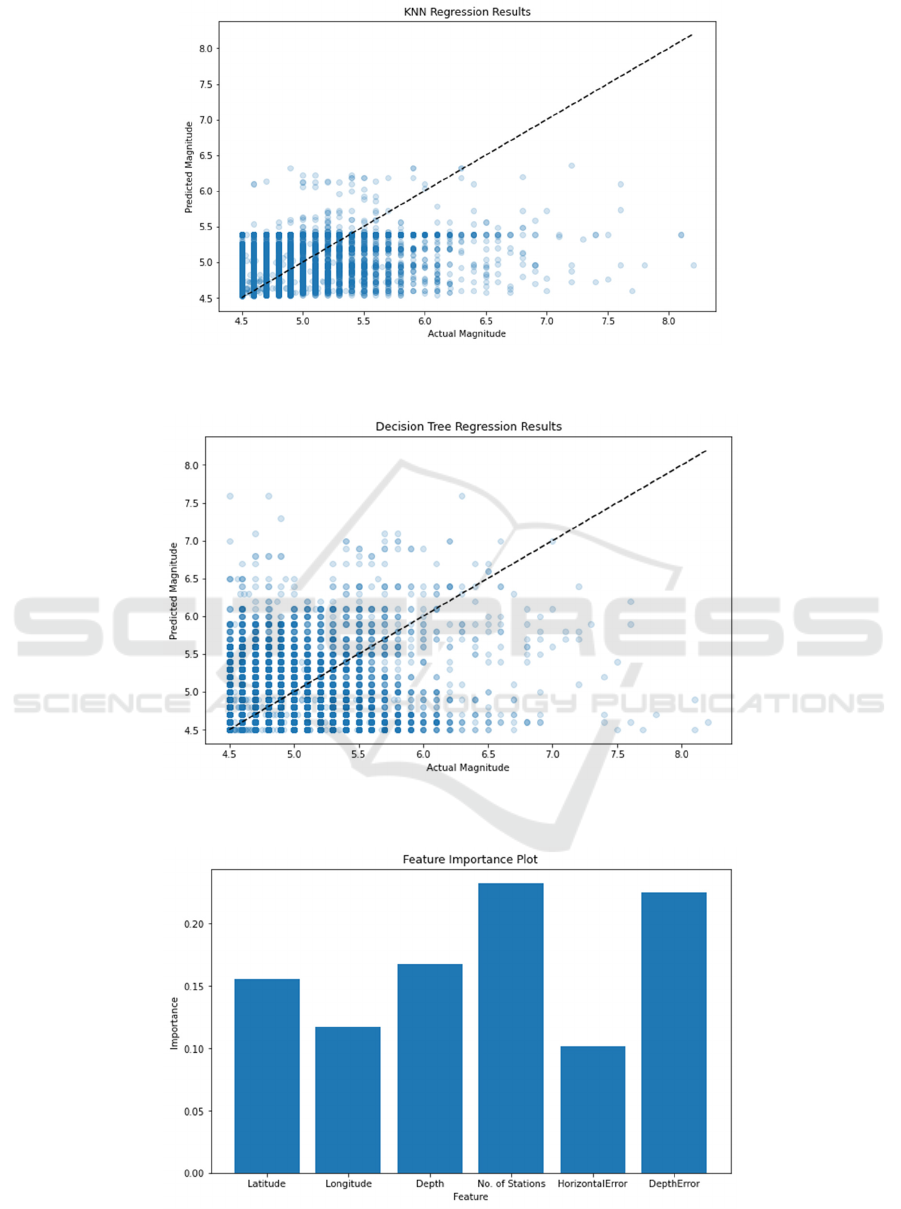
Figure 4: KNN Result (Photo/Picture credit: Original).

Figure 5: Decision Tree Result (Photo/Picture credit: Original).

Figure 6: Feature Importance Plot (Photo/Picture credit: Original).

Evaluating the Generalizability of Machine Learning Models for Seismic Data Prediction Across Different Regions

111

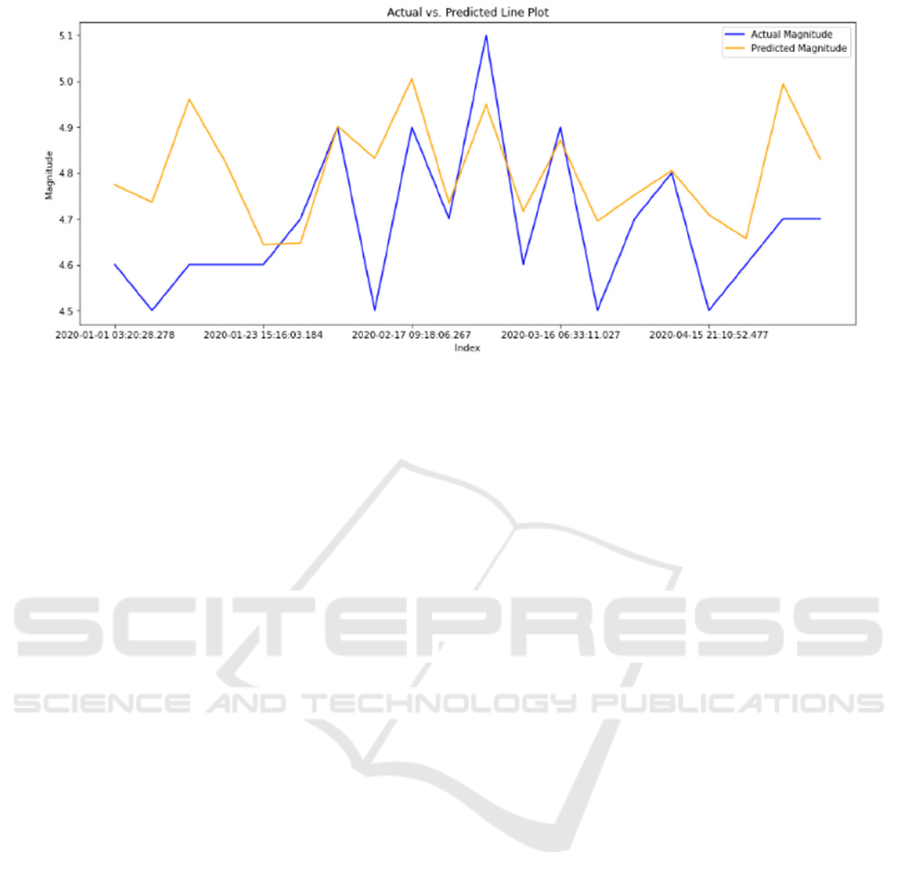
Figure 7: Actual vs. Predicted Line Plot (Photo/Picture credit: Original

3.2 Analysis and Discussion

The study's conclusions offer significant new

understandings into the applicability of different

machine learning methods for assessing the size of

earthquakes in diverse geographic locations. The

ensemble aspect of the RF model, which combines

several Decision Trees to average out mistakes and

lower the risk of overfitting, is responsible for its

better performance. For a complicated task like

earthquake prediction, this method is very useful in

capturing non-linear correlations and interactions

among the characteristics. Large feature spaces and

reduced variance were advantages of the RF model in

this investigation, which led to more accurate

predictions.

In contrast, the KNN model’s poor performance is

largely due to its sensitivity to noisy data and its

reliance on localized patterns. The model tends to

perform well when data is uniformly distributed;

however, in this case, the geographic and

seismological variations across different regions

introduce significant challenges. The high-

dimensional feature space further exacerbates the

model’s limitations, leading to suboptimal

predictions clustered within a narrow range.

The LR model, while simple and interpretable,

failed to capture the complex relationships inherent in

the data. The model works well for linear trends, as

seen in its reasonably good predictions for

magnitudes below 5, but struggles with non-linear

patterns, leading to consistent underestimations for

higher magnitudes.

The SVR model, using an RBF kernel, did better

at capturing some non-linearities, but its performance

was hindered by the challenge of tuning

hyperparameters like the penalty parameter (C) and

kernel coefficient (γ). The model’s tendency to

produce similar predictions regardless of input

variations suggests it did not generalize well to the

unseen test set.

The DT model, despite being interpretable and

fast, showed high variance, leading to overfitting. The

model’s lack of regularization resulted in large

prediction errors, as seen in the widely scattered

points on the scatter plot. This behavior is typical of

DTs when they fail to generalize beyond the training

data.

Several important findings emerge from this

study. First, models trained solely on Eastern

Hemisphere data struggled to generalize effectively

to Western Hemisphere data, emphasizing the

importance of considering regional heterogeneity in

seismic modeling. This result points to a potential

limitation in some existing predictive models that are

typically trained on data from one geographic area. It

also underscores the necessity of employing transfer

learning techniques or training region-specific

models when dealing with the task of global

earthquake prediction.

Second, the study emphasizes how crucial feature

selection is and how it affects model performance.

The RF’s ability to identify the importance of features

like "No. of Stations" and "Depth Error" provides

valuable guidance for future research, suggesting that

integrating additional features related to seismic

activity, geological composition, and real-time

monitoring could further enhance prediction

accuracy.

DAML 2024 - International Conference on Data Analysis and Machine Learning

112

4 CONCLUSIONS

This paper investigates the generalizability of five

machine learning models—LR, SVR, RF, KNN, and

DT—in predicting earthquake magnitudes across

different geographical distributions. By using seismic

data from the Eastern Hemisphere for training and

testing on data from the Western Hemisphere, the

study highlights the varying effectiveness of these

models in handling data distribution shifts. Among

the models, RF demonstrated the best predictive

performance, while KNN showed the least accuracy.

The experimental results underscore the importance

of model selection when dealing with datasets from

different regions.

The study's conclusions advance the knowledge

of model migration and adaptability, particularly in

applying machine learning models to datasets with

diverse distributions. This exploration is crucial for

improving the robustness of predictive models in

seismology, potentially aiding in better disaster

preparedness and risk mitigation.

However, the study is not without limitations,

such as the exclusion of more granular regional data

and the lack of temporal dynamics consideration.

Future work should address these limitations by

incorporating localized geophysical factors and

evolving seismic patterns to enhance model

generalization further.

REFERENCES

Aguilar, D. L., Medina-Pérez, M. A., Loyola-González, O.,

Choo, K.-K. R., & Bucheli-Susarrey, E. 2023. Towards

an interpretable autoencoder: A decision-tree-based

Autoencoder and its application in anomaly detection.

IEEE Transactions on Dependable and Secure

Computing, 20(2), 1048–1059.

https://doi.org/10.1109/tdsc.2022.3148331

Banna, Md. H., Taher, K. A., Kaiser, M. S., Mahmud, M.,

Rahman, Md. S., Hosen, A. S., & Cho, G. H. 2020.

Application of artificial intelligence in predicting

earthquakes: State-of-the-art and future challenges.

IEEE Access, 8, 192880–192923.

https://doi.org/10.1109/access.2020.3029859

Bhatia, M., Ahanger, T. A., & Manocha, A. 2023. Artificial

intelligence based real-time earthquake prediction.

Engineering Applications of Artificial Intelligence,

120, 105856.

https://doi.org/10.1016/j.engappai.2023.105856

Cui, S., Yin, Y., Wang, D., Li, Z., & Wang, Y. 2021. A

stacking-based ensemble learning method for

earthquake casualty prediction. Applied Soft

Computing, 101, 107038.

https://doi.org/10.1016/j.asoc.2020.107038

Duan, Y., Di, B., Ustin, S. L., Xu, C., Xie, Q., Wu, S., Li,

J., & Zhang, R. 2021. Changes in ecosystem services in

a montane landscape impacted by major earthquakes: A

case study in wenchuan earthquake-affected area,

China. Ecological Indicators, 126, 107683.

https://doi.org/10.1016/j.ecolind.2021.107683

Goodell, J. W., Kumar, S., Lim, W. M., & Pattnaik, D.

2021. Artificial Intelligence and machine learning in

finance: Identifying foundations, themes, and research

clusters from Bibliometric analysis. Journal of

Behavioral and Experimental Finance, 32, 100577.

https://doi.org/10.1016/j.jbef.2021.100577

Iaccarino, A. G., Cristofaro, A., Picozzi, M., Spallarossa,

D., & Scafidi, D. 2023. Real-time prediction of distance

and PGA from p-wave features using gradient boosting

regressor for on-site earthquake early warning

applications. Geophysical Journal International,

236(1), 675–687. https://doi.org/10.1093/gji/ggad443

Makinoshima, F., Oishi, Y., Yamazaki, T., Furumura, T., &

Imamura, F. 2021. Early forecasting of tsunami

inundation from Tsunami and geodetic observation data

with convolutional neural networks. Nature

Communications, 12(1).

https://doi.org/10.1038/s41467-021-22348-0

Mavrouli, M., Mavroulis, S., Lekkas, E., & Tsakris, A.

2023. The impact of earthquakes on Public Health: A

Narrative Review of Infectious Diseases in the post-

disaster period aiming to disaster risk reduction.

Microorganisms, 11(2), 419.

https://doi.org/10.3390/microorganisms11020419

Mignan, A., & Broccardo, M. 2020. Neural network

applications in earthquake prediction (1994–2019):

Meta-analytic and statistical insights on their

limitations. Seismological Research Letters, 91(4),

2330–2342. https://doi.org/10.1785/0220200021

Patil, A., & Rane, M. 2020. Convolutional Neural

Networks: An overview and its applications in pattern

recognition. Smart Innovation, Systems and

Technologies, 21–30. https://doi.org/10.1007/978-981-

15-7078-0_3

Pisner, D. A., & Schnyer, D. M. 2020. Support Vector

Machine. Machine Learning, 101–121.

https://doi.org/10.1016/b978-0-12-815739-8.00006-7

Ruttgers, M., Jeon, S., Lee, S., & You, D. 2022. Prediction

of typhoon track and intensity using a generative

adversarial network with observational and

Meteorological Data. IEEE Access, 10, 48434–48446.

https://doi.org/10.1109/access.2022.3172301

Secinaro, S., Calandra, D., Secinaro, A., Muthurangu, V.,

& Biancone, P. 2021. The role of Artificial Intelligence

in healthcare: A structured literature review. BMC

Medical Informatics and Decision Making, 21(1).

https://doi.org/10.1186/s12911-021-01488-9

Sun, W., Bocchini, P., & Davison, B. D. 2020. Applications

of artificial intelligence for disaster management.

Natural Hazards, 103(3), 2631–2689.

https://doi.org/10.1007/s11069-020-04124-3

Ullo, S. L., & Sinha, G. R. 2020. Advances in smart

environment monitoring systems using IOT and

Evaluating the Generalizability of Machine Learning Models for Seismic Data Prediction Across Different Regions

113

sensors. Sensors, 20(11), 3113.

https://doi.org/10.3390/s20113113

Wald, D. J. 2020. Practical limitations of earthquake early

warning. Earthquake Spectra, 36(3), 1412–1447.

https://doi.org/10.1177/8755293020911388

DAML 2024 - International Conference on Data Analysis and Machine Learning

114