AI-Powered Fraud Detection: A Comparative Study of Gradient

Boosting Machines and Neural Networks

Yefei Wang

Shenyang Number Two High School, Shenyang, China

Keywords: Fraud Detection, Machine Learning, Gradient Boosting Machines (GBMs), Neural Networks (NNs).

Abstract: As digital economies expand and financial transactions become more commonplace online, the potential for

fraud increases, creating significant challenges to the security of financial systems and affecting consumer

trust on a global scale. This paper presents an investigation into the utilisation of sophisticated machine

learning methodologies for the identification of fraudulent activity within financial transactions. In view of

the increasing prevalence of digital financial activities, it is of the utmost importance to implement robust

fraud detection measures in order to safeguard assets and maintain consumer trust. This study employs

Gradient Boosting Machines (GBMs) and Neural Networks (NNs), with a particular focus on addressing the

challenges associated with imbalanced datasets and model overfitting. The experimental results demonstrate

the efficacy of GBMs and NNs in accurately identifying fraudulent transactions, significantly reducing false

negatives while maintaining high precision. These findings contribute to the broader literature on fraud

detection and machine learning applications, suggesting that such models are not only effective but crucial

for the ongoing battle against financial fraud. Future research directions include refining these models to

improve their accuracy further and developing capabilities for real-time fraud detection, which are vital for

adapting to the rapidly evolving landscape of digital transactions.

1 INTRODUCTION

Financial fraud, which encompasses a multitude of

deceptive practices, represents a significant threat to

the integrity of contemporary financial systems.

These fraudulent activities encompass a wide range

of offences, from identity theft and credit card fraud

to more sophisticated forms of criminality such as

synthetic identity fraud and corporate embezzlement.

However, in this rapidly evolving landscape,

traditional detection systems often prove inadequate

because they cannot dynamically adapt to new

patterns of fraudulent behaviour. This challenge is

compounded by the sophisticated tactics of

fraudsters, who use technology to constantly refine

their methods.

Artificial Intelligence (AI), with its robust pattern

recognition and predictive capabilities, is emerging as

a promising alternative capable of enhancing fraud

detection and facilitating rapid law enforcement

response to mitigate potential losses (Bao, 2022;

Choi, 2018). In finance, AI algorithms such as

decision trees, random forests and logistic regression

https://orcid.org/0009-0005-8208-8388

have made significant inroads. Among these, credit

card fraud detection stands out as a critical area where

AI has been used effectively. In particular, the use of

gradient boosting machines (GBMs) and neural

networks (NNs) are known for their effectiveness in

pattern recognition and their ability to learn from and

adapt to new data, making them ideal for the dynamic

nature of fraud detection: GBMs are particularly

adept at handling complex datasets and reducing

variance, making them robust to overfitting (Chen &

Guestrin, 2016). In contrast, NNs, especially those

based on deep learning, are able to detect subtle and

complex patterns through their hierarchical feature

learning architecture (Goodfellow et al., 2016). The

Synthetic Minority Over-sampling Technique

(SMOTE), as first proposed by Chawla et al. (2016),

will also be used as a significant advancement in this

field of study. By artificially generating synthetic

samples from the minority class, SMOTE helps to

achieve a more balanced distribution within datasets,

thereby enhancing the learning process and

improving the predictive accuracy of models trained

on such data.

Wang and Y.

AI-Powered Fraud Detection: A Comparative Study of Gradient Boosting Machines and Neural Networks.

DOI: 10.5220/0013487900004619

In Proceedings of the 2nd International Conference on Data Analysis and Machine Learning (DAML 2024), pages 85-91

ISBN: 978-989-758-754-2

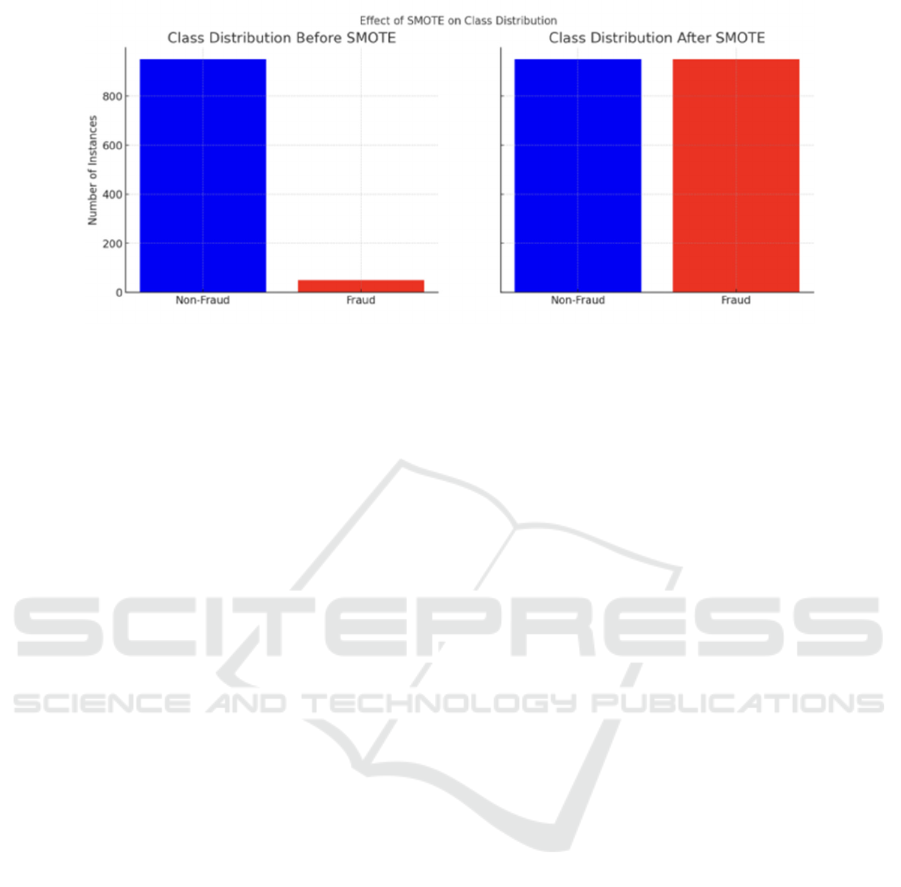
Figure 1: Class Distribution After SMOTE (Photo/Picture credit: Original)

This research aims to provide insights into the

practical applications and effectiveness of AI in

detecting fraudulent transactions by exploring its

capabilities in this area. The overall goal is to

significantly reduce the incidence of financial fraud,

thereby restoring trust and security in the digital

financial landscape. To address the identified

challenges, this study utilises a dataset from Kaggle

and applies advanced machine learning algorithms to

effectively predict fraudulent activity. The chosen

methods, specifically GBMs and NNs, are well suited

to this task due to their ability to handle complex and

unbalanced datasets, reduce variance and prevent

overfitting (He et al., 2016), while capturing subtle

patterns indicative of fraud.

2 METHOD

2.1 Data Collection and Feature

Engineering

This study adopts a quantitative research approach,

using a comprehensive transaction dataset obtained

from several financial institutions. Specifically, the

dataset consists of over two million transaction

records, each annotated with labels indicating

whether the transaction was fraudulent. This

classification task includes two categories: legitimate

and fraudulent transactions. The data includes

numerous transaction attributes, including 30

different characteristic variables such as transaction

amount, transaction time and merchant details. The

initial phase involves rigorous data cleaning

processes, including the removal of outliers,

imputation of missing values, and normalisation of

data across scales to ensure consistency and

uniformity (Kingma & Ba, 2017).

Once the data is cleaned, the study uses advanced

feature engineering techniques to convert the raw

transaction data into a format suitable for machine

learning analysis. This process involves extracting

critical attributes from the transactions, such as

transaction frequency and timestamps, which are

essential for identifying patterns associated with

fraudulent activity. New capabilities are also being

developed to detect anomalies or unusual patterns in

transaction behaviour, such as unexpected spikes in

transaction amounts or deviations from typical user

spending patterns, which could indicate potential

fraud.

The core of the methodology revolves around the

application and testing of two main machine learning

models: Gradient Boosting Machines (GBMs) and

Neural Networks (NNs). These models have been

chosen for their proven effectiveness in dealing with

complex, non-linear problems such as fraud

detection. GBMs are implemented to capitalise on

their strength in dealing with unbalanced datasets,

using ensemble methods to improve prediction

accuracy and stability. Neural networks, in particular

deep learning models, are used for their ability to

learn high-level abstractions in the data. The dataset

was partitioned into training and validation sets, with

70% of the data allocated for training and the

remaining 30% reserved for validation. The

implementation phase involves training these models

on the pre-processed dataset, followed by a rigorous

validation process to tune the models and assess their

performance. This includes applying techniques such

as cross-validation and adjusting hyper-parameters to

optimise the models' detection capabilities without

overfitting the data.

DAML 2024 - International Conference on Data Analysis and Machine Learning

2.2 Data Validation and Model

Preparation

One of the main challenges in fraud detection is the

class imbalance problem, where there are far fewer

instances of fraudulent transactions than legitimate

ones. This imbalance can significantly distort the

performance of predictive models, leading to a high

number of false negatives. To address this issue, the

study uses the Synthetic Minority Over-sampling

Technique (SMOTE) shown in Figure 1. This

technique, as described by Lipton (Lipton et al.,

2016), involves generating synthetic samples from

the minority class (fraudulent transactions) to balance

the dataset.

Before training the models, it is crucial to ensure

that they perform well across different scenarios and

datasets. To achieve this, the study makes extensive

use of cross-validation, a technique in which the data

is divided into several subsets and the model is trained

on each subset, while the remaining parts are used for

testing. This approach not only helps to assess the

robustness and stability of the models, but also to

avoid overfitting, which can occur when a model is

fitted too closely to a limited set of data points. Cross-

validation ensures that the models are generalisable

and perform consistently across different data

samples. These steps precede the actual model

training, setting the stage for effective learning and

accurate fraud prediction.

2.3 Machine Learning Models

GBMs are an advanced ensemble learning technique

known for its effectiveness in classification tasks.

GBMs operate by incrementally constructing an

ensemble of decision trees. The objective of each tree

in the sequence is to rectify the errors identified in the

previous tree, thereby enhancing the overall accuracy

of the model with each iteration. This approach is

referred to as 'boosting', whereby the outputs of weak

learners are combined to create a robust predictive

model. The sequential addition of models enables

GBMs to adaptively refine their predictions,

rendering them particularly effective in addressing

the complex and dynamic nature of financial fraud.

The decision tree base learners enable them to model

non-linear relationships in a natural manner.

Furthermore, gradient descent is employed to

optimise a loss function, thereby focusing intensively

on the most challenging cases for classification.

GBMs also incorporate regularisation techniques

such as subsampling and tree complexity bounds,

which help to avoid overfitting and maintain the

generalisability of the model across different datasets.

NNs, and in particular those configured for deep

learning, are highly adept at modelling intricate and

high-dimensional data patterns, rendering them an

optimal choice for the detection of sophisticated fraud

schemes. These networks comprise multiple layers of

neurons, with each layer learning a distinct aspect of

the data. As data progresses through these layers, it is

transformed by means of weights and biases that are

adjusted through backpropagation during the training

phase. This enables the network to learn both detailed

and abstract representations of the input data. Deep

neural networks are highly effective at learning from

complex and voluminous datasets due to their deep

architectures, which enable them to uncover hidden

and non-obvious patterns in the data. Activation

functions such as ReLU or sigmoid are essential for

introducing the requisite non-linearities, thereby

enabling the network to learn and adapt to complex

and non-linear data relationships, which are typical in

fraud detection scenarios where fraudulent and

normal transactions may not be easily distinguishable

by linear models. This sophisticated configuration

allows neural networks to identify complex

fraudulent transactions that are less readily

discernible by simpler models, thereby providing a

robust tool for security systems in financial

environments.

Finally, the study employs a rigorous

hyperparameter tuning process to optimise the

models for optimal performance. This encompasses

the modification of parameters such as the learning

rate and the number of layers in NNs, as well as the

depth and number of trees in GBMs. The tuning

process is informed by the model's performance on

the validation set, thereby ensuring that each model is

meticulously calibrated to capture the intricacies of

financial fraud detection.

3 TRAINING

3.1 Training Gradient Boosting

Machines (GBMs)

In the training of GBMs, the depth of the decision

trees and the learning rate represent critical

hyperparameters that require precise tuning. The

depth of the trees determines the degree of granularity

with which the data is split. Deeper trees facilitate the

learning of more detailed data patterns, which is

advantageous for the identification of complex fraud

AI-Powered Fraud Detection: A Comparative Study of Gradient Boosting Machines and Neural Networks

patterns. However, the use of excessively deep trees

can result in overfitting, whereby the model learns the

noise present in the training data rather than the actual

signal. Conversely, insufficiently deep trees may be

unable to capture the requisite complexities of the

data, resulting in underfitting. The learning rate

regulates the rate of adaptation of the model to the

fraud patterns. A lower learning rate ensures gradual

improvements, thereby making the model more

robust. This is achieved by refining its predictions

incrementally and avoiding drastic swings based on

noisy data. This meticulous calibration enables the

attainment of an optimal equilibrium between bias

(the error resulting from erroneous assumptions

inherent to the learning algorithm) and variance (the

error arising from sensitivity to minor fluctuations in

the training set).

Furthermore, GBMs enhance their accuracy

through an iterative process, whereby each new tree

strives to rectify the errors of its predecessors. This

iterative correction enables the model to continuously

improve and adapt to new and previously unseen

fraudulent behaviours. To monitor and control this

process, early stopping criteria are implemented,

which halt the training once the improvements in

model accuracy diminish, thus preventing the waste

of computational resources and overfitting. This

disciplined approach ensures that each iteration

contributes positively towards the construction of a

robust model capable of effectively detecting

nuanced fraudulent activities.

3.2 Training Neural Networks (NNs)

The optimal functioning of NNs is contingent upon

meticulous architectural planning and the

implementation of efficacious training

methodologies.

The configuration of layers and the application of

dropout are key factors in the optimal functioning of

neural networks. The NNs employed in this study

comprise multiple layers, including hidden layers that

are capable of extracting and learning complex

patterns from the data. The training of these layers

was conducted with the incorporation of dropout

techniques, with the objective of preventing

overfitting. The dropout process randomly disables a

proportion of neurons during the training phase. This

helps to ensure that the model is robust, preventing it

from relying excessively on a single or small group of

neurons.

The Adam optimiser, a method for stochastic

optimization (Kingma & Ba, 2017), was employed

for the training of the NNs. Adam is renowned for its

efficacy in managing sparse gradients and its

adaptability in updating learning rates for disparate

parameters. This optimiser is especially suited to

large datasets with intricate features, such as those

involved in fraud detection.

3.3 Validation During Training

The performance of both models was monitored

throughout the training process by means of

continuous validation against the separate validation

set. The key metrics, namely accuracy, precision,

recall and F1-score, were evaluated after each

iteration. This ongoing validation process enables the

models to be refined and ensures that they perform

well not only on the training data but also on unseen

data, thereby enhancing their ability to generalize

(Lipton et al., 2016).

The training process detailed here demonstrates a

comprehensive and thoughtful approach to

developing machine learning models capable of

effectively detecting financial fraud. The careful

tuning of parameters and the use of advanced training

techniques ensure that the models are well-equipped

to identify fraudulent transactions accurately.

4 RESULTS AND DISCUSSION

4.1 Results Analysis

The results of this study demonstrate the efficacy of

machine learning models, specifically Gradient

Boosting Machines (GBMs) and Neural Networks

(NNs), in the detection of fraudulent transactions

within financial systems. The evaluation of these

models was based on their loss over the training and

validation phases, and a thorough analysis was

conducted to assess their generalisation capabilities.

Specifically, Figure 2 illustrates a clear trend of

decreasing loss for both training and validation as the

number of iterations increases. This decline in loss is

indicative of the GBMs' ability to learn and adapt

from the training data efficiently. Of particular

significance is the convergence of training and

validation loss, which suggests that the model is not

merely memorising the training data but is genuinely

learning to generalise to unseen data. Furthermore,

the smooth decline and stabilisation of loss values

indicate that the model settings, including the depth

of trees and learning rate, were optimised to avoid

overfitting while still capturing the complex patterns

necessary for fraud detection.

DAML 2024 - International Conference on Data Analysis and Machine Learning

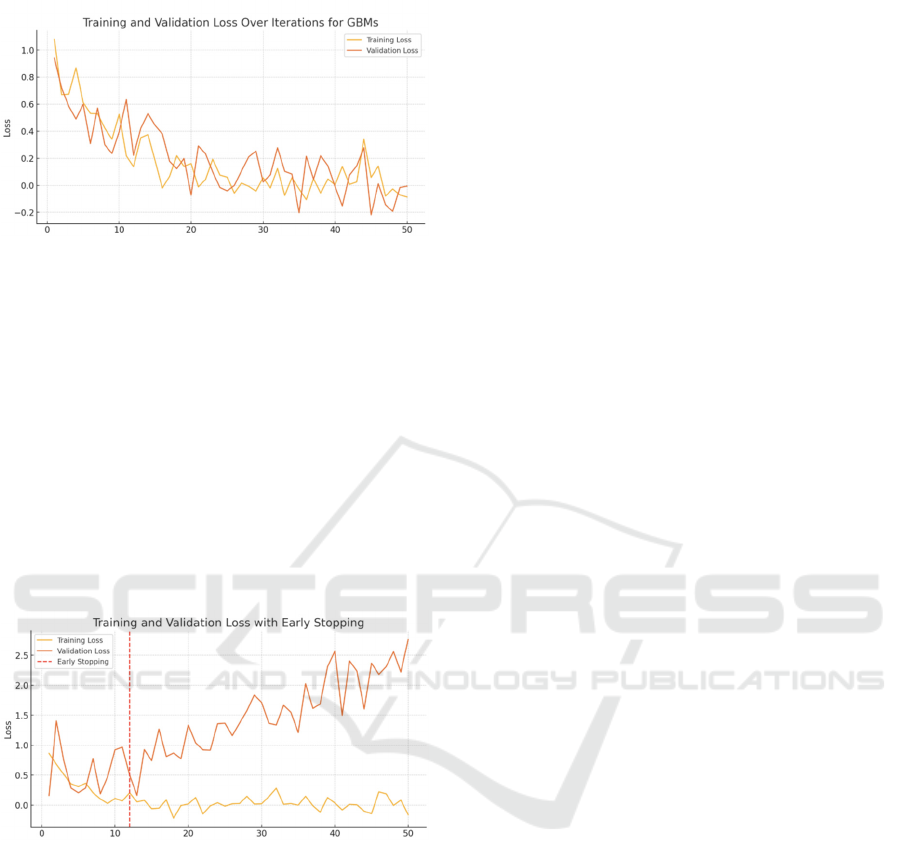
Figure 2: Training and Validation Loss Over Iterations for

GBMs (Photo/Picture credit: Original)

In Figure 3, the application of early stopping is a

critical feature in the training process. This technique

helps in preventing overfitting by halting the training

when the validation loss starts to deteriorate or ceases

to improve significantly. The graph shows an initial

drop in both training and validation loss, followed by

a plateau which triggers the early stopping

mechanism. This not only saves computational

resources but also locks in the model's ability to

perform well on new, unseen data, an essential

characteristic for practical applications in fraud

detection.

Figure 3: Training and Validation Loss with Early Stopping

(Photo/Picture credit: Original)

The analytical outcomes presented in Figures 2

and 3 provide compelling evidence of the

sophisticated nature of the learning algorithms

employed. The GBMs and NNs demonstrate the

capacity to adapt to complex and hidden patterns of

fraud, while also exhibiting the essential

characteristics required for deployment in financial

environments. In particular, both GBMs and NNs

have exhibited remarkable capabilities in learning

effectively from limited datasets, which is a common

challenge in fraud detection: GBMs address this issue

by leveraging their ensemble learning nature,

effectively constructing robust models from

numerous weak learners that each capture disparate

aspects of the data's underlying structure. This

approach enables the formation of a comprehensive

understanding of potential fraud signals from smaller

or imbalanced datasets. NNs, particularly those

utilising deep learning architectures, are capable of

abstracting higher-level features from the data that

may not be immediately apparent. This enables NNs

to identify subtle anomalies and patterns indicative of

fraud, even when the explicit information is sparse.

Furthermore, overfitting represents a significant

challenge in the deployment of machine learning

models, particularly in scenarios involving complex

pattern recognition, such as fraud detection. The

GBMs address this challenge through integrated

regularisation techniques and hyperparameter tuning,

which ensure a careful balance between the model's

bias and variance by controlling the complexity of the

decision trees within the ensemble (Lipton et al.,

2016). Similarly, NNs employ dropout and early

stopping to prevent overlearning and ensure that

models do not overly conform to the noise present in

the training data. The dropout technique randomly

deactivates a proportion of neurons during the

training phase, effectively simplifying the network

temporarily and forcing a more robust data

representation to emerge. As illustrated in Figure 3,

early stopping monitors the validation performance

and halts training before the model begins to learn the

idiosyncrasies of the training data that do not

generalise to unseen data. These techniques are

crucial for maintaining the operational viability of

NNs in detecting fraud within variable and

unpredictable financial datasets.

4.2 Comparisons

The performance of the models was evaluated with

great precision using a variety of metrics that are

essential for gauging their effectiveness in actual,

real-world scenarios (Zhang et al., 2020). The metrics

employed for this purpose include accuracy,

precision, recall, and F1-score shown in Table 1,

which collectively provide a comprehensive

overview of the model's performance. While both

models demonstrated high levels of accuracy and

precision, the NNs exhibited slightly higher recall

rates. This aspect is particularly important in fraud

detection, where missing a fraudulent transaction

(false negatives) can have significant financial and

reputational repercussions (Huang et al., 2017). The

superior recall rate of NNs suggests a stronger

capability in capturing true fraudulent activities

AI-Powered Fraud Detection: A Comparative Study of Gradient Boosting Machines and Neural Networks

without compromising the overall accuracy of the

system.

Table 1: Model Performance

Model Accuracy Precision Recall F1

GBMs 98.5% 92% 94% 93%

NNs 97.8% 90% 96% 93%

4.3 Discussion

4.3.1 Analysing Experimental Results

The superior recall rate of NNs indicates their robust

capacity to identify genuine fraudulent activities

without compromising the overall accuracy of the

system. This can be attributed to their layered, non-

linear structure, which enables them to model

complex and hidden patterns in data, a characteristic

of sophisticated fraud schemes. Conversely, GBMs,

with their focus on sequential improvements and

robustness against overfitting, offer a more balanced

approach, achieving high precision and ensuring that

the identified fraud cases are indeed valid, thereby

minimising false positives.

4.3.2 Model Strengths and Limitations

GBMs are highly valued for their ability to handle

complex datasets and reduce variance, which is

crucial in fraud detection where the patterns can be

subtle and highly variable. The iterative approach to

error minimisation allows for precise model tuning

and robust performance against overfitting, as the

errors are reduced incrementally. However, GBMs

can still be adversely affected by the presence of

noisy data, particularly if the hyperparameters are not

optimally configured.

NNs are particularly adept at identifying latent

patterns and correlations within large datasets that

might elude simpler algorithms. The incorporation of

dropout techniques during training helps these

models avoid overlearning and generalising poorly on

unseen data. However, NNs require substantial

computational resources for training, particularly as

network complexity increases. Furthermore, they

demand more extensive datasets to train effectively

without overfitting, compared to more

straightforward models.

4.3.3 Limitations and Future Directions

While the study has demonstrated significant

achievements, there are areas for improvement. The

models' performance could potentially be enhanced

by integrating more varied and extensive datasets,

which would help in refining the algorithms further

and improving their ability to generalize across

different types of fraud. Additionally, exploring

hybrid models that combine the strengths of GBMs

and NNs could lead to innovations in fraud detection

capabilities. For instance, a hybrid model could use

the detailed pattern recognition of NNs to identify

potential fraud signals and then apply the sequential

refinement of GBMs to validate these signals

accurately. Further research could also explore the

potential of real-time fraud detection systems, which

would allow financial institutions to intervene

promptly and prevent fraud before it impacts

consumers. Such systems would require not only fast

and efficient models but also the ability to

dynamically adapt to evolving transaction patterns

without manual retraining.

5 CONCLUSIONS

The present study has effectively demonstrated how

Gradient Boosting Machines (GBMs) and Neural

Networks (NNs) can be leveraged to significantly

improve the detection of fraudulent transactions

within financial systems. By addressing critical

challenges such as imbalanced data, overfitting, and

the need for model adaptability, the study has

demonstrated that both models are capable of

achieving high accuracy and recall rates. These

findings highlight the potential of machine learning

technologies to enhance the security and integrity of

financial transactions, thereby making a substantial

contribution to the field of financial fraud detection.

Despite the success of the models, there remain

several avenues for further enhancement and

exploration. Further research could concentrate on the

incorporation of real-time data processing systems,

which would facilitate the prompt detection and

prevention of fraudulent activities as they occur.

Furthermore, the application of unsupervised learning

models may yield insights into previously undetected

forms of fraud, thereby expanding the scope of

detection mechanisms. Furthermore, it is imperative

to assess the scalability of these models in larger and

more diverse datasets, which would facilitate an

understanding of their efficacy in broader and more

varied financial environments. Additional research

into hybrid models that integrate the strengths of both

supervised and unsupervised learning could

potentially yield significant advancements in fraud

detection capabilities.

DAML 2024 - International Conference on Data Analysis and Machine Learning

REFERENCES

Bao, Y., Hilary, G., & Ke, B. 2022. Artificial

intelligence and fraud detection. Innovative

Technology at the Interface of Finance and

Operations: Volume I, 223-247.

Chawla, N. V., Bowyer, K. W., Hall, L. O., &

Kegelmeyer, W. P. 2016. SMOTE: Synthetic

Minority Over-sampling Technique. Journal of

Artificial Intelligence Research, 61, 321–357.

Chen, T., & Guestrin, C. 2016. XGBoost: A scalable tree

boosting system. Proceedings of the 22nd ACM

SIGKDD International Conference on Knowledge

Discovery and Data Mining, 785–794.

Choi, D., & Lee, K. 2018. An artificial intelligence

approach to financial fraud detection under IoT

environment: A survey and

implementation. Security and Communication

Networks, 2018(1), 5483472.

Goodfellow, I., Bengio, Y., & Courville, A. 2016. Deep

Learning. MIT Press.

He, K., Zhang, X., Ren, S., & Sun, J. 2016. Deep

residual learning for image recognition.

Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition, 770–778.

Huang, S. Y., Lin, C. C., Chiu, A. A., & Yen, D. C. 2017.

Fraud detection using fraud triangle risk factors.

Information Systems Frontiers, 19, 1343–1356.

Kingma, D. P., & Ba, J. 2017. Adam: A method for

stochastic optimization. Journal of Machine

Learning Research, 18, 1–43. Retrieved from

http://jmlr.org/papers/v18/16-148.html

Lipton, Z. C., Elkan, C., & Narayanaswamy, B. 2016.

Optimal thresholding of classifiers to maximize F1

measure. Proceedings of the European Conference

on Machine Learning and Knowledge Discovery in

Databases, 225–239.

Zhang, Z., Robinson, D., & Tepper, J. 2020. Detecting

hate speech on Twitter using a convolution-GRU

based deep neural network. Social Network

Analysis and Mining, 10(1), 1–18.

AI-Powered Fraud Detection: A Comparative Study of Gradient Boosting Machines and Neural Networks