Predicting Nutrient Density in Foods Using Machine Learning

Models: A Comparative Study

Changhe Yang

Shanghai United International School, Wanyuan Campus, Shanghai, China

Keywords: Nutrition Density, Machine Learning, Regression Models.

Abstract: Fine-tuning and thus accurately estimating nutrition density in foods is useful in optimizing diets and

improving health standards. Several challenges have been observed with the traditional methods for nutrient

evaluation. Most of these challenges can be trimmed down by adopting the use of Machine Learning (ML)

models, which possess better capabilities of giving efficient and accurate assessments. To this end, different

regression models were applied to estimate nutrient density, namely Linear Regression, Ridge Regression,

Decision Trees, and Random Forests. The used set had 2397 food items for which 33 nutrients had been

deemed relevant. The missing values in the chosen dataset were addressed before model training through

imputation and normalization for better data quality. The models were trained and evaluated using separate

training and test sets, with performance indicators such as Mean Absolute Error (MAE) and R-squared (R²)

used to measure their accuracy. Results showed that linear models, such as Linear Regression and Ridge

Regression, achieved the best accuracy, with an R² of 0.999, while tree-based models exhibited overfitting

tendencies, resulting in lower predictive performance on unseen data. These findings demonstrate the

effectiveness of machine learning in predicting nutrition density, significantly improving the precision of

dietary recommendations.

1 INTRODUCTION

Dietary habits are now considered to be a vital part of

health promotion and maintenance, especially in the

etiology and prevention of chronic non-

communicable diseases such as obesity, type-2

diabetes, hypertension, and atherosclerosis associated

with unhealthy diets (Drewnowski, 2009). An

example is the laboratory analysis and nutrition

databases that are employed in the traditional

approach to evaluate nutritional quality. In response

to these problems, there is increasing concern about

artificial intelligence for improved assessments of

nutrition density in foods due to their superior

performance (Drewnowski et al., 2019). Machine

learning (ML), especially, shows great potential

advancements in delivering helpful dietary

recommendations to individuals, thus helping them

make the right decisions regarding their choice of

foods to take (Drewnowski, 2019).

The learning capability, intrinsic to machine

learning algorithms, has been illustrated with several

https://orcid.org/0009-0004-2160-0459

works on many tasks, and the same applies to

nutritional science. Conventional approaches seem to

have their limitations in this area, so it only makes

sense to attempt to use the relatively more advanced

machine learning technique. With big data, many

factors that are not easily observable or even

recognizable may be modeled and analyzed to predict

Nutrition Density more efficiently than in systems

that employ traditional analytics (Drewnowski,

2005). Explaining how nutrition density scores

balance overcrowded food product health claims with

Henley’s health-supporting mission, Drewnowski

best encapsulates the beneficial relationship between

health and food. Subsequent studies have established

that those machine learning algorithms can make

probable an undertaking of nutrition density by

evaluating several nutritional parameters including

fat content, sugar content, and vitamin and mineral

contents (Shen et al., 2020). Armand et al. (Armand ,

2024) described an inherent capability of ML within

nutrition science to transfigure the field through the

measurements of nutrition density and the provision

of personalized advice.

Yang and C.

Predicting Nutrient Density in Foods Using Machine Learning Models: A Comparative Study.

DOI: 10.5220/0013487500004619

In Proceedings of the 2nd International Conference on Data Analysis and Machine Learning (DAML 2024), pages 64-69

ISBN: 978-989-758-754-2

Furthermore, due to their capacity to work with

big and intricate data sets, the ML models are

especially useful for nutritional analysis, where more

conventional approaches might fail to capture the

associations of the different nutrients. For instance,

Lucas Prado Osco et al. (Osco, 2020), were able to

utilize machine learning to determine nutrition value

content in agricultural produce and this is a further

example of the application of these techniques. Also,

Timsina et al. (Timsina, 2021) presented how ML has

been useful in enhancing nutrition management in the

agriculture field; therefore, valid in the food and

health industries.

For an effective and precise estimation of

nutrition density, Linear Regression, Lasso

Regression, Ridge Regression, Decision trees,

Random Forest, and AdaBoost models are chosen in

this study. These models have been selected to

illustrate that they are distinct from each other, from

linear models through different types of ensemble

techniques. These linear models were particularly

effective when it came to the modeling of the

relations between features and nutrition density. In

assessing the performance of each model, specific

evaluation metrics were employed including Mean

Absolute Error (MAE), Mean Squared Error (MSE),

and R-squared (R²) to get a full analysis of the

models’ prediction potentials.

2 METHOD

2.1 Dataset Preparation

The dataset (Dey, 2024) used in this study was

meticulously designed to capture the detailed

nutritional profile of various food items, providing a

comprehensive foundation for predicting nutrition

density. The dataset includes 36 columns, each

representing a specific nutrient or related metric

essential for understanding the nutritional content of

the foods. These columns cover a wide range of

essential macronutrients, micronutrients, vitamins,

and minerals, which are critical for evaluating the

overall nutritional value of each food item.

The dataset consists of 2,397 rows, each

corresponding to a unique food item. To ensure robust

model training and evaluation, the dataset was

divided into two subsets: a training set and a test set.

The training set, containing 1,674 rows, was used to

train the machine learning models. The test set,

comprising 723 rows, was reserved for evaluating the

performance of the trained models. This separation of

data allows for an unbiased assessment of the model’s

predictive capabilities, ensuring that the models

generalize well to new, unseen data.

The dataset includes the following key columns:

 Caloric value: This column captures the total

energy provided by the food, measured in

kilocalories (kcal) per 100 grams. It serves as a

baseline for comparing nutrition density

relative to energy content.

 Carbohydrates: This includes both total

carbohydrates and sugars, highlighting the

presence of simple sugars, which can

significantly impact health outcomes.

 Vitamins and minerals: The dataset includes

detailed information on a wide range of

vitamins (A, B1, B11, B12, B2, B3, B5, B6, C,

D, E, K) and minerals (Calcium, Copper, Iron,

Magnesium, Manganese, Phosphorus,

Potassium, Selenium, Zinc), each measured in

milligrams per 100 grams. These nutrients are

vital for various bodily functions, from bone

health to immune support.

Last but not least, the Nutrition Density column is

the last column that serves as the nutrition richness of

the food per calorie. This column is significant for the

analysis as it goes to the heart of the study’s purpose

which is to predict nutrition density.

Again, before engaging in the analysis, the dataset

went through some basic exploratory data analysis

steps to clean the data. For the handling of missing

values, the proper imputation methods were used to

fill in the missing values and normalize the data set

was used to transform all the features into one

convenient scale. Such a preprocessing enables the

models to learn from alterations in the data without

being influenced by differences in feature scales, or

lack of missing values.

During the model training, the ‘Food’,

‘Identifier’, and ‘Nutrition Density’ feature columns

were omitted from the features because they are not

themselves predictors of nutrition density and are

categorical variables for food identification and target

variables respectively. This led to the use of 33

features, in total for developing the model used for

training the classifier. The rest of the columns given

the data offered the inputs to the machine learning

models while the Nutrition Density served as the

output.

Cutting the dataset into the training and testing

sets was done to enable a conclusive assessment of

the model’s accuracy. This means, the study was able

to keep a portion of the data for testing and could be

able to determine whether the model was overfitting

on the training data or it could perform well on foods

that were not imported into a model. This is common

Predicting Nutrient Density in Foods Using Machine Learning Models: A Comparative Study

in machine learning-oriented practices and it is very

important when it comes to creating models that

generalize to other situations.

2.2 Machine Learning Models-based

prediction

2.2.1 Linear Regression Models with

Variants

Linear Regression: Linear Regression is used as a

baseline model and notwithstanding its eccentricity in

finding linearity between the features and the target

variable it is simple. Although it might be less

accurate than other models of higher complexity, it is

valuable for its interpretability of the contributions of

the features. It is stated by Yao et al. (Yao, 2013) that

there are other methods such as using modal

regression; however, using Linear Regression is

inevitably simpler and more transparent while

obtaining shorter prediction intervals, even in cases

where the distribution is skewed.

Lasso Regression: Lasso Regression, uses L1

regularization hence solving the problem of data

overfitting, and does feature selection by setting

coefficients to zero. This method is especially useful

in big data, especially in a situation where there are

many independent variables to consider since it

reduces the possibility of making large prediction

errors and provides a measure of checking the

model’s complexity. According to Ranstam et al.

(Ranstam, 2020), even as it imposes potential bias in

estimating individual parameters, Lasso lends itself to

be an effective technique for obtaining high overall

accuracy in the prediction which is more desirable

when working with large numbers of predictors.

Ridge Regression: Ridge Regression makes use

of the L2 regularization to handle the issue of

multicollinearity between the features to ensure more

accurate computation of coefficients that leads to

better predictions. They include genetic data analysis

where the number of predictors surpasses the

observations, thus making it suitable for high

dimensions. By removing mean-square error for the

correlated predictors, as noted by Cule (Cule , 2013),

Ridge Regression can be used in cases where the

basic regression can be non-applicable while still

offering good predictive quality and stability.

For these regression models, the primary

hyperparameters to tune were the regularization

strength (denoted by alpha). Grid Search Cross-

Validation was employed to explore a range of alpha

values to determine the optimal regularization

parameter. This process involved systematically

testing multiple values of alpha and selecting the one

that minimized the validation error.

Grid Search: The Grid Search method

exhaustively searches over a specified parameter grid

for each model. For instance, in Ridge and Lasso

Regression, various alpha values were tested to find

the one that best balanced model complexity and

prediction accuracy.

Support Vector Machine (SVM) Regression:

SVM Regression examines possible non-linearity of

relationships between dependent and independent

variables by transforming the input data set by

various kernels. It is an advantage to provide high

accuracy, and at the same time, generalization was

pursued for data with many features for the number

of cases. However, as stated by Pisner (Pisner, 2020),

overfitting is common with SVM but it is still very

useful in many regression problems that pose both

linear and non-linear curvatures.

The SVM regression model required tuning of the

C parameter (regularization), the kernel type (e.g.,

linear, polynomial), and the gamma parameter (for

non-linear kernels). Again, Grid Search Cross-

Validation was used to explore combinations of these

parameters.

Grid Search: The grid search for SVM involved

testing different kernel functions and their respective

parameters (e.g., C and gamma). The combination

that provided the best cross-validation performance

was selected as the optimal model configuration.

For these regression models, the primary

hyperparameters to tune were the regularization

strength (denoted by alpha). Grid Search Cross-

Validation was employed to explore a range of alpha

values to determine the optimal regularization

parameter. This process involved systematically

testing multiple values of alpha and selecting the one

that minimized the validation error.

Grid Search: The Grid Search method

exhaustively searches over a specified parameter grid

for each model. For instance, in Ridge and Lasso

Regression, various alpha values were tested to find

the one that best balanced model complexity and

prediction accuracy.

2.2.2 Tree-based Model

Decision Tree: Decision Tree models work for data

with non-linear relations as segmentation of variables

forms a tree, thus, classifying the data. This is a non-

parametric approach technically capable of handling

large-sized data and missing values without requiring

strenuous assumptions. According to Song (Song,

2015), Some of the common uses of Decision Trees

include variable selection, testing of variable

importance, and making of forecasts which are

reasons why this method is prevalent, especially for

DAML 2024 - International Conference on Data Analysis and Machine Learning

medical research that requires simple models that are

easy to understand.

For the Decision Tree model, the hyperparameters

tuned included the maximum depth of the tree, the

minimum samples required to split a node, and the

minimum samples required at a leaf node. These

parameters control the complexity of the tree and

prevent overfitting.

Grid Search: Grid Search was applied to identify

the best combination of these parameters. By varying

the maximum depth, minimum samples split, and

minimum samples leaf, the grid search determined

the configuration that yielded the best validation

performance.

2.2.3 Ensemble Models

Random Forest: The decision tree is an individual

model; Random Forest is an advanced method that

combines many decision trees through an average that

minimizes the risk of over-fitting. It is a complex

calculation and not easy to decipher, but when it

comes to large and interaction-riddled data as well as

non-parametric analyses, it stands out. While

Random Forest may be known as the “black box”,

according to Rigatti (Rigatti, 2017), the abilities to

model non-linear effects make it important for many

predictive tasks.

The Random Forest model required tuning the

number of trees, the maximum depth of each tree, the

minimum number of samples required to split a node,

and the number of features to consider when looking

for the best split.

Randomized Search: Instead of an exhaustive grid

search, a Randomized Search Cross-Validation was

employed for Random Forest due to the larger

parameter space. This method samples a fixed

number of parameter settings from the specified

distributions and tests them, making it more efficient

for models with numerous hyperparameters.

AdaBoost: AdaBoost is an ensemble model

functioning as an enhanced weak learner through

weight assignment based on misclassifications of

instances. It transforms weak predictors into strong

models and it is among the best algorithms in data

mining since it has an impact on other learning

algorithms, according to Cao et al. (Cao, 2013). This

reconstruction based on the scores has made

AdaBoost to be a popular and successful tool in

machine learning.

For AdaBoost, the key hyperparameters tuned

were the number of estimators (i.e., the number of

weak learners to combine) and the learning rate

(which controls the contribution of each weak

learner). These parameters were optimized to

improve the ensemble's accuracy and reduce

overfitting.

Grid Search: Like other models, Grid Search

Cross-Validation was used for AdaBoost. The

method tested different values for the number of

estimators and the learning rate to find the

combination that resulted in the best model

performance.

2.3 Evaluation Metrics

To ensure the accuracy and reliability of the models

in predicting nutrition density, four key validation

metrics were employed. These metrics assess

different aspects of prediction accuracy and error

distribution, providing a comprehensive evaluation of

each model's performance. The validation was

performed on the test set, which contains data not

seen by the models during training. The metrics used

are as follows:

𝑀𝐴𝐸=

𝑛



𝑦



−𝑦











)

𝑀𝑆𝐸=

𝑛



(

𝑦



−𝑦





)









)

𝑅𝑀𝑆𝐸=



𝑛

(𝑦



−𝑦



)







)

𝑅



=1−

∑

(𝑦



−𝑦



)







∑

(𝑦



−𝑦



)







)

3 RESULT AND DISCUSSION

The Linear Regression, Ridge Regression, and SVR

models demonstrated excellent performance across

all metrics shown in Table 1. These models achieved

an R² value of 0.999, indicating nearly perfect

predictions on the test set. The MSE and RMSE

values for these models were extremely low (MSE:

0.002, RMSE: 0.040 for both Linear and Ridge

Regression), further confirming their accuracy. These

results suggest that linear models and SVR are highly

effective in capturing the relationship between the

features and nutrition density, making them reliable

choices for this predictive task.

Predicting Nutrient Density in Foods Using Machine Learning Models: A Comparative Study

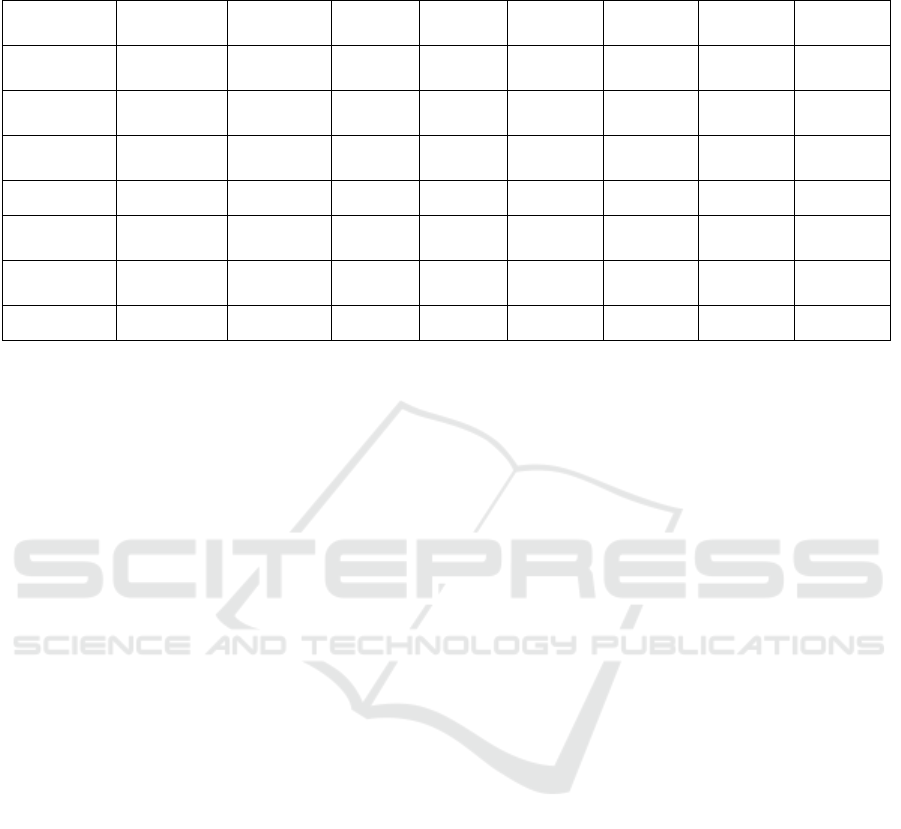
Table 1: Model Performance Metrics Summary

Train

MSE

Test

MSE

Train

𝑅



Test

𝑅



Train

MAE

Test

MAE

Train

RMSE

Test

RMSE

Linear

regression

0.001 0.001 0.999 0.999 0.018 0.022 0.033 0.039

Lasso

Regression

133.890 26.416 0.996 0.997 5.432 3.163 11.571 5.139

Ridge

Regression

0.001 0.001 0.999 0.999 0.018 0.022 0.033 0.039

SVM

543.093 774.441 0.985 0.939 9.855 12.859 0.033 27.828

Decision

Tree

1396.349 424.893 0.961 0.966 4.918 7.515 23.304 20.612

Random

Forest

3288.969 2766 0.910 0.783 43.877 41.752 57.349 52.597

Adaboost

0.006 0.004 0.999 0.999 0.053 0.051 0.079 0.069

On the other hand, the Decision Tree and Random

Forest models, while performing well on the training

data, exhibited signs of overfitting. The Decision Tree

model, for example, had a significantly higher test

MSE of 774.441 and an R² of 0.939, which, although

still relatively high, indicates a drop in performance

compared to the linear models. Similarly, the Random

Forest model had a test MSE of 424.893 and an R² of

0.967. These figures suggest that while tree-based

models can capture complex interactions within the

data, they may struggle with generalization,

particularly when not properly tuned.

The AdaBoost model struggled significantly in

this application. It had the highest test MSE of

2766.445 and the lowest R² value of 0.783 among all

models tested. The MAE and RMSE were also much

higher compared to other models, indicating that

AdaBoost was not well-suited for predicting nutrition

density in this dataset. This poor performance could

be due to AdaBoost's sensitivity to noisy data or its

tendency to overfit, especially in the absence of

strong individual learners.

The success of machine learning in predicting

nutrition density in fruits is supported by similar

studies, such as the prediction of fiber content in

Australian packaged foods using the k-nearest

neighbors (KNN) algorithm. This study found that

KNN significantly outperformed manual prediction

methods with an R² value of 0.84, highlighting the

potential of machine learning to predict important

nutritional metrics efficiently, according to Davies et

al. (Davies, 2021). In research, models like Linear

Regression and Ridge Regression achieved even

higher accuracy, demonstrating that machine learning

can be a robust tool for various nutritional

predictions.

Interestingly, this work reveals that simple

models: Linear Regression, Ridge Regression, and

SVR have higher accuracy rates than complex

models: Decision Tree, Random Forest, and

AdaBoost for nutrition density. This may have caused

a higher performance of these models because a linear

flow of data makes it easy for models not to overfit

while training by establishing the relationship that

exists between features and the target variable. It is

quite evident that these models have great

generalization ability, especially by looking at how

well they have performed on both training and test

sets.

On the other hand, the Tree Models, much as they

are capable of handling nonlinearity and interaction,

had the vice of overfitting the data. This is usually the

case when models learn noise within the training data

and not the repeated patterns thus affecting the

generalization of new data. The AdaBoost model has

shown poor results, which can be attributed to the

relative sensitivity to noise and the difficulty of

combining several weak learners.

Therefore, this study has shown that different

models’ selection should be determined and guided

by the characteristics of the given dataset. Compared

to more complex models, the simpler ones might

perform better, especially when the linear relationship

prevails between the features and the target variable.

In more complex models there can be the problem of

overfitting, which reduces the ability of these models

to be effective. One could take up future research on

the hybrid approaches or the incorporation of more

features to develop better the performance of non-

linear models in similar predictive tasks.

4 CONCLUSIONS

This research was able to use machine learning

models to accurately predict nutrition density in food,

and thus show that ML could be of great value in

DAML 2024 - International Conference on Data Analysis and Machine Learning

boosting the analysis of diets. Regression analysis,

especially linear regression, as well as ridge

regression, decision trees, Random forests, and other

models, were used to compare and contrast various

factors to nutrition density. Based on the obtained

experimental results, it was found that Linear

Regression models including Linear Regression and

Ridge Regression exhibit the highest accuracy with

the value of R² of a nearly perfect degree of 0.999. It

also shows that machine learning is more useful in

dealing with a massive dataset and is generally

reliable in enhancing the forecasted probability as

compared to the simple nutritional analysis which

took a lot of time and resources.

Therefore, the research outcomes show the

applicability of machine learning algorithms for

determining nutrition density so that better and

evidence-based dietary advice could be given.

However, it also emerged that Decision Trees and

Random Forest others may encounter problems such

as overfitting which infers that further tuning or

perhaps the use of a hybrid model could be

considered. Subsequent studies may also look at

extending the existence of other features or the raw

employ of superior models, to enhance the exactness

of predictive operations as well as the reductions in

nonlinear data sets.

REFERENCES

Armand, T., Kintoh Allen Nfor, Kim, J.-I., & Kim, H.-C.

2024. Applications of Artificial Intelligence, Machine

Learning, and Deep Learning in Nutrition: A

Systematic Review. Nutrients, 16(7), 1073–1073.

Cao, Y., Miao, Q.-G., Liu, J.-C., & Gao, L. 2013. Advance

and Prospects of AdaBoost Algorithm. Acta

Automatica Sinica, 39(6), 745–758.

Cule, E., & De Iorio, M. 2013. Ridge Regression in

Prediction Problems: Automatic Choice of the Ridge

Parameter. Genetic Epidemiology, 37(7), 704–714.

Davies, T., Louie, J. C. Y., Scapin, T., Pettigrew, S., Wu, J.

H., Marklund, M., & Coyle, D. H. 2021. An Innovative

Machine Learning Approach to Predict the Dietary

Fiber Content of Packaged Foods. Nutrients, 13(9),

3195.

Dey, U. 2024. Food Nutrition Dataset. Kaggle.com.

https://www.kaggle.com/datasets/utsavdey1410/food-

nutrition-dataset/data

Drewnowski, A. 2005. Concept of a nutritious food: toward

a nutrient density score. The American Journal of

Clinical Nutrition, 82(4), 721–732.

Drewnowski, A. 2009. Defining Nutrient Density:

Development and Validation of the Nutrient Rich

Foods Index. Journal of the American College of

Nutrition, 28(4), 421S426S.

Drewnowski, A. 2019. Impact of nutrition interventions and

dietary nutrient density on productivity in the

workplace. Nutrition Reviews, 78(3), 215–224.

Drewnowski, A., Dwyer, J., King, J. C., & Weaver, C. M.

2019. A proposed nutrient density score that includes

food groups and nutrients to better align with dietary

guidance. Nutrition Reviews, 77(6), 404–416.

Lucas Prado Osco, Paula, A., Pinheiro, F., Saito, A., Nilton

Nobuhiro Imai, Nayara Vasconcelos Estrabis, Ianczyk,

F., Fernando, Veraldo Liesenberg, Jorge, Li, J., Ma, L.,

Wesley Nunes Gonçalves, José Marcato, & José

Eduardo Creste. 2020. A Machine Learning Framework

to Predict Nutrient Content in Valencia-Orange Leaf

Hyperspectral Measurements. Remote Sensing, 12(6),

906–906.

Pisner, D. A., & Schnyer, D. M. 2020. Chapter 6 - Support

vector machine (A. Mechelli & S. Vieira, Eds.).

ScienceDirect; Academic Press.

Ranstam, J., & Cook, J. A. 2016. Overfitting. British

Journal of Surgery, 103(13), 1814–1814.

Rigatti, S. J. 2017. Random Forest. Journal of Insurance

Medicine, 47(1), 31–39.

Shen, Z., Shehzad, A., Chen, S., Sun, H., & Liu, J. 2020.

Machine Learning Based Approach on Food

Recognition and Nutrition Estimation. Procedia

Computer Science, 174, 448–453.

Song, Y.-Y., & Lu, Y. 2015. Decision tree methods:

applications for classification and prediction. Shanghai

Archives of Psychiatry, 27(2), 130–135.

Timsina, J., Dutta, S., Devkota, K. P., Chakraborty, S.,

Neupane, R. K., Bishta, S., Amgain, L. P., Singh, V. K.,

Islam, S., & Majumdar, K. 2021. Improved nutrient

management in cereals using Nutrient Expert and

machine learning tools: Productivity, profitability, and

nutrient use efficiency. Agricultural Systems, 192,

103181.

Yao, W., & Li, L. 2013. A New Regression Model: Modal

Linear Regression. Scandinavian Journal of Statistics,

41(3), 656–671.

Predicting Nutrient Density in Foods Using Machine Learning Models: A Comparative Study