Solving Some Economic Issues Using Innovative Methods

Kholbozorov Kuvonchbek

1,2

National University of Uzbekistan named after Mirzo Ulugbek, University street-4. Tashkent, Uzbekistan

International School of Finance Technology and Science Institute, University Street-2. Kibray District, Tashkent,

Uzbekistan

Keywords: Mathematics, GeoGebra, Economic, Innovative.

Abstract: The article provides instructions on how to solve economic problems in the nonlinear programming

department of "Mathematics for Economists" using an innovative approach. The graphical environment of

GeoGebra was used to solve the problem. The solution to the problem was found visually.

1 INTRODUCTION

Linear programming is a branch of mathematical

programming that seeks to maximize profits or

minimize costs by rationally allocating limited

resources (raw materials, equipment, land, water,

fertilizers, etc.). teaches

The formation of linear programming had a major

impact on the development of economic thought in

the second half of the twentieth century. The

awarding of the Nobel Prize to the Russian scientist

LV Kantorovich, who first discovered the theory of

linear programming in 1975, and the mathematician

in economics, the first author of the term "linear

programming", the American scientist T.Ch. can be

considered as.

The linear programming method allows you to

search for and find the largest and smallest values of

a linear function when limiting conditions are placed

on the unknowns that are part of it.

As you know,

(, ,..., ) , ( 1,)

ini

qxx x b i m≤=

(1)

(, ,..., ) max

Zfxx x=→

(2)

The study of conditions under a single system is

called mathematical programming.

If at least one of the functions involved in problem

(1), (2) is a nonlinear function, then the problem is

called a "nonlinear programming problem"

(Xashimov, Xujaniyozova, Sotvoldiyev, and

Xolbozorov, 2022). There is no single way to find the

optimal solution to a nonlinear programming

problem. This can be seen as one of our efforts to find

a convenient way to find the optimal solution to

nonlinear programming problems.

We set ourselves the task of finding the optimal

solution to nonlinear programming problems using

GeoGebra, a multifunctional program that is

convenient for drawing various geometric shapes,

creating objects, working with function graphs, as

well as various statistical models.

GeoGebra is a dynamic math program for all

levels of education that combines geometry, algebra,

spreadsheets, graphics, statistics, and calculations in

a single engine. In addition, GeoGebra offers an

online platform with over 1 million free classroom

resources created by our multilingual team. These

resources can be easily shared through our

collaboration platform GeoGebra Classroom where

student progress can be tracked in real time.

GeoGebra is a community of millions of users located

in almost every country. It has become a leading

provider of dynamic math applications supporting

science, technology, engineering and mathematics

(STEM) education and innovation in teaching and

learning around the world. The GeoGebra math

engine supports hundreds of educational websites

around the world in a variety of ways, from simple

demonstrations to fully online assessment systems

(G'ulomov et al. 2019).

Kuvonchbek, K.

Solving Some Economic Issues Using Innovative Methods.

DOI: 10.5220/0013451800004654

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 4th International Conference on Humanities Education, Law, and Social Science (ICHELS 2024), pages 179-183

ISBN: 978-989-758-752-8

179

2 LITERATURE REVIEW

The work of Academician Gulyamov (Rasch, 2017)

and others is to teach future economists the use of

information systems in various sectors of the

economy and the use of automated information

technology in management. This textbook explores

the conceptual aspects of automation. Automated

information systems, information security and their

classification are considered. Special attention was

paid to automated information technologies and

software used in accounting, taxation and taxation,

banking, management, treasury and insurance

activities. In the digital economy, the focus is on the

information security of existing electronic banking

payment systems. The main directions of the use of

digital platforms in the information complexes of the

economy, including e-commerce, e-government,

cryptocurrency and digital money are widely

interpreted. The LMS and CMS systems covered in

the distance learning courses are covered in detail.

The textbook is intended for students, masters,

doctoral students and teachers studying information

science and technology in economics.

Indian scientist G. Rasch in his research has

shown that the main purpose of teaching the subject

of "Computer Graphics" should be to develop

creative activity in students to design production

problems on a computer (Erig, 2014).

Although Spanish scientists L.T.Erig (Chery,

2015), H.J.Chery (David, 2014), R.L.David (Zuo,

2013) have conducted research on the use of three-

dimensional interactive graphics to teach equipment

manufacturing processes, “ He tried to use three-

dimensional modeling in teaching the subject of

"Computer Graphics", but did not study enough

issues such as the development of spatial imagination

of students, the development of creative activity in

computer design.

Analysis of the research shows that the problem

of developing a model for the development of

creative activity of students and the design of

teaching methods in higher education institutions

(HEIs) using the capabilities of various graphics

programs in the teaching of "Computer Graphics" has

not been studied. rsatdi. The lack of scientific and

pedagogical solutions to these problems means that

students do not fully understand the purpose and

content of teaching computer graphics in universities,

lack of spatial imagination in modeling issues of their

specialization using the capabilities of various

graphics programs, "Drawing geometry and

Engineering Graphics” is an integral part of the

subject“ Computer Graphics ”. Korean scientist Z.

Zuo (Daxer, 2013) conducted research on the

introduction of computer technology and

improvement of teaching in the teaching of

"Computer Graphics". In his research, he argued that

"Descriptive Geometry and Engineering Graphics"

should be conducted in conjunction with "Computer

Graphics."

In his dissertation research VS Kornilov

(Tixobayev, 2012) believes that the most important

task of pedagogy is to find, collect and analyze

various technologies and methods of using teaching

aids in the educational process in such a way as to

give them the characteristics of fitness for production.

The introduction of information technology in

education, in particular computer mathematics

packages, into the learning process begins to shape

students ’computer visual thinking, which includes

the management of images on a computer screen.

Students are given the opportunity to actively and

consciously understand a variety of mathematical

concepts that were previously unfamiliar; successful

solution of educational mathematics problems.

From a pedagogical point of view, YA Daxer

believes that the computer mathematics set is a

didactic teaching tool that allows optimizing the

learning process when an appropriate teaching

methodology is available. Informatics is a tool

designed to automate the solution of mathematical

problems in various fields of science, technology and

education, combining a modern user interface,

analytical and numerical methods for solving various

mathematical problems, tools for visualizing the

results of calculations. At the decision-making stage,

such a tool allows for a more reliable analysis of the

results obtained.

In his article, AG Tikhobayev called for the use of

modern computer technology for professional self-

education of students. Interactive computer

technology allows you to acquire not only theoretical

knowledge but also practical skills. In the context of

the introduction of new information technologies, this

problem is especially relevant.

3 RESULTS AND DISCUSSION

In his work, KH Kholbozorov gave methodological

recommendations on the advantages and

disadvantages of GeoGebra over other mathematical

programs, as well as on how to facilitate students'

imagination when using GeoGebra in teaching

Mathematics for Economists.

KH Kholbozorov studied the geometric

interpretation of economic problems using the

ICHELS 2024 - The International Conference on Humanities Education, Law, and Social Science

180

program "GeoGebra". In order to show the

appropriateness of the application of the program

"GeoGebra" in practice, the geometric interpretation

of linear, nonlinear problems in space was studied,

and methodological recommendations for the

application of this program were given.

The article by AG Abdurahmanov discusses the

relevance of the use of mathematical packages in the

learning process. Universal math kits create new

opportunities to improve education, without

exception, its stages. Problems related to the use of

mathematical packages and ways to solve these

problems are also noted. As an example, the graphical

solution of non-standard equations using the Maple

program is considered.

In the research work of AV Nesterova,

mathematical sets significantly facilitate the learning

activities of students. Their use allows you to avoid

the need to perform large mathematical calculations

manually, overcome difficulties in solving economic

and mathematical problems and analyze the results

obtained, easily prepare reports on laboratory work,

present calculations in graphical form.

In the work of YV Mazurenko the issues of

teaching the subject of "Higher Mathematics" to 1st

year students using computer programs are

considered. Features of using different computer

programs in multi-stage initial preparation of students

are considered. It turns out that computer packages

are not used intensively in the educational process,

despite their great educational potential. The

possibilities of using both specialized math packages

and the most common office applications were

analyzed. First-year students of technical colleges are

given the opportunity to use mathematical programs

in the study of "Linear Algebra".

In her research, IV Belenkova noted that computer

mathematics packages allow students to creatively

solve problems in the following areas: mathematical

modeling, probability theory, mathematical statistics,

numerical methods, linear programming,

optimization methods, mathematical analysis,

geometry, integral and differential equations, etc.

In his monograph, VM Monakhov writes that

computer technology develops thinking skills, basic

computer skills, the ability to acquire and apply basic

knowledge in the field of computer science and

modern information technology, the ability to work

independently and in a team.

Fractional linear economic problems are

encountered in production problems. In solving such

problems comes the problem of finding the

maximum, minimum of the given problems. If the

function is complex, it is almost impossible to solve

it analytically. In this case, it is advisable to solve the

problem graphically. For example, consider the

following issue in the case of I.L. Akulich. Here are

some ways to solve economic problems using an

innovative approach, namely the GeoGebra program.

Issue. In the account of firm A 12 sh.p. There is

unit money. The prices of x, y and z raw materials are

1, 2 and 3 sh.p. currency. Using the money in the

account, find the x, y, and zs that maximize the profit

function.

Solution. According to the terms of the case, and

the unit price of raw materials is equal to 1.2 and 3

shs, respectively. It will be in the form of total costs,

for which the company plans to spend 12 shs. So, the

mathematical model of the problem is as follows.

2312

0, 0, 0

xyz

++=





≥≥≥



0.2 0.3 0.5

maxQxyz=→

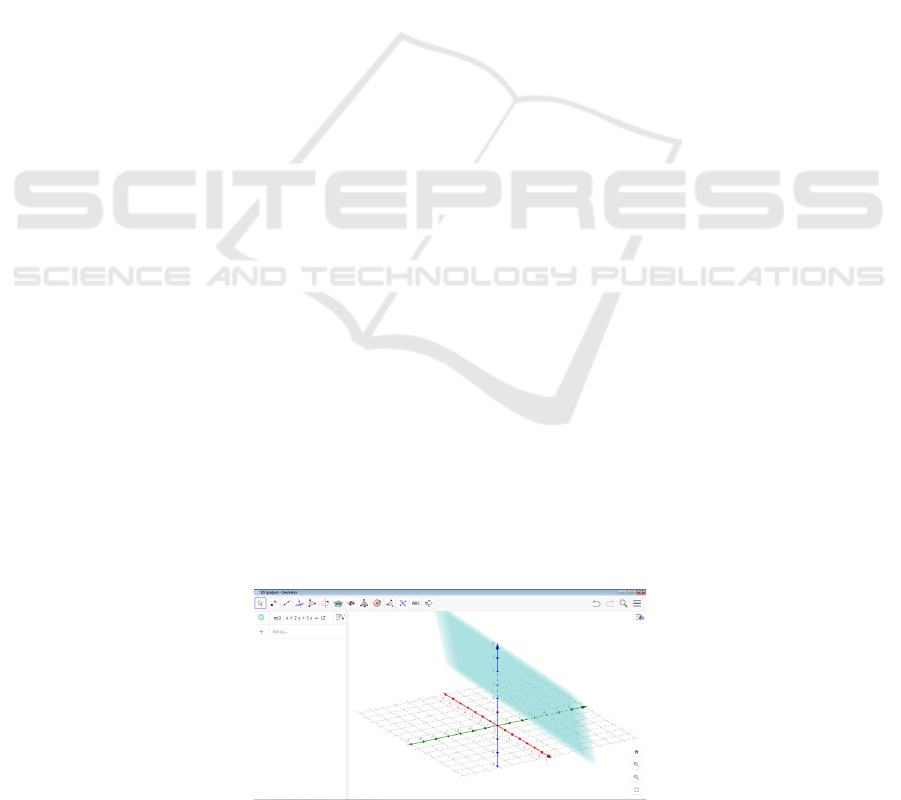
We will solve this problem using GeoGebra. To do

this, first run GeoGebra, go to the 3D Graphics

section and draw a plane (Figure 1).

To draw the target function, open the 2D Graphics

section and enter the parameter change intervals from

the Slider command. For example, we define the

range of variation a from 0 to 5 (Figure 1).

Then we equate the objective function to

parameter a and find z from it. From this we get the

equation and draw the surface outside the 2D

Graphics section (Figure 2).

Figure 1: Plain.

Solving Some Economic Issues Using Innovative Methods

181

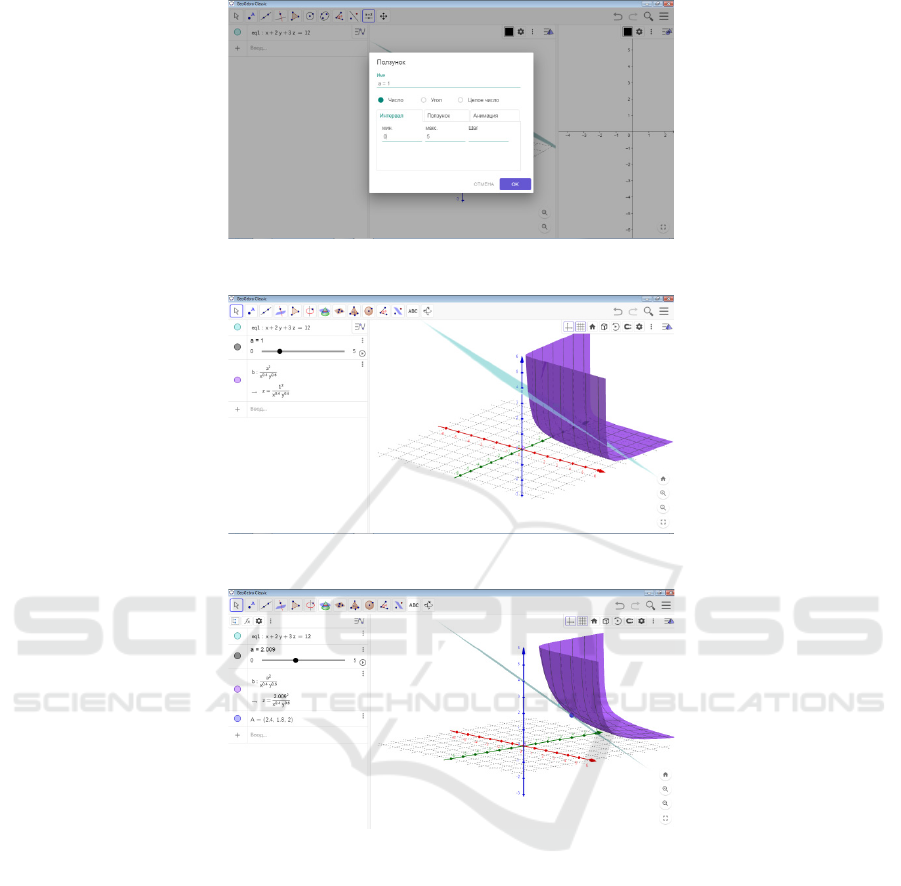
Figure 2: Parameter

Figure 3: Surface and plane

Figure 4: Plane and surface test point.

As can be seen from the diagram above, the plane

and the surface intersect. This means that it is not the

optimal solution. We need to find the point where the

surface touches the plane. To do this, we start

changing the parameter and stop the parameter when

we reach the desired location. If we denote the point

of impact by A, we can see its coordinates (Figure 4).

If necessary, we can refine the graph to see the

coordinates of point A with sufficient accuracy.

Figure 4 shows that the maximum gain is

approximately 2.0097, x = 2.4, y = 1.8, and z = 2.

4 CONCLUSION

In this work, the graphical environment of the

program "GeoGebra" was used to solve economic

problems in the field of nonlinear programming in

"Mathematics for Economists" with the help of

innovative approaches.

In the first problem presented in the article, the

field is a polygon, and if you need to check each end

for optimality in the classical methods to find its

optimal solution, it is shown that the optimal solution

can be obtained visually in the method we propose.

The optimal solution of the second problem above

is a solution of a system of nonlinear equations in

ICHELS 2024 - The International Conference on Humanities Education, Law, and Social Science

182

classical methods, the solution of which is based on

complex calculations to find the solution due to

nonlinearity, and the method we propose shows that

the optimal solution can be obtained graphically.

For economists, the use of innovative methods in

teaching mathematics can save time, broaden the

horizons, and visualize the solution.

REFERENCES

Abduraxmanov. (2021). Primeneniye matematicheskix

paketov v obrazovanii na primere matematicheskogo

paketa Maple. "Ekonomika i sotsium" № 3(82).

Retrieved from www.iupr.ru

Akademik S.S.G‘ulomov va boshqalar. (2019).

Iqtisodiyotda axborot komplekslari va texnologiyalari.

Darslik. T.: “Fan va texnologiya”, 448 bet.

Akulich, I.L. (1986). Matematicheskoe programmirovanie

v primerax i zadachax: Uchebnoe posobie dlya vuzov.

M.: Visshaya shkola., 214-216 str.

Askarov, X., Karimov, I., Mirzayeva, U., & Askarova,

M.B. (2024). Rectification column laboratory device

physical dependence on plate structures experimental

determination. E3S Web of Conferences, 538, 01032.

https://doi.org/10.1051/e3sconf/202453801032

Belenkova, I.V. (2004). Metodika ispolzovaniya

matematicheskix paketov v professionalnoy

podgotovke studentov vuza dis. kand. ped. nauk:

13.00.08: Yekaterinburg, 261 s.

Chery, H.J. (2015). Animation and computer graphics.

AQSH, 90 pp.

Daxer, Ye.A. (2013). Nekotorie aspekti bilingvisticheskoy

modeli obucheniya matematicheskim dissiplinam

studentov ekonomicheskogo profilya. Kiyev: Gnozis,

Tom 5.

David, R.L. (2014). Visualisation and animation of

computer graphics. Korea, 105 pp.

Erig, L.T. (2014). Construction of 3D modeling. Ispania, 34

pp.

G‘ulomov, S.S. va boshqalar. (2019). Iqtisodiyotda axborot

komplekslari va texnologiyalari. Darslik. T.: “Fan va

texnologiya”, 448 bet.

Kholbozorov, Q.X. (2020). Iqtisodga doir masalalarni

yechishda “GeoGebra” dasturidan foydalanish. “Fizika,

matematika va informatika”, (3), 29-37 pp.

Kholbozorov, Q.X. (2021). “Iqtisodchilar uchun

matematika” fanini o‘qitishda “GeoGebra” dasturining

qulayliklari. O’zMU xabarlari, № 2021.1.5, 147-150

pp.

Makhmudov, S., Askarova, M.B., Xasanov, D., & Askarov,

X. (2024). Features of accounting for nonlinear work of

reinforced concrete in calculations. E3S Web of

Conferences, 538, 01033.

https://doi.org/10.1051/e3sconf/202453801033

Makhmudov, S.M., & Abduraimova, K.R. (2020).

Innovative designs and technologies in foundation

engineering and geotechnics. International Journal of

Scientific and Technology Research, 9(1), 3803-3807.

Mamarajabov, M.E. (2022). Improvement of professional

and pedagogical training of future teachers in the

conditions of digitized education: Ped. science. doc. ...

autoref. – T.: 2022. – 78 p.

Monaxov, V.M. (2006). Vvedeniye v teoriyu

pedagogicheskix texnologiy: Monografiya. Volgograd:

Peremena, 345 s.

Rakhimov, R., Askarov, X., Abdullayev, I., & Kamilova,

O. (2024). Local in the conditions cheap and quality

construction materials complex working exit. E3S Web

of Conferences, 538, 01030.

https://doi.org/10.1051/e3sconf/202453801030

Rasch, G. (2017). Probabilistic Models for Some

Intelligence and Attainment Tests. Chicago: Univ. of

Chicago Press, p.199.

Sadriddin, S., Miralimov, M.M., Makhmudov, S.M., &

Akhmadiyorov, U.S. (2019). Modern methods of

increasing energy efficiency of buildings in the

Republic of Uzbekistan at the design stage.

International Journal of Scientific and Technology

Research, 8(11), 1333-1336.

Tillaev, A.I. (2020). Improving the teaching of

"Information Technology" in higher education on the

basis of multimedia technologies. European Journal of

Molecular & Clinical Medicine, 7(2).

Tixobayev, A.G. (2012). Interaktivnie kompyuternie

texnologii obucheniya. VestnikTGPU (TSPU Bulletin),

8(123).

Xashimov, A., Xujaniyozova, G., Sotvoldiyev, A., &

Xolbozorov, Q. (2022). Iqtisodchilar uchun

matematika. Darslik. T.: “IQTISOD-MOLIYA”, 315

bet.

Zainabidinov, S.Z., & Madaminov, Kh.M. (2020). Charge

transport mechanism INp-Si-n-(Si2)i-

x(CdS)xSemiconductor structures. Herald of the

Bauman Moscow State Technical University, Series

Natural, (4), 58–72.

Zuo, Z. (2013). Engineering computer graphs and

animation 3D modeling. Korea, 56 pp.

Solving Some Economic Issues Using Innovative Methods

183