Hydraulic Resistance to Air Flow in Drum Dryers

Rasuljon Tojiev

, Adil Akhunbayev

, Raxmatillo Mirsharipov, Nargiza Rajabova,

Abdurahmon Sulaymanov, Bobojon Ortiqaliyev, Gulmirakhon Madaminova,

Abdulloh Abdulazizov, Bekzod Alizafarov and Gulnoraxon Khasanova

Fergana Polytechnic Institute, Uzbekistan

Keywords: Drying, Hydraulic, Mineral, MATLAB.

Abstract: The article examines the hydraulic resistance during drying of mineral fertilizer at the outlet of a drum dryer.

From the analysis of existing designs of nozzles , their operating parameters were analyzed based on multi-

stage system analysis based on the MATLAB program, and an improved design scheme for a two-component

nozzle was developed. Based on the obtained regression equation, the optimal parameters for the values of

the determined criteria were determined: dryer performance, nozzle angle, coolant speed and coolant

temperature.

1 INTRODUCTION

Drying materials is one of the most energy-intensive

processes in a production line. Using this process is

important in determining the quality of the finished

product. The cost of thermal drying is 10% of the total

cost of the technological process. In this context, it is

important to create highly efficient, energy-saving

drying modes, as well as regulation and optimization

of heat exchange processes in dryers.

It is known from the literature that the drying

process depends on the size of the material, humidity,

hydrodynamics of movement of the material and the

drying agent, parameters of the internal and external

environment (Tang, 2003; Romanko & Frolov, 1990;

Pavlysh et al., 2013; Koraboev, 2022). The

combination of these factors determines the

conditions of the drying process. Therefore, various

methods and devices are used in industry depending

on the physical, chemical and mechanical properties

of the material to be dried. The most common is the

convective drying method, which is characterized by

the simplicity of the design of drum dryers used in

this process, high productivity and versatility.

Therefore, the trend of using these drying units in

various industries is growing, but this type of dryer

https://orcid.org/0000-0001-6764-3690

https://orcid.org/0000-0000-0002-7020

also has its disadvantages. For example, some

complex processes can be mentioned, such as

ensuring drying intensity, rational use of the coolant

used for drying, optimizing hydrodynamic

parameters and minimizing energy costs. Therefore,

the issues of determining and justifying the optimal

parameters in this type of device are relevant. Many

studies have been conducted to determine the optimal

parameters of these factors (Tang, 2003). However,

the presented data on the hydrodynamics of the dryer

and the optimal parameters of heat exchange

processes are different and sometimes contradict each

other.

It is known that when drying materials in industry,

two types of heat exchange are used - contact and

convective. However, a large amount of heat is

transferred to the dried material through convective

heat exchange. The amount of heat transferred by

convection to the material to be dried in a drum

apparatus is up to 20 times higher than the amount of

heat transferred by contact. The intensity of

convective heat transfer in the dryer, in turn, directly

depends on the opening of the particle surface and the

average particle size. The more material is distributed

over the drying surface, the greater the area of

convective

heat exchange. Thus, the efficiency of

Tojiev, R., Akhunbayev, A., Mirsharipov, R., Rajabova, N., Sulaymanov, A., Ortiqaliyev, B., Madaminova, G., Abdulazizov, A., Alizafarov, B. and Khasanova, G.

Hydraulic Resistance to Air Flow in Drum Dryers.

DOI: 10.5220/0013425200004654

In Proceedings of the 4th International Conference on Humanities Education, Law, and Social Science (ICHELS 2024), pages 779-785

ISBN: 978-989-758-752-8

779

1-drum body; 2-first part of the nozzle; 3-second part of the nozzle

Figure 1: Installation diagram of the proposed nozzle on the drum.

Figure 2: General view of the drum dryer.

drying materials in a drum dryer depends on the

surface layer of material falling from the dryer

nozzles. In turn, ensuring that the material scatters

over the internal section of the drum will depend on

the design of the contact element (Romanko &

Frolov, 1990; Su et al., 2015).

Although the simplicity, high efficiency and

versatility of the design of drum dryers allow them to

be widely used in various sectors of the national

economy, there are issues such as increasing the

intensity of the drying process, reducing hydraulic

resistance in the device, rational use of the heating

agent and minimizing energy consumption still

require research.

2 EXPERIMENTAL PROCEDURE

Based on existing designs of nozzles , their operating

parameters were analyzed on the basis of a multi-

stage system analysis based on the MATLAB

program, and an improved design scheme for a two-

component nozzle was developed (Pavlysh et al.,

2013) (Figure 1).

Based on system analysis, theoretical studies of

the hydrodynamic modes of a drum dryer were

carried out, a mathematical model of the drying

process was developed, the heat balance of thermal

drying of dispersed materials in a drum dryer,

methods for calculating heat and mass transfer

coefficients and optimizing the drying process

(Pavlysh et al., 2013).

In this article, based on the results of theoretical

studies, the parameters affecting the intensity of heat

transfer at low energy consumption using a two-

element nozzle in a drum dryer are experimentally

determined, as well as the influence of hydraulic

resistance and coolant velocity on the temperature of

the material (Aghbashlo et al., 2015; Brammer, 1999;

Khoshkava, 2014).

To assess the influence of the nozzle design on the

hydrodynamic parameters of the apparatus and heat

transfer processes, a laboratory drum dryer was

developed and experiments were carried out (Figure

2). The experiments were carried out in two stages

(Janowicz et al., 2018; Le Bissonnais, 1989; Sharma

et al., 2014).

3 RESEARCH RESULTS

At the first stage, the hydraulic resistance of a drum

ICHELS 2024 - The International Conference on Humanities Education, Law, and Social Science

780

with a two-section nozzle was studied. For the

research, the following limits of variable parameters

were selected: nozzle angle inclination R=15; 30 va

, number of heat exchange zones - 5, number of

nozzles in one row - 10 (nozzles are arranged in zones

in a checkerboard pattern), Speed of the coolant (air)

leaving the heater υ=1.4÷14.2 m/s, Productivity

devices Q

=0.18÷0.46 kg/s, Angle of inclination of

the drying drum relative to the plane α = 2.24 degrees

(according to technological regulations), rotation

speed of the drum dryer was set to n = 2.5; 3; 3.5 and

4 rpm. Tashki ҳ aroat gas va suv tizimi uchun 20 ±2

From tanlandi. Namuna materiali siphatida

superphosphate mineral ugiti tanlandi. The ambient

temperature was 20±2°C. Superphosphate mineral

fertilizer [superphosphate regulation] was chosen as

the experimental material.

The coefficients of hydraulic resistance of the

working bodies influencing the flow of coolant in the

dryer were determined experimentally from the

difference in the velocities of the inlet and outlet gas

in the apparatus and were solved according to the

proposed equation (Romanko & Frolov, 1990).

The obtained theoretical and experimental values

were compared and correction factors were

introduced. Empirical formulas were obtained by the

least squares method. The resistance coefficients

affecting the coolant flow in a drum dryer with a two-

section nozzle are given below.

According to the results of experiments at R= 15

and at apparatus productivity at 0.02 kg/s, the

coefficient is ξ= 3.34, at apparatus productivity at

0.03 kg/s, the coefficient is equal to ξ= 3.52 and at

apparatus productivity at 0 .04 kg/s the coefficient is

ξ= 3.74. According to the results of experiments at

R= 30

and at apparatus productivity at 0.02 kg/s, the

coefficient is ξ= 4.66, at apparatus productivity at

0.03 kg/s, the coefficient is ξ= 4.81 and at apparatus

productivity at 0.04 kg/s coefficient is ξ= 5.07.

According to the results of experiments at R= 45

and

at apparatus productivity at 0.02 kg/s, the coefficient

is ξ= 5.91, at apparatus productivity at 0.03 kg/s, the

coefficient is ξ= 6.09 and at apparatus productivity at

0.04 kg/s coefficient is ξ= 6.31. The error between

theoretical and experimental studies did not exceed

5%.

The total hydraulic resistance of the apparatus was

determined experimentally at various values of

variable factors. In the experimental determination of

hydraulic resistance, an electronic measuring device

JM-510 was used, which was compared with the

theoretical values determined by equation (4) and

plotted on a graph (Figures 3, 4 and 5).

As can be seen from the data presented in Figures

3; 4 and 5 , at a gas speed υ= 1.4÷14.2 m/s at an

interval step of 2.65 m/s and at a productivity Q =

0.02 ÷ 0.04 kg/s at an interval step of 0.14 kg /s, with

a slope of the bulk part of the nozzle R = 15 o

the

minimum value of hydraulic resistance was ΔP = 2.11

Pa, and the maximum value of hydraulic resistance

was ΔP = 262.6 Pa. Under similar conditions, with a

slope of the bulk part of the nozzle R = 30

the

minimum value of hydraulic resistance was ΔP = 3.65

Pa, and the maximum value of hydraulic resistance

was ΔP = 426.5 Pa. Under similar conditions, with a

slope of the bulk part of the nozzle R = 45

the

minimum value of hydraulic resistance was ΔP = 5.23

Pa, and the maximum value of hydraulic resistance

was ΔP = 583.09 Pa. Empirical formulas were

obtained to adequately describe the process using the

least squares method for the graphical relationships

shown in Figures 3-5.

At the second stage, the effect of coolant velocity

on the temperature of the material was studied.

Experiments were carried out on a laboratory

installation to determine the kinetic curves of the

drying process of mineral fertilizers. For the research,

the following values of variable parameters were

selected: drum productivity G

= 0.02; 0.03; 0.04

kg/s, coolant speed in the drum υ = 1.4÷14.2 m/s and

drum speed n = 2.5; 3.0; 3.5; 4.0 rpm

In the experiment, the initial parameters had the

following values. The initial moisture content of pre-

moistened mineral fertilizers was 20%. The initial

temperature of the coolant leaving the heater was set

at 100°C. The air temperature at the inlet and outlet

of the drum was measured with an ANEMOMETER

BA06–TROTEC device. The initial temperature of

the material was measured with a TS-4 thermometer.

The temperature at which the dried material enters the

drum was 21°C. During the experiment, the

temperatures of the dried material and the heating

agent leaving the drum were measured and are listed

in Tables 1–8. During the experiment, samples of

dried material were taken and their moisture content

was determined. The moisture content of the samples

is determined by drying them at 105°C for 3 hours in

an oven. The experiment results are shown in Figure

Hydraulic Resistance to Air Flow in Drum Dryers

781

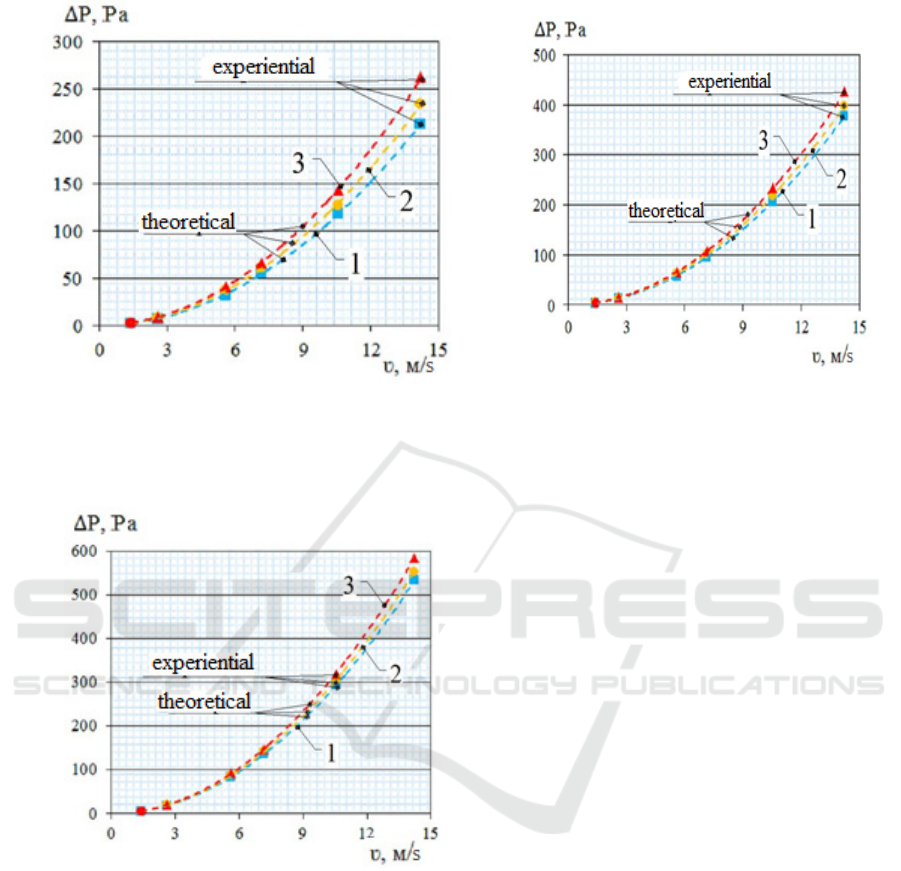
At Q = 0.02 kg /s .

Figure 3: plotted on a graph

At Q = 0.03 kg /s.

Figure 4: plotted on a graph

At Q = 0.04 kg /s.

Figure 5: plotted on a graph

1 - slope of the filling part of the nozzle R = 15

;

2 - slope of the filling part of the nozzle R = 30

;

3 - slope of the filling part of the nozzle R = 45

;

Figures 3-5: Dependence of hydraulic resistance on gas speed.

ICHELS 2024 - The International Conference on Humanities Education, Law, and Social Science

782

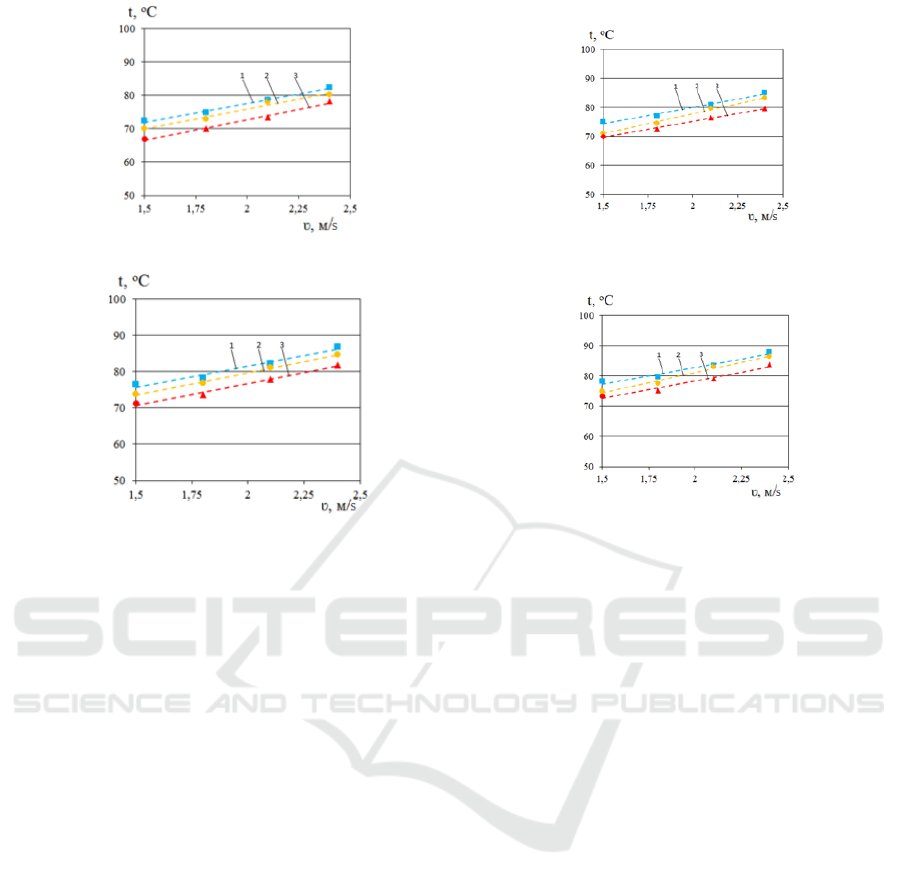
n = 2.5 rpm -const

n =3 rpm -const

n = 3.5 rpm -cons

n = 4 rpm -const

–

=0.02 k

/s; 2

–

=0.03 k

/s; 3

–

=0.04 k

/s;

Figure 6: Dependence of coolant velocity on changes in material temperature.

As can be seen from Figure 6, with drum

performance GM = 0.02; 0.03; 0.04; 0.05 kg/s,

coolant speed in the drum W = 1.5; 1.8; 2.1; 2.4 m/s

and at a drum speed of n = 2.5 rpm, the minimum

value of the temperature of the dried mineral fertilizer

was t

= 64.90 C, and the maximum value of the

temperature of the dried mineral fertilizer was t

82.40 C. At a drum speed of n = 3 rpm, the minimum

value of the temperature of the dried mineral fertilizer

was t

= 66.90 C, and the maximum value of the

temperature of the dried mineral fertilizer was t

84.30 C. At the drum speed n = 3.5 rpm, the minimum

value of the temperature of the dried mineral fertilizer

was t

= 68.70 C, and the maximum value of the

temperature of the dried mineral fertilizer was t

86.80 C.

To determine the optimal values, a mathematical

planning method was used based on multifactorial

experiments. In theoretical studies and multivariate

experiments, the second most effective factors are

dryer performance (X1), nozzle angle (X2), coolant

velocity (X3) and coolant temperature (X4), device

hydraulic resistance, product quality and energy

consumption. The cooling temperature of the

fertilizer (Y1), the granular composition of the

material (Y2) and the hydraulic resistance of the drum

(Y3) were taken as evaluation criteria for conducting

multifactor experiments.

Assuming that the influence of factors on the

evaluation criteria will completely cover a second-

degree polynomial, experiments were carried out

based on the HARTLI-4 design.

To reduce the influence of uncontrollable factors

on the evaluation criteria, the sequence of

experiments was determined using a 1/17 random

number table, and the experiments were repeated 5

times separately.

The arithmetic mean values of the experimental

results were chosen. The results of the experiments

were processed in the appropriate order, adequately

representing the evaluation criteria, were obtained

according to the program regression equations of the

HARTLI-4 program “PLANEX”, and graphs of the

dependence of the variables on the criteria were

constructed (Figures 7-8).

Then:

The cooling temperature of the fertilizer in the

device is determined by the following regression

equation,

Hydraulic Resistance to Air Flow in Drum Dryers

783

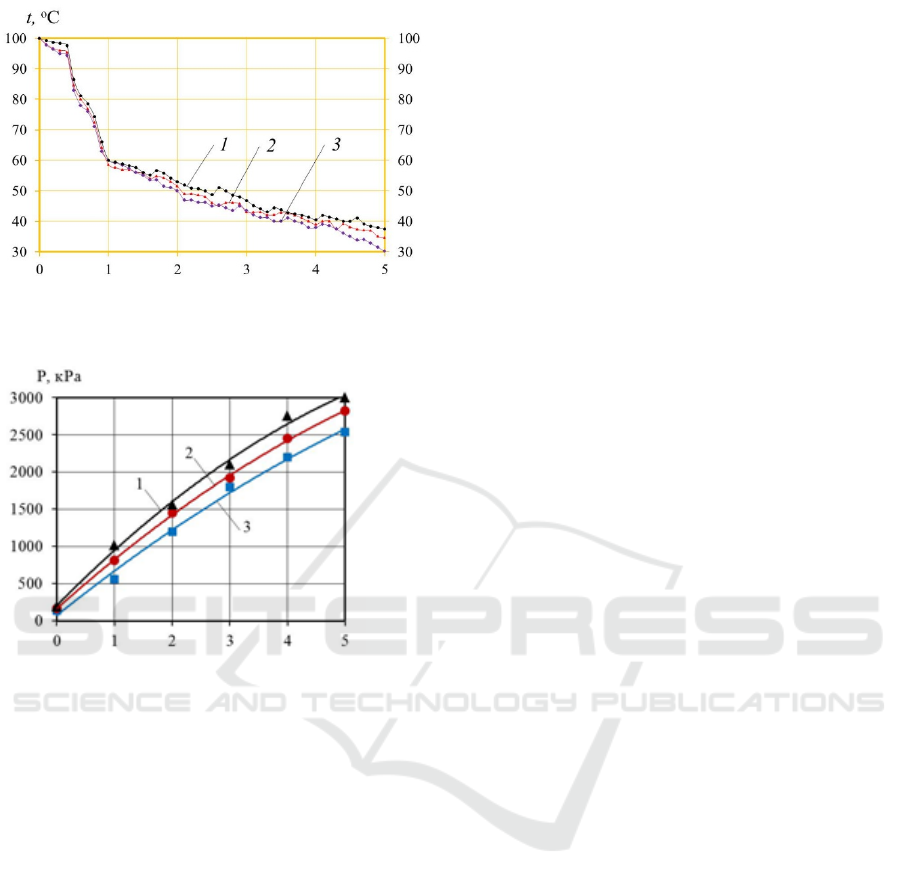
Figure 7: Dependence of fertilizer temperature on variable

factors and drum zones.

Figure 8: Dependence of hydraulic resistance on variable

factors and drum zones

= + 1 33 . 8952 + 35.563 X1 + 0.000 X2 +

154.300 X3 + 18 . 2967 X4 + 64.683 X1X1 + 45.287

X1X2 - 45.238 X1X3 - 44.679 X1X4 + 62.984

X2X2 - 22 . 7521 X2X3 - 19.629 X2X4 - 88.350

X3X3 + 45.196 X3X4 - 119.949 X4X4 ; ( 1 )

The hydraulic resistance of the drum is

determined by the following regression equation, kPa

Y = + 1329 . 121 + 3555 . 5 X1 + 3620 . 0 X2 +

1541 . 13 X3 + 1827 . 20 X4 + 2 556 . 7 X1X1 +

4520 . 2 X1X2 – 4521 . 8 X1X3 – 4457 . 8 X1X4 +

3879 . 9 X2X2 – 2274 . 50 X2X3 – 1937 . 3 X2X4 –

1 728 . 1 X3X3 + 21 17 . 0 X3X4 – 1088 . 21 X4X4

; ( 2 )

From the analysis of the obtained regression

equations (equations 1 and 2) and graphs (Figures 10-

11) it is clear that all factors have a significant impact

on the evaluation criteria. In addition, the

performance of the device, the angle of inclination of

the nozzle, the speed of the coolant and the

temperature of the coolant are in a complex

relationship with the factors under study.

4 CONCLUSIONS

To determine the factors influencing the processes

under study, the hydraulic resistance of the device,

and the optimal values of energy consumption,

regression equations were solved separately

according to specified criteria. In this case, the

fertilizer cooling temperature was taken above 30-40

C, and the hydraulic resistance of the drum was 3.4-

4 kPa. This problem was solved on a Pentium IV PC

using the Excel program “Search for Solutions”, the

optimal values of the variables were obtained in

encoded form and the encoded values were converted

into natural values. Thus, the optimal parameters for

the values of the determined criteria were

standardized and amounted to: dryer performance

(X1) - 0.39 kg/s, nozzle angle (X2) - 35.6 degrees,

coolant speed (X3) - 10.26 m/s and coolant

temperature (X4) - 50.4

REFERENCES

Akhunbaev, A. V. (1999). Methodology for Improving and

Calculating Drum Drying Units: Abstract of the

Dissertation for the Degree of Doctor of Sciences.

Shymkent.

Aleksandrova, T. N., Rasskazova, A. V., & Prokhorov, K.

V. (2012). Mining Information and Analytical Bulletin,

9, 284–289.

Gos, A. A. (2021). 83, 40–44.

Influence of the physicochemical properties of coals on the

compressibility and conditions for producing briquettes

and molded adsorbents. (Year not specified).

Dissertation, 144 pages.

Jumaboevich, T. R., & Rakhmonalievna, R. N. (2022).

Installation for Drying Materials in a Fluidized Bed.

Innovative Technologica: Methodical Research

Journal, 3(11), 28–36.

Pavlysh, V. N., Nazimko, E. I., Tarabaeva, I. V.,

Naumenko, V. G., & Perinskaya, E. V. (2013).

Mathematical Modeling of Dehydration Processes of

Enriched Mineral Raw Materials. Monograph under

the general editorship of Prof. Pavlysh V. N., Prof.

Nazimko E. I. Donetsk: "VIK".

Petrova, L. A., Latyshev, V. G., & Burenina, O. N. (2007).

Production of household fuel briquettes using

petroleum binders. Online Journal. Oil and Gas

Industry, 1–14.

Romanko, P. G., & Frolov, V. F. (1990). Mass-Transfer

Processes in Chemical Technology. Leningrad:

Chemistry.

Tang, J., Feng, H., & Shen, G. Q. (2003). Drum drying.

Encyclopedia of agricultural, food, and biological

engineering, 211-214.

ICHELS 2024 - The International Conference on Humanities Education, Law, and Social Science

784

Koraboev, E. (2022). Reliable performance and reasonable

design of drum dryer machine. Science and

innovation, 1(A7), 575-581.

Su, Y., Zhang, M., & Mujumdar, A. S. (2015). Recent

developments in smart drying technology. Drying

Technology, 33(3), 260-276.

Aghbashlo, M., Hosseinpour, S., & Mujumdar, A. S. (2015).

Application of artificial neural networks (ANNs) in

drying technology: a comprehensive review. Drying

technology, 33(12), 1397-1462.

Brammer, J. G., & Bridgwater, A. V. (1999). Drying

technologies for an integrated gasification bio-energy

plant. Renewable and sustainable energy reviews, 3(4),

243-289.

Khoshkava, V., & Kamal, M. R. (2014). Effect of drying

conditions on cellulose nanocrystal (CNC) agglomerate

porosity and dispersibility in polymer

nanocomposites. Powder Technology, 261, 288-298.

Janowicz, M., & Lenart, A. (2018). The impact of high

pressure and drying processing on internal structure and

quality of fruit. European Food Research and

Technology, 244, 1329-1340.

Le Bissonnais, Y., Bruand, A., & Jamagne, M. (1989).

Laboratory experimental study of soil crusting:

Relation between aggregate breakdown mechanisms

and crust stucture. Catena, 16(4-5), 377-392.

Sharma, L. K., Sirdesai, N. N., Sharma, K. M., & Singh, T.

N. (2018). Experimental study to examine the

independent roles of lime and cement on the

stabilization of a mountain soil: A comparative

study. Applied Clay Science, 152, 183-195.

Hydraulic Resistance to Air Flow in Drum Dryers

785