AI-Driven Lung Cancer Screening: A Comparative Analysis of

Machine Learning Models

Peilin Li

, Shirui Lyu

2* b

and Peter Niu

Aquinas International Academy, Ontario, U.S.A.

Computer Science, University of Nottingham, Nottingham, U.K.

The Erindale Academy, Mississauga, Canada

Keywords: Artificial Intelligence, Lung Cancer Prediction, Machine Learning.

Abstract: This study explores the application of artificial intelligence (AI) in the field of lung cancer screening,

evaluating the performance of three machine learning models: Random Forest, K-Nearest Neighbors (KNN),

and Decision Tree. The Random Forest model emerged as the most accurate, with an overall accuracy of

88.2% and a balanced performance across both classes, indicating its superior generalization capability for

new data subsets. Feature importance analysis revealed that 'Age' was a significant predictor in both Random

Forest and Decision Tree models, highlighting its predictive value in the dataset. The KNN model, while

achieving an accuracy of 81.6%, exhibited a performance imbalance, particularly struggling with class 0

samples, likely due to insufficient clustering or separation between classes. The Decision Tree model's lower

accuracy was attributed to potential overfitting in the training subset, capturing noise specific to the training

data and reducing its generalization ability. Notably, 'Chronic Disease' was found to be a highly important

feature in the Decision Tree model, suggesting a biased decision rule. Overall, the findings underscore the

potential of AI in enhancing lung cancer screening and the importance of feature selection and model

generalization in achieving accurate predictions.

1 INTRODUCTION

Lung cancer is one of the malignant tumors with the

highest morbidity and mortality worldwide and poses

a serious threat to human health. According to the

International Agency for Research on Cancer, the

number of new lung cancer cases worldwide is

expected to reach 2.48 million in 2022, with about

106.06 million new cases in China, accounting for

about 42.766 percent of the global total. The main

causes of lung cancer include smoking, air pollution,

occupational exposure, genetic factors, and chronic

lung disease. Smoking is considered the most

important preventable risk factor, accounting for

about 85% of all lung cancer cases. The harm of lung

cancer is not only reflected in the high mortality rate,

but also includes the significant decline in the quality

of life of patients (Minna, 2002; Tao, 2019; Wistuba,

2016). However, the traditional lung cancer diagnosis

https://orcid.org/0009-0004-7133-8444

https://orcid.org/0009-0006-0764-2921

https://orcid.org/0009-0007-5024-9516

methods mainly rely on the manual judgment of

doctors, there is a high rate of misdiagnosis and low

efficiency, especially in the early screening stage, and

the labor cost is relatively high. Therefore, there is an

urgent need to explore more efficient auxiliary

diagnosis using some advanced methods. Artificial

Intelligence (AI), as an emerging technology, has

strong feature extraction and prediction capabilities,

and can provide more accurate auxiliary support in

imaging data analysis, which can be considered in this

scenario.

Due to the development of machine learning, and

deep learning, AI has achieved great progress that

cannot be ignored, and is moving towards

diversification, refinement and precision. There are

numerous AI-based models developed, such as

random forests and neural networks. They all have the

ability to solve practical problems without exception

and play a role in some professional fields. The da

310

Li, P., Lyu, S. and Niu, P.

AI-Driven Lung Cancer Screening: A Comparative Analysis of Machine Learning Models.

DOI: 10.5220/0013329700004558

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Modern Logistics and Supply Chain Management (MLSCM 2024), pages 310-314

ISBN: 978-989-758-738-2

Vinci surgical robot developed by Intuitive Surgical

in the United States is a good example. It can already

perform cardiothoracic surgery, gynecology and

general surgery. AI is also used in the prediction of

diseases and epidemics. For instance, during the

covid-19 epidemic, China's Alibaba Damo Academy

developed an AI-driven epidemic prediction model.

This model predicts the development trend of the

epidemic by analyzing real-time data, helping

governments and health organizations to formulate

response strategies; Google's DeepMind has

developed a predictive AI called the AlphaFold

project and successfully predicted the protein

structure related to SARS-CoV-2 (the virus that

causes COVID-19). This achievement helps scientists

understand the biological characteristics of the virus

more quickly and accelerates the development of

vaccines and drugs. In terms of personalized

medicine, the AI model developed by Illumina has

done an excellent job. It accelerates the analysis of

DNA sequencing data and helps identify genetic

variants that cause diseases. Through AI, scientists

can discover the association between specific genes

and specific diseases or characteristics to help predict

disease risks. However, it can be found that most

widely used AI models are basically considering

independent and identically distributed situations,

and there are few in-depth studies on the versatility

and compatibility of the models, that is, different

distribution predictions. So this study aims to develop

the model in this research direction for evaluating the

applicability of machine learning models.

In this study, we used a dataset from Kaggle. The

dataset was preprocessed to remove missing values

and normalize the features. In order to explore model

performance with different data distributions, the K-

means clustering algorithm (K=2) was applied to

divide the dataset into two distinct subsets. These

subsets were labeled as A and B and further saved as

separate CSV files for latter analysis. We trained

three machine learning models — Decision Tree,

Random Forest, and K-Nearest Neighbors (KNN)—on

subset A. Model training procedures including

hyperparameter tuning using a grid search approach

and cross-validation were aimed to optimize

performance. To evaluate model generalization, the

trained models were directly tested on subset B. We

assessed model performance by comparing results

across the different algorithms with accuracy, F1-

score, and ROC-AUC metrics.

2 METHOD

2.1 Dataset Preparation

In this study, we used a dataset from Kaggle,

including 15 features and 1 target variable. The

dataset was preprocessed to remove missing values

and normalize the features. In order to explore model

performance with different data distributions, the K-

means clustering algorithm (K=2) was applied to

divide the dataset into two distinct subsets. These

subsets were labeled as A and B and further saved as

separate CSV files for latter analysis.

2.2 Machine Learning Models

2.2.1 Decision Tree and Random Forest

A decision tree is a popular data mining technique

used for both classification and regression tasks

(Song, 2015; Suthaharan, 2016; Su, 2006). It is

structured like a tree where each internal node

represents a test on an attribute, each branch

represents the outcome of that test, and each leaf node

represents a class label (in classification) or a

continuous value (in regression). Decision trees work

by breaking down a complex decision-making

process into a series of simpler decisions, making it

both easy to follow and interpret.

Random forests introduce randomness and

diversity in multiple ways to build robust predictive

models (Rigatti, 2017; Biau, 2016; Belgiu, 2016).

Firstly, data randomness is employed during the

construction of each decision tree; the algorithm

randomly extracts samples from the training dataset

with replacement, a technique known as Bootstrap,

ensuring each tree uses a different subset of data.

Additionally, feature randomness is applied in the

node splitting process where not all features are

considered; instead, a random subset is selected for

the best split, preventing any single feature from

dominating the trees. Each decision tree is

constructed independently, using different data and

selected features, which may lead to varying

prediction outcomes across trees. In the final

prediction stage, random forests utilize voting for

classification tasks—making a majority decision

based on the predictions from all trees—and

averaging for regression tasks, where the final

prediction value is calculated by averaging the

outputs of all decision trees. This methodology

enhances the model's accuracy and generalizability

by mitigating overfitting and ensuring a diverse set of

predictions.

Random forests have several advantages: 1) Anti-

overfitting: Since each forests tree is built based on a

AI-Driven Lung Cancer Screening: A Comparative Analysis of Machine Learning Models

311

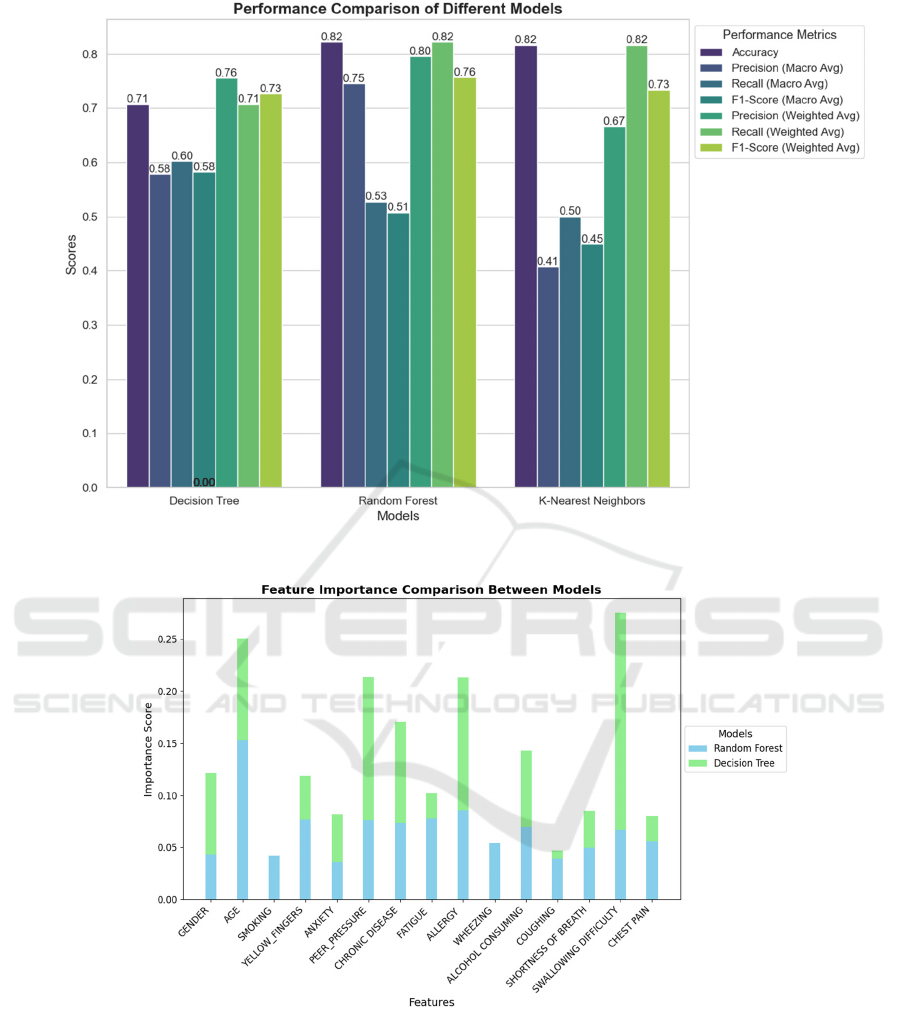
Figure 1: The performance of various models (Photo/Picture credit: Original).

Figure 2: The feature importance of various models (Photo/Picture credit: Original).

different random subset, it is less prone to overfitting

than a single decision tree 2) Strong stability:

Random forests are insensitive to noise and outliers

in the data because it is the result of voting or

averaging multiple trees 3) Strong ability to handle

high-dimensional data: Random forests can

effectively handle data sets with a large number of

features 4) Feature importance evaluation: Random

forests can evaluate the importance of each feature to

the model's prediction results and help understand the

key features in the data

2.2.2 KNN

KNN is a supervised learning algorithm widely used

for classification and regression tasks (Guo, 2003).

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management

312

KNN uses distance metrics to classify or predict new

samples based on the assumption that "similar objects

have similar outputs." How the KNN algorithm works

Select the K value: K represents the number of

neighbors, that is, the K neighbors closest to the test

sample are considered when predicting. The process

of it includes multiple steps: 1) Calculate the distance:

For a given test sample, calculate its distance from

each sample in the training set. Commonly used

distance metrics include Euclidean distance,

Manhattan distance, cosine similarity, etc. 2) Select

the nearest K neighbors: Sort the samples in the

training set according to the distance, and select the K

nearest to the test sample. Neighbor. 3) Classification

or regression: Classification task: According to the

categories in the K nearest neighbors, the

classification of the test sample is determined by a

voting mechanism. In other words, the category with

the most occurrences is the predicted category of the

test sample. 4) Regression task: According to the K

nearest neighbors the value is usually taken as the

average value as the prediction result of the test

sample.

KNN has several advantages: 1) Simple and easy

to understand: KNN is one of the simplest machine

learning algorithms, easy to understand and

implement, and does not require a complex model

training process. 2) Parameter-free model: KNN is a

non-parametric algorithm that does not perform

explicit model fitting on the data. It is suitable for data

sets with unknown or complex data distribution 3)

Suitable for small data sets: KNN performs well for

small data sets or when there are not many features

and can effectively classify or regression 4) Can

handle multi-category problems: KNN can be

naturally extended to multi-classification problems

(i.e. not limited to binary classification), and only

needs to select the nearest K samples for voting.

3 RESULTS AND DISCUSSION

The performance of the three ML models was

evaluated using metrics including accuracy, macro-

averaged and weighted-averaged precision, recall,

and F1-Score, as comprehensively presented in

Figure 1. Figure 2, on the other hand, shows the

importance scores of each feature in the decision tree

and random forest models.

The Decision Tree model demonstrated an

accuracy of 70.7%. The macro-averaged precision,

recall, and F1 score were 0.58, 0.60, and 0.58,

respectively. The weighted average precision, recall,

and F1 score were 0.76, 0.71, and 0.73, respectively.

Age and Chronic Disease were identified as the most

impactful features, with importance scores of 40.3%

and 23.5%, respectively.

The Random Forest model achieved the highest

accuracy of 82.1%, with macro-averaged precision,

recall, and F1 scores of 0.75, 0.53, and 0.51,

respectively. The weighted average precision, recall,

and F1 scores were 0.80, 0.82, and 0.76, respectively.

Age and Alcohol Consumption emerged as the most

significant features, contributing 38.6% and 13.4% to

the model's predictions, respectively.

Meanwhile, the KNN model attained an accuracy

of 81.6%. Its macro-averaged precision and recall

were 0.41 and 0.50, respectively, with a macro-

averaged F1 score of 0.45. The weighted average

precision, recall, and F1 scores were 0.67, 0.82, and

0.73, respectively. However, this model exhibited a

notable performance imbalance, with a precision of

0.00 for class 0, suggesting difficulty in correctly

identifying samples from this class.

Among the three models, the Random Forest

demonstrated the highest overall accuracy and

balanced performance across both classes, suggesting

better generalization to new data subset. This

performance may be attributed to the ensemble

learning the nature of Random Forest, which

effectively reduces variance and overfitting. In

contrast, the KNN model's zero feature importance is

anticipated, as it is a distance-based algorithm that

does not have the ability to inherently assign weights

to features during training. Its difficulty in

recognizing class 0 is probably due to the lack of

significant clustering or separation between class

samples. The lower accuracy of the Decision Tree

model may be due to overfitting in the training subset

A. The model captures excessive noise specific in the

training data, thereby reducing its ability to generalize

to unseen data in subset B. Feature importance

analysis indicates that 'Age' is consistently a

significant predictor in both the Random Forest and

Decision Tree models, underscoring its strong

predictive value within this dataset. In contrast,

'Chronic Disease' demonstrated a substantially higher

importance in the Decision Tree model, which may

suggest the presence of a biased decision rule heavily

reliant on this specific feature.

4 CONCLUSIONS

Overall, this study employed a clustering approach to

explore the generalizability of different models in

predicting lung cancer by training the models on one

subset and testing them on the other. We utilised the

K-means algorithm for clustering the original dataset

AI-Driven Lung Cancer Screening: A Comparative Analysis of Machine Learning Models

313

and trained three common machine learning models —

Decision Trees, Random Forests, and the K-Nearest

Neighbors (KNN) — on subset A. In summary, the

Random Forest and the KNN models demonstrate

superior performance in terms of accuracy. However,

the Random Forest model proves more robust in

handling category imbalance, while the KNN model

performs relatively poorly on macro-averaged

metrics. The Decision Tree model, despite its lower

overall accuracy, shows strength in balancing

category performance. These findings suggest that

while Random Forests are a robust choice for datasets

with imbalanced categories, KNN and Decision Trees

may have specific advantages depending on the

performance metrics prioritized. Future studies could

explore advanced techniques such as transfer learning

and domain adaptation to improve model

generalizability across diverse datasets and clinical

settings.

AUTHORS CONTRIBUTION

All the authors contributed equally, and their names

were listed in alphabetical order.

REFERENCES

Belgiu, M., & Drăguţ, L. 2016. Random forest in remote

sensing: A review of applications and future

directions. ISPRS journal of photogrammetry and

remote sensing, 114, 24-31.

Biau, G., & Scornet, E. 2016. A random forest guided

tour. Test, 25, 197-227.

Guo, G., Wang, H., Bell, D., Bi, Y., & Greer, K. 2003. KNN

model-based approach in classification. In On The

Move to Meaningful Internet Systems 2003: CoopIS,

DOA, and ODBASE: OTM Confederated International

Conferences, CoopIS, DOA, and ODBASE 2003,

Catania, Sicily, Italy, November 3-7, 2003.

Proceedings (pp. 986-996). Springer Berlin Heidelberg.

Minna, J. D., Roth, J. A., & Gazdar, A. F. 2002. Focus on

lung cancer. Cancer cell, 1(1), 49-52.

Rigatti, S. J. 2017. Random forest. Journal of Insurance

Medicine, 47(1), 31-39.

Song, Y. Y., & Ying, L. U. 2015. Decision tree methods:

applications for classification and prediction. Shanghai

archives of psychiatry, 27(2), 130.

Suthaharan, S., & Suthaharan, S. 2016. Decision tree

learning. Machine Learning Models and Algorithms for

Big Data Classification: Thinking with Examples for

Effective Learning, 237-269.

Su, J., & Zhang, H. 2006. A fast decision tree learning

algorithm. In Aaai (Vol. 6, pp. 500-505).

Tao, M. H. 2019. Epidemiology of lung cancer. Lung

Cancer and Imaging, 4-1.

Wistuba, I. I., & Gazdar, A. F. 2006. Lung cancer

preneoplasia. Annu. Rev. Pathol. Mech. Dis., 1(1), 331-

348.

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management

314