Holiday Effects on S&P 500 Index Volatility and Return Rates for

Market Efficiency Validation

Zihan Li

School of ACCOUNTING& FINANCE, Hong Kong Polytechnic University, Hong Kong, China

Keywords: Holiday Effect, Market Effectiveness, GARCH.

Abstract: The holiday effect in the financial landscape is important, especially in understanding how market behaviour

changes around holidays. This phenomenon has been under-appreciated in the past. This article provides

additional evidence for the holiday effect. It analyses whether the volatility and returns in the S&P 500 Index

are significantly different between the five trading days before the holiday, and the rest period. Next, the

effectiveness of the market is determined through the 'efficient market hypothesis'. The adjusted closing price

for the S&P 500 index was calculated for each trading day between December 23, 2013 and December 29,

2023. This work will build a Generalized Autoregressive Conditions Heteroskedasticity model (GARCH) to

calculate the volatility of the index through the index returns. Both datasets are tested using the F Test method

and T Test method. The results show low volatility and high returns for the five-trading day of the pre-holiday

time period. As a result, it indicates that the holiday effect is predominant in S&P 500 Index, which represents

by the 500 U.S. companies that are under the control of the S&P 500. Due to arbitrage opportunities, the U.S.

Stock Market has low efficiency.

1 INTRODUCTION

In financial market analysis, the "holiday effects"

refers to an anomaly in the market (Gama, 2013;

Brockman, 1998), a pattern of unusual volatility and

returns on the stock market, which often occurs just

before a holiday. The stock market performs better

than usual in the days leading up to holidays, and

rising prices of stocks imply high returns. This

suggests that stock returns before holidays are

different from other time periods. Short-term returns

are usually higher before holidays, which is contrary

to the efficient market hypothesis. According to the

EMH, stock prices already contain all available

information, so investors cannot outperform the

market. The data was selected for each trading day

from December 23, 2013, to December 29, 2023. This

work will build a Generalized Autoregressive

Conditions Heteroskedasticity model (GARCH) to

calculate the volatility of the index through the index

returns. Both datasets are tested using the F-Test

method and T-Test method. The results show low

volatility and high returns for the five-trading day of

the pre-holiday time period. These results indicate

that the holiday effect is predominant in U.S. Stock

Market, which represents by S&P 500 Index. Due to

arbitrage opportunities, the U.S. Stock Market has

low efficiency.

In other words, no investor can make exceed

profit in an efficient market. This makes sense to a

large extent, but everything has two sides. The

discovery of the holiday effect challenged EMH by

suggesting that the behavior of market participants

could be influenced by irrational factors such as

investor sentiment or behavioral biases. Such unusual

stock performances have attracted the interest of

many financial analysts and market participants

because they allow investors to earn additional

returns on both short-term and long-term trades. Such

unusual phenomenon is represented by several

markets around the whole world and it is worth

exploring whether such phenomenon could have a big

impact on major stock indices like S&P 500. Because

the U.S. stock market is representative of global

equity markets. Investigating the influence of the

holiday effect on the S&P 500 and analyzing in depth

its role on volatility and returns will greatly assist the

understanding of market anomalies in the U.S. stock

market. Examining the holiday effect not only

challenges traditional financial theories, but also

provides insight into the correlation between the S&P

500 and related financial contracts through data

Li, Z.

Holiday Effects on S&P 500 Index Volatility and Return Rates for Market Efﬁciency Validation.

DOI: 10.5220/0013270300004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 547-552

ISBN: 978-989-758-726-9

547

comparisons that reveal the efficiency of the U.S.

market as a whole.

Market volatility and returns are widely

recognized as important indicators of economic

performance and the investment performance of the

global financial system. Volatility refers to the

magnitude and speed of change in asset prices over

time. High-volatility financial products experience

significant price changes, reflecting the

unpredictability and instability of markets, while low-

volatility financial instruments are relatively stable.

The performance of the Standard & Poor's 500 Index

(S&P 500) is closely related to the volatility of the

stock market, especially in the United States (Ang,

Hodrick, Xing, & Zhang, 2006). Therefore, its

performance can serve as a reliable indicator of

market volatility in the United States. In addition, the

S&P 500 index represents 500 of the largest and best-

known publicly traded companies in the United

States, covering different industries such as energy,

consumer goods, and technology, reflecting the

market capitalization performance of these industries

and thus the overall performance of the U.S.

economy. As a result, changes in the index can also

reflect the overall economic conditions in the United

States. In order to effectively explore the anomalies

of the U.S. market and help financial market

participants manage risks and formulate investment

strategies; the selection of the S&P 500 Index is

reasonable. In addition, volatility and yield, as

important parameters for assessing investment

performance, are sensitive to changes in market

efficiency. Studying how they are affected, and their

intrinsic relationship can make important predictions

about market trends and help financial institutions

and individual investors make informed decisions.

Since this study more focus on analyzing in depth

whether holiday effects exist. This essay will provide

a comprehensive understanding of U.S. stock market.

It will also examine whether they have an effect on

S&P500 volatility and returns. A detailed analysis of

this holiday effect will help market participants, risk

managers and traders to better understand the market

and optimize their trading and risk management

strategies. it will also provide richer insights on

patterns of market behavior in periods of unusual

volatility. This will be useful for understanding and

predicting future market direction. The article

predicts that the S&P 500 will show a holiday effect

in the follow-up experiments. This manifests as lower

volatility, higher returns and higher risks during

holiday periods.

2 LITERATURE REVIEW

2.1 Holiday Effect Verification

The EMH theory is one of the cornerstones in

financial economics. This theory assumes market

prices reflect all information available, thus rejecting

the possibility that speculators could exploit

information to generate excess returns (Fama, 1970).

The EMH theory has been widely accepted by

professional financial practitioner as applicable to the

financial markets. However, there are persistent

anomalies that have been observed in actual markets

which challenge this theory. Investors may notice

anomalies when they look at data and see that a stock

has outperformed the market over time in a particular

characteristic. One such anomaly is the holiday effect.

Before delving into the volatility and returns of the

S&P 500 over time, it's important to first determine if

the holiday effect exists.

Lakonishok & Smidt (Lakonishok, 1988), in order

to explore market anomalies and test for persistent

seasonal patterns, conducted pioneering research to

test for 90 years of U.S. closing price data for Dow

Jones Industrial Average. Lakonishok & Smidt

(Lakonishok, 1988), by analysing the data collected,

pointed out that there were persistent and abnormally

higher returns around certain times, such as

weekends, the end of the month, the end of the year,

and holidays. Stock returns are significantly higher at

these times than they are on normal trading days,

which indicates that there may be systematic

anomalies in this market. The holiday effect was

brought into focus by the challenge to traditional

market models.

Kim and Park (Kim, 1994), comparing data from

July 1, 1973, to June 30 1987, explore the holiday

effect on stock returns. They found that stocks on the

three major U.S. stock exchanges (the New York

Stock Exchange, the American Stock Exchange, and

the NASDAQ) had unusually high returns in the days

leading up to the holidays. The study also verified the

holiday effect in the UK and Japanese stock markets.

The results show that the holiday effect in the UK and

Japanese markets is independent of the US market,

and that this phenomenon persists even after taking

into account the impact of the US holiday effect. This

indicates that there is an international linkage to the

holiday effect. By comparing stock returns between

the holiday season and the next, it was confirmed that

all 14 CEE financial market had abnormally high

stock return (Gakhovich, 2011). The holiday effect is

also present in this case. The holiday effect is

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

548

confirmed in multiple locations as Lakonishok &

Smidt's findings have been verified.

The holiday effect on the Swedish stock market is

missing, according to Eidinejad & Dahlem's

(Eidinejad, 2021) analysis of daily price data for the

Swiss stock exchange over a 40-year period between

1980-2019. Their results show a significant post-

holiday effect in the Swedish Stock Market over the

entire sample time period. This is evidenced by

significantly higher stock market returns than other

times. This is not the same as the holiday effect,

which indicates abnormally volatile returns before the

holidays. When the sample was broken down by

decade, researchers found that the holiday effects

were primarily present in the 1990s & 2000s. The

effect was not seen in the 1980s & 2010s. The study

also found no pre-holiday effects in any period. The

article explains why this phenomenon occurs. The

rapid development of Internet in 1990s may well have

caused investors to pay more attention to the market

during holidays. This may have been a reason for the

post-holiday effects in 1990s. By 2010, the market

might have adjusted to this anomaly. The findings of

the Swedish stock exchange support the idea that

holiday effects are not always present on the market.

2.2 S&P 500 Volatility Effect

Financial market analysis is not complete without

understanding the impact of market volatility on

investment returns. The traditional view of

investment emphasizes that low-volatility stocks on

the market are typically associated with less price

fluctuation and may therefore represent lower risk

and lower return. This intuitive concept implies

higher risk is required for investors to achieve higher

returns.

A leading academic quarterly in finance called

The Journal of Portfolio Management published an

article that suggests a different view. Blitz & Van

Vliet (Blitz, 2007) created quartile portfolios based

upon historical volatility, and compared performance

of different volatility-based portfolios using stock

market data from 1986 to 2006. Their research

revealed that low volatility portfolios are not only

associated with lower risks, but also have higher

adjusted returns than high volatility portfolios. It is

important that they also analyzed portfolios from

other markets. This phenomenon is not limited to one

market but is present in many markets around the

world, including the U.S.A., Europe, China and

Japan. To verify that this phenomenon was not a

fortuitous circumstance, the article also explored

whether other factors, such as size, value, or

momentum, which are known to have financial

market effects, could have an effect on this low-risk,

but high return, compared to the return of a portfolio

with low volatility. The results show that the low

volatility is still significant after controlling for all of

these factors. This indicates that it is a separate and

economically significant effect. This unusual

phenomenon brings up an important point: in certain

situations, the traditional association between equity

market volatility and risk may need to be reevaluated.

The article provides new perspectives on practical

risk management and asset allocation.

In this context, it is important to analyze changes

in volatility and returns for the S&P 500, under the

influence of holiday effects. The performance of S&P

500 can be a good indicator of the state of the U.S.

stock market. Its performance during a certain time

period such as pre-holidays, for example, can give

investors important information to make investment

decisions. A more detailed analysis of the S&P 500's

risk and reward patterns can reveal the nuances in

market dynamics when influenced by specific

holidays. This can help investors to not only

capitalize on trading opportunities over the short-

term, but also give them insight into long-term

investment strategy development.

3 METHODOLOGIES

3.1 Data Preparation

In contemporary era background, the stock market

provides a fair, transparent and cost-effective

environment for the investors to make investment on

nearly equal condition to foster the healthy

development of economic. investors can easily search

lots of stock information from some financial website

such as wind, yahoo finance and Bloomberg. This

article chooses the yahoo finance as data resource.

Because this website can be used by public investors

to find stock price. Therefore, this article used the

adjust closed price of S&P 500.

S&P 500 Index Adj Close: This dataset represents

the closing price of a stock at the end of a given

trading day, after taking into account factors such as

ex-rights and dividends. Its price reflects the true

value of the stock. Historical data from 2013-12-23 to

2023-12-29 is included here.

In addition, the calculation of index return rate is

the key factor of this research. The volatility this

article discuss is also generated from the return rate.

Holiday Effects on S&P 500 Index Volatility and Return Rates for Market Efﬁciency Validation

549

It is essence to use precise quantitative date for the

calculation of return rate of S&P 500.

3.2 Model Construction

Since volatility is not directly observable, this paper

requires a reliable proxy variable. If the conditional

mean is zero, the square of the returns can be used as

an unbiased estimate of the underlying volatility

process. (Awartani, 2005). Therefore, creating the

Specialized models to make prediction by using

return rate is the key factor of this experiment.

At the beginning of the experiment, this article

wanted to depend on the Autoregressive Conditional

Heteroskedasticity (ARCH) which can be used to

catching volatility characteristics in financial time

series data. However, Zhang (Zhang, 2016)

mentioned that this model needs the high amount of

data which can lead to a great number of problems in

the process of calculate the volatility. For instance,

the problem of multicollinearity of the explanatory

variables and the inability to ensure that the

restriction α is always not less than zero.

Therefore, this article chose the GARCH model

(Xu, 2011) to calculate the volatility. Because this

model can easily find heteroskedasticity, which

suggest that the volatility of the index rate is not

always constant in time series. It always changes over

the time. In addition, the basic factor of the GARCH

model is predicting the future volatility by using the

past volatility.

3.3 Test Method

Since this article must judge the significant difference

between two data set, this article will use some test to

help determined. the F Test and T Test is the best

option to make judgement.

3.3.1 F Test

For the F test, it usually is used to compare whether

the variances were significantly different between

two or more samples.

The basic set of steps is to ensure the null

hypothesis H0: The variance of two samples is equal;

alternative hypothesis Ha: The variance of two

samples is not equal.

The formulas are shown below:

𝑆







∑

𝑛



𝑥



𝑥^2





𝑘1

⁄

(1)

𝑆







∑

𝑛



𝑛



 1𝑆







𝑁𝑘1

⁄

(2)

Throughout the experiments, this work decided to

use the EXCEL to help simplify the process of

calculating the F statistic.

Finally, this article will determine the

corresponding p value based on the F statistic. The

acceptance of the original hypothesis will be

determined by the comparing the p value to the

magnitude of 0.05.

3.3.2 T Test

T-tests are commonly used to determine whether the

means of two or more samples are significantly

different. The basic steps include setting the null

hypothesis H0: The means of two samples are equal;

alternative hypothesis Ha: The means of the two

samples are not equal. If the p-value is less than 0.025,

the null hypothesis is rejected.

4 RESULTS AND DISCUSSION

4.1 Calculate The S&P 500 Volatility

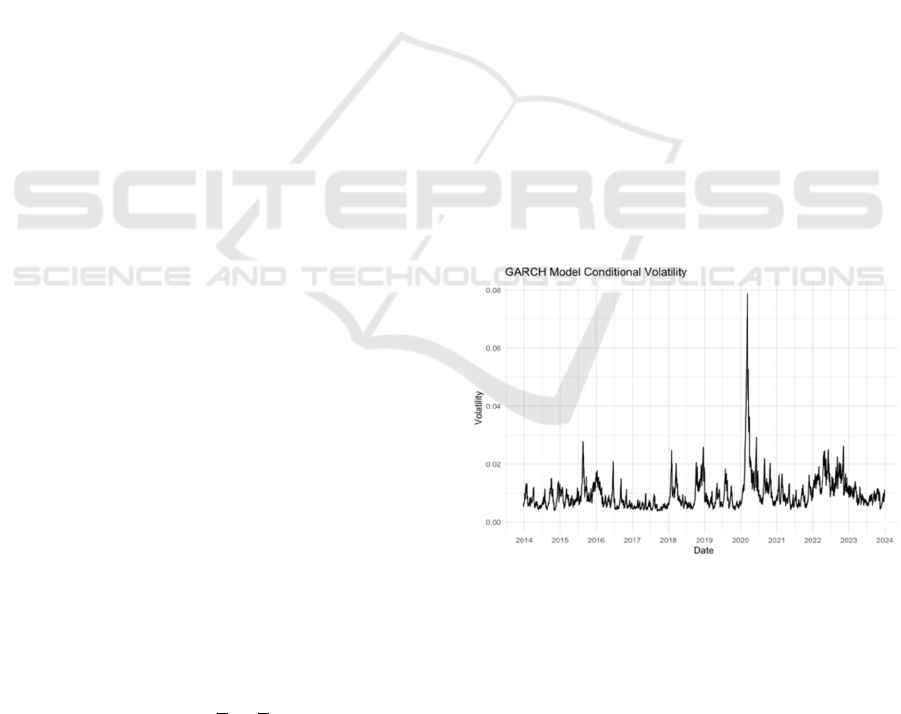
For the validation of the existence of the holiday

effect. this article first wanted to use the average daily

volatility of the S&P 500 based on all of the 2013 to

2023 period shown in Figure 1 to see if there were any

unusual fluctuations in it. This essay imported the

data in to RStudio and obtained the GRACH model

diagram shown in the figure after code programming.

Figure 1: 10 Years Index Volatility (Photo/Picture credit:

Original).

4.2 Return Rate Calculation

"The most widely-used statistics in finance are

expected return and volatility" (Sakr & Sherif, 2017).

The calculation of volatility is derived from the

returns. Therefore, this study calculated the returns

first. This article can easily calculate the daily returns

by using a formula on an EXCEL sheet. The formula

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

550

is the ratio of adjusted closing prices of the current

trade, minus the adjusted close of the previous day's

trading, to the adjusted close of the previous day's

trading. The same formula can be used to calculate

daily returns after obtaining the daily returns of Index

and Futures over the ten-year period.

4.3 F Test

Excel software is used to calculate the F statistics,

with significance set at 95%, corresponding to a p-

value of 0.05. If the p-value is below 0.05, the null

hypothesis is rejected, indicating a significant

variance difference between the two groups.

4.3.1 S&P 500 Return Rates

The null hypothesis for this F test is the following: the

variance in return rates of the S&P 500 index in the

pre-holiday periods equals the variance in return rates

of the index in the non-holiday periods.

The alternative hypothesis is that the variances of

the S&P 500 return rate in pre-holiday periods are not

equal to the variances of the index return rates during

non-holiday periods.

H0: b1=b2 (3)

Ha: b1≠b2 (4)

The graph below shows that the F statistic is

1.37493. This means that the p-value is 1.74E-04

which is less than 0.05

There is strong evidence that this article rejects the

null hypotheses and accept the alternative hypotheses.

proving a significant difference in the variances of the

S&P 500 Index return rates between pre-holiday and

non-holiday periods.

4.3.2 S&P 500 Volatility

The null hypothesis for this F test is the following:

the variance in Volatility of the S&P 500 index in

the pre-holiday periods equals the variance in

Volatility of the index in the non-holiday periods.

The alternative hypothesis is that the variances of

the S&P 500 Volatility in pre-holiday periods are

not equal to the variances of the index Volatility

during non-holiday periods.

H0: b3=b4 (5)

Ha: b3≠b4 (6)

The graph below shows that the F statistic is

2.24308. This means that the p-value is 1.05E-23

which is less than 0.05

There is strong evidence that this article should

reject the null hypotheses and accept the alternative

hypotheses. This proves that there is a significant

difference between the variances of the S&P 500

Index Volatility during Pre-holiday and the variances

of the index Volatility during the non-holiday

periods.

4.4 T Test

The F Test shows that both return rates and

volatility are significantly different between the

holiday period and the non-holiday periods. This

article chose the T test for two sample

heteroskedasticity. Then, this essay will calculate

the confidence intervals of both and determine if

there is a significant difference in the mean.

4.4.1 The T Test about S&P 500 Return

Rates

The null hypothesis for this t-test is that the index

returns rates during non-holiday times are equal to the

S&P 500' return rates in pre-holiday times. The

alternative hypothesis is the S&P 500' return rate in

the pre-holiday period does not equal that of the index

during the non-holiday period.

H0: m1=m2 (7)

Ha: m1≠m2 (8)

Since this article set the significance at 95% it

means that a=0.05. When p value (single tailed

critical mass), is less than a/2 =0.025the null

hypotheses was rejected. In this test, p value (single

tailed critical mass), is 0.008292. This is less than

0.025. there is strong evidence for rejecting the null

hypothesis, and it can be concluded that there are

significant differences between those two types of

mean.

This article established a confidence interval by

the information which is gathered from the internet.

This article put the follow formula about confidence

interval into RStudio

(m1-m2) ± 1.96 * (σ / sqrt(n)) (9)

In the end, this article gets the 95% confidence

interval for m1-m2 which is between（-0.009473，-

0.008196359）

It represents that there is a 95% probability that

any S&P 500 return rate from non-holiday period

minus any S&P 500 return rate from pre-holiday will

be within this interval. Overall, the SP500 return rate

from the non-holiday period is less than the SP500

return rate from pre-holiday.

Holiday Effects on S&P 500 Index Volatility and Return Rates for Market Efﬁciency Validation

551

4.4.2 The T Test about S&P 500 Volatility

This t test's null hypotheses H0 are that the index

volatility in non-holiday times is equal to the

S&P500's mean volatility before holidays. The

alternative hypothesis Ha is the S&P 500's mean

volatility in the pre-holiday period does not equal

that of the index during the non-holiday period.

H0: m3=m4 (10)

Ha: m3≠m2 (11)

Since this article set the significance at 95% as its

regulation, it means that a=0.05. When p value (single

tailed critical mass), is less than a/2 =0.025, the null

hypotheses was rejected. In this test, p value (single

tailed critical mass), is 0.003443. This is less than

0.025. there is strong evidence for rejecting the null

hypothesis, and it can be concluded that there are

significant differences between those two types of

mean.

This article established a confidence interval by

the information which is gathered from internet. This

essay put the follow formula about confidence

interval into RStudio

(m3-m4) ± 1.96 * (σ / sqrt(n)) (12)

In the end, the 95% confidence interval can be

obtained for m3-m4 which is between 0.0002820763

and 0.0012361062.

It represents that there is a 95% probability that

any S&P 500 volatility from non-holiday period

minus any S&P 500 volatility from pre-holiday will

be within this interval. Overall, the SP500 volatility

from the non-holiday period is higher than the SP500

volatility from pre-holiday. This is consistent with the

domain knowledge about the index holiday effect.

5 CONCLUSIONS

This article analyzes whether the holiday effects

exist in the S&P 500. It also verifies the validity of

the market. This analysis is used both to determine if

the holiday effect has an impact on the stock market,

and to verify its validity. This analysis gives investors

food for thought as they decide on trading strategies

and risk-management strategies. This study used a

variety of data analysis techniques throughout the

paper, including the GRACH model and T-Test. The

GRACH models have been applied to more than 5000

data sets. The predictions are largely confirmed by

this research.

The model which is used in this article allowed to

calculate volatility of the S&P 500 based on its

returns. It verified the holiday effect by

experimenting with the volatility and returns of S&P

500. This article analyzed the holiday effect using

data analysis concluded that it manifests itself as

lower holiday volatility. This is contrary to what this

paper initially predicted. The expectations are higher

returns and lower volatility. This study can provide a

better option for the risk-averse investor who wants

to trade stocks. There are also some limitations. For

instance, this article successfully verified the

existence of holiday effect by studying the return rate

and volatility of sp500 index. However, it ignores

studying the components. In addition to that, this

article cannot make definition about which vacation

day is most affected by the holiday effect, which

make the analysis of the impact of holiday effect is

not precise as expected. This research hope to adopt a

more comprehensive approach to analysis in the

future to assist investors choose the best investments

strategy.

REFERENCES

Awartani, B. M. A., & Corradi, V. 2005. Predicting the

volatility of the S&P-500 stock index via GARCH

models: the role of asymmetries. International Journal

of Forecasting, 21(1), 167–183.

Blitz, D., & Van Vliet, P. 2007. The volatility effect: Lower

risk without lower return. Journal of portfolio

management, 102-113.

Bollerslev, T., Engle, R. F., & Nelson, D. B. 1994. ARCH

models. Handbook of econometrics, 4, 2959-3038.

Brockman, P., & Michayluk, D. 1998. The persistent

holiday effect: Additional evidence. Applied

Economics Letters, 5(4), 205-209.

Eidinejad, S., & Dahlem, E. 2021. The existence and

historical development of the holiday effect on the

Swedish stock market. Applied Economics Letters,

29(19), 1855–1858.

Fama, E. F. 1970. Efficient Capital Markets: A review of

theory and Empirical work. the Journal of Finance/the

Journal of Finance, 25(2), 383.

Gama, P. M., & Vieira, E. F. 2013. Another look at the

holiday effect. Applied Financial Economics, 23(20),

1623-1633.

Kim, C., & Park, J. 1994. Holiday effects and stock returns:

Further evidence. Journal of Financial and Quantitative

Analysis, 29(1), 145.

Lakonishok, J., & Smidt, S. 1988. Are seasonal anomalies

real? A Ninety-Year perspective. Review of Financial

Studies/the Review of Financial Studies, 1(4), 403–425.

Xu, J., Zhang, Z., Zhao, L., & Ai, D. 2011. The application

review of GARCH model. International Conference on

Multimedia Technology.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

552