Sales Forecasting in Retail Supply Chain Management

Junkai Zhao

School of Economics and Management, Beihang University, Beijing, China

Keywords: Sales Forecasting, Polynomial Regression, Random Forest, Retail Analytics, Feature Importance Analysis.

Abstract: In the actual production environment, the forecast of demand or sales volume is extremely important, accurate

prediction can not only effectively reduce inventory costs, but also greatly reduce production and

manufacturing costs, reduce unnecessary waste, not only that, in management, people find that the oxtail

effect will have a great impact on the stability of the supply chain, and the prediction of sales volume can

effectively reduce the negative impact of the effect, this study will take Wal-Mart's real sales volume dataset

as an example, Comparing the performance of Polynomial Regression and Random Forest (RF) in the face of

sales volume datasets, including the accuracy of prediction and generalization ability, and finding the factors

that have the greatest impact on sales volume from many objective factors affecting sales volume in the

construction process of the model, these experimental results will have important practical significance for

inventory management and resource allocation.

1 INTRODUCTION

In the retail industry, sales volume forecasting has a

very important impact on the decision-making of

retail enterprises, especially in the current

environment of lean management in the retail

industry and other manufacturing enterprises,

enterprises need to meet customer needs while

minimizing costs or maximizing benefits, and in retail

and manufacturing, inventory costs and other costs in

the supply chain account for a large part of the total

cost (Koumanakos, 2008), and sales volume

forecasting can effectively control the production

plan of enterprises in a certain sense(Carbonneau et

al., 2008). Controlling inventory costs also plays a

crucial role in communicating with suppliers,

manufacturers, distributors, and other elements of the

supply chain (Ramos & Oliveira, 2023), so it is

necessary for the retail industry to find ways to

accurately predict sales volumes (Aburto, 2007). This

experiment will use Walmart as an example to

explore which prediction method is more effective. In

this paper, Wal-Mart is selected as a case for

prediction, and there are some profound

considerations. First of all, as one of the world's

largest retailers, Walmart has rich experience in

inventory management and also has rich experience

https://orcid.org/0009-0008-4522-5066

in upstream and downstream management of the

supply chain, and as one of the world's largest retail

enterprises, Wal-Mart can results to the fluctuation of

objective factors, so as to better evaluate the impact

of changes in objective factors on sales volume.

When discussing the impact of sales forecasts on

the supply chain of enterprises, people have to think

about the impact of the bullwhip effect on the supply

chain. The term bullwhip effect is used to describe the

slow change in consumer demand that has a greater

impact on suppliers at the other end of the supply

chain, and this impact will gradually amplify as the

supply chain deepens, and this effect is mainly

manifested in the fluctuation of production plans and

orders, which leads to unknown fluctuations leading

to higher production costs and inventory costs (Wang

& Disney, 2016). With the progress of management,

people have also found a lot of ways to solve the

bullwhip effect, sales forecasting is also one of them,

if the enterprise can predict the trend of customer

demand based on historical sales data, then the

enterprise can greatly reduce the impact of inventory

accumulation or insufficient inventory on the

enterprise (Boone et al., 2019).

The primary objective of this research is to

explore and compare the effectiveness of Polynomial

Regression and Random Forest (RF) models in the

542

Zhao, J.

Sales Forecasting in Retail Supply Chain Management.

DOI: 10.5220/0013270200004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 542-546

ISBN: 978-989-758-726-9

context of Walmart's supply chain, with a particular

focus on mitigating the bullwhip effect. Specifically,

this study will analyze the performance of these

models in predicting sales and their potential impact

on supply chain efficiency.

By evaluating the accuracy and robustness of

these models, the research aims to provide insights

into which methods are best suited for handling the

complexities of sales forecasting in a large-scale retail

environment. The findings from this study will

contribute to the ongoing efforts to optimize supply

chain operations and reduce the inefficiencies caused

by inaccurate demand predictions.

The remainder of this paper is organized as

follows. Section 2 presents the data collection

process, including data description and preprocessing

steps, as well as an overview of the models used for

sales forecasting. Section 3 details the results and

discussion, where the performance of each model is

evaluated, and the implications for supply chain

management are explored. Section 4 discusses the

limitations of the study and offers suggestions for

future research. Finally, Section 5 concludes the

paper by summarizing the key findings and their

relevance to improving supply chain efficiency in the

retail industry.

2 DATASETS

The data utilized in this study comes from Kaggle,

which includes weekly sales figures across various

stores in different regions. The data in this article

describes the sales data of 45 Walmart stores from

May 2, 2010, to October 19, 2012. Table 1 shows the

description of the dataset. Table 2 shows the

descriptive statistics of the dataset.

In terms of data integrity, there are a total of 6435

entries in this dataset, and there is no missing data or

feature, when processing the data, this experiment

conducts a detailed check on the data integrity

through the code, and no data is missing, and at the

same time, there is no duplication of the checked data.

In this experiment, a simple descriptive statistic

was performed on the data to better observe the data.

Before making data predictions, the data is pre-

processed to allow the experiment to be better

modeled. Data preprocessing is mainly divided into

the following four parts: data processing, feature

engineering, feature encoding, and data

standardization processing. Here's a closer look at the

data preprocessing part:

Firstly, the date data is processed by converting

the Date part into a format that can be used for

analysis. During this process, year, month, day, and

other relevant characteristics are extracted to

facilitate a better understanding of which factors have

the most significant impact on sales volume in

subsequent analyses. Next, feature engineering is

carried out by determining the season based on the

date of sale. The season is then used as an important

feature to analyze sales volume, alongside other

characteristics such as holidays, to study whether

these factors have a significant impact on sales. To

further improve the analysis, feature coding is

applied. This involves binary encoding of the store

identifiers and seasons, converting these features into

data types that are more suitable for analytical

Table 1: Data description.

Variable

Description

store Refers to the name of the sales store, identified b

numbers from 1 to 45.

Holiday

Indicates whether the date falls within a holiday period, as holidays can promote consumer spending and

are an important factor that may affect sales.

Tempe

ature

Records the average temperature of the week in the area where the store is located.

Fuel_Price

Specifically, it refers to the average price of oil in the area where the store is located during the week.

CPI

The relative number reflects the trend and degree of price changes of consumer goods and services

purchased by urban and rural residents during a period. It is the result of a comprehensive calculation of

the urban consumer price index and the rural consumer price index. This dataset refers to the average

CPI index in the United States during the week.

Unem

ment The unem

ment rate in the area where the store is located durin

the time

eriod.

Table 2: Descriptive statistics.

Feature Mean Standard Deviation Minimu

Maximu

Weekly_Sales 1,046,965.00 564,366.60 209,986.20 3,818,686.00

Temperature 60.66 18.44 -2.06 100.14

Fuel_Price 3.36 0.46 2.47 4.47

CPI 171.58 39.36 126.06 227.23

Unem

ment 7.99 1.88 3.88 14.31

Sales Forecasting in Retail Supply Chain Management

543

processing. Finally, data standardization is

performed, normalizing the individual data features

so that they all share the same dimensions, which is

crucial for the effectiveness of the subsequent training

and analysis phases.

3 MODEL

3.1 Model Selection

In this experiment, two models were selected,

Polynomial Regression (Heiberger et al., 2009) and

RF (Biau & Scornet, 2016), which have their own

advantages and disadvantages in processing data and

both models can build point prediction models at the

time of prediction (Hastie et al., 2009). Therefore, the

experiment will input different feature vectors at a

certain point in time to predict the sales volume.

Finally, the experiment will use the results of the two

models to compare the results of the two models in

predicting sales volume and observe which model can

better predict sales volume.

3.2 Polynomial Regression

This experimental model is affected by many factors,

as shown in the previous part of the data

characteristics, there are many other objective factors

that affect the sales volume, which may lead to the

model is not linear, so from a certain point of view,

the introduction of higher terms can better predict the

model, at the beginning of the experiment, the linear

model was used to predict, but the results are not ideal

as mentioned above, so the introduction of

polynomials is of great necessary. At the same time,

the model structure of Polynomial Regression is

relatively simple and easy to explain (Darlington &

Hayes, 2016).

In the process of Polynomial Regression model

construction, the experiment is not only a simple

construction of the model but also uses the network

search to optimize the hyperparameters of the

Polynomial Regression model to adjust the order of

the polynomial to find the optimal model.

3.3 Random Forest

Random Forests (RF) can also have a better

prediction effect for sales with multiple

characteristics, and they can capture these complex

relationships by randomly sampling features (Rigatti,

2017). The strong nonlinear modeling ability and

strong adaptability are also the reasons for choosing

this model in this experiment. Therefore, in this

experiment, RF is used to construct multiple decision

trees, and their prediction results are combined to deal

with high-level data and complex linear relationships.

4 EXPERIMENTAL PROCESS

4.1 Experimental Evaluation

Indicators

To compare the results of the two experimental

models and determine which model performs better,

research evaluated the experimental results using two

indicators: Root Mean Square Error (RMSE) and R-

squared ( R



). The specific formulas for these

indicators are provided in Equation (1) and Equation

(2).

RMSE =



𝑛





𝑦



−𝑦

















=1−

∑

𝑦



−𝑦











∑

𝑦



−𝑦













The 𝑦



means the actual value (true value), 𝑦



means the predicted value. 𝑦

means the mean of all

actual values,.In the formula, the actual sales are the

predicted sales, and n is the number of observations.

When the RMSE value is smaller, the better the

experimental results, the worse the performance of

the opposite model. These metrics were calculated for

both the training and testing datasets to evaluate the

models' performance and their ability to generalize to

unseen data.

When the value is closer to 1, the better the model

result, and the better the experimental result.

In addition, this paper uses cross-validation to

evaluate model performance. Cross-validation scores

are an important metric for evaluating the

generalization ability of machine learning models.

This indicator divides the dataset into k subsets, the

model is trained on a subset, and verified on the

remaining subset, repeated k times, so as to obtain k

performance indicators, the performance indicators

used in this paper are indicators, and after k indicators

are obtained, the overall performance of the model

and the stability of data division through the mean and

standard deviation of these k indicators, so as to

evaluate the generalization ability of the model in

predicting values.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

544

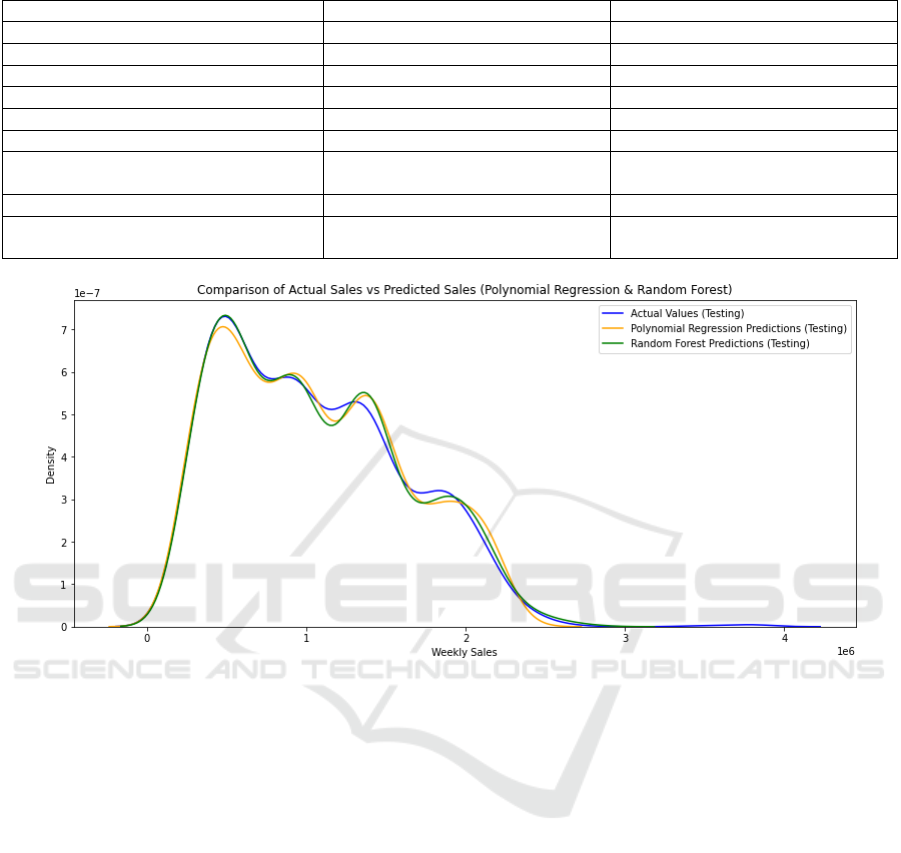
Table 3: Experiment results of polynomial regression and random forest.

Metrics Pol

nomial Re

ression Random Forest

Trainin

RMSE 75,434.78 52,066.51

Trainin

RMSE Error Scale 2.12% 1.65%

Training R-square

98.27% 99.15%

Testing RMSE 106,048.59 145,701.86

Testing RMSE Error Scale 3.21% 5.74%

Testin

R-s

uare

96.47% 93.41%

Cross-Validation Scores

[0.9567, 0.9585, 0.9623, 0.9634,

0.9581]

[0.9277, 0.9408, 0.9328, 0.9201,

0.9432]

Mean of Cross-Validation Scores 95.98% 93.29%

Standard Deviation of Cross-Validation

Scores

0.0026 0.0085

Figure 1: The models' prediction curves (Photo/Picture credit: Original).

4.2 Experimental Results

In the experiment, researchers used different degrees

of polynomials to fit the model to find a model that

took into account both accuracy and simplicity, in

order to find a better model, the experiment used the

hyperparameter tuning method to better fit the model,

The experimental results are shown in Table 3 and

Figure 1.

The X-axis represents the weekly sales values

(both actual and predicted). The Y-axis represents the

density or frequency of these sales values, indicating

how often different sales values occur within the

dataset.

For the training set, the RF model performed

better, with a smaller RMSE value and a value of R



closer to 1, while for the test set, the Polynomial

Regression model performed better, and in the cross-

validation score, the value of Polynomial Regression

is also significantly closer to 1 than that of the RF. In

some respects, the RF model is slightly overfitting

compared with the polynomial model, and the

generalization ability is poor in the face of more

complex and unknown sales models.

4.3 Feature Importance Analysis

Before using RF to predict sales, this paper used an

RF model to calculate feature importance. When

calculating importance, this paper arrives at an

importance score by evaluating the contribution of

each feature to the model's accuracy in the splitting of

the tree. The results of the feature importance analysis

are shown in Figure 2. In this analysis, this paper has

removed the influence of stores in the analysis of the

importance of characteristics because the difference

in stores due to regional and demographic factors can

greatly affect sales. In addition to the difference in

shops, CPI is the biggest factor affecting sales, the

unemployment rate is also an important factor

affecting sales, temperature, fuel prices and holidays

have a certain impact on sales, but compared to CPI

the unemployment rate has a small impact.

Sales Forecasting in Retail Supply Chain Management

545

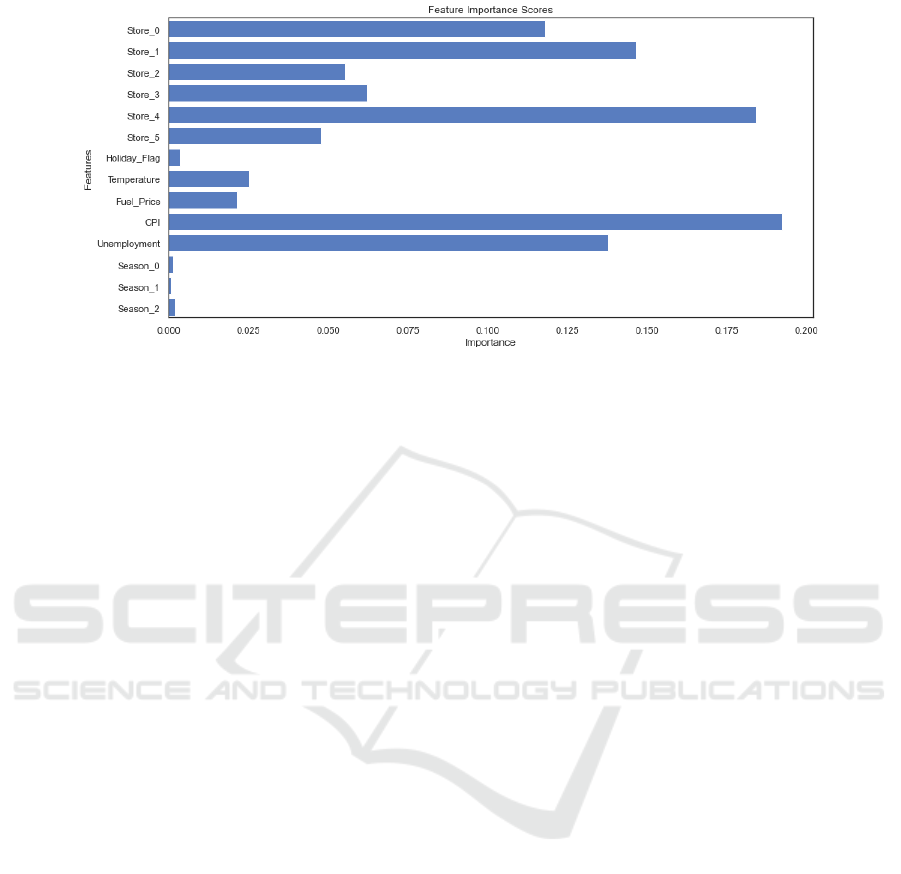
Figure 2: Feature Importance Scores (Photo/Picture credit: Original).

5 CONCLUSIONS

This study aimed to predict Walmart's sales volume

and assess which model better supports inventory

control, supply chain management, and mitigating the

bullwhip effect. Polynomial Regression and RF

regression were evaluated for prediction accuracy and

generalization ability. The results indicate that while

both models perform well, there are notable

differences. RF demonstrated superior performance

on the training set with lower RMSE and values

closer to 1. However, on the test set, Polynomial

Regression outperformed RF, with smaller RMSE

values and values nearer to 1. This suggests that

Polynomial Regression offers stronger generalization

capabilities. Cross-validation further confirmed that

Polynomial Regression maintains a higher average

value, indicating better prediction performance across

various scenarios. For retail supply chain

management, selecting a model with strong

generalization is crucial. Although RF shows better

fitting on training data, Polynomial Regression's

superior generalization makes it more suitable for

predicting sales in dynamic environments.

Nonetheless, this does not discount the potential of

RF or other models. Exploring additional data science

methods can address overfitting and enhance

generalization. Future research should integrate

supply chain management tools and strategies, and

evaluate a broader range of models - including LSTM

and other machine learning and deep learning

techniques - to improve prediction accuracy and

supply chain effectiveness.

REFERENCES

Biau, G., & Scornet, E., 2016. A random forest-guided tour.

Test, 25, 197-227.

Boone, T., Ganeshan, R., Jain, A., Sanders, N. R., 2019.

Forecasting sales in the supply chain: Consumer

analytics in the big data era. International journal of

forecasting, 35(1), 170-180.

Carbonneau, R., Laframboise, K., & Vahidov, R. (2008).

Application of machine learning techniques for supply

chain demand forecasting. European journal of

operational research, 184(3), 1140-1154.

Darlington, R. B., Hayes, A. F., 2016. Regression analysis

and linear models: Concepts, applications, and

implementation. Guilford Publications.

Koumanakos, D. P., 2008. The effect of inventory

management on firm performance. International

journal of productivity and performance

management, 57(5), 355-369.

Hastie, T., Tibshirani, R., Friedman, J., Hastie, T.,

Tibshirani, R., Friedman, J., 2009. Random forests. The

elements of statistical learning: Data mining, inference,

and prediction, 587-604.

Heiberger, R. M., Neuwirth, E., Heiberger, R. M.,

Neuwirth, E., 2009. Polynomial regression. R Through

Excel: A Spreadsheet Interface for Statistics, Data

Analysis, and Graphics, 269-284.

Ramos, P., Oliveira, J. M., 2023. Robust Sales forecasting

Using Deep Learning with Static and Dynamic

Covariates. Applied System Innovation, 6(5), 85.

Rigatti, S. J., 2017. Random forest. Journal of Insurance

Medicine, 47(1), 31-39.

Wang, X., Disney, S. M., 2016. The bullwhip effect:

Progress, trends and directions. European Journal of

Operational Research, 250(3), 691-701.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

546