Novel Portfolio Designs Based on Markowitz Portfolio Theory and

Various Assets

Robert Runze Hao

Stern School of Business, New York University, New York, U.S.A.

Keywords: Portfolio Optimization, Markowitz Theory, Mean-Variance Optimization, CAPM, Financial Economics.

Abstract: Portfolio is crucial for hedge the risks in contemporary assets management. This paper explores the

application of MPT in constructing and analysing portfolios using the top 10 U.S. companies from the Fortune

500. The study delves into the historical development and contemporary relevance of portfolio optimization,

building on foundational theories such as the CAPM (Capital Asset Pricing Model). Utilizing data sourced

from Yahoo Finance, the study applies advanced optimization techniques, including Global Minimum

Variance and Mean-Semivariance Optimization, to build the Efficient Frontier and evaluate portfolio

performance. The results indicate that the choice of optimization method significantly impacts portfolio

outcomes, with the Global Minimum Variance approach offering more stable returns, while the Mean-

Semivariance approach provides higher potential returns at the cost of increased volatility. The study's

findings underscore the significance of diversification and tailored risk management in modern investment

strategies. Nonetheless, the study recognizes constraints, including dependence on historical data and model

assumptions, suggesting avenues for future research in incorporating alternative risk measures and exploring

different economic environments. These results contribute to the field by providing both theoretical insights

and practical guidance for optimizing portfolios in today's dynamic financial markets.

1 INTRODUCTION

For the contributions to the subject of financial

economics, or finance, Harry Markowitz was

awarded the Nobel Prize. His investment framework

of Portfolio Selection, known as the MPT, made huge

impact and lays a solid foundation for extended study

on the portfolio selection (Mangram, 2013). For

example, the development of Sharpe ratio and the

CAPM in 1964, and the establishment of Fama

French Model in 1992. Contemporarily, scholars in

the field of finance continue to build on the topic of

portfolio selection. However, the theories and method

varies, portfolio selection evolves two central

measure: risk and return. MPT and all other following

theories are essentially looking for a more

sophisticated way to maximize its expected return and

minimize its risk of investment simultaneously.

(Markowitz, 1952; Markowitz, 1976)

The central theme of Economics is to find the

optimal way to allocate with limited resources given.

This idea applies to Financial Economics as well.

Portfolio Optimization, in its core, is to find an

optimal solution to allocate the limited financial

resources (usually calculated in dollar value) to

different financial assets or derivatives (stocks, bonds,

etc.) so that the portfolio produce the most yield at a

specific risk. Today, the step of finding the optimal

weights can be easily done using Python, Excel

Solver, or any other similar product. So, the key

question for modern investor is to select the assets and

derivatives that he would like to invest in.

The CAPM is a highly significant and thoroughly

examined framework in contemporary finance.

Created in 1964 by William Sharpe, the CAPM offers

a methodology for evaluating an asset's E[R] in light

of its market risk. It is based on the principles

established by MPT, which introduced diversification

to mitigate risk in an asset portfolio. The CAPM

correlates the anticipated return of an asset with its

systematic risk, denoted by the beta coefficient (β),

which quantifies the return of an asset in relation to

market returns. The fundamental principle of CAPM

asserts that investors must receive compensation in

two forms: the time value of money and risk. The Rf,

which is the return on a risk-free investment typically

linked to government bonds, is a symbol for the time

value of money. The risk element is represented by

504

Hao, R. R.

Novel Portfolio Designs Based on Markowitz Portfolio Theory and Various Assets.

DOI: 10.5220/0013269500004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 504-509

ISBN: 978-989-758-726-9

the risk premium, defined as the disparity between the

anticipated market return (E[Rm]) and the risk-free

rate. The CAPM formula is articulated as:

𝐸[𝑅𝑖]=𝑅𝑓 + 𝛽𝑠(𝐸[𝑅𝑚] −𝑅𝑓) (1)

Here, βs indicates the investment's beta, E[Ri] is the

expected return on investment, Rf is the risk-free rate,

and (E[Rm] - Rf) is the market risk premium. This

formula shows that an asset's expected return is

closely correlated with its systematic risk, which is

measured by beta. The CAPM holds considerable

significance for asset valuation and portfolio

administration. Initially, it establishes a standard for

evaluating investment performance. Investors can

ascertain if an asset is overvalued or undervalued by

contrasting its actual return with the expected return

forecasted by CAPM. CAPM aids in determining the

capital cost, which is essential regarding corporate

finance choices, including capital allocation and

project assessment (Fama & French, 2004).

Even with its extensive usage, CAPM has been

the focus of many debates and criticism. One of the

primary criticisms is its reliance on several

simplifying assumptions, like the presence of an asset

devoid of risk, the notion that the expectations of all

investors are the same, and that markets are perfectly

efficient. These assumptions, while useful for

creating a tractable model, are often unrealistic in

real-world settings (Black, Jensen, & Scholes, 1972).

Research studies analysing the CAPM empirically

have produced conflicting results. Research

conducted by Fama and French demonstrates that

variables beyond beta, including business size and the

book-to-market ratio, significantly influence stock

returns, hence contesting the CAPM's assertion that

beta is the exclusive predictor of projected returns

(Fama & French, 1992). The model's validity has

been scrutinized at times of market upheaval,

including the global financial crisis of 2007-2008 and

the COVID-19 pandemic. In these circumstances, the

presumption of a consistent, foreseeable correlation

between risk and return may falter, resulting in

substantial divergences from the anticipated results

forecasted by CAPM (Maji, 2012).

Despite these criticisms, CAPM remains a key

building block of modern finance theories. Its

simplicity, intuitive appeal, and foundational role in

understanding the risk-return tradeoff have ensured

its continued relevance in both academic research and

practical applications. However, it is widely

recognized that CAPM is not a universally applicable

solution, and its limitations must be considered when

applying it to real-world scenarios. As finance

continues to evolve, CAPM serves as a foundational

model upon which more complex and nuanced

models have been built, reflecting the intricate

realities of financial markets.

The motivation for this paper stems from the

critical importance of portfolio optimization in

modern finance, particularly in the context of large,

influential corporations. MPT provides a robust

structure for developing an ideal portfolio through

weighing return and risk. Given the prominence and

substantial market impact of the top 10 U.S.

companies in the Fortune 500, analysing their

performance through the lens of Markowitz's theory

offers valuable insights into risk management and

investment strategies. These companies, which

include industry leaders across sectors such as

technology, healthcare, and finance, are often seen as

bellwethers of the broader economy. Investors, both

institutional and individual, frequently look to these

companies when constructing portfolios, making it

essential to understand how to increase profits while

lowering risk in this context. By applying

Markowitz's theory, which emphasizes the

importance of diversification and the efficient frontier,

this paper seeks to investigate the optimal allocation

of investment among these top-performing firms.

Furthermore, the post-pandemic economic

landscape has introduced new variables and

uncertainties that challenge traditional investment

strategies. The top 10 Fortune 500 companies have

shown varying degrees of resilience and growth

during this period, offering a unique opportunity to

test the robustness of Markowitz's model in a

contemporary setting. By studying these companies,

this essay aims to further the current conversation

regarding the relevance and application of MPT in

today's dynamic financial environment, providing

both theoretical insights and practical guidance for

investors aiming to optimize their portfolios. This

research not only reinforces the importance of

diversification but also highlights the evolving nature

of risk in modern financial markets.

2 DATA AND METHOD

This study employs a rigorous methodological

framework rooted in Markowitz's Mean-Variance

Optimization, a central concept in MPT. The

objective is to optimize the portfolio of the top 10 U.S.

companies by minimizing risk while maximizing

expected returns. The methodology is outlined as

follows. The data comprises daily prices for the top

10 U.S. companies, sourced using the ‘yfinance’

library from Yahoo Finance, which is widely

regarded for its accuracy in providing historical

Novel Portfolio Designs Based on Markowitz Portfolio Theory and Various Assets

505

financial data. These companies, spanning sectors

such as technology, healthcare, and finance, represent

a substantial portion of the U.S. market. Adjusted

closing prices were collected to calculate daily returns,

which are critical for the portfolio optimization

process (Brown & Warner, 1985; Fama, 1970).

Expected returns were estimated using the CAPM,

which adjusts for systematic risk and provides a more

reliable estimate compared to simple historical

averages (Sharpe, 1964). The covariance matrix, a

crucial component in portfolio optimization, was

estimated using the Ledoit-Wolf shrinkage method.

This method is preferred over the traditional sample

covariance matrix due to its ability to reduce

estimation error and enhance robustness (Ledoit &

Wolf, 2004; DeMiguel, Garlappi, & Uppal, 2009).

For Global Minimum Variance (GMV) Portfolio,

it was constructed with the aim of minimizing the

total portfolio variance. This approach allows for both

long and short positions, ensuring that the portfolio

achieves the lowest possible risk (Markowitz, 1952;

Clarke et al, 2006). The study also employed mean-

semivariance optimization, which focuses on

minimizing downside risk rather than total volatility,

aligning more closely with the risk preferences of

conservative investors (Estrada, 2007). This method

identifies portfolios that minimize potential losses,

offering a more targeted approach to risk

management. The final stage of the methodology

involved constructing and analyzing The efficient

frontier denotes the collection of optimal portfolios

that provide the maximum expected return for a

specified level of risk. This was achieved under

various constraints, including sectoral and regulatory

constraints, to ensure the theoretical soundness and

practical applicability of the findings (Michaud, 1989;

Jorion, 1992).

This methodologically robust approach facilitates

a comprehensive evaluation of portfolio performance,

providing valuable insights into optimal allocation

strategies among the top 10 U.S. companies. The use

of advanced techniques, such as shrinkage estimation

and alternative risk measures, enhances the

robustness of the findings and contributes

significantly to the existing literature on portfolio

optimization.

3 RESULTS AND DISCUSSION

3.1 Effective Frontier

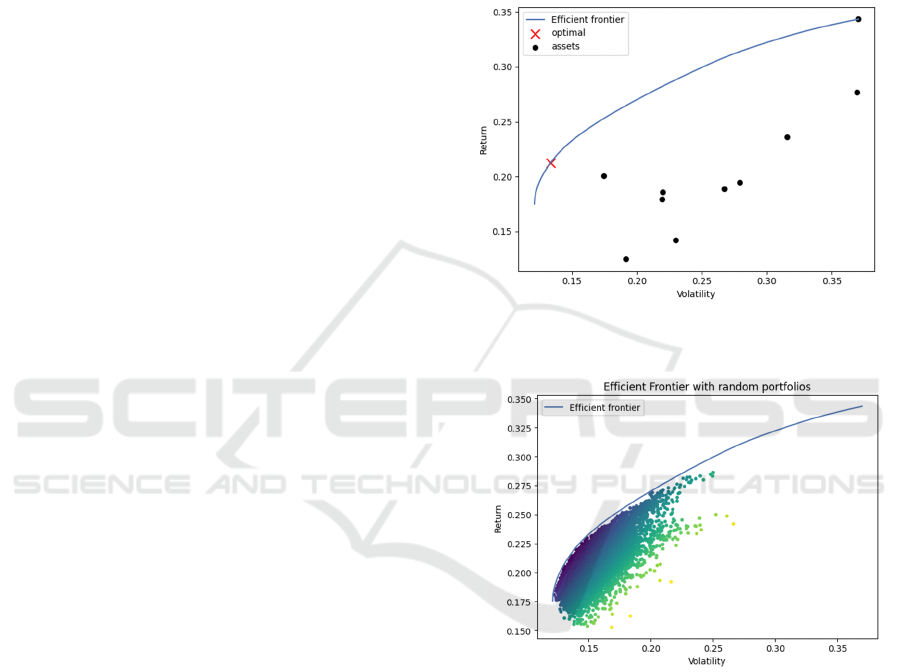
The Efficient Frontier is a core principle in MPT,

denoting the collection of optimum portfolios that

provide the maximum expected return for a specified

degree of risk. In this study, the Efficient Frontier

was constructed by applying different optimization

techniques to the top 10 U.S. companies in the

Fortune 500. The portfolios were optimized to

minimize risk while maximizing return, using data on

daily returns calculated from historical prices. The

results for optimal and random portfolios are shown

in Figure 1 and Figure 2, respectievly.

Figure 1: Efficient Frontier with Assets and Optimal

Portfolio (Photo/Picture credit: Original).

Figure 2: Efficient Frontier with Random Portfolios

(Photo/Picture credit: Original).

3.2 Model Performance

To assess the efficacy of different optimization

functions, the study employed several portfolio

optimization techniques, including Global Minimum

Variance and Mean-Semivariance Optimization.

These methods were applied to the dataset to

construct portfolios under varying risk constraints,

and their performance was subsequently analyzed.

Here is a statistical summary of the portfolio

performance under different optimization techniques.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

506

The expected annual return of 20.0% indicates a

strong performance projection, while the annual

volatility of 9.6% reflects the portfolio's risk level.

The Sharpe ratio of 1.87 suggests that the portfolio

offers a high return per unit of risk, making it an

attractive option for risk-averse investors.

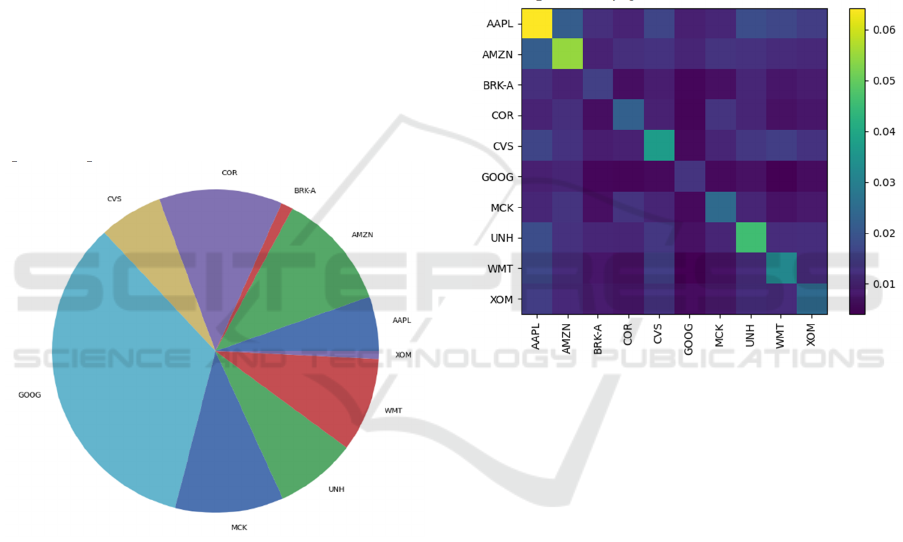
Additionally, the portfolio weights resulting from the

optimization process are visually represented in

Figure 3. Figure 3 provides a bar chart illustrating the

asset allocation across the top 10 companies. The

horizontal bars represent the proportional investment

in each company, highlighting the diversification

strategy employed in the optimization process.

Notably, companies like Google (GOOG) and

Berkshire Hathaway (BRK-A) have the largest

weights in the portfolio, reflecting their influence in

maximizing returns while maintaining an acceptable

risk level. On the other hand, companies like Amazon

(AMZN) and Apple (AAPL) have relatively smaller

weights, which may be due to their higher volatility

or lower expected returns in the context of the

optimized portfolio.

Figure 3: Portfolio Weights (Photo/Picture credit: Original).

The covariance matrix, shown in Figure 4, further

elucidates the relationships between the assets in the

portfolio. Figure 4 demonstrates the correlation

between the daily returns of each pair of companies

in the portfolio. The color intensity in the heatmap

indicates the strength of the covariance, with brighter

colors representing higher covariance values. For

example, companies such as Apple (AAPL) and

Amazon (AMZN) exhibit a relatively higher

covariance, suggesting that their returns generally

exhibit a tendency to move in the same direction.

Conversely, some pairs like CVS and XOM show

lower covariance, indicating less synchronized

movements in their returns.

Understanding these covariances is crucial for

effective portfolio optimization, as it allows for better

diversification by combining assets that do not move

together. This reduces the overall portfolio risk while

still achieving a desirable return. These results

indicate that the choice of optimization method

significantly affects portfolio performance. The high

Sharpe ratio suggests that the portfolio optimization

process effectively balances risk and return,

particularly for the Global Minimum Variance

approach, which is preferable for risk-averse

investors seeking steady returns with minimal risk. In

contrast, the Mean-Semivariance optimization is

more suited for investors willing to tolerate higher

risk for potentially greater returns.

Figure 4: Covariance Matrix(Photo/Picture credit: Original).

3.3 Explanation and Implications

The findings from the portfolio optimization

highlight the critical role of risk management in

constructing an efficient portfolio. The Efficient

Frontier clearly demonstrates that higher returns are

achievable only with higher levels of risk,

emphasizing the importance of diversification in

mitigating volatility. Investors should carefully

consider their risk tolerance when selecting portfolios,

as those positioned on the upper end of the Efficient

Frontier are more exposed to market fluctuations.

The high Sharpe ratio of 1.87 indicates that the

optimized portfolio is expected to generate returns

significantly above the risk-free rate, adjusted for

volatility. This suggests that the portfolio is well

constructed, offering substantial returns relative to its

risk level. Investors should note that such a portfolio

is particularly attractive in stable market conditions

but should be monitored closely at times of volatility

in the market.

Novel Portfolio Designs Based on Markowitz Portfolio Theory and Various Assets

507

From a practical perspective, the study provides

several investment insights. Portfolios that include a

mix of low-volatility and high-growth companies

attain a more advantageous ratio of return to risk. The

diversification is evident in the portfolio weights

illustrated in Figure 3, where investments are spread

across different sectors. The portfolio's relatively low

volatility of 9.6% suggests effective risk management,

which can lead to more consistent performance over

time, particularly in volatile markets. Investors

seeking higher returns may consider strategies that

optimize for semivariance, but they must be prepared

for the accompanying increase in portfolio volatility.

These implications reinforce the notion that portfolio

optimization is not a strategy that works for every

scenario; instead, it must be customized to the

particular risk-return profile of the investor.

3.4 Limitations and Prospects

While this study provides valuable insights into

portfolio optimization using the top 10 U.S.

companies, there are several limitations that warrant

discussion. The analysis depend upon historical price

data, which may not fully capture future market

dynamics or account for unprecedented events such

as economic crises or pandemics. In addition, the

optimization techniques used in this study are based

on certain assumptions, such as normally distributed

returns and constant covariances, which may not hold

true in all market conditions. Besides, the study

focuses on the top 10 U.S. companies, which, while

representative of the broader market, may not reflect

the performance of smaller or less prominent firms.

Future research could expand on this work by

exploring different asset classes, incorporating

alternative risk measures such as Value at Risk (VaR),

and applying these methods in different economic

environments. Additionally, examining the impact of

external factors like interest rate changes or

geopolitical events on the Efficient Frontier could

provide further insights into portfolio optimization

strategies.

4 CONCLUSIONS

To sum up, this study applied Markowitz's Mean-

Variance Optimization to construct and analyse

efficient portfolios using the top 10 U.S. companies

in the Fortune 500. The results demonstrate that

portfolio performance is highly dependent on the

choice of optimization method, with the Global

Minimum Variance approach offering more stable

returns and the Mean-Semivariance approach

providing higher potential returns at the cost of

increased volatility. The study’s limitations include

reliance on historical data and the assumptions

underlying the optimization models, which may not

fully capture real-world market complexities. Future

research should consider incorporating more diverse

data sources and risk measures to enhance the

robustness of portfolio optimization models. This

research contributes to the field by supplying a

practical framework for investors to effectively

balance return and risk, emphasizing the importance

of diversification and tailored risk management

strategies in portfolio construction.

REFERENCES

Alexander, G. J., 2013. From Markowitz to modern risk

management. Asset Management and International

Capital Markets, 5-15.

Black, F., Jensen, M. C., Scholes, M., 1972. The Capital

Asset Pricing Model: Some empirical tests. Studies in

the Theory of Capital Markets, 79-121.

Chakrabarty, N., Biswas, S., 2019. Strategic Markowitz

portfolio optimization (SMPO): a portfolio return

booster. 2019 9th Annual Information Technology,

Electromechanical Engineering and Microelectronics

Conference (IEMECON), 196-200.

Fama, E. F., French, K. R., 1992. The cross-section of

expected stock returns. The Journal of Finance, 47(2),

427-465.

Fama, E. F., French, K. R., 2004. The capital asset pricing

model: Theory and evidence. Journal of economic

perspectives, 18(3), 25-46.

Guerard Jr, J. B., 2009. Handbook of portfolio construction:

contemporary applications of Markowitz techniques.

Springer Science & Business Media.

Hali, N. A., Yuliati, A., 2020. Markowitz model investment

portfolio optimization: a review theory. International

Journal of Research in Community Services, 1(3), 14-18.

Hanif, A., Hanun, N. R., Febriansah, R. E., 2021.

Optimization of stock portfolio using the markowitz

model in the era of the COVID-19 pandemic.

International Journal of Applied Business, 5(1), 37-50.

Kamil, A. A., Fei, C. Y., Kok, L. K., 2006. Portfolio analysis

based on Markowitz model. Journal of Statistics and

Management Systems, 9(3), 519–536.

Litterman, B., 2003. Modern investment management: an

equilibrium approach. John Wiley & Sons.

Maji, S. G., 2012. The predictive power of CAPM: An

empirical analysis. Asian Journal of Finance &

Accounting, 4(1), 72-82.

Mangram, M. E., 2013. A Simplified Perspective of the

Markowitz Portfolio Theory. Global Journal of

Business Research, 7(1), 59-70.

Markowitz, H., 1952. Portfolio selection. The Journal of

Finance, 7(1), 77-91.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

508

Markowitz, H., 1976. Markowitz revisited. Financial

Analysts Journal 32.5 (1976): 47-52.

Sharpe, W. F., 1964. Capital asset prices: A theory of

market equilibrium under conditions of risk. The

Journal of Finance, 19(3), 425-442.

Širůček, M., Křen, L., 2017. Application of Markowitz

portfolio theory by building optimal portfolio on the US

stock market. Tools and Techniques for Economic

Decision Analysis, 24-42.

Novel Portfolio Designs Based on Markowitz Portfolio Theory and Various Assets

509