Construction of Novel Portfolio Based on Modern Portfolio Theory

Yundi Zhang

Department of Accounting & Finance, University of Birmingham, Birmingham, U.K.

Keywords: Modern Portfolio Theory, Efficient Frontier, Sharpe Ratio, Monte Carlo Simulations, Portfolio Optimization.

Abstract: Modern Portfolio Theory (MPT) suggesting diversifying portfolios to reach an optimal trade-off between

returns and risks is the footstone of practical financial investments. Nowadays, portfolio construction has

continuously embraced novel types of assets to enhance returns and manage risks rather than solely containing

traditional stocks and bonds. This study constructs a novel portfolio under the MPT framework and discusses

weight allocation to make the portfolio the most efficient. One hundred thousand Monte Carlo simulations

are carried out to discover the Efficient Frontier, and the Solver technique in Excel is used to put constraints

on objective functions to draw the Capital Market Line (CML). The allocation of portfolios with the highest

Sharpe Ratio, the highest return and the minimum volatility, has been explained and discussed. For results,

investors who want to optimize their portfolios and have a certain level of risk tolerance should focus more

on cryptocurrency and specific futures. This study may benefit investors interested in novel assets in markets

by having a clearer understanding of their weight allocation according to their preferences.

1 INTRODUCTION

Nowadays, with the improvement of economics,

increasing people make their own investments to gain

returns. In retrospect, the idea of Modern Portfolio

Theory was introduced by Markowitz, which is the

fundamental footstone of practical financial

investments. Modern Portfolio Theory suggests that a

diversified portfolio can spread out risk and attain an

optimal return through asset allocation (Markowitz,

1952). This idea lets investors no longer focus on sole

asset investment as before but start to increase the

variety of assets in the portfolio to reduce risk. Also,

the correlation between assets is a crucial factor.

Investors try to avoid highly correlated securities as

this will increase the volatility of investments. In the

same year, Roy introduced the Safety-First Portfolio

Theory, which minimizes the possibility of returns

falling below a specific threshold (Roy, 1952). The

Minimum Variance Model was then introduced in

1959 by Markowitz as a result of this theory,

minimizing the volatility in the constructed portfolio

(Markowitz, 1959). Later, Sharpe introduced the

famous Capital Asset Pricing Model, which outlined

the method for appropriately determining the prices

of securities based on their risks (Sharpe, 1964). The

Black-Litterman model by Black and Litterman can

deal with real-life investment situations (Black &

Litterman, 1990). Meanwhile, Jorion introduced the

Value at Risk model to calculate the maximum

potential loss of investment (Jorion, 1997).

Contemporarily, the portfolio construction theory has

been continuously enhanced and applied in many

aspects. For example, more customized investment

decisions can be made utilizing big data and artificial

intelligence, which facilitates more accurate

evaluations of market trends (Kearns & Nevmyvaka,

2013). Furthermore, the inclusion of environmental,

social, and governance (ESG) factors has become

essential in the process of building investment

portfolios, making investment choices contributed at

social levels to some certainty (Friede et al., 2015). In

recent years, with the improvement of portfolio

theory, a variety of classes of novel assets, such as

cryptocurrencies, exchange-traded commodities

(ETCs), green bonds, and new index-tracking ETFs

etc., have come out in the market. Baur and Lucey

state that cryptocurrencies can be seen as a hedge that

is not influenced by market fluctuations (Baur &

Lucey, 2010). Therefore, they are not as vulnerable

when undergoing a financial crisis as equity

investments. This is the characteristic of

cryptocurrencies and also the reason why

cryptocurrencies tend to have high prices and

demand. Gorton and Rouwenhorst claimed that ETCs

allow portfolios to protect against inflation by

Zhang, Y.

Construction of Novel Portfolio Based on Modern Portfolio Theory.

DOI: 10.5220/0013269300004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 491-495

ISBN: 978-989-758-726-9

491

granting access to commodities through traditional

stock exchanges (Gorton & Rouwenhorst, 2006). The

reason is that commodities are independent of the

movement of equity under inflation. Therefore,

considering long-term influence, investors can

allocate weight to ETC to hedge inflation influence.

The characteristic of green bonds is that they align

investment portfolios with sustainability goals (Baker

& McClain, 2019). Investors who prioritize ethical

and environmental development prefer allocating

weight to it. It shows not only the returns but also the

contribution to the social environment. The achieved

research on these novel types of assets all shows their

unique characteristic influencing the final decision

investors make.

In order to further research this concern, this paper

will construct a portfolio consisting of five novel

assets and see how the portfolio is influenced by the

different weight allocations of these securities. The

following part will discuss the data and methodology

used, evaluate the model performance, explain the

empirical results, and propose limitations and

prospects for the future. The results presented may

shed light on certain investors interested in novel

portfolios in the financial markets.

2 DATA AND METHOD

In this paper, datasets were collected from Yahoo

Finance (2024). To be specific, the portfolio contains

five classes of novel securities, and each class

selected a representative company to construct. They

are respectively the ETC from SparkChange Physical

Carbon EUA (CO2U.L), stock equity from Tesla

(TSLA), ETF from iShares ESG Aware MSCI EAFE

(ESGD) tracking the performance of the MSCI EAFE

ESG Focus Index, cryptocurrency Bitcoin USD

(BTC-USD) and Crude Oil Futures (CL=F). In the

remaining part of this paper, they are referred to by

their tickers. Weekly historical data were chosen from

20 Oct. 2021 to 20 Aug. 2024 to reflect returns. It

should be noted that the tracking period is less than

three years because the subject CO2U.L is too novel,

so its public trading time can only be traced back to

18 Oct. 2021.

This study aims to construct an investment

portfolio with the maximum Sharpe Ratio as its

objective function optimization. The Sharpe ratio

measures the expected excess return divided by the

overall portfolio risk. This metric can accurately

quantify the efficiency of portfolio returns in relation

to the risks undertaken. Therefore, it needs to find the

most appropriate weight allocation by maximizing

the Sharpe Ratio value. Following are the steps

employed to figure out the proper weights for

portfolio optimization. First of all, weekly adjusted

closing prices are used to calculate the average

returns of five securities and then convert them into

annualized ones. Then, a covariance matrix of these

five securities needs to be shown. Afterwards, Monte

Carlo simulations are carried out to generate random

variables for each of their weight allocation. Monte

Carlo simulations use random variables to calculate

results over and over to conduct a quantitative risk

analysis (Glasserman, 2003). This forecasting model

is innovative and highly adaptable, allowing for

adjustments based on changing investment

objectives. One hundred thousand Monte Carlo

simulations were carried out in this paper to optimize

the Sharpe Ratio. Values of random weight variables

are all larger than zero and less than one. Besides,

constraints were put to avoid some extreme

situations. Specifically, the sum of the weights of five

securities is always equal to one. Next, the expected

portfolio return and portfolio risk can be calculated as

follows:

𝐸𝑅



= Σ





𝜔



𝐸



𝑟





(1)

𝜎













𝜔



𝜔



Covr





 (2)

where 𝜔



represents the security weights, E(r

) is the

expected returns (annualized) and Cov(r

, r

) is the

covariance of five securities. Then, the standard

deviation needs to be converted into the annualized

value. Finally, the Sharpe Ratio can be calculated as

follows:

𝑆ℎ𝑎𝑟𝑝𝑒 𝑅𝑎𝑡𝑖𝑜 =













(3)

where R

is the risk-free rate during this 3-year period.

Values of 10-year treasury bonds were used to

calculate R

3 RESULTS AND DISCUSSION

3.1 Efficient Frontier

The Efficient Frontier was derived by applying Monte

Carlo methods to simulate 10,000 portfolio

combinations. These combinations were then plotted

on a graph, with the expected returns on the y-axis

and the standard deviation on the x-axis. The graph

(Figure 1) below depicts the trade-off between

portfolio risk and expected return, showcasing

portfolios on the frontier that optimize returns for a

specific level of risk. Figure 1 is the scatter plot of

portfolio return and standard deviation consisting of

one hundred thousand Monte Carlo simulations. The

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

492

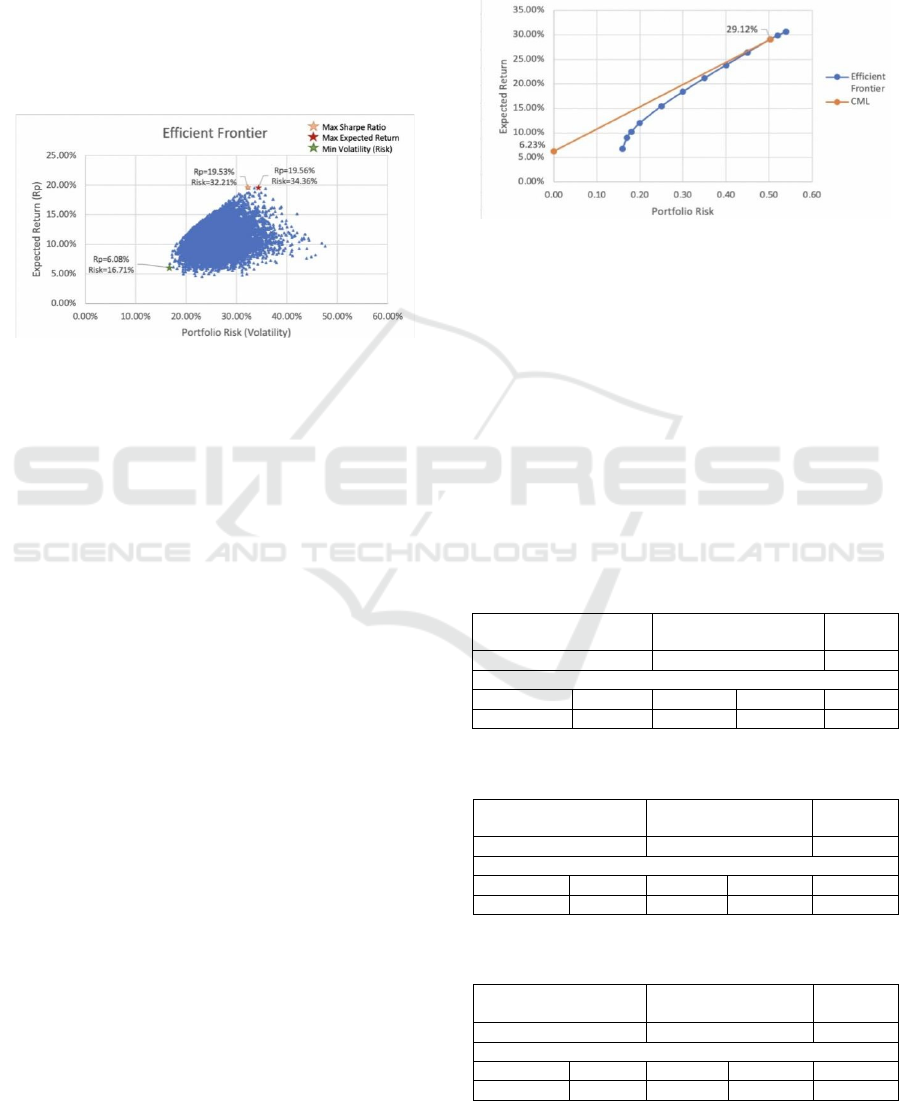
graph illustrates that most of the portfolio

combinations have a 20% to 40% risk and generate

5% to 20% expected returns. Applying portfolio

theory and using the Monte Carlo simulations make it

possible to figure out the portfolio’s efficient frontier.

Any portfolios that are just on the line can have the

optimal returns under that particular level of risk. In

contrast, any investment combinations inside the

efficient frontier can be reached whether with a

higher return under the same volatility or with lower

volatility under the same return.

Figure 1: Portfolio Efficient Frontier using Monte Carlo

simulations (Photo/Picture credit: Original).

Three portfolio combinations marked with stars in

Figure 1 are noticeable. The combination with the

highest expected return is 19.56% and a 34.36%

volatility. Compared to the highest expected return

(19.56%), the investment with the highest sharp ratio

(48.90%) is on the efficient frontier and its expected

return and volatility are 19.53% and 32.21%,

respectively. The nearly identical return value and

more minor volatility optimize this portfolio and

make it more efficient than the one with the highest

expected return under a certain risk level. Another

combination has the lowest volatility (16.71%) and a

6.08% return.

3.2 Model Perofopmances

The Monte Carlo simulations were utilized to depict

the efficient frontier, providing a macroscopic view

of portfolio investment performance across different

risk levels through a large number of randomly

generated portfolio combinations. Then, in Section

3.2, the Solver tool in Excel will be used to fine-tune

the investment. Specifically, 20% of the weight is

assumed to be equally allocated to each security.

Then the maximum Sharpe Ratio, maximum returns,

and minimum volatility will be seen as the objective

functions in discussing the portfolio, ensuring the

portfolio aligns with the Capital Market Line (CML).

This method provides a microscopic view of the

portfolio and enhances its practicality. It is worth

mentioning that a restriction will be put in place: the

weight of each asset is between -1 and 1, but the total

weight of the total five assets is always 100%. Unlike

Monte Carlo random variables where the value is 0 to

1, the weight can be a negative value here. Its specific

meaning will be explained in the next section.

Figure 2: CML and Efficient Frontier using the Solver

(Photo/Picture credit: Original).

As depicted in Figure 2, the blue line is the

efficient frontier showing portfolios with the highest

expected return possible for a given level of risk

under the Solver technique. The orange line is the

CML, which is tangent to the efficient frontier at the

highest Sharpe Ratio point. The point with the highest

Sharpe Ratio is just lying on the efficient frontier,

which is the portfolio optimization point, with a

29.12% expected return and a 50.32% volatility. The

following section is going to use Portfolio A to refer

to the one with the highest Sharpe Ratio.

Table 1: Portfolio Combination A with Maximum Sharpe

Ratio.

Expected Rerturn Sharpe Ratio

Portfolio

Ris

29.12% 50.36% 50.32%

Coefficients

CO2U.L TSLA ESGD BTC-USD CL=F

100% -5.74% -43.25% 49.82% -0.83%

Table 2: Portfolio Combination B with Maximum Expected

Return.

Expected Rerturn Sharpe Ratio

Portfolio

Ris

38.64% 33.37% 104.45%

Coefficients

CO2U.L TSLA ESGD BTC-USD CL=F

100% 100% -100% 100% -100%

Table 3: Portfolio Combination C with Minimum

Volatility.

Expected Rerturn Sharpe Ratio

Portfolio

Ris

6.23% 15.96% 15.38%

Coefficients

CO2U.L TSLA ESGD BTC-USD CL=F

5.74% -3.62% 77.91% 4.43% 15.54%

Construction of Novel Portfolio Based on Modern Portfolio Theory

493

As listed in Table 1, the Sharpe Ratio of Portfolio

A is 50.36%, showing its different weight allocation

on five assets in the portfolio. It shows a high

concentration of CO2U.l, which is 100% fully

invested. Also, the cryptocurrency is worth nearly

half (49.82%) weight. The other three securities are

considered to have a pessimistic expectation for the

future, so short selling can be taken as a measure to

provide a hedge for portfolio A. ESGD accounts for

the largest negative weight (-43.25%) among these.

Similar to Portfolio A, Portfolio B and Portfolio C

are also special combinations that represent the one

with the maximum expected return and the one with

the minimum standard deviation. As shown in Table

2, the highest expected return can be achieved is

38.63% and has a 33.37% Sharpe Ratio. If investors

mindlessly pursue high returns and do not take risks

into account, there will be an extreme situation. 100%

Fully investing and short selling these five securities

result in a significant volatility of up to 104.45%,

meaning the return range can be from a negative

65.82% to 143.08%. Compared to Portfolio B,

Portfolio C shows the smallest volatility. In this

combination, ESGD is heavily invested in up to

77.91%, ETC, cryptocurrency and futures are also

allocated with appropriate proportions respectively.

TSLA stock equity is again shorted (-3.62%). This

weight allocation generates a relatively low expected

return (6.23%) and a 15.38% Sharpe Ratio, which

seems not to be an efficient choice as given in Table

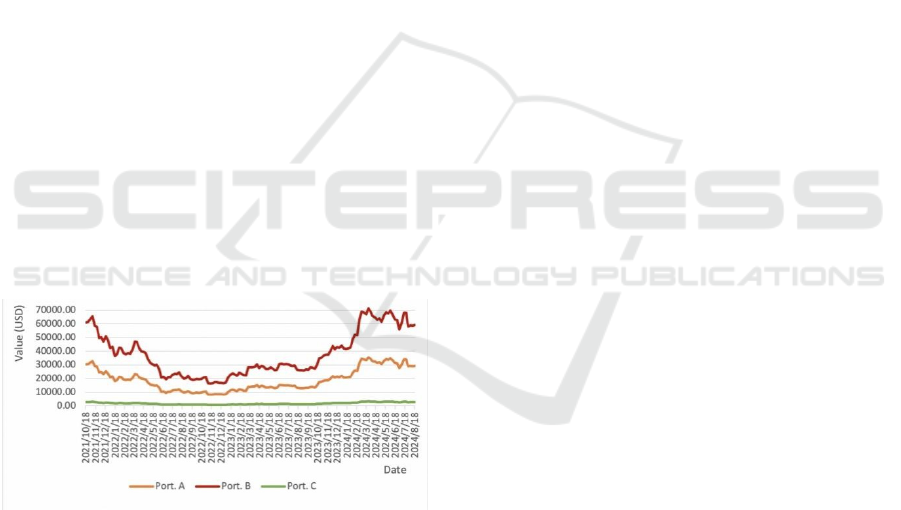
Figure 3: Net Asset Value (NAV) Curve of three Portfolios

(Photo/Picture credit: Original).

The Net Asset Value (NAV) curve of the three

portfolios is shown below. It depicts the portfolio’s

performance over the period from Oct. 2021 to Aug.

2024. The assumption is that the investing proportion

stays the same for three years. From Figure 3, all these

three portfolios exhibit a trend of falling sharply first

and then recovering and even rising until now,

showcasing their resilience. Comparatively, the three

portfolios show different volatility. Portfolio B is

more volatile, ranging from $16403 to $71411,

showing portfolio B is capable of earning higher

gains but facing higher downside risks. In contrast,

portfolio C generates the lowest value ($1000 to

$3000) and volatility, suitable for risk advisors who

prefer steady returns.

3.3 Explanation and Implications

Refocusing on Portfolio A, the reason that having a

maximized Sharpe Ratio may be due to it investing

heavily in securities such as cryptocurrency, which

are more profitable, and it also short other classes of

securities to provide a hedge to avoid significant

potential losses that high-growth assets bring.

Investors who want to optimize their portfolio can

take the weight allocation of the Sharpe Ratio point

as a reference.

From the above analysis, some insights and

investment implications can be given. The CML and

efficient frontier help investors reach a balance

between returns and risks. Investors can pay more

attention to the carbon EUA ETC and the bitcoins

when constructing portfolios, meanwhile focusing on

volatility. In addition to this, risk tolerance also

matters. Risk advisors such as seniors may prefer

lower risk and steady returns, so they may choose

Portfolio C over Portfolio A. In comparison, risk

seekers may be willing to accept the largest volatility

for higher returns, such as Portfolio B. Therefore,

when constructing portfolios, investors should not

only be concerned about the efficiency of diversified

securities but also consider personal preferences and

market conditions before making investment

decisions.

3.4 Limitations and Prospects

In this part, the limitations of the portfolio

optimization model and methods will be discussed, as

well as the future prospects will be mentioned for

further research. The most significant problem is that

the model uses historical data to forecast. However,

historical data cannot be representative of future

results as future results will be affected by the market

moment-by-moment. Using historical prices can

generate inaccurate returns, standard deviation, and

covariance matrix. Additionally, the subject of this

paper is a novel portfolio, thus some securities do not

have enough data, such as the crude oil futures, which

only have public trading prices that are less than three

years. The limited period cannot reflect the trend well

compared to a long-lasting period (more than ten

years). Also, not all types of risks can be included in

the model when calculating the Sharpe Ratio. Risks

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

494

include credit risk, urgent financial crisis and so forth.

It takes time to transmit market information to have a

reflection on prices in a semi-strong efficient market.

Future research can explore the model to have the

ability to capture some information and events

influencing market dynamics and consider some

economic factors. Moreover, new models such as

price prediction and risk evaluation that can forecast

future results more accurately should be enhanced.

4 CONCLUSIONS

In conclusion, this paper investigates a portfolio

based on five novel assets, including ETC, new-

energy stock, ETF, cryptocurrency, and futures. First,

previous literature is reviewed to illustrate the history

of portfolio development and current situations. For

investigation, all weekly price data are collected from

Yahoo Finance (2024). Then, one hundred thousand

returns and risks are generated using Monte Carlo

simulations, and all these statistics are plotted to draw

an Efficient Frontier. Moreover, the portfolio

combinations with the highest Sharpe Ratio, highest

return and lowest volatility are specially marked on

the figure. Next, the portfolio is focused on a micro

view, using the Solver technique in Excel to achieve

the objective function. CML and Efficient Frontier

are plotted, and the tangent point was found to figure

out the weight allocation of the portfolio with the

maximum Sharpe Ratio. Tables and the NAV curve

are provided with explanations, and some investing

insights are given to different investors according to

their personal preferences. The lack of long-term data

and too much reliance on historical data are the

limitations of this paper. Further progress in

forecasting more reliable and accurate predictions

could be made as prospects on novel portfolios.

REFERENCES

Baker, M., McClain, T., 2019. Green bonds and the

economics of the green advantage. Finance Research

Letters, 29, 258-262.

Baur, D. G., Lucey, B. M., 2010. Is gold a hedge or a safe

haven? An analysis of stocks, bonds, and gold.

Financial Review, 45(2), 217-229.

Friede, G., Busch, T., Bassen, A., 2015. ESG and financial

performance: Aggregated evidence from more than

2000 empirical studies. Journal of Sustainable Finance

& Investment, 5(4), 210-233.

Glasserman, P., 2003. Monte Carlo methods in financial

engineering. Springer.

Gorton, G., Rouwenhorst, K. G., 2006. Facts and fantasies

about commodity futures. Financial Analysts Journal,

62(2), 47-68.

Jorion, P., 1997. Value at Risk: The new Benchmark for

Managing Financial Risk. McGraw-Hill.

Kearns, M., Nevmyvaka, Y., 2013. Machine learning for

market microstructure and high-frequency trading. Big

Data, 1(2), 160-167.

Litterman, R., 1990. Forecasting with Bayesian vector

autoregressions—five years of experience. Journal of

Business & Economic Statistics, 8(1), 25-38.

Markowitz, H., 1952. Portfolio selection. The Journal of

Finance, 7(1), 77-91.

Markowitz, H. 1959. Portfolio selection: Efficient

diversification of investments. Yale University Press.

Roy, A. D., 1952. Safety first and the holding of assets.

Econometrica, 20(3), 431-449.

Sharpe, W. F., 1964. Capital asset prices: A theory of

market equilibrium under conditions of risk. Journal of

Finance, 19(3), 425-442.

Yahoo Finance - Business Finance, Stock Market, Quotes,

News. (2024). Yahoo Finance.

https://finance.yahoo.com

Construction of Novel Portfolio Based on Modern Portfolio Theory

495