Novel Portfolio Construction Based on ESG

Yixuan Zhang

Department of Finance, Wenzhou-Kean University, Wenzhou, China

Keywords: ESG Factors, Portfolio Optimization, Multi-Factorial Model.

Abstract: As global financial markets continue to grow increasingly complex, and as investors place greater emphasis

on sustainable development, the limitations of traditional portfolio theory are becoming more evident. With

this in mind, this study examines the impact of incorporating ESG (i.e., Environmental, Social, and

Governance) factors into traditional multi-factor models on portfolio optimization, selecting eight stocks from

different industries over the period of 2021-2024 as research subjects. By conducting an empirical analysis,

the paper assesses the performance of portfolios with ESG factors across varying risk levels and contrasts

these with portfolios based on traditional multi-factor models. According to the analysis, the inclusion of ESG

factors leads to a significant enhancement in portfolio returns at different risk levels, particularly under high-

risk conditions, where ESG factors demonstrate strong capabilities in improving risk-adjusted returns. These

results provide valuable empirical support for the integration of ESG factors into modern portfolio

optimization, offering fresh insights for the advancement of sustainable investment strategies.

1 INTRODUCTION

The development of portfolio theory has undergone

several critical stages, laying the foundation for

modern finance. In 1952, Harry Markowitz

introduced Modern Portfolio Theory (MPT), which

marked the beginning of a scientific approach to asset

management by optimizing the balance between risk

and return through diversification (Markowitz, 1952).

Following this, in 1964, William Sharpe proposed the

Capital Asset Pricing Model (CAPM), which

incorporated market risk into portfolio optimization,

further enriching asset pricing theory (Sharpe, 1964).

During the 1970s, Eugene Fama's Efficient Market

Hypothesis (EMH) promoted the growth of index

investing, allowing investors to achieve long-term

returns by holding market indices (Fama, 1970). In

the 1980s and 1990s, the derivatives market expanded

rapidly, especially with the introduction of the Black-

Scholes option pricing model, which facilitated the

inclusion of futures, options, and other tools in

portfolio construction (Black, 1973). These

traditional portfolio theories assumed market

efficiency, investor rationality, and normally

distributed asset returns, providing a fundamental

framework for asset management. However, as

financial markets became more complex and

globalized, the limitations of these traditional theories

became increasingly evident in practice. Firstly,

traditional theories assumed that asset returns follow

a normal distribution, but real market performance

often deviates from this assumption (Mandelbrot,

1863). Secondly, in modern financial markets,

investors face increasing uncertainty, especially

during extreme events such as global financial crises,

where relying solely on traditional mean-variance

models is insufficient for effectively mitigating risk

(Taleb, 2007). Consequently, both academia and

industry have increasingly recognized the need to

incorporate additional dimensions into traditional

portfolio theory to better adapt to modern market

conditions (Lo, 2004).

Currently, portfolio theory is evolving with the

introduction of emerging asset classes and

advancements in technology, gradually overcoming

the limitations of traditional theories.

Cryptocurrencies, particularly Bitcoin, have been

widely recognized for their potential to enhance

portfolio diversification due to their high volatility

and low correlation with traditional assets (Brière et

al., 2015). Research indicates that incorporating

cryptocurrencies into traditional stock and bond

portfolios can significantly improve overall

performance, particularly in terms of risk

management. Further empirical analysis suggests that

cryptocurrencies may serve as a safe-haven asset

484

Zhang, Y.

Novel Portfolio Construction Based on ESG.

DOI: 10.5220/0013269200004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 484-490

ISBN: 978-989-758-726-9

under certain market conditions, though their high

volatility necessitates caution in practical

applications (Corbet et al., 2018). Additionally,

private equity, hedge funds, and real estate have

increasingly become vital tools for diversifying

investment portfolios over the past few years (Anson,

2007; Stulz, 2007). These asset classes have a low

correlation with traditional stocks and bonds,

enabling them to offer more stable returns during

market fluctuations. Studies have shown that

including these alternative investments in a portfolio

often significantly reduces overall volatility while

enhancing long-term returns (Pedersen et al., 2014).

This trend further underscores the need for traditional

portfolio theory to adapt to modern market conditions

by incorporating emerging asset classes and

addressing the complexities of financial markets

(Ang, 2014). In this context, traditional quantitative

investment strategies continue to play a crucial role.

These strategies rely on a series of quantifiable

factors that can predict the future performance of

stocks. The most common factors include momentum,

value, and quality factors. With the growing global

focus on sustainable development, the application of

ESG (Environmental, Social, and Governance)

factors in investments has also been increasing. The

use of ESG factors is no longer limited to socially

responsible investing but is gradually becoming a key

consideration for mainstream investors. Research

indicates that companies with high ESG ratings tend

to perform more steadily over the long term and can

effectively reduce portfolio risk. Moreover, ESG

factors can help investors avoid potential

environmental and social risks, thereby improving

risk-adjusted returns in their portfolios. However,

despite the increasing importance of ESG factors,

their integration into traditional investment strategies

remains contentious and under-researched. In recent

years, more studies have begun to explore how ESG

factors can be combined with traditional quantitative

factors to build more comprehensive multi-factor

models. For example, research has shown that

integrating ESG factors with momentum, value, and

quality factors can significantly enhance portfolio

performance and reduce investment risk. Some

studies have also highlighted that ESG factors

perform particularly well during economic downturns,

providing investors with a certain degree of downside

protection. Nevertheless, existing research has some

limitations. Many studies focus only on single

markets or short-term performance, lacking analysis

of long-term and cross-market effects. Additionally,

there is limited research on how to prioritize ESG

factors relative to traditional factors within multi-

factor models.

The paper aims to construct an innovative

portfolio optimization framework by integrating ESG

factors with traditional Alpha factors, thereby

developing a multi-factor model. Through empirical

analysis, the paper seeks to validate the effectiveness

of this model in achieving a balance between

maximizing financial returns and minimizing risk. By

incorporating ESG factors into the traditional multi-

factor model, the paper aims to optimize stock

selection and trading strategies, creatively combining

environmental, social, and governance (ESG)

dimensions with momentum, value, and quality

Alpha factors. In terms of data processing, the paper

will utilize stock and ESG rating data, coupled with

empirical analysis, to assess the model's performance

across different market environments and to verify its

robustness in multi-asset portfolios. Ultimately, the

paper aims to provide a comprehensive investment

solution that combines financial performance with

sustainable development goals, thereby promoting

the practical application of ESG investing.

2 DATA AND METHOD

The paper selected weekly price data from the past

three years for eight stocks, analysing them to

construct an investment portfolio. The data is based

on their market performance, ESG ratings, and

various factors such as momentum, value, and quality.

The eight selected stocks demonstrate strong ESG

performance and financial stability, and include

Microsoft, Costco, Adobe, NVIDIA, Apple, Walmart,

Johnson & Johnson, and Procter & Gamble, covering

multiple industries to ensure diversity and

representativeness in the portfolio.

ESG factors have increasingly gained importance

in the investment field as key indicators for assessing

a company's sustainable development capabilities.

ESG factors are divided into three components:

environmental factors, which focus on a company’s

performance in areas such as climate change and

resource utilization; social factors, which relate to

labor rights, community impact, and other social

considerations; and governance factors, which

examine a company’s management structure and

corporate ethics. By evaluating these factors,

investors can identify companies that are stable and

low risk over the long term. The inclusion of ESG

factors not only helps enhance the sustainability of

the investment portfolio but also serves as an

effective risk management tool. Typically, ESG

Novel Portfolio Construction Based on ESG

485

ratings are categorized into high, medium, and low

tiers, allowing investors to optimize their portfolios

by selecting companies that excel across these areas.

Furthermore, integrating ESG factors into a multi-

factor investment model can help balance returns and

risks amid market fluctuations, contributing to long-

term returns.

The Alpha factor model is a financial model used

in portfolio management and stock selection. It aims

to identify specific factors (Alpha factors) that can

explain and predict asset returns, thereby achieving

excess returns beyond the market benchmark. Alpha

factors represent the performance of individual stocks

or assets that are independent of the overall market

trend, i.e., the excess returns generated by active

management. By capturing the impact of these factors,

the model provides a basis for informed investment

decisions.

The paper selected three factors: momentum,

value, and quality. The momentum factor is based on

the historical price trends of assets, typically

reflecting the continuation of upward or downward

price movements. For the momentum factor, the

cumulative return over the past 12 months was used.

The value factor measures the pricing of an asset

relative to its fundamental value, with the price-to-

earnings ratio (P/E) being chosen to identify

undervalued or overvalued stocks. The quality factor

assesses a company's financial health and operational

efficiency, with return on equity (ROE) being

selected to identify high-quality companies. Each

factor may carry different weights depending on the

period and market conditions. The traditional multi-

factor model is:

𝑅



𝛼𝛽



𝑀𝑜𝑚𝑒𝑛𝑡𝑢𝑚𝛽



 𝑉𝑎𝑙𝑢𝑒 

𝛽



𝑄𝑢𝑎𝑙𝑖𝑡𝑦𝜖 (1)

In the traditional multi-factor model, an ESG factor is

introduced to adjust the portfolio's weight distribution.

The inclusion of the ESG factor may influence the

final portfolio selection, particularly in the analysis of

risk-adjusted returns. The multi-factor model with the

ESG factor is:

𝑅



𝛼𝛽



𝑀𝑜𝑚𝑒𝑛𝑡𝑢𝑚𝛽



 𝑉𝑎𝑙𝑢𝑒 

𝛽



𝑄𝑢𝑎𝑙𝑖𝑡𝑦𝛽



𝐸𝑆𝐺 (2)

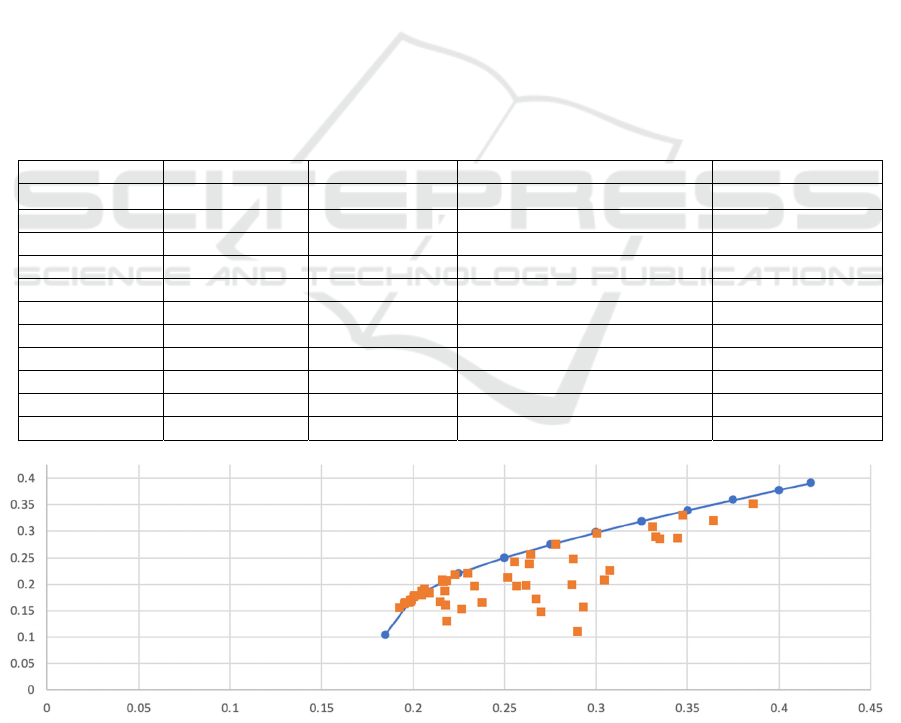
Table 1: Construction of effective frontier of traditional multi-factor model.

COST ADBE NVDA Portfolio standard deviation Portfolio return

0.8986 0.2833 -0.1819 0.1849 0.1046

0.8766 0.0614 0.0620 0.2000 0.1750

0.7564 0.0000 0.2436 0.2250 0.2202

0.6243 0.0000 0.3757 0.2500 0.2500

0.5135 0.0000 0.4865 0.2750 0.2750

0.4131 0.0000 0.5869 0.3000 0.2976

0.3191 0.0000 0.6809 0.3250 0.3188

0.2291 0.0000 0.7709 0.3500 0.3391

0.1422 0.0000 0.8578 0.3750 0.3587

0.0574 0.0000 0.9426 0.4000 0.3778

0.0000 0.0000 1.0000 0.4172 0.3908

Figure 1: The effective frontier of traditional multi-factor model (Photo/Picture credit: Original).

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

486

3 RESULTS AND DISCUSSION

3.1 Effective Frontier

After calculating the weighted average for each stock

(listed in Table 1), the paper determined the overall

scores for each stock, integrating the weights of

momentum, value, quality, and ESG factors. Based

on these scores, the top three stocks were selected to

construct the investment portfolio. Specifically, the

Figure. 1 (traditional multi-factor model) illustrates

the efficient frontier for Tesla (TSLA), Adobe

(ADBE), and Nvidia (NVDA). The efficient frontier

represents the optimal expected returns that investors

can achieve at different levels of risk. In this model,

the distribution of points is relatively tight, indicating

a stable and linear relationship between risk and

return. The risk range is mainly concentrated within a

portfolio standard deviation of 0.18 to 0.41, reflecting

a conservative level of risk. The return at low-risk

levels is relatively modest, and the increase in returns

is gradual, suggesting that in the traditional multi-

factor model, higher expected returns typically

require taking on greater risk.

The Figure. 2 shows the efficient frontier after

incorporating the ESG factor, with the portfolio

comprising Adobe (ADBE), Nvidia (NVDA), and

Apple (AAPL), where the parameters are listed in

Table 2.. Compared to the traditional model, the

inclusion of the ESG factor significantly alters the

shape and position of the efficient frontier, shifting

the curve upward and to the left. This shift indicates

that investors can achieve higher expected returns at

the same level of risk. The range of points is broader,

particularly in the high-risk area, suggesting that the

ESG factor enables the model to better accommodate

diversified risk/return combinations. Compared to the

traditional model, the risk range under the ESG model

expands, with the standard deviation ranging from

0.2489 to 2.5, showing that this portfolio can tolerate

higher risk levels while also delivering substantially

higher returns. For example, at a standard deviation

of 0.35, the return can reach 0.6454, indicating that

high returns can still be achieved even at lower risk

levels. The maximum portfolio return increases

significantly from approximately 0.3907 in the

traditional model to 14.0475, with a corresponding

portfolio standard deviation also rising to 2.5,

indicating that investors can obtain greater returns

while accepting higher risks.

Table 2: Effective frontier construction of models incorporating ESG factors.

ADBE NVDA AAPL Portfolio standard deviation Portfolio return

0.8517 0.2194 -0.0710 0.2489 -0.8316

0.9972 0.0006 0.0023 0.3000 0.1280

0.8347 0.1287 0.0366 0.3500 0.6454

0.8295 0.1046 0.0659 0.4000 1.0481

0.8249 0.0821 0.0929 0.4500 1.4190

0.8203 0.0610 0.1186 0.5000 1.7717

0.8168 0.0397 0.1435 0.5500 2.1128

0.8148 0.0174 0.1678 0.6000 2.4459

0.7853 0.0000 0.2147 0.7000 3.0960

0.7398 0.0000 0.2602 0.8000 3.7315

0.6950 0.0000 0.3050 0.9000 4.3577

0.6506 0.0000 0.3494 1.0000 4.9776

0.6066 0.0000 0.3934 1.1000 5.5930

0.5628 0.0000 0.4372 1.2000 6.2051

0.5191 0.0000 0.4809 1.3000 6.8148

0.4756 0.0000 0.5244 1.4000 7.4225

0.4323 0.0000 0.5677 1.5000 8.0287

0.3890 0.0000 0.6110 1.6000 8.6337

0.3457 0.0000 0.6543 1.7000 9.2376

0.3026 0.0000 0.6974 1.8000 9.8407

0.2594 0.0000 0.7406 1.9000 10.4431

0.2164 0.0000 0.7836 2.0000 11.0449

0.1303 0.0000 0.8697 2.2000 12.2471

0.0015 0.0000 0.9985 2.5000 14.0475

Novel Portfolio Construction Based on ESG

487

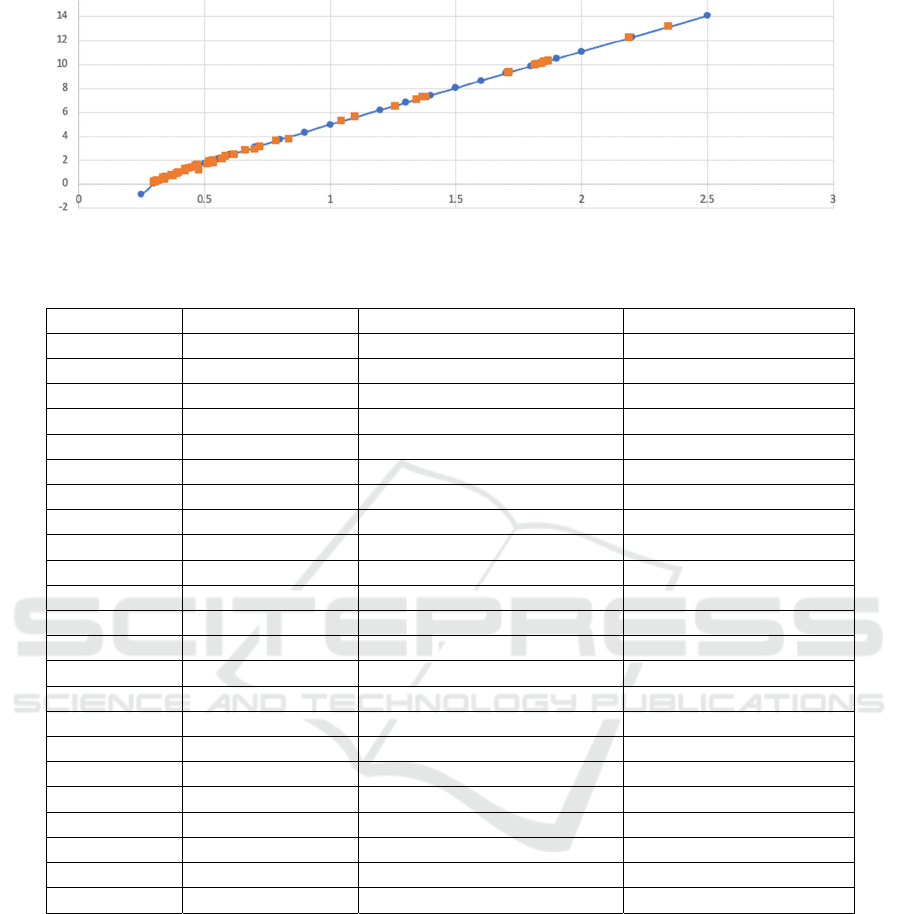
Figure 2: Effective frontier of model incorporating ESG factors (Photo/Picture credit: Original).

Table 3: Optimal risk combination of traditional multi-factor model.

COST ADBE NVDA

0.57154927 0 0.42845073

Rf Portfolio Rf+Portfolio standard deviation Rf+Portfolio return

-1 2 0.52302755 0.51398898

-0.9 1.9 0.49687617 0.48877611

-0.8 1.8 0.4707248 0.46356325

-0.7 1.7 0.44457342 0.43835038

-0.6 1.6 0.41842204 0.41313752

-0.5 1.5 0.39227066 0.38792465

-0.4 1.4 0.36611929 0.36271178

-0.3 1.3 0.33996791 0.33749892

-0.2 1.2 0.31381653 0.31228605

-0.1 1.1 0.28766515 0.28707318

0 1 0.26151378 0.26186032

0.1 0.9 0.2353624 0.23664745

0.2 0.8 0.20921102 0.21143459

0.3 0.7 0.18305964 0.18622172

0.4 0.6 0.15690827 0.16100885

0.5 0.5 0.13075689 0.13579599

0.6 0.4 0.10460551 0.11058312

0.7 0.3 0.07845413 0.08537025

0.8 0.2 0.05230276 0.06015739

0.9 0.1 0.02615138 0.03494452

1 0 0 0.00973166

3.2 Model Performance

In the first set of results, one can clearly observe the

performance of the investment portfolio under

different optimization functions. The efficient

frontier demonstrates the optimal returns achievable

at various levels of risk. For instance, in the minimum

variance portfolio, the allocation tends to reduce

exposure to highly volatile stocks (such as NVDA) to

lower overall risk. This strategy effectively controls

the portfolio’s volatility, providing relatively stable

returns. In the maximum Sharpe ratio portfolio, more

weight is allocated to higher-returning stocks (such as

COST and NVDA) to maximize risk-adjusted returns.

This allocation strategy aims to enhance overall

portfolio returns, albeit potentially with higher

volatility. The optimal investment portfolio under the

traditional model exhibits lower standard deviation

and relatively stable returns, with the highest Sharpe

ratio recorded at 1.001325, indicating that the

portfolio can achieve solid performance under strict

risk control. Additionally, this suggests that the

traditional factor model is already capable of

balancing returns and risks to some extent, though its

potential for improvement is limited. The results are

listed in Table 3.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

488

Compared to the traditional model, the efficient

frontier curve after incorporating the ESG factor is

steeper, indicating that as investors are willing to take

on more risk, the rate of return increases more

significantly. The ESG-enhanced model

demonstrates stronger risk tolerance, allowing for

optimized investment returns across a broader range

of risk levels. Although the risk level increases, the

portfolio’s returns also rise considerably, reflecting

the effectiveness of the ESG factor in portfolio

optimization. Notably, the Sharpe ratio significantly

improves after the inclusion of the ESG factor,

reaching a maximum of 5.619526. This substantial

increase indicates that the ESG factor not only

enhances portfolio returns but also significantly

optimizes risk-adjusted returns, allowing investors to

achieve markedly higher returns at the same level of

risk. Furthermore, the optimal investment portfolio

under the ESG model performs exceptionally well

under high-risk conditions, particularly when the risk-

free rate is set at 1.0, with a return of 14.06808, far

surpassing the performance under the traditional

model. This demonstrates that the ESG factor not

only boosts the return potential of the portfolio but

also offers more attractive returns under high-risk

conditions, proving its critical role in long-term

investment strategies. The results are shown in Table

3.3 Explanation and Implications

When comparing the traditional multi-factor

model with the model incorporating ESG factors, it is

evident that the inclusion of ESG factors significantly

enhances portfolio performance, particularly under

high-risk conditions. The steeper efficient frontier

observed after adding ESG factors indicates that as

risk increases, the rate of return improves more

markedly, highlighting the crucial role of ESG factors

in boosting portfolio return potential. Additionally,

the ESG factors significantly increase the portfolio's

Sharpe ratio, demonstrating a substantial contribution

to risk-adjusted returns. These results suggest that

Table 4: Optimal risk mix of models with ESG factors.

ADBE NVDA AAPL

0 0 1

Rf Portfolio Rf+Portfolio standard deviation Rf+Portfolio return

-1 2 5.006857804 28.12643346

-0.9 1.9 4.756514914 26.72059837

-0.8 1.8 4.506172024 25.31476328

-0.7 1.7 4.255829133 23.90892819

-0.6 1.6 4.005486243 22.5030931

-0.5 1.5 3.755143353 21.09725801

-0.4 1.4 3.504800463 19.69142292

-0.3 1.3 3.254457573 18.28558783

-0.2 1.2 3.004114682 16.87975274

-0.1 1.1 2.753771792 15.47391765

0 1 2.503428902 14.06808256

0.1 0.9 2.253086012 12.66224747

0.2 0.8 2.002743122 11.25641238

0.3 0.7 1.752400231 9.850577288

0.4 0.6 1.502057341 8.444742197

0.5 0.5 1.251714451 7.038907107

0.6 0.4 1.001371561 5.633072017

0.7 0.3 0.751028671 4.227236926

0.8 0.2 0.50068578 2.821401836

0.9 0.1 0.25034289 1.415566746

1 0 0 0.009731655

Novel Portfolio Construction Based on ESG

489

integrating ESG factors into long-term investment

strategies can not only optimize risk management but

also lead to more substantial returns. Even if the

selected stocks are similar or the same, the inclusion

of ESG factors may improve risk-adjusted returns,

offering valuable insights for adjusting future

investment strategies. This analysis can assist

investors in developing more robust and sustainable

investment portfolios in the modern market

environment. Furthermore, ESG factors provide

greater portfolio diversification, enabling investors to

adapt strategies flexibly in various market conditions,

further enhancing the stability and sustainability of

investments.

3.4 Limitations and Prospects

Despite the significant improvement in portfolio

performance achieved through the incorporation of

ESG factors, this paper has some limitations. Firstly,

the time span of the data sample is limited and does

not cover longer market cycles, which may affect the

generalizability of the results. Secondly, the

assignment of weights to ESG factors is somewhat

subjective, and the paper does not deeply explore the

impact of different weight configurations on portfolio

performance. Additionally, this research focuses on a

small number of stocks, which limits the applicability

of the findings across different markets and industries.

Future research should consider expanding the

sample to include a broader range of market cycles

and asset classes, while also employing more

dynamic weight adjustment mechanisms to enhance

the reliability and applicability of the results.

Furthermore, exploring the integration of ESG factors

with other emerging factors, such as big data and

artificial intelligence, could provide additional

perspectives and innovative opportunities for

portfolio optimization.

4 CONCLUSIONS

To sum up, this study significantly advances the

traditional multi-factor model by integrating ESG

factors, thereby developing a more forward-looking

and adaptable framework for portfolio optimization.

The research findings indicate that the inclusion of

ESG factors not only boosts portfolio returns across

various risk levels but also exhibits particularly strong

performance under high-risk conditions, showcasing

substantial risk-adjusted return capabilities.

Moreover, the paper highlights that the integration of

ESG factors effectively enhances the portfolio's

Sharpe ratio, further optimizing the overall

investment performance. Despite these promising

results, the research is constrained by a limited time

span and a small sample of stocks, which may affect

the broader applicability of the findings. Future

research could address these limitations by expanding

the sample size, utilizing dynamic factor weight

adjustments, and incorporating other emerging

factors to improve the generalizability and robustness

of the results. Overall, this paper provides critical

empirical support for incorporating ESG factors into

modern portfolio optimization strategies,

contributing to the advancement of sustainable

investment practices.

REFERENCES

Ang, A. 2014. Asset Management: A Systematic approach

to factor investing. OUP Catalogue.

Anson, M., 2007. Performance Measurement in Private

Equity: Another Look. The Journal of Private Equity,

103, 7–21.

Black, F., Scholes, M., 1973. The Pricing of Options and

Corporate Liabilities. Journal of Political Economy,

813, 637–654.

Brière, M., Oosterlinck, K., Szafarz, A., 2015. Virtual

currency, tangible return: Portfolio diversification with

bitcoin. Journal of Asset Management, 166, 365–373.

Corbet, S., Meegan, A., Larkin, C., Lucey, B., Yarovaya, L.,

2018. Exploring the dynamic relationships between

cryptocurrencies and other financial assets. Economics

Letters, 165, 28–34.

Fama, E. F., 1970. Efficient Capital Markets: A Review of

Theory and Empirical Work. The Journal of Finance,

252, 383–417.

Lo, A. W. 2004., The Adaptive Markets hypothesis. The

Journal of Portfolio Management, 305, 15–29.

Mandelbrot, B., 1963. The Variation of Certain Speculative

Prices. The Journal of Business, 364, 394–419.

Markowitz, H., 1952. Portfolio Selection. The Journal of

Finance, 71, 77–91.

Pedersen, N., Page, S., He, F., 2014. Asset Allocation: Risk

Models for Alternative Investments. Financial Analysts

Journal, 703, 34–45.

Sharpe, W. F., 1964. Capital Asset Prices: A Theory of

Market Equilibrium under Conditions of Risk. The

Journal of Finance, 193, 425–442.

Stulz, R. M., 2007. Hedge Funds: Past, Present, and Future.

The Journal of Economic Perspectives, 212, 175–194.

Taleb, N. N., 2007. Black Swans and the Domains of

Statistics. The American Statistician, 613, 198–200.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

490