Portfolio Design and Optimization Based on the CAPM Model

Boxiong Xing

International Business School, Xi'an Jiaotong-Liverpool University, Suzhou, China

Keywords: Portfolio Optimization, Asset Allocation, Risk Management, Capital Asset Pricing Model (CAPM),

Conditional Value at Risk (CVaR).

Abstract: In the evolving landscape of global financial markets, traditional portfolio management approaches face

challenges due to the rise of new asset classes and increasingly complex investment environments. This study

examines the optimization of portfolio returns and risks by integrating traditional assets with emerging ones.

This paper explores the optimization of portfolio returns and risks by combining traditional and emerging

assets. The research uses data from assets (e.g., Apple, crude oil, Bitcoin, and SPY options), employing

models including CAPM, the mean-variance model, and CVaR to determine the most efficient asset allocation.

The results reveal that a portfolio consisting of 50% Apple, 10% crude oil, 30% SPY, and 10% Bitcoin

achieves an expected annualized return of 8.32% with an annualized volatility of 8.46%. This allocation

achieves a strong balance between risk and return, offering a solid foundation for optimizing portfolio

strategies. This research highlights the significance of strategic asset allocation and sophisticated risk

management, offering key insights for investors aiming for stable, long-term growth. Future research could

further improve portfolio performance by incorporating real-time data and machine learning models, allowing

for more adaptive and responsive investment strategies in the face of market uncertainties.

1 INTRODUCTION

Investors in the world's financial markets with a little

bit of investment philosophy put their core focus on

the asset allocation and portfolio management part of

the equation (Fama & French, 2004; Jagannathan &

McGrattan, 1995). Traditional theories of financial

markets and traditional investment assets such as

stocks have always been the mainstay of the

investment market. Recent developments in the world

have brought with them a diversification of financial

instruments and ever closer international market

relations. Modern asset portfolio theory (MPT) and

capital asset pricing models have also begun to be

gradually applied, but they have encountered certain

limitations in dealing with the emergence of new

asset classes and the complexity of the contemporary

market environment (Markowitz, 1991). More

recently, the growth of new asset classes, such as

cryptocurrencies and futures, and their inclusion in

investment portfolios have further raised questions

about the applicability of these traditional financial

theories. MPT offers a theoretical framework for

asset allocation, primarily through mean-variance

optimization. However, this theory hinges on the

assumptions of normally distributed asset returns and

a stable covariance matrix, which may not hold true

in markets characterized by non-linearity and extreme

volatility. To address these shortcomings, the CAPM

model was introduced, which evaluates the

systematic risk and anticipated return of individual

assets. Nevertheless, as market complexity escalates,

particularly with the incorporation of new assets like

cryptocurrencies and futures, traditional models like

CAPM are increasingly challenged by issues such as

non-linear data and the need for advanced risk

management strategies.

In response to these challenges, researchers have

developed several enhanced models and approaches,

including the CVaR model and genetic algorithms.

These innovations seek to address the shortcomings

of traditional CAPM. For example, the CVaR model

provides a more comprehensive risk management

strategy by considering tail risks in extreme market

conditions, while genetic algorithms excel in

handling complex, non-linear optimization

challenges.

The objective of this research is to investigate and

assess how to optimize portfolio returns and risks by

integrating various models within portfolios that

Xing, B.

Portfolio Design and Optimization Based on the CAPM Model.

DOI: 10.5220/0013268900004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 469-475

ISBN: 978-989-758-726-9

469

combine both traditional and emerging assets. With

the rise of new assets (e.g., cryptocurrencies),

traditional portfolio theory can no longer fully meet

the needs of modern investors. Thus, by incorporating

advanced tools such as the CAPM, the mean-variance

model, and the CVaR model, this study aims to offer

new insights and approaches for portfolio

optimization both in theory and practice.

The study begins with a comprehensive literature

review, examining research on portfolios containing

both traditional and emerging assets, analysing their

theoretical underpinnings and practical limitations.

Following this, the data sources and methodologies

employed are detailed, including the specific

application and computational processes of each

model. The study then proceeds to an empirical

analysis to evaluate the performance of these models

in portfolio optimization, discussing their validity and

any limitations encountered. The findings are

ultimately summarized, with recommendations and

directions for future research provided.

2 DATA AND METHOD

The data sources for this study cover a number of

important financial markets and trading platforms,

and the time span for data selection is from August 1,

2019 to August 1, 2024, a total of five years. The data

are presented on a weekly basis to ensure data

diversity and accuracy. Specifically:, for legacy asset

Apple Inc (APPL) Stock Data: daily closing prices,

trading volume, and other relevant data for Apple Inc

stock are obtained through Yahoo Finance. A five-

year time horizon provides ample historical data for

yield and volatility analysis. For WTI Crude Oil

Futures Data. The daily price data from CME Group.

WTI crude oil futures, as the most critical energy

commodity globally, are utilized to evaluate how

fluctuations in the energy market influence

investment portfolios. For emerging asset, Bitcoin

(BTC) Data used daily closing price and volume data

for Bitcoin via CoinMarketCap. A recent five-year

time horizon was chosen to reflect the long-term

trends and volatility of the Bitcoin market. SPY

Options data collected from Yahoo Finance, covering

a variety of strike price and expiration date data for

S&P 500 ETF (SPY) options. This data is used for

risk management and yield optimization. This data

will be used to construct a diversified portfolio

containing both traditional and emerging assets. The

underlying assets are selected based on their market

impact, liquidity, and risk-return characteristics. By

introducing these assets, the study can analyze the

synergies between different asset classes and their

impact on overall portfolio risk and return.

When conducting portfolio optimization, the

selection of the objective function is vital, as it

significantly influences risk-reward trade-offs the

optimization process. The study uses the following

objective functions to evaluate and optimize the

portfolio:

 Maximize Sharpe ratio. The objective of this

study is to optimize the Sharpe ratio in order to

identify the portfolio with the highest return for

a given level of risk. The Sharpe ratio is a risk-

adjusted return measure that compares an asset's

excess return to its volatility.

 Minimizing Risk (Variance). Risk minimization

is one of the core objectives of modern portfolio

theory. This study will create a low-risk

portfolio by focusing on minimizing the

portfolio's variance. This method is particularly

well-suited for conservative investors, aiming to

mitigate the effects of asset price fluctuations on

the portfolio.

 Minimizing Conditional Value at Risk (CVaR).

CVaR is an important metric used to assess the

maximum loss under extreme market conditions.

By minimizing CVaR, this study will construct

portfolios that are less risky under extreme

market conditions, which is especially

important for portfolios that contain highly

volatile assets such as Bitcoin.

 Maximize Return (Expected Return). In some

cases, investors may be more concerned with

the expected return of a portfolio. By

maximizing expected returns, this study will

evaluate the performance of high-yield

portfolios in different market environments for

aggressive investment strategies.

These objective functions will be applied in

different models and methods, and optimization

analysis will be performed by tools such as CAPM,

mean-variance model and CVaR model. Through

these optimization methods, this study will explore

the optimal portfolio construction strategies and their

effects under different investment objectives.

In analyzing asset returns, this study uses the

symbols and definitions displayed in Table 1. The

specific definitions and units of these symbols are

listed in Table 1 for easy understanding and use.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

470

Table 1: Symbol description.

Notation Meanin

𝑖 Asset

𝐸



𝑅





Expected rate of return on asset 𝑖

𝑅



Risk − free rate

𝛽



𝛽 − coefficient for asset 𝑖

𝐸



𝑅





Expected return on the market portfol

𝑅



Rate of return on assets

𝑅



Market rate of return

𝑃



Closing price of the index in week 𝑡

𝑉𝑎𝑟



𝑅





Variance of market returns

In this study, data were collected for four assets:

shares of Apple Inc (APPL), Crude Oil WTI Futures,

S&P 500 ETF (SPY), and Bitcoin. Please refer to

Appendix 1 for the specific data. In order to guarantee

the accuracy of the data and the uniformity of the

analysis, the following preprocessing steps were

undertaken. First, the raw data was imported from

various data sources, and relevant information such

as Time (Date), Close and Volume were extracted,

and other irrelevant columns were removed. For each

asset data, the column names were standardized as

Date, Close and Volume to facilitate subsequent data

integration. The datasets for each asset were merged

(outer join) by date (Date). During the merging

process, it was ensured that all the data had the same

time range and were aligned by Date. The resulting

integrated data frame contains the closing price and

trading volume for each asset on the same date. A

small number of missing values appear in the merged

data frame due to possible differences in trading times

across assets. To fill in these missing values, a

stepwise interpolation method is used. The missing

data are first filled using the forward fill (pad) method,

followed by applying the backfill method to the

portions where missing values still exist, ensuring

data integrity. To be able to reasonably compare the

performance of different assets, the closing prices of

each asset are normalized using the Min-Max

normalization method. The standardized data

converts the closing prices of each asset into the range

of [0, 1] so that they can be compared and analyzed

on the same scale. The above preprocessing steps

result in a complete and standardized dataset that can

support subsequent analysis and research. Please refer

to Appendix 2 for details.

For model assumption, it is assumed that the

market operates efficiently, with all available

information already incorporated into asset prices, so

that there is no systematic information advantage.

Assets are priced rationally, and investors cannot

obtain excess returns through information asymmetry.

The study assumes that market conditions are

relatively stable over the study period, with no major

structural changes or sudden systemic risks. This

implies that historical data is effective in predicting

future market behavior and that the risk and return

characteristics of assets remain constant over the

study period. If the asset's returns are normally

distributed, the mean-variance optimization method

can be applied. While returns may occasionally

exhibit fat tails or skewness, this model assumes a

normal distribution for simplicity. It is assumed that

the correlation between different assets remains

constant and exhibits minimal variation over time. As

a result, the correlation parameters within the

covariance matrix stay unchanged throughout the

study. The study presumes that no transaction costs or

tax liabilities are involved in portfolio adjustments,

enabling investors to modify their asset allocation

without the influence of transaction fees. The

assumption of rational investor behavior: It is

assumed that all investors are rational and that their

investment decisions are based on an analysis of risk

and return aimed at maximizing their utility function.

This assumption excludes the impact of investor

behavioral biases on market prices and portfolios.

3 RESULTS AND DISCUSSION

3.1 Calculation of Basic Indicators

To comprehensively evaluate the risk and return

features of various assets, one computed and

examined key financial metrics across several assets.

Table 2: Data preprocessing results

Annualized

mean return

Annualized

variance

Annualized

volatilit

Sharpe ratio Maximum

retracement

CVaR (95%)

APPL -4.74524 34.32520 5.85877 -0.809939 1.99435 -0.83951

Crude Oil WTI

Futures Historica

13.75573 413.13013 20.32560 0.67676 36.32113 -0.75141

SPY -13.17218 546.78701 23.38347 -0.56331 2.92006 -1.46487

Bitcoin 3.09303 25.18650 5.01861 0.61631 3.30931 -0.54200

Portfolio Design and Optimization Based on the CAPM Model

471

Specifically, the following measures were calculated:

 Annualized mean return: Calculates the

annualized average return for each asset,

highlighting its performance over time.

 Annualized variance: The risk level is

determined by evaluating the fluctuations in

asset returns.

 Annualized volatility: As a measure of risk,

denotes the standard deviation of return

volatility.

 Sharpe ratio: Measure the performance of

returns at the same level of risk under the

assumption that the risk-free rate is 0%.

 Maximum retracement: An assessment of the

maximum loss experienced by the asset during

a retracement, showing the potential downside

risk to the asset.

 CVaR (95%)：Assesses potential losses under

extreme market conditions to further

characterize risk.

By computing and evaluating these metrics, one

can gain a broader insight into the performance of

each asset and establish a foundation for future

investment decisions. Specific charts are shown in

Table 2.

3.2 CAPM Modelling

The CAPM is a commonly employed tool in finance

to assess the anticipated return of an individual asset

or portfolio. It calculates the expected return by

incorporating the market risk premium and connects

the asset's systematic risk (beta) to the broader

market's volatility. The fundamental principle of the

CAPM is to assess an asset's exposure to market risk

using the beta coefficient and subsequently calculate

a fair expected return. In this study, the CAPM serve

as a tool to analyze the potential losses that could be

incurred by you in the market of individual assets and

provide basic data for subsequent portfolio

optimization. The CAPM model exhibits different

validity under different market conditions, which is

reflected in the results of this paper (Fama & French,

2004). To construct the CAPM model, this study uses

weekly data for the past five years, including

historical weekly return data for several assets,

including Apple (APPL), WTI crude oil futures, SPY

options, and Bitcoin (BTC). The historical returns of

the market portfolio are represented using the S&P

500 index (S&P 500).

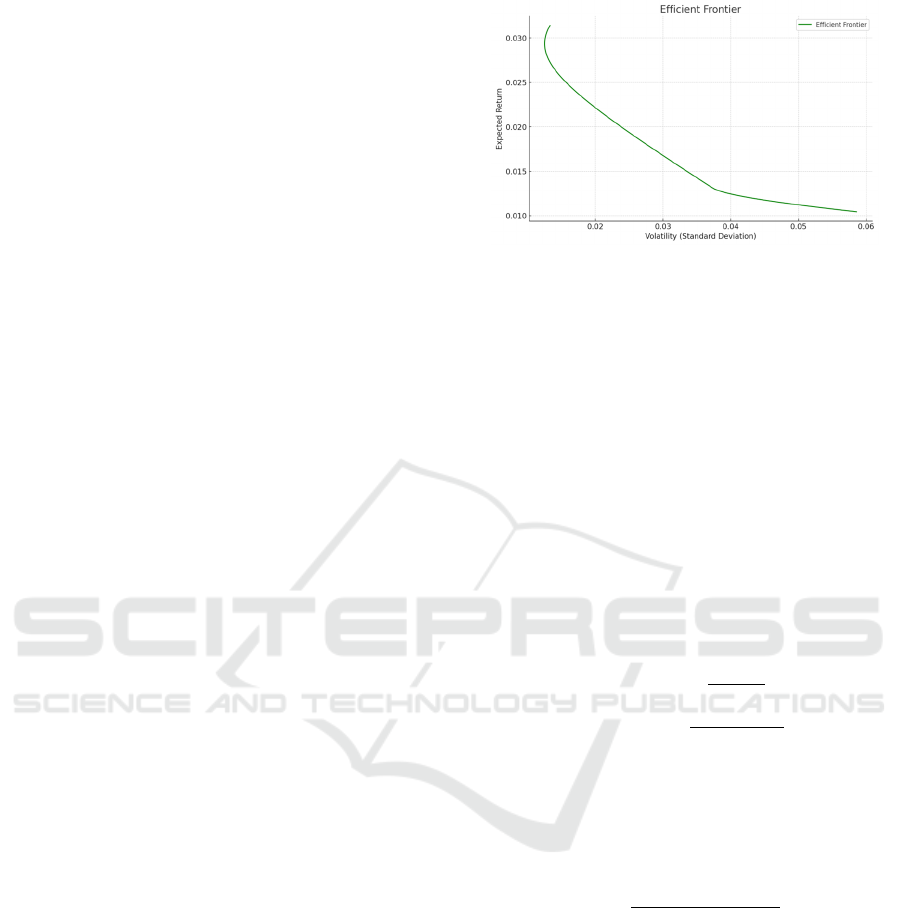
Figure 1: Effective Frontier (Photo/Picture credit:

Original).

A 4.61% risk-free rate was selected, derived from

the current yield on the 10-year U.S. Treasury bond,

as shown in Appendix 3. In the CAPM model, the

risk-free rate serves as a reference return,

representing the minimum return investors would

anticipate in the absence of market risk. Fig. 1

illustrates the portfolio's expected return across

various risk levels.

The beta coefficient is utilized to assess an asset's

systematic risk, reflecting its sensitivity to market-

wide fluctuations. To derive the beta coefficient, one

used historical S&P500 data from August 1, 2019, to

August 1, 2024, with the source detailed in Appendix

3. The calculated market volatility was 1.33%, and

the market's expected return was 3.14%:

𝑅

















(1)

𝜎















(2)

To assess the systematic risk of different assets

relative to the market, this study calculates the beta

coefficients of APPL, Crude Oil WTI Futures, SPY,

and Bitcoin. The beta coefficients were calculated

using the following formula:

𝛽

Cov







，















(3)

Table 3 shows the beta coefficients of the four

selected assets. The results show that APPL has a beta

of 1.184, indicating higher volatility than the market,

while Crude Oil WTI Futures has a beta of 0.897,

indicating lower volatility than the market, and SPY

and Bitcoin have a beta of 0.941 and 0.900,

respectively, indicating that the volatility of the two

is closer to the market.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

472

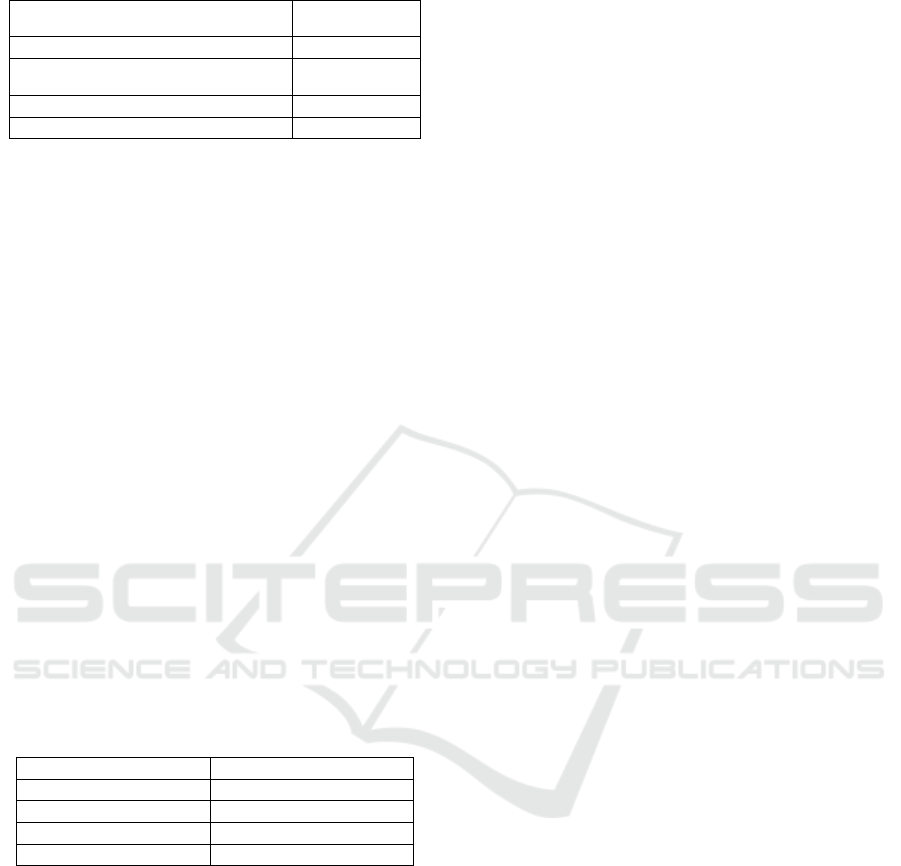
Table 3: The 𝛽 – coefficients.

Asset Beta

APPL 1.184

Crude Oil WTI Futures Historical 0.897

SPY 0.941

Bitcoin 0.9

This study uses the Capital Asset Pricing Model

(CAPM) to calculate the expected rate of return for

each asset.The formulae for the CAPM model are as

follows:

𝐸



𝑅





= 𝑅



+ 𝛽



× 𝐸



𝑅





− 𝑅



 (4)

Here, 𝐸



𝑅





is expected rate of return on asset 𝑖. 𝑅



is risk-free rate.𝛽 -coefficient for asset 𝑖，indicates

the systematic risk of the asset relative to the market。

𝐸



𝑅





is expected return on the market portfolio，

𝐸



𝑅





- 𝑅



is the market risk premium.

In the previous section, one calculated the market

return to be 3.14% and noted that the risk-free rate is

4.61%. Using the following formula, one derived a

risk premium of -1.77%. This indicates that the

expected market return is lower than the risk-free rate,

suggesting that investors believe the risk associated

with holding market assets (e.g., stocks) is not

sufficiently compensated and may even result in a

loss. Using the data above and the beta coefficients,

one applied the CAPM formula to compute the

annualized expected return for each asset. The results

of these calculations are presented in Table 4.

Table 4: Expected returns.

Asset Expected Return (%)

APPL 1.0443%

Crude Oil WTI Futures 1.5523%

SPY 1.4744%

Bitcoin 1.5470%

The analysis of the CAPM model indicates that an

asset's expected return is directly linked to its beta

coefficient, suggesting that a higher beta results in a

higher expected return. This outcome aligns with

financial theory, which posits that investors anticipate

greater returns when taking on higher systematic risk.

In this research, the market risk premium is negative,

indicating the current market's pessimistic outlook on

future returns. Under such market conditions, the

expected return derived from the CAPM model is

lower than the risk-free rate, implying that investors

might favor risk-free assets to mitigate market risk.

By calculating the beta coefficients of each asset,

the study reveals the differences in risk exposure of

different assets to market volatility. For assets with

high beta coefficients (e.g., APPL), they have higher

market risk and therefore higher expected returns.

While for assets with low beta coefficients (e.g.,

Crude Oil WTI Futures), their market risk is relatively

low and therefore the expected return is lower. By

utilizing the CAPM model, this study uncovers both

the expected return and market risk attributes of each

asset, laying a strong foundation for subsequent

portfolio optimization. Future research could

integrate the mean-variance optimization model to

delve deeper into constructing a risk-adjusted optimal

portfolio under prevailing market conditions.

3.3 Mean-variance Optimization Model

To maximize the expected return for a given level of

risk or minimize the risk for a given return target, this

study adopts Mean-Variance Optimization (MVO)

for portfolio optimization. Mean-Variance

Optimization is the core method of modern portfolio

theory, which helps investors construct optimal

portfolios by optimally allocating the weights of

different assets. The core concept of mean-variance

optimization is to maximize expected returns by

reducing the portfolio's variance Diversification

across multiple asset classes is effective in reducing

overall portfolio risk (Goetzmann et al., 2005). In

optimizing portfolios, this study aims to achieve an

optimal trade-off between risk and return by

employing a dual-objective strategy that focuses on

maximizing the Sharpe ratio while minimizing

volatility. However, a strategy based solely on Sharpe

ratio maximization often tends to concentrate on a

few high-return assets, resulting in an under-

diversified portfolio. Therefore, this study further

introduces diversification constraints to ensure that

the portfolio is reasonably allocated among different

assets.

To enhance portfolio diversification, minimum

weight and maximum weight constraints are set for

each asset in the study, i.e., the weight of each asset

in the portfolio should not be less than 10% and not

more than 50%. This constraint aims to prevent the

portfolio from being overly dependent on a single

asset and reduce concentration risk. The mean-

variance model, despite its widespread use, exhibits

limitations in dealing with nonlinear market behavior

(Elton et al., 2007). After optimization, the portfolio

weight allocation after considering the diversification

constraint is as shown in Table 5.

Portfolio Design and Optimization Based on the CAPM Model

473

Table 5: Portfolio weightings 1.

Asset Data

APPL 30%

Crude Oil WTI Futures 50%

SPY 10%

Bitcoin 10%

The optimization results show that under the

mandatory diversification constraint, the portfolio has

an expected return of 0.2385%, a volatility of 3.34%,

and a Sharpe Ratio of -1.399. Despite the low Sharpe

Ratio, the overall volatility is effectively controlled

due to the diversified allocation of the portfolio

among different assets. With the introduction of the

diversification constraint, the portfolio is no longer

concentrated in just a single asset but has a reasonable

allocation across multiple assets. While this

allocation reduces the Sharpe ratio, it improves the

stability of the portfolio and helps to reduce the

impact of extreme market volatility in long-term

investments. The choice of assets has some

limitations at the same time. Bitcoin is a decentralized

asset and can be highly volatile. Cryptocurrencies,

especially Bitcoin, are considered speculative assets

due to their high volatility (Baur et al., 2018).

Meanwhile, commodities such as crude oil are key

variables in investment portfolios due to their

volatility (Cheung & Miu, 2010). It is their

combination that makes this investment more

possible.

3.4 Risk Management Optimization

In portfolio management, an effective allocation of

asset weights is essential to strike a balance between

risk and return. As described by Rockafellar and

Uryasev (2000), CVaR models provide a more

reliable risk management tool under extreme market

conditions. To reduce the downside risk of the

portfolio in a volatile market environment, this study

optimizes the asset weights of four key assets by

incorporating two critical risk measures, Maximum

Drawdown (MDD) and Conditional Value at Risk

(CVaR). This paper analyzes the maximum

drawdown and CVaR data for four assets: Apple Inc.

stock (APPL), Crude Oil WTI Futures, S&P 500 ETF

(SPY), and Bitcoin. The initial weights are set to 30%

for Apple stock, 50% for WTI Crude Oil Futures, 10%

for SPY, and 10% for Bitcoin.

Effective risk management is key in financial

markets (Jorion, 2006). To prevent the portfolio from

being overly concentrated in any single asset and to

maintain a balanced allocation across assets, the study

imposes constraints, setting a minimum weight of 10%

and a maximum weight of 50% for each asset. This is

intended to optimize portfolio diversification while

controlling risk. In this study, an optimization method

based on the SLSQP (Sequential Least Squares

Programming) algorithm is used, with the objective

function being to minimize the weighted sum of the

portfolio's maximum retracement and CVaR. By

adjusting the weights of each asset, the optimal

portfolio allocation is obtained. In the weight

optimization process, the final optimal weight

allocation is given by considering the weight

constraints of at most 50% and at least 10% for each

asset as given in Table 6.

Following the optimization, the portfolio achieves

an annualized expected return of 8.32% and an

annualized volatility of 8.46%. This allocation

balances risk management and returns, enabling the

portfolio to perform more consistently across varying

market conditions. By incorporating weight

constraints in the optimization process, this study not

only achieves effective risk control, but also ensures

portfolio diversity. The optimized portfolio allocation

can strike a good balance between risk and return and

is suitable for investors seeking solid returns. Future

research can further explore the strategy of

dynamically adjusting weights under different market

environments to cope with more complex market

fluctuations.

Table 6: Portfolio weightings 2.

Asset Pro

ortion

APPL 50%

Crude Oil WTI Futures 10%

SPY 30%

Bitcoin 10%

3.5 Performance Indicators of the

Portfolio

Besides analyzing individual assets, the portfolio’s

overall performance was assessed using several key

financial indicators, including portfolio return,

Sharpe ratio, and Calmar ratio. Table 7 presents a

detailed overview of these indicators, offering

insights into the portfolio’s risk and return profile.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

474

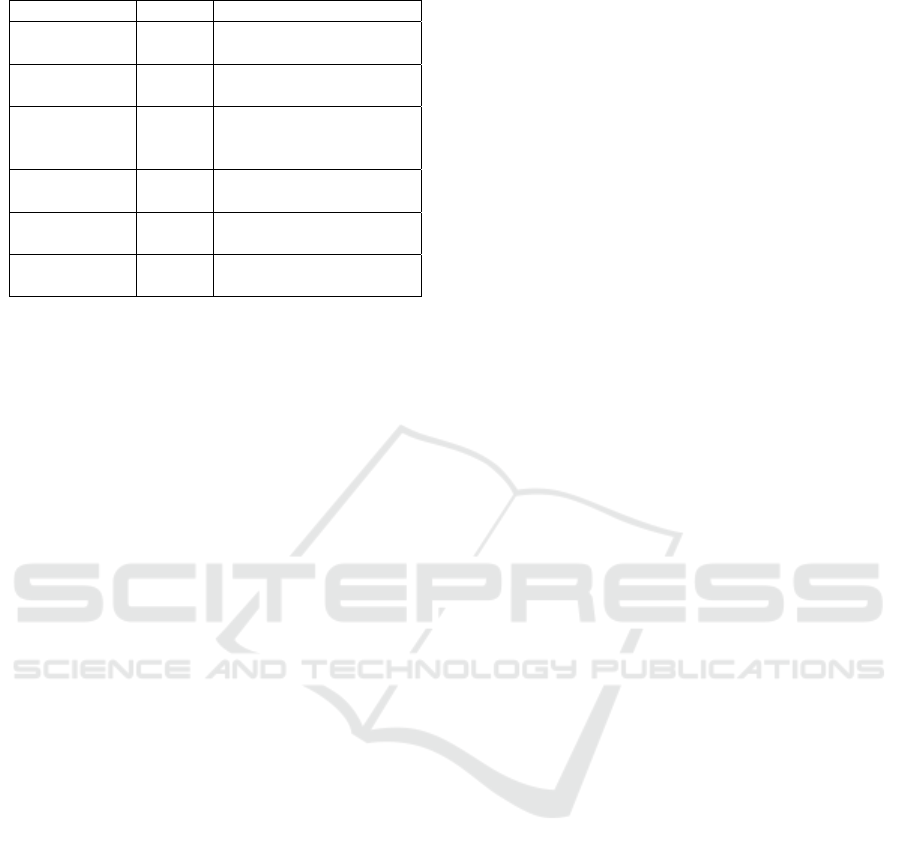
Table 7: Overall profile and descriptions.

Metric Value Descri

tion

Annualized

Return

8.32% Annualized return of the

optimized

ortfolio

Sharpe Ratio -1.399 Risk-adjusted return based

on the

ortfolio volatilit

Calmar Ratio 0.231 Return-to-risk ratio

considering maximum

drawdown.

Annualized

Volatilit

8.46% Standard deviation of the

ortfolio’s returns.

Maximum

Drawdown

36.32% Maximum observed loss

from a

eak to a trou

CVaR (95%) -1.464 Expected loss in extreme

market conditions

3.6 Limitations and Prospects

The limitations of this study are mainly in several

aspects. First, Due to under dynamic market

conditions, traditional static models may not

adequately reflect actual market volatility (Campbell

& Viceira, 2002). The study operates under the

assumption that market conditions remain relatively

stable and does not thoroughly account for the effects

of dynamic factors like market sentiment and

macroeconomic changes on investment portfolios.

Second, the historical data used may not fully reflect

future market volatility and risk, and thus the results

of the study may be subject to a certain degree of

uncertainty in practical application. Moreover, the

analysis is concentrated on a narrow set of asset

categories, excluding other investment instruments

like bonds and real estate, which could reduce the

overall diversification and risk management of the

portfolio. Future research could further enhance

portfolio performance by introducing real-time data

analytics and machine learning models to adjust

portfolios more dynamically in response to market

changes and uncertainties.

4 CONCLUSIONS

To sum up, the goal of this study is to construct an

optimized portfolio that maximizes risk-adjusted

returns. By applying modern portfolio theory,

including mean-variance optimization, Capital Asset

Pricing Model (CAPM), Conditional Value-at-Risk

(CVaR), and Maximum Drawdown Analysis, one

determines the optimal asset allocation: 50% for

Apple, 10% for Crude Oil, 30% for SPY, and 10% for

Bitcoin. The portfolio has an expected annualized

return of 8.32% and annualized volatility of 8.46%,

effectively balancing risk and return. The use of the

CAPM model in asset pricing is widely supported.

While this study provides a solid framework for

portfolio optimization, it is limited by assuming static

market conditions and excluding dynamic factors

such as market sentiment. Modern portfolio theory

plays an important role in asset allocation. Future

research could explore the integration of real-time

data and machine learning models to further improve

portfolio performance. Although there are certain

limitations, the research sheds light on the critical role

of strategic asset distribution and effective risk

management in securing consistent, long-term returns.

REFERENCES

Baur, D. G., Hong, K., Lee, A. D., 2018. Bitcoin: Medium

of Exchange or Speculative Assets. Journal of

International Financial Markets, Institutions and

Money, 54, 177-189.

Campbell, J. Y., Viceira, L. M., 2002. Strategic Asset

Allocation: Portfolio Choice for Long-Term Investors.

Oxford University Press.

Cheung, Y. W., Miu, P., 2010. Diversification Benefits of

Commodity Futures. Journal of International Money

and Finance, 29(3), 396-408.

Elton, E. J., Gruber, M. J., Brown, S. J., Goetzmann, W. N.,

2007. Modern Portfolio Theory and Investment

Analysis. John Wiley Sons.

Fama, E. F., French, K. R., 2004. The Capital Asset Pricing

Model: Theory and Evidence. Journal of Economic

Perspectives, 18(3), 25-46.

Goetzmann, W. N., Li, L., Rouwenhorst, K. G., 2005.

Long-Term Global Market Correlations. Journal of

Business, 78(1), 1-38.

Jagannathan, R., McGrattan, E. R., 1995. The CAPM

Debate. Quarterly Review, 19(4), 2-17.

Jorion, P., 2006. Value at Risk: The New Benchmark for

Managing Financial Risk. McGraw-Hill.

Markowitz, H. M., 1991. Portfolio Selection: Efficient

Diversification of Investments. Blackwell Publishers.

Rockafellar, R. T., Uryasev, S., 2000. Optimization of

Conditional Value-at-Risk. Journal of Risk, 2(3), 21-42.

APPENDIX

Appendix 1: Original Data: https://docs.google.com/spread

sheets/d/1W1QmlLgwWWc5PAI4q1RFyHpN2H8M5

f7l/edit?usp=sharing&ouid=102167542405241696605

&rtpof=true&sd=true

Appendix 2: Data cleaning: https://docs.google.com/spread

sheets/d/1-RRsvqImCkYFhWrln5OIt3lEj0ubl2cT/

edit?usp=sharing&ouid=102167542405241696605&rt

pof=true&sd=true

Appendix 3: Tresure data: https://ycharts.com/indicators

/10_year_treasury_rate

Portfolio Design and Optimization Based on the CAPM Model

475