Fraud Detection in Smart Contracts Anomaly Detection

Zeyuan Lyu

School of Computer and Network Security (Model Software School), Chengdu University of Technology, Chengdu, China

Keywords: Fraud Detection, Blockchain, Machine Learning.

Abstract: Fraud detection is nowadays a critical issue in the blockchain domain, particularly due to the increasing

volume of transactions and the associated risks of fraudulent activities. This study focuses on detecting

fraudulent transactions within the Ethereum network by employing three different machine learning

classifiers: logistic regression, random forest, and XGBoost, respectively. This paper trained and tested these

models on a dataset composed of various transaction features to assess their performance. After implementing

empirical examining, the results revealed that the tree-based models, specifically the random forest and

XGBoost classifiers, significantly outperformed logistic regression in detecting fraudulent activities. The

superior performance of these models highlights their robustness in handling high-dimensional data, which is

often characteristic of blockchain transactions. This study not only confirms the effectiveness of tree-based

models in fraud detection but also offers valuable insights for future research in the field, paving the way for

more secure and reliable blockchain trading systems.

1 INTRODUCTION

One crucial challenge facing the financial industry is

the detection of fraud, particularly within the rapidly

evolving blockchain technology. As digital

transactions become more widespread, the potential

for fraudulent activities increases, making it essential

to develop robust methods for identifying and

mitigating such risks. Ethereum, as one of the leading

blockchain platforms, is widely used for various

transactions, but its open and decentralized nature

also makes it susceptible to fraudulent activities.

Identifying fraudulent transactions on the Ethereum

blockchain is vital for maintaining the integrity of the

network and ensuring trust among users.

Various applications of fraud detection have been

explored in different domains. For example, Aydos

(2020) focused on detecting and analyzing crypto

ransomware, a growing threat in the cybersecurity

space, where attackers demand ransom in

cryptocurrency after encrypting victims' files. In

another application, blockchain technology has been

employed in healthcare insurance fraud detection to

securely manage and monitor insurance activities,

addressing the issue of false claims and ensuring the

integrity of insurance data (Saldamli et al., 2020).

https://orcid.org/0009-0007-5094-7322

Beyond specific applications, researchers have

investigated machine learning techniques to enhance

fraud detection. Bhowmik et al. (2021) provided a

comparative study of supervised machine learning

algorithms like decision trees, Naive Bayes, and

logistic regression for identifying fraudulent

transactions on blockchain platforms. Additionally,

Shayegan et al. (2022) proposed a collective anomaly

detection method to identify fraudulent behaviors

among Bitcoin users, outperforming previous

methods in detecting anomalies across multiple

wallets. Furthermore, Jung et al. (2019) used a data

mining approach to discover Ponzi scams on

Ethereum, improving precision and recall in

identifying such fraudulent activities. Moving

towards more complex models, neural network

applications have been investigated by several

researchers, though these models typically suffer

from lower real-time performance and

interpretability. For instance, Singh et al. (2021)

introduced a Graph Neural Network (GNN) with

temporal debiasing to enhance the generalization of

fraud detection models over time, though this

approach still faces challenges in real-time

application and clarity of interpretation. Similarly,

Tan et al. (2021, 2023) applied a Graph

462

Lyu, Z.

Fraud Detection in Smart Contracts Anomaly Detection.

DOI: 10.5220/0013268800004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 462-468

ISBN: 978-989-758-726-9

Convolutional Network (GCN) to detect fraudulent

transactions in Ethereum, achieving high accuracy

but encountering similar issues with real-time

efficiency and interpretability. Finally, Hu et al.

(2023) proposed a more advanced approach involving

a transformer model that has been trained beforehand,

BERT4ETH, for the purpose of detecting Ethereum

fraud. This model demonstrated superior

performance in capturing dynamic transaction

patterns, but it too faces limitations in real-time

performance and interpretability, which are common

drawbacks in neural network-based models.

This study conducts a comprehensive evaluation

of three machine learning models—logistic

regression, random forest, and XGBoost—applied to

Ethereum transaction data. The first step involved

data preprocessing, where irrelevant and redundant

features were removed to enhance model efficiency.

After that, the transformed dataset was used to train

and test each model, and their performances were

compared based on various metrics, including

accuracy, precision, recall, and F1-score. Both the

random forest and XGBoost models demonstrated

strong performance, with each offering specific

advantages depending on the scenario.

The findings of this study provide valuable

insights into the application of machine learning for

blockchain fraud detection, highlighting the strong

balance these models achieve between

interpretability, classification accuracy, and

computational speed. Moreover, they offer a solid

foundation for further studies aimed at improving the

precision and effectiveness of fraud detection systems

in the blockchain ecosystem.

2 DATA SET

2.1

Source and Description

This dataset is from the kaggle website. The dataset

has 9841 rows (number of samples) and 50 columns

(number of features). The first few rows of this

dataset, the first row is the index, the Address column

is the address of the Ether, and the FLAG column

denotes a binary label. The other columns denote

features of various trading behaviors, such as the

number of contracts created. The data range of the

dataset, transaction behavior features are including

the time interval between sending and receiving

transactions, the number of transactions sent and

received, the number of contracts created, etc. ERC20

related features, including the minimum, maximum,

and average ERC20 tokens transaction values, etc.

There is statistical information in the data such as

maximum, minimum, and average values of some

features, for example, the maximum value of Sent tnx

(number of transactions sent) is 49542, and the

minimum value is 0.

2.2

Data Preprocessing

First, LabelEncoder is imported as a tool to convert

the categorical data into numerical labels, then all the

object columns are label coded, and the counts of

each label value in the FLAG column are printed out,

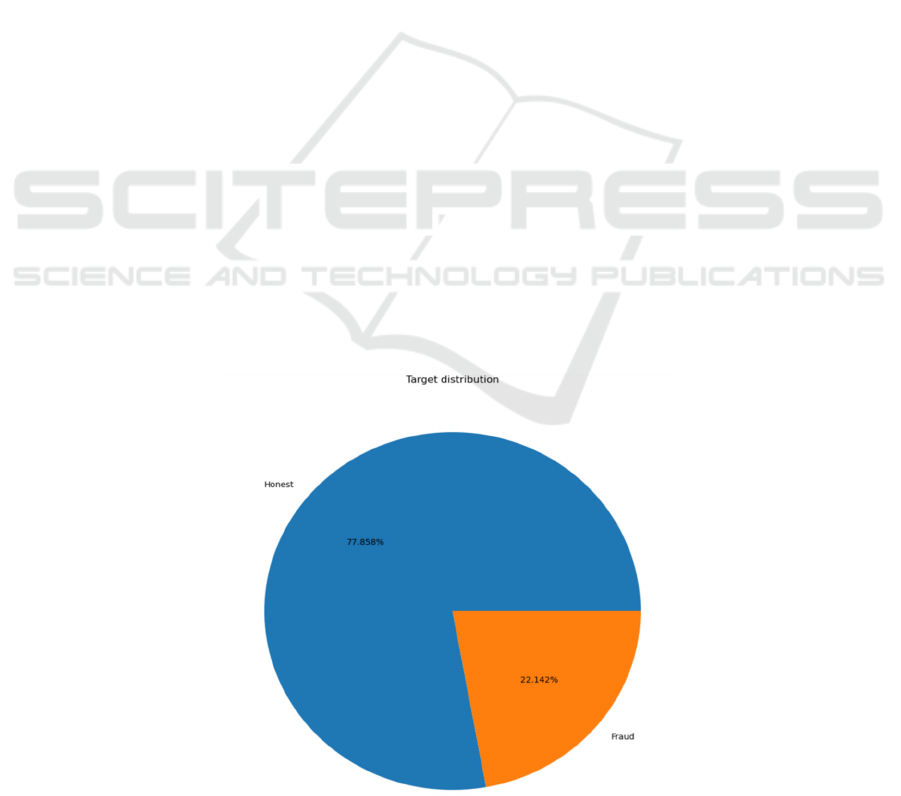
and finally the pie figure is plotted with the names of

labels for the two categories, which are "Honest" and

"Fraud". The relevant results are presented in Figure

1 below.

Figure 1: Distribution of honesty and fraud.

Fraud Detection in Smart Contracts Anomaly Detection

463

As can be seen from this figure, about 77. 9% of

the records are labeled as "honest" while about 22.1%

are labeled as "fraudulent" This figure clearly shows

the distribution of the two categories in the data set.

To refine the dataset and enhance the predictive

value of the remaining features, a comprehensive

correlation analysis was conducted. The initial step

involved identifying and removing columns with zero

variance, also known as constant values. These

columns do not contribute any useful information to

the model since their values do not change across the

dataset.

Following this, features with high correlation

were carefully examined. In a dataset, when two

features are highly correlated, they provide redundant

information. To avoid this redundancy and reduce the

dimensionality of the dataset, one feature from each

pair of highly correlated features was removed.

Specifically, if the correlation has an absolute value

between two features exceeded 0.4, one of them was

excluded from the dataset. This process ensured that

only the most relevant and non-redundant features

were retained, thereby improving the efficiency and

accuracy of the model.

This meticulous elimination of constant and

highly correlated features allowed for a clearer and

more precise analysis, enabling a better

understanding of the relationships between the

remaining features and their potential predictive

power.

3 METHODOLOGIES

3.1 Logistic Regression

The argument for the appropriateness of the model is

made first. In fraudulent transaction detection, the

most important thing to care about is the probability

of the transaction occurring. When the probability of

the model output exceeds a certain threshold, it can

be excluded from fraud. Logistic regression is a linear

model widely evaluated for binary classification

tasks. It predicts the category of the target variable by

mapping a linear combination of input features into a

probability space. The core idea is to convert the

output of the linear regression model into a

probability value between 0 and 1 through the

decision function. This probability value reflects the

model's confidence in the category to which a certain

sample belongs.

Logistic regression provides a high degree of

interpretability compared to more complex models

such as neural networks or ensemble methods. The

coefficients of the model directly reflect the

contribution of each feature to the final decision, this

means that it is possible to clearly see which

characteristics are more likely to result in a

transaction being considered fraudulent. This is

especially useful for fraud detection on the ETH

chain, because transactions and addresses are often

complex and diverse, and by interpreting the model

coefficients, it can help us better understand the

characteristic patterns of fraudulent behavior.

The data used in this paper is close to 10,000

pieces, and each piece of data has multiple features.

Logistic regression has low computational

complexity and is suitable for processing large-scale

data sets. It is a linear model, and its training and

prediction processes are efficient. The basic formulas

and principles of the model are as follows.

Linear model:

𝑧 = 𝛽



+ 𝛽



𝑥



+ 𝛽



𝑥



+ ⋯+ 𝛽



𝑥



(1)

The Sigmoid function:

𝑝(𝑦 =1∣𝐱)=𝜎(𝑧)=

𝑒



(2)

First assume that there is a linear relationship

between the input feature x and the output result as

follows. Where β0 is the intercept term, (β1, β2....βn)

is the coefficient of the feature (x1, x2....xn)

corresponding to the coefficients. The Sigmoid

function is then used to convert z to a probability as

follows. This probability represents the probability

that the target value y is 1 given the feature x.

However, in the code of this model, the model is

trained by the fit method, that is, optimizing the

parameters in the above equation to minimize the

prediction error.

3.2 Random Forest Classifier

Random forest is an ensemble learning method that

mainly improves the accuracy and stability of

forecasts through the construction of several decision

trees, voting on them, and averaging their outcomes.

The core idea is that by combining the prediction

results of multiple models, the bias and variance that

a single model may bring can be reduced.

This method constructs different decision trees by

randomly selecting feature subsets and sample

subsets to ensure that each tree has a certain degree of

diversity. Since these trees are constructed

independently of each other, errors in a single tree do

not significantly affect the performance of the overall

model. Random forest models are adept at capturing

complex, nonlinear relationships within the data. This

capability stems from the ensemble approach, where

multiple decision trees, each with its own view of the

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

464

Figure 2: Random Forest.

data, collectively contribute to the final

prediction. This diversity among the trees allows the

model to handle intricate patterns and interactions

that a single decision tree might miss. As a result,

random forests often deliver highly accurate

predictions.

Additionally, random forests are known for their

efficiency in training compared to many other

machine learning techniques. This is because the

construction of individual trees is inherently

parallelizable: each tree can be built independently of

the others. Consequently, this parallelism can

significantly speed up the training process. The basic

formulas and principles of the model are as follows.

Majority voting (classification issues).

𝑦 =mode



𝑦



, 𝑦



,,𝑦





(3)

where 𝑦 is the final prediction and 𝑦



is the

prediction of the ith tree. Here is the visualization of

the model (See Figure 2).

A random forest is an integrated model consisting

of multiple decision trees, the structure of one of

which is shown in Fig. This tree has multiple layers

of nodes, demonstrating the complexity of the model,

which can handle high-dimensional feature data and

make complex classification decisions, and is able to

fit the details of the training data very well, with a

very low error on the training data. However, this

overfitting may lead to poor performance on test data

and risk of overfitting.

In the last part of the code, a concrete decision tree

is visualized with the plot_tree function. The tree

shows the splitting process over different features and

provides the final classification decision for each leaf

node. feature_names parameter specifies the names of

the features, and the filled=True parameter makes the

node color correlate with the classification result,

with the darker color representing the model's

confidence in that classification. For decision tree

visualization methods can help us understand how a

single tree inside a random forest makes decisions,

and by analyzing the structure of these trees, the

model can be further optimized, and its parameters

can be adjusted to improve performance.

3.3

XGB Classifier

XGBoost uses the gradient boosting method, which

means it builds decision trees sequentially. Each new

tree is constructed to correct the errors made by the

previous trees, leading to gradual improvements in

the model's performance.

Meanwhile, the construction of each tree depends

on the results of the previous tree, allowing the model

to make fine adjustments and increase prediction

accuracy.

XGBoost and Random Forest models are both

based on tree structures. Random Forest tends to build

trees simultaneously, while XGBoost sequentially

improves tree parameters step by step. These different

approaches help to more comprehensively

demonstrate the effectiveness of tree-based

classification algorithms. Here are the basic equations

for the model.

Additive Model:

𝑦



()

= 𝑦



()

+ 𝜂

𝑓



(

𝑥



)

(4)

Gradient Descent:

𝑔



()

∂𝐿𝑦



, 𝑦



()



∂𝑦



()

(5)

Fraud Detection in Smart Contracts Anomaly Detection

465

AUC(Area under the ROC curve):

AUC = 





TPR (𝑡) ⋅FPR (𝑡)𝑑𝑡

(6)

In the formula TPR is the true positive rate and

FPR is the false positive rate.

XGBoost builds the model in an additive manner,

where the prediction at step t is given by the additive

model formula. 𝜂 is the learning rate, 𝑓



(

𝑥



)

is the

new tree added at step t. 𝑦



()

is updated prediction. To

minimize the loss function, XGBoost uses the

gradient of the loss function with respect to the

predictions. The update for each tree is based on the

negative gradient as 𝑔



()

In the code, the coordinates of the ROC curve are

calculated by the roc_curve function and the AUC

value is calculated by the auc function, this can assist

us understand the model's categorization

performance. The last part of the code uses the

plot_confusion_matrix function to plot the confusion

matrix, which is used to show the classification effect

of the model to visualize the comparison between the

real categories and the predicted categories. In

addition, the false positive rate is represented by the

horizontal axis of the ROC curve, the vertical axis

reflects the actual positive rate, the closer the ROC

curve is to the upper left corner, the stronger the

classification ability of the model, and the larger the

AUC value is, the better the overall performance of

the model.

4 RESULTS

4.1 Logistic regression

The confusion matrix regarding logistic regression is

shown below in Table 1.

Table 1: Results of the confusion matrix.

Categories

Actual-

on-

Frau

Actual-Frau

Predic

on-Frau

1538 4

Predic

-Frau

11 416

The model correctly predicted 1538 class 0

samples, and only 4 class 0 samples were incorrectly

categorized as class 1, indicating that the model

performs very well for class 0 sample prediction. The

model correctly predicted 416 class 1 samples, and

only 11 class 1 samples were misclassified as class 0,

which is also a very good performance. It can be seen

that the model's classification accuracy is very high.

The model predicts the accuracy rate as follows in

Table 6.

Table 6: The prediction accuracy of the model

recision recall F1-

score

suppor

0 0.99 1.00 1.00 1542

1 0.99 0.97 0.98 427

accurac

0.99 1969

Macro avg 0.99 0.99 0.99 1969

Wei

ht av

0.99 0.99 0.99 1969

It is known from the data that the model has a very

high overall precision, recall, F1 score, and individual

prediction precision for both class 0 and class 1,

which indicates that the model performs very well

overall and has a very low misclassification rate.

ROC for tuned XGB Classifier as follows in Figure 3.

A positive and negative sample are picked at

random, and the probability that the classifier

correctly determines that the value of the positive

sample is greater than that of the negative sample is

the AUC. So, a classifier with a larger AUC value has

a higher rate of correctness. As shown in the figure,

the ROC curve is close to the upper left corner (almost

right angle), which indicates that the model performs

Figure 3: ROC curve.

Fraud Detection in Smart Contracts Anomaly Detection

467

well in distinguishing in the range of positive and

negative samples. The AUC value of 0.999, which

tends to 1, indicates that the model has excellent

classification performance. As the rate of false

positive cases increases, the rate of true cases also

increases significantly, indicating that the model can

effectively recognize positive samples.

4.4 Model Comparisons

Comparing the total prediction precision of the

model, predictive accuracy of class 0 and class 1

respectively, the recall rate, and the F1 score, the

following conclusions can be drawn that the XGB

Classifier model has a higher degree of classification

accuracy and a relatively low misclassification rate,

which makes it more suitable for handling this task.

5 CONCLUSIONS

Fraud detection on blockchain platforms like

Ethereum is of paramount importance due to the

increasing prevalence of digital transactions. This

study evaluated the effectiveness of logistic

regression, random forest, and XGBoost classifiers in

identifying fraudulent activities within Ethereum

transaction data. Through rigorous model training and

testing, it was found that both the random forest and

XGBoost models provided robust performance, with

each model demonstrating unique strengths. These

findings underscore the value of tree-based models in

managing high-dimensional data and contribute to the

ongoing efforts to enhance fraud detection

mechanisms within the blockchain ecosystem.

Future study may investigate the incorporation of

more powerful machine learning algorithms, such as

deep learning, to further increase the accuracy and

efficiency of fraud detection. Additionally,

investigating the applicability of these models in real-

time fraud detection systems and their scalability

across different blockchain platforms could provide

valuable insights for practical implementation.

REFERENCES

Bhowmik, M., Chandana, T. S. S., & Rudra, B. (2021,

April). Comparative study of machine learning

algorithms for fraud detection in blockchain. In 2021

5th international conference on computing

methodologies and communication (ICCMC) (pp. 539-

541). IEEE.

Hu, S., Zhang, Z., Luo, B., Lu, S., He, B., & Liu, L. (2023,

April). Bert4eth: A pre-trained transformer for

ethereum fraud detection. In Proceedings of the ACM

Web Conference 2023 (pp. 2189-2197).

Jung, E., Le Tilly, M., Gehani, A., & Ge, Y. (2019, July).

Data mining-based ethereum fraud detection. In 2019

IEEE international conference on blockchain

(Blockchain) (pp. 266-273). IEEE.

K. A. R. A., & Aydos, M. (2020, October). Cyber fraud:

Detection and analysis of the crypto-ransomware. In

2020 11th IEEE Annual Ubiquitous Computing,

Electronics & Mobile Communication Conference

(UEMCON) (pp. 0764-0769). IEEE.

Nayyer, N., Javaid, N., Akbar, M., Aldegheishem, A.,

Alrajeh, N., & Jamil, M. (2023). A new framework for

fraud detection in bitcoin transactions through

ensemble stacking model in smart cities. IEEE Access.

Singh, A., Gupta, A., Wadhwa, H., Asthana, S., & Arora,

A. (2021, December). Temporal debiasing using

adversarial loss based GNN architecture for crypto

fraud detection. In 2021 20th IEEE International

Conference on Machine Learning and Applications

(ICMLA) (pp. 391-396). IEEE.

Saldamli, G., Reddy, V., Bojja, K. S., Gururaja, M. K.,

Doddaveerappa, Y., & Tawalbeh, L. (2020, April).

Health care insurance fraud detection using blockchain.

In 2020 seventh international conference on software

defined systems (SDS) (pp. 145-152). IEEE.

Shayegan, M. J., Sabor, H. R., Uddin, M., & Chen, C. L.

(2022). A collective anomaly detection technique to

detect crypto wallet frauds on bitcoin network.

Symmetry, 14(2), 328.

Tan, R., Tan, Q., Zhang, P., & Li, Z. (2021, December).

Graph neural network for ethereum fraud detection. In

2021 IEEE international conference on big knowledge

(ICBK) (pp. 78-85). IEEE.

Tan, R., Tan, Q., Zhang, Q., Zhang, P., Xie, Y., & Li, Z.

(2023). Ethereum fraud behavior detection based on

graph neural networks. Computing, 105(10), 2143-

2170.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

468