Research on Deep Learning in Stock Price Prediction

Xinyi Xiong

College of Software and IoT Engineering, Jiangxi University of Finance and Economics,

No. 665 Yuping West Street, Nanchang, China

Keywords: Deep Learning, Stock Price Prediction, Neural Network, Time Series.

Abstract:

Stock trading is an important way for people to invest and make profits. The process of gathering and

evaluating historical stock data and information, condensing the rules governing the growth of the stock

market, and applying scientific research techniques to forecast the future direction of the stock market's price

trend is known as "stock price prediction". Basic mathematical models serve as the foundation for traditional

stock price research. Originally, stock data was processed by financial experts using basic linear models.

However, due to the large amount of noise and uncertainty factors in stock data, the limitations of linear

models become increasingly prominent as the prediction period lengthens. Researchers have made an effort

to employ nonlinear models in their work, effectively implementing techniques like support vector machines

and neural networks in stock prediction. With an emphasis on the use of both deep learning-based and

conventional statistical model-based approaches for stock price prediction, this article reviews the evolution

and modifications in research methodologies for this purpose. It also summarizes and prospects the future

development of deep learning in stock price prediction.

1 INTRODUCTION

With the country's economy growing quickly and

living standards rising steadily, investing has become

a popular way for individuals to preserve and increase

the value of their personal assets. The stock market

has developed from its initial stage to the present and

has become an indispensable part of the market

economy. Stock investment, with its potential high

returns and corresponding high risks, has become one

of the most widely accepted investment channels for

ordinary people, and it is also a manifestation of

optimizing the allocation of social resources.

An increasing number of investors are drawn to

the stock market since it is a vital component of the

financial system. As a direct reflection of market

sentiment and investment trends, stock prices

naturally become the focus of investors' attention. By

examining past trading data, investors hope to

uncover the underlying trends and features of stock

prices. Nevertheless, the nonlinearity and high

volatility of stock price fluctuations, which are caused

by a number of factors, make investing in stocks

blindly risky. Therefore, establishing an accurate

stock price prediction model has significant practical

significance for investors.

Traditional statistical models predict stock prices

by establishing mapping relationships between inputs

and outputs. They typically assume that stock data is

linear and stable, making them suitable for situations

with small data scales. However, in today's stock

market, stock data often has the characteristics of

large-scale, nonlinear, and high noise, and using these

traditional models for prediction often fails to achieve

the expected accuracy.

As big data and artificial intelligence technologies

advance, modern stock price prediction models are

increasingly adopting machine learning and deep

learning techniques, which can process larger scale

data, capture more complex nonlinear relationships,

and improve prediction accuracy. However, Since the

stock market is so complex and unpredictable, no

model can provide a prediction accuracy of 100%, so

investors still need to be cautious when applying

these models and make investment decisions based on

market conditions and their own experience.

Hum Nath Bhandari, Binod Rimal, Nawa Raj

Pokhrel, Ramchandra Rimal, Keshab R. Dahal and

Rajendra K.C. Khatri build single-layer and multi-

layer Long Short-term Memory Neural Networks

(LSTM) models and use 11 selected predictor

variables to predict the next day closing price of the

S&P 500 index. Research has found that single-layer

156

Xiong, X.

Research on Deep Learning in Stock Price Prediction.

DOI: 10.5220/0013244300004558

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Modern Logistics and Supply Chain Management (MLSCM 2024), pages 156-162

ISBN: 978-989-758-738-2

LSTM models have significantly better prediction

accuracy than multi-layer models, with the single-

layer model consisting of 150 neurons performing the

best. According to the experimental findings, the

single-layer model performs better in evaluation

indicators than the multi-layer model, such as RMSE,

MAPE, and correlation coefficient R, verifying its

effectiveness and superiority in stock market

prediction (Bhandari, Rimal, Pokhrel, Rimal, Dahal

and Khatri, 2022). In order to anticipate the closing

price of stock prices on the following trading day, Lu

Wenjie, Li Jiazheng, Wang Jingyang, and Wu

Shaowen developed a composite model called CNN

Attention GRU Attention that combines

Convolutional Neural Networks (CNN), Attention,

and Gated Recurrent Units (GRU) (Lu, Li, Wang and

Wu, 2022). The model has improved its predictive

performance through feature selection and structural

improvements. The basic model used to calculate

stock prices is GRU; features are extracted from stock

price data using CNN; the impact of various time

states on forecasted values is calculated using

Attention. The results indicate that CNN Attention

GRU Attention has the maximum accuracy when

compared to six other models. When it comes to stock

price prediction, the composite model structure

outperforms single or basic composite models in

terms of accuracy. It is

crucial for investors and regulatory bodies to

comprehend the stock market, and the CNN Attention

GRU Attention model offers several potential

applications. Savinderjit Kaur and Veenu Mangat

proposed a DE-SVM hybrid model for selecting the

optimal free parameter combination of Support

Vector Machine (SVM) to improve prediction results.

And it is concluded that the performance of SVM is

significantly affected by its free parameter selection

(Kaur and Mangat, 2012). The performance of the

DE-SVM model is comparable to that of PSO-SVM,

and normalization of the dataset can significantly

enhance the model's functionality. By assigning equal

weights to each input variable and converting all

variable values into a predefined range, normalization

increases the model's efficiency. SVM performs

better in data normalization because optimization

techniques in mixed models help adjust the model

according to the requirements of the dataset. In

addition, they also proposed that in the future,

Dynamic Differential Evolution (DDE) and

Differential EvolutionParticle Swarm Optimization

(DEPSO) can be used to optimize SVM, in an effort

to boost SVM's effectiveness and prediction results'

accuracy even more.

This article will introduce the application of deep

learning in stock price prediction from four models:

time series models, neural network models, SVM and

hybrid models. Time series models include

Autoregressive Moving Average Model (ARMA)

and Auto Regressive Integrated Moving Average

(ARIMA) models, neural network models include

CNN, Recurrent Neural Network (RNN), and LSTM

models, and combination models include RNN-CNN

and LSTM-CNN models. This article will introduce

the principles of the above models and summarize the

advantages and disadvantages of each model. Finally,

based on the current situation of domestic and

international stock price prediction models, directions

for improvement are pointed out.

2 RESEARCH METHODS AND

APPLICATIONS

2.1 Time Series Model

2.1.1 Autoregressive Moving Average Model

Taking autocorrelation and moving average into

account, ARMA combines the features of

Autoregressive (AR) and Moving Average (MA)

models. The ARMA model is a comprehensive

framework whose features increase the accuracy of

the information interpreted and the

comprehensiveness of the information it contains.

Moreover, this model has good performance in

handling both stationary and non-stationary time

series. The ARMA model is a commonly used model

in time series analysis, used to describe and predict

the dependency relationships between data points.

The ARMA model is a combination of AR model and

MA model. The AR model focuses on the relationship

between current values and past values in a time

series, while the MA model focuses on the

relationship between current values and past error

terms in a time series (Rounagh and Zadehb, 2016).

It can be used with stationary time series data, which

is time series data whose statistical characteristics,

including variance and mean, do not change over time.

2.1.2 Auto Regressive Integrated Moving

Average Model

ARIMA adds differential operations to the ARMA

model for processing non-stationary time series data.

The further development of the ARMA model is the

ARIMA model, which adds a differential (I) part for

processing non-stationary time series data. Through

differential operation, non-stationary time series are

Research on Deep Learning in Stock Price Prediction

157

transformed into stationary time series using the

ARIMA model, and then applies the ARMA model

for modeling (Kobielaa, Kreftaa, Krol and

Weichbroth, 2024). The ARMA model is suitable for

short-term forecasting and is relatively accurate in

predicting the daily opening price of stocks. However,

the inaccuracy in long-term projections might be

large since several factors affect stock values.

Therefore, ARMA models are more suitable for

short-term forecasting.

2.2 Neural Network Model

Neural networks, structured by their design, are

classified into three primary types: Artificial Neural

Networks (ANN), CNN, and RNN. ANN comprises

both feedforward models, often known as BP

networks, and a range of recurrent models, which

include the basic RNN, LSTM networks, and GRU

networks.

2.2.1 Convolutional Neural Network Model

CNN is a feedforward neural network proposed by

Lecun et al. in 1998 that includes convolution

operations. It exhibits the capability to analyze

extensive temporal datasets and pictorial information,

thereby finding broad application in the domain of

feature construction. CNN has five layers of network

structure, namely input layer, convolutional layer,

pooling layer, fully connected layer, and output layer.

The convolutional and pooling strata constitute

multi-tiered configurations within deep learning

architectures, and they alternate between each other.

Compared with traditional machine learning model

algorithms, CNN mainly face more complex

nonlinear relationships in data through three steps:

local connections, parameter sharing, and

downsampling. CNN mines deeper data features by

increasing the number of network layers and

processes them into more representative data features

through its unique convolutional pooling structure

(Hoseinzade and Harati, 2019). However, when

employing the feature extraction functionality of

CNN to derive comprehensive and multifaceted

attributes of equities, the selection of convolutional

kernels should not be too large, otherwise there may

be a decrease in accuracy.

2.2.2 Recurrent Neural Network Model

RNN was first proposed by Hopfeld in 1983 and is

often used to handle more complex time series data.

Traditional neural networks do not have memory

function because they assume that each layer's

network nodes are independent of each other, without

any connections in between, and each input

information is an independent individual. The reason

why RNN is called recurrent neural network is

because it changes this idea by processing the input

information from the previous moment and storing it

in a hidden layer, forming a short-term memory. This

implies that the current output is not solely contingent

upon the present input, but is also significantly

influenced by the preceding output (Saud and Shakya,

2020). This makes it perform well on complex time

series tasks. This cycle repeats itself, forming a fully

connected structure from front to back between

layers. In the conventional neural network

architecture, an additional hidden layer is interposed

between the input and output layers. As the amount

of input data and the number of iterations increase,

the processing ability of RNN for long time series

becomes weaker, leading to phenomena such as

gradient explosion and gradient disappearance.

Specifically, data that is temporally distant from the

present moment is considered, the model may

experience forgetting.

Due to the fact that RNN models only have the

ability to learn from data that is relatively recent, they

cannot effectively handle long time series. Although

this problem can theoretically be solved by adjusting

the parameters of the hidden layer, it cannot be

significantly enhanced and requires a great deal of

time and work to adapt. Thus, the improved structure

LSTM of RNN emerged.

2.2.3 Long Short-Term Memory Network

Model

LSTM is an improved model of RNN neural network,

proposed by Hochreiter and Schmidhuber in 1997.

The proposal of LSTM is fundamentally aimed at

solving the problems of gradient vanishing and

exploding in RNN when memorizing data, and the

inability to accurately process long time series

through parameter adjustment. As an improved model

of RNN, the basic idea behind the LSTM neural

network is to address the limitations of RNN by

leveraging the human brain's mechanisms for

selective memory and selective forgetting. The input

gate, forget gate, and output gate are the three

interconnected storage nodes that make up the LSTM

network's replacement of the RNN hidden layer

network topology. This system of gating units

regulates the information flow. Which data in the

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management

158

memory unit should be kept and which should be

erased is decided by the forget gate.

The input gate controls when important

information is inputted first. Output gates are used to

control which memory unit states can be output to the

next neuron.

However, LSTM models have high complexity,

slow computation speed, and low fitting performance.

And its sensitivity to extreme values is low, making

it impossible to maintain extremely high prediction

accuracy.

2.3 Support Vector Machine Model

SVM maps data to a high-dimensional space through

kernel functions and finds the optimal separation

hyperplane in that space (

Chhajer, Shah and Kshirsagar,

2022)

. In stock price prediction, SVM can be used for

classification (such as predicting stock price

fluctuations) or regression (predicting specific price

values), learning patterns and patterns from historical

data through training. Studies have been conducted to

forecast trends and variations in stock prices using

ensemble learning techniques and SVM. For instance,

modeling and forecasting changes in stock prices

while accounting for the influence of several market

variables and technical indicators can be done using

random forests.

SVM training, however, can be somewhat

complicated, particularly if the dataset is big or

contains a lot of characteristics. This may result in

long training time and high demand for computing

resources. Also, the choice of parameters has a

significant impact on SVM accuracy, such as kernel

function type, penalty parameter C, and kernel

parameters. Choosing appropriate parameters often

requires methods such as cross validation, which may

increase the complexity and time cost of model

construction. The decision-making process of SVM

models is often difficult to explain, especially when

using nonlinear kernel functions. In addition, SVM is

sensitive to outliers and noise, which is a challenge in

financial markets as historical data may contain

outliers and market volatility noise.

2.4 Hybrid Model

2.4.1 Recurrent Neural Network

Convolutional Neural Network Model

RNN-CNN model combines the advantages of RNN

and CNN, using RNN to process time series data,

capture the temporal dependence of stock prices, and

using CNN to identify local characteristics in time

series data. The RNN-CNN model considers

technical indicators of stocks, which are calculated

based on historical trading data and reflect

information such as market volatility and trends. The

RNN-CNN model preprocesses data, including

normalizing the data, combining basic and technical

indicators of stocks, and performing dimensionality

reduction to reduce the complexity of model training

(Guan, 2023).

The RNN-CNN model includes the following four

layers of applications:

Model input: The input of the model includes the

basic indicators of the stock and the calculated

technical indicators, which are preprocessed and

utilized by the model as training data.

RNN layer: The model uses RNN layers to extract

temporal features of time series data, and can adopt

different variants of RNN, such as LSTM or GRU.

CNN layer: To improve the model's capacity to

identify local patterns, the CNN layer further extracts

spatial characteristics based on the information that

the RNN layer has extracted.

Fully connected layer: The collected features are

combined using the fully connected layer, which

comes after the RNN and CNN layers, to get the

ultimate forecast output.

2.4.2 Long Short Term Memory

Convolutional Neural Network Model

Combining characteristics of LSTM and CNN for

predicting stock prices. In order to increase prediction

accuracy through feature fusion, this model makes

use of several representations of time series data and

image data. Time series data features, such historical

stock price data, are extracted using the LSTM

network. Learning long-term reliance in data

sequence is a particularly good use case for LSTM,

since it may retain relevant information while

discarding irrelevant information. Features, including

stock price charts, are taken out from picture data by

CNN networks.

CNN performs well in image recognition and feature

extraction, capturing local features and constructing

more complex and abstract feature representations

layer by layer.

This model consists of the following four layers:

Input layer: Receive basic and technical indicators

of stocks, which can include the opening price,

highest price, lowest price, closing price, trading

volume, etc;

Feature extraction layer: The LSTM layer

processes time series data and extracts temporal

Research on Deep Learning in Stock Price Prediction

159

features; CNN layer processes stock chart images and

extracts spatial features;

Feature fusion layer: combines the features that

were retrieved using CNN and LSTM to create a

complete characteristic presentation;

Fully connected layer: further processes and maps

the fused features, and finally outputs the predicted

stock price.

Studies have demonstrated when it comes to

market price prediction, the LSTM-CNN system

performs better than models that only use LSTM or

CNN. Especially, the LSTM-CNN model that

integrates Candlestick Chart features performs the

best, proving that combining time and image features

can effectively reduce prediction errors (Liu, 2023).

3 EXPERIMENTAL DATA

3.1 Factors Affecting Stock Prices

Basic data of stock trading: In order to cover a wide

range of areas, such as the basic data of 8 stocks

including opening price, maximum price, minimum

price, closing price, rise and fall points, range, trading

volume and turnover.

Stock technical indicators: MA and MACD are

moving average indicators, and price following

indicators can accurately reflect recent price changes;

CCI and WR are indicators of overbought and

oversold types; ATR is a quantitative indicator that

represents the current long short state and possible

trends in stock price development and changes; ADX

is a trend indicator; OBV trading volume indicator.

The macro basic environment of the stock market

includes political factors, economic factors, exchange

rates, and interest rates. However, most models only

use the first two indicators as input data for the model.

3.2 Dataset Selection

The stock trading information of the forestry, farming,

livestock breeding, and fishing industries as well as

the historical trading information of three stocks

under these industries were arranged using Tushare

open data.

Acquired the "SSE 50 Index" component

weighting information from TuShare, and selected

the top 30 stocks with higher weights to form the

stock input dataset. Representative individual stock

data include Kweichow Moutai, China Merchants

Bank, Ping An, Industrial Bank, Shanghai Pudong

Development Bank, etc.

3.3 Experimental Result

Evaluation indicators: Root Mean Square Error

(RMSE), Mean Absolute Error (MAE), and

Coefficient of Determination (R ² _Score) are

employed to assess the model's capacity for

forecasting.

The regression indicator MAE can accurately

represent the true error, RMSE reflects the degree of

dispersion of a dataset, R ² represents the extent to

which the model's predicted values explain the

changes in input values, or can show how well the

projected values fit the data. The more accurate the

projected values and the greater the model's forecast

accuracy, the smaller the values of the MAE and

RMSE error indicators. The more near the number of

R ² is to 1, the stronger the impact of forecasting and

the level of fit between the true and forecast values.

This is the model's matching ability or predictive

capacity indicator.

Table 1 displays the outcomes of the experiment.

It is evident from the information shown in the table

that the LSTM model works greater in terms of

prediction than the RNN model. The CNN Attention

GRU Attention model outperforms the GRU model in

forecasting, but the LSTM-CNN model outperforms

a single LSTM model in this regard. Consequently,

compared to a single simple system, the hybrid

system structure typically has a higher accuracy in

stock price prediction.

4 CHALLENGES AND

PROSPECTS

4.1 Challenges

The generalization capabilities of a deep learning

model: While these models might work well with

training data, they might not work as well with

unknown data or market conditions.

High demand for data resources: The training of

deep learning models sometimes necessitates a

substantial amount of computational power, which

may restrict their use in situations with limited

resources.

Data Quality: For training, deep learning models

usually need a lot of high-quality data. There could be

noise in the stock market data.

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management

160

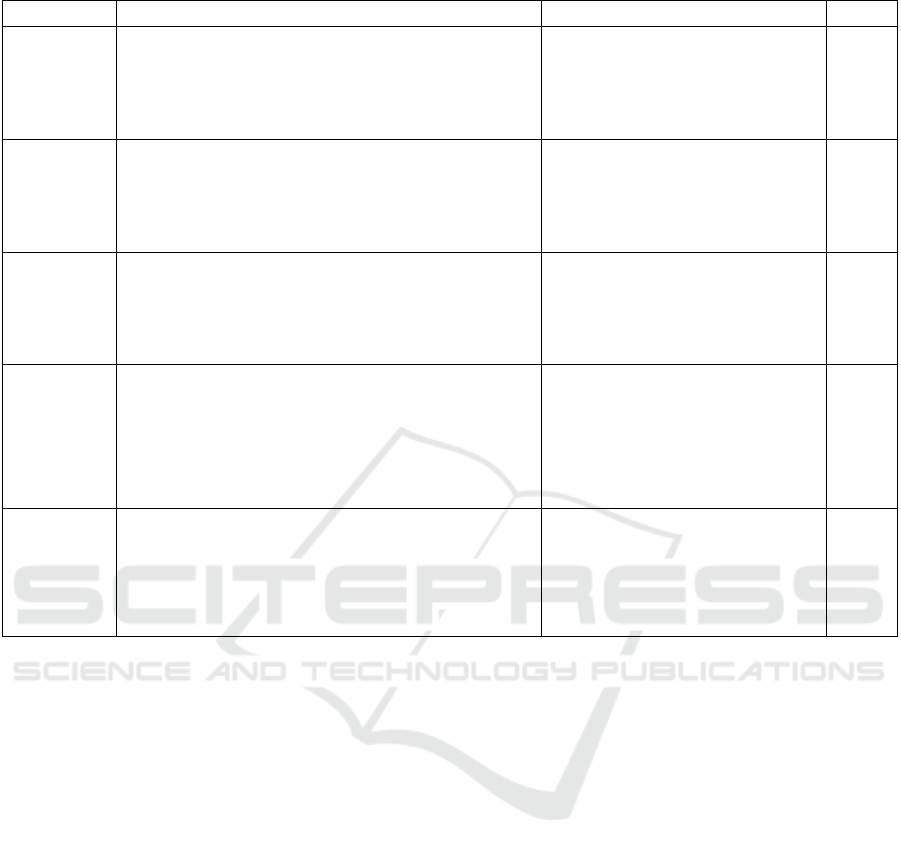
Table 1: Comparison table of characteristics, effects, and R² of five models.

Model name characteristic effect

R²

RNN

It is a neural network suitable for sequence prediction

problems, which can capture dynamic features in time

series

RNN can provide relatively accurate

stock price predictions, especially in

short-term market volatility

forecasting

0.8145

LSTM

Capable of learning long-term dependency

relationships and effectively solving the problem of

gradient in RNNs disappearing or exploding when

processing sequential data

LSTM can usually provide high

prediction accuracy, especially when

dealing with stock price data with

significant time dependence

0.8583

GRU

It is an RNN version that adds update gates and reset

gates to address the issue of gradient disappearing or

exploding in conventional RNNs when processing long

sequence data

The GRU model shows good

prediction accuracy in capturing

short-term fluctuations and long-term

trends of stock prices

0.9642

LSTM-

CNN

It can handle time-series information of prices for

stocks, capturing both short- and long-term trends as

well as periodic fluctuations by combining the benefits

of CNN and LSTM. Additionally, local characteristics

in stock price statistics, like the form and pattern of

price swings, can be obtained through this method

Can more accurately predict

changes in stock prices, and can

effectively generalize to fresh data

following training, lowering

possibility of overfitting

0.9297

CNN-

Attention-

GRU-

Attention

It is a deep learning model that combines CNN,

attention mechanisms, and GRU, particularly suitable

for processing complex data with time series

characteristics

By comprehensively utilizing

multiple mechanisms, it is possible

to more accurately capture the

complex changes in stock prices,

thereby improving prediction

accuracy

0.9671

4.2 Future Prospects

Model optimization: To increase the prediction

accuracy and generalization capacity for deep

learning models, future study can further enhance

their structure and methods.

Multi model fusion: Combining multiple

prediction models, such as combining deep learning

with other machine learning methods, to increase

forecast stability and precision.

Data augmentation: To increase the size of the

training sample and increase the model's flexibility in

response to shifting market conditions, apply data

enhancement approaches.

Real-time prediction: To keep up with the stock

market's swift movements, create models that can

process data in immediate time and generate

predictions fast.

Cross market application: Apply deep learning

models to stock markets in different countries and

regions, considering the characteristics and

differences of different markets.

Risk management: Combining deep learning

models with risk management strategies to provide

investors with more comprehensive risk assessment

and investment advice.

5 CONCLUSIONS

The deep learning methods utilized in forecast of

stock prices are introduced in this article. These

methods include the commonly employed CNN,

RNN, and LSTM neural networks. These models can

extract time series information from stock price data

as well as intricate nonlinear properties. The majority

of the forecasting of stock prices models are based on

historical trading data, including opening price,

highest price, lowest price, closing price, trading

volume, etc. Deep learning models predict future

prices by learning patterns from this data. Nowadays,

many researchers try to combine time series model

and neural network model to form hybrid model, such

as CNN-RNN model, CNN-LSTM model and

Research on Deep Learning in Stock Price Prediction

161

ARIMA-RNN model. In general, a hybrid model's

prediction power outperforms that of just one model.

This has led more and more businesses and

enterprises to adopt hybrid models for short-term

forecasting of stock market information, in order to

obtain greater returns.

In future research, researchers can further

optimize and improve traditional prediction models,

or combine multiple models to implement hybrid

models to raise the precision of forecasts and keep

growing the training dataset to make the model more

flexible in response to shifting market circumstances.

REFERENCES

Bhandari, H. N., Rimal, B., Pokhrel, N. R., Rimal, R., Dahal,

K. R., Khatri, R. K. C., 2022. Predicting Stock Market

Index Using LSTM. In Machine Learning with

Applications, Volume 9, 15 September 2022, 100320.

Lu, W. J., Li, J. Z., Wang, J. Y., Wu, S. W., 2022. A Novel

Model for Stock Closing Price Prediction Using CNN-

ATTENTION-GRU-ATTENTION. In Economic

Computation and Economic Cybernetics Studies and

Research, Issue 3/2022; Vol. 56.

Kaur, S., Mangat, M., 2012. Improved Accuracy of PSO

and DE Using Normalization: an Application to Stock

Price Prediction.In International Journal of Advanced

Computer Science and Applications, Vol. 3, No. 9.

Rounagh, M. M., Zadehb, F. N., 2016. Investigation of

Market Efficiency and Financial Stability Between

S&P 500 and London Stock Exchange: Monthly and

Yearly Forecasting of Time Series Stock Returns Using

ARMA Model. In Physica A: Statistical Mechanics and

its Applications, Volume 456, 15 August, Pages 10-21.

Kobielaa, D., Kreftaa, D., Krol, W., Weichbroth, P., 2024.

ARIMA vs LSTM on NASDAQ Stock Exchange

Data.In Procedia Computer Science, Volume 207, 2022,

Pages 3836-3845.

Hoseinzade, E., Harati, S., 2019. CNNpred: CNN-based

Stock Market Prediction Using a Diverse Set of

Variables.In Expert Systems with Applications,

Volume 129, 1 September 2019, Pages 273-285.

Saud, A. S., Shakya, S., 2020. Analysis of Look Back

Period for Stock Price Prediction with RNN Wariants:

A Case Study on Banking Sector of NEPSE.In Procedia

Computer Science, Volume 167, 2020, Pages 788-798.

Chhajer, P., Shah, M., Kshirsagar, A., 2022. The

Applications of Artificial Neural Networks, Support

Vector Machines, and Long–short Term Memory for

Stock Market Prediction. In Decision Analytics Journal

2 (2022) 100015.

Guan, J., 2023. Research on Stock Price Prediction Method

Based on RNN-CNN Model. In Nanjing university of

information science and technology Master's degree

thesis.

Liu, Z., 2023. Research on Stock Price Prediction Modeling

Based on CNN-LSTM and Transfer Learning. In

Harbin Normal University, CLC Number: O15.

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management

162