Exploring the Influence of Country, Industry, and Gender Features

in Machine Learning-Based Rich List Prediction

Juming Zhang

Faculty of Engineering, The University of Queensland, Brisbane, Queensland, 4072, Australia

Keywords: Machine Learning, Rich List Prediction, Linear Regression.

Abstract: In the context of economic globalization, the global rich list is also undergoing subtle changes year by year.

From a macro perspective, the impact of countries, industries, and gender on personal assets cannot be ignored.

This study will use learning models to predict the 2025 rich list, and use information visualization to draw

images and machine learning to explore the impact of different features on the list, so as to understand the

global wealth distribution, analyze market and industry trends, and infer whether gender has an impact on the

rich industry. The study found that when using a linear model for prediction, the best prediction effect is to

build a separate model for each rich person. At present, the concentration of wealth in the United States is

relatively high, far exceeding other countries among the rich, but China, Russia, India, Germany, the United

Kingdom and other countries also have certain advantages on the rich list, showing their importance in their

respective fields. Technology, finance and fashion have a significant impact on the wealth accumulation of

the rich. Gender currently has little impact, reflecting gender equality among the rich.

1 INTRODUCTION

Most people will be very curious when they hear

about the rich list, and the media and public attention

to these lists also makes them a hot topic. Some

people will seek opportunities to learn from the rich

list, study the investment strategies, business models

and management experience of these rich people, and

apply them to their own business or investment. The

rich people on the list often represent the top level of

certain industries, and their experience may be of

reference value to many people who hope to succeed

in related fields (Davies, 2017). Therefore, the study

of the rich list is also very meaningful.

The significance of studying the rich list (such as

the Forbes Billionaire List) is broad and far-reaching,

involving multiple levels such as economy, society,

politics, and culture (Neumayer, 2004). Firstly,

through the rich list, it could be clearly understood the

distribution of global wealth and identify which

countries or regions have more wealth accumulation.

Studying the rankings helps analyze the extent to

which wealth is concentrated in a few people, as well

as the changing trends in the gap between the rich and

the poor, thereby providing a basis for the formulation

of economic policies (Krcmaric, 2024).

Secondly, analyzing the industry background of

the rich can help identify which industries are on the

rise. For example, in recent years, a large number of

new rich people have emerged in the technology

industry, reflecting the rapid growth of the

technology industry. The growth in the number of

wealthy people and their wealth is an important

indicator of economic vitality and national economic

strength, and can reflect the health of the economy.

Thirdly, studying the rich list can help investors

identify market hot spots and potential investment

opportunities. For example, by analyzing the wealth

growth of the rich in a certain industry, investors can

adjust their investment strategies. For entrepreneurs,

knowing which industries have created the wealthiest

people can guide them in choosing promising

entrepreneurial directions.

This study mainly used machine learning and

information visualization methods (Mahesh, 2020).

The machine learning models include linear

regression models and decision tree models, and the

information visualization method is to draw charts

related to different features. In the past, researchers

mainly used macroeconomic analysis and stock

market valuation to predict. However, this study used

modern machine learning algorithms can process

large amounts of data and make full use of many years

Zhang, J.

Exploring the Inﬂuence of Country, Industry, and Gender Features in Machine Learning-Based Rich List Prediction.

DOI: 10.5220/0013231500004558

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Modern Logistics and Supply Chain Management (MLSCM 2024), pages 66-72

ISBN: 978-989-758-738-2

of historical data for training, thereby improving the

accuracy of predictions. In addition, machine learning

models, especially complex models like random

forests, decision trees, and neural networks, are able

to capture nonlinear relationships and complex

patterns in data, which gives them an advantage over

traditional statistical methods in predicting trends and

changes in the growth of wealth among the rich

(Dhall, 2020). And machine learning can also be used

to extract important information from a large number

of features, such as country, industry, age, etc., to help

identify key factors that affect wealth growth. This

study used machine learning to explore the

relationship between the rich list and country,

industry, and gender, and then inferred the

relationship between personal wealth and the three.

The advantage of visualization is that it can present

complex data results in a simple and intuitive form,

so that non-technical personnel can understand it.

This study uses pie charts, bar charts, trend lines and

other charts to clearly reveal the distribution and

changes of wealth.

2 METHOD

2.1 Data Acquisition and Processing

The dataset used in this study is the annual rich list

from 1997 to 2024. The data for each year is a two-

dimensional table, where the attributes include

ranking, name, net worth, country, industry, age,

gender, position, whether it is self-made, and ranking

change. For the initial data processing, since the data

from 1997 to 2014 is relatively old, and the data from

1997 to 2006 is incomplete, and the rankings are

updated very quickly, the impact of 1997 to 2014 on

the prediction is relatively low, so it is ignored.

Finally, the data set from 2015 to 2024 is used for

prediction. The attributes used are: ranking, name, net

worth, country, industry, gender, year (Guillem,

2024).

2.2 Machine Learning Models

This study used three machine learning models: linear

regression model, polynomial regression model, and

random forest model. The linear regression model

prediction is to build a model for each rich person,

and regress and fit the net assets of each rich person

in previous years (Su, 2012). Finally, the year is

substituted into the model to predict the net assets of

each rich person in 2025, and finally the prediction

results are obtained by sorting. Polynomial regression

prediction is divided into two methods in this

experiment (Heiberger, 2009). The first is to build a

polynomial model for the entire data set, and the

second is to build a polynomial model for each rich

person. Both methods use ranking, country, industry,

gender, and year as features, and assets as output

results, and then sort them for prediction. At the same

time, polynomial regression also tries to use only

assets as features to make polynomial fitting

predictions in the second method. The purpose is to

compare with the prediction results of adding more

factors, use linear regression models to analyze the

factors that predict the changes in the net worth of the

rich, and use coefficients to judge the degree of

influence of different features on the changes in net

assets. The random forest model first measures the

importance of the features of country, industry,

gender, ranking, and year, and then combines the

characteristic factors of each feature to predict each

rich person (Rigatti, 2017).

2.3 Evaluation Indicators

This study mainly used two evaluation indicators:

Mean Square Error (MSE) and Coefficient of

Determination (R²) (Ozer, 1985).

MSE calculates the prediction error of the model.

MSE is the average of the sum of squares of the errors

between the predicted value and the true value. The

smaller the MSE, the lower the prediction error of the

model.

R² measures the explanatory power of the model.

R² represents the correlation between the predicted

value and the true value, and the value range is [0, 1].

The closer R² is to 1, the stronger the explanatory

power of the model.

The model testing method is K-fold cross-

validation: K-fold cross validation is a commonly

used model evaluation technique to evaluate the

performance and generalization ability of machine

learning models. It achieves more reliable model

evaluation by dividing the dataset into multiple

subsets.

This validation method is to first divide the dataset

into K subsets (folds). Each subset is called a fold. In

each iteration, one of the folds is used as the

validation set, and the remaining K-1 folds are used

as training sets. In K iterations, a different fold is used

as the validation set each time to evaluate the model

performance. The average of the K evaluation results

is calculated as the final performance indicator of the

model. In this test, the dataset is divided into 5 or 10

folds to increase the reliability of the validation

results. The advantage of K-fold cross validation is

Exploring the Inﬂuence of Country, Industry, and Gender Features in Machine Learning-Based Rich List Prediction

that by training and validating the model on different

data subsets, the overfitting of the model to the

training set can be reduced. Each data point is used as

a training and validation set once, which helps to

more accurately evaluate the generalization ability of

the model.

3 STATISTICAL ANALYSIS

In this work known data sets are leveraged to draw

pie charts, line charts, and bar charts for

demonstrating the top 200 richest people each year

based on country, industry, and gender.

3.1 Analysis of Country Distribution

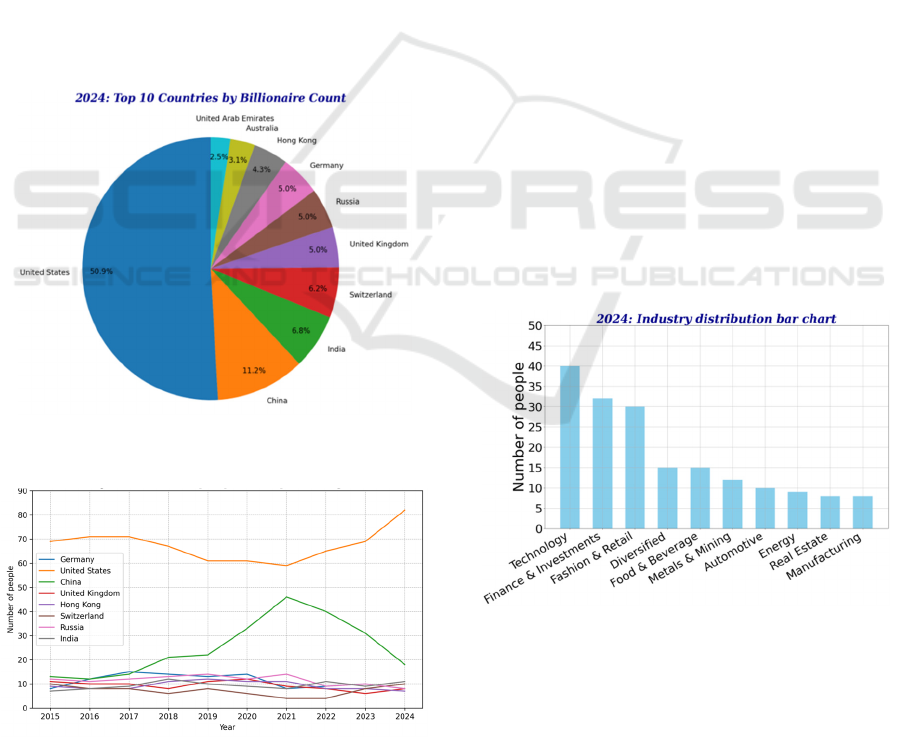
Figure 1 shows the distribution of the top 10 countries

in 2024. Figure 2 shows the line chart of the changes

in the number of people on the list of the top ten

countries in each year from 2015 to 2024.

Figure 1: Distribution of top 10 countries in the rich list in

year 2024 (Figure Credits: Original).

Figure 2: Tendency of rich list changes over years in top

ranking countries (Figure Credits: Original).

From Figure 2, it can be seen that the United

States (US) accounts for 45% of the richest people,

indicating that the US occupies an important position

in the global rich list. This may be closely related to

factors such as the US economic scale, innovation

ability, maturity of the financial market, and

entrepreneurial spirit. In addition, As the world's

second largest economy, China has seen an increase

in the number of its wealthy people year after year,

reflecting the country's rapid economic growth and

wealth accumulation. China's business environment

and market opportunities have promoted the growth

of local wealthy people. What is more, Countries such

as Germany, the United Kingdom, Russia, India,

Hong Kong, and Switzerland also maintain a certain

presence in the global rich list, showing their

importance in their respective economic sectors. For

example, Germany's industry and manufacturing, the

United Kingdom's financial services, Russia's energy

industry, India's technology and entrepreneurship,

Hong Kong's financial markets, and Switzerland's

financial confidentiality and high net worth

population management all contribute to their

position in the global rich list.

3.2 Analysis of Industry Distribution

Figure 3 shows a bar chart of the number of people in

the top 200 of the rich list by industry in 2024. Figure

4 shows a line chart of the number of people in the

top ten industries in the past five years.

Figure 3: Distribution of top 10 industries in the rich list in

year 2024 (Figure Credits: Original).

From Figure 4, it can be seen that the technology

industry occupies a prominent position in the rich list,

and in the past ten years, the technology industry has

accounted for the highest proportion almost every

year. This shows that the technology industry has a

huge impact on the wealth accumulation of the rich.

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management

Moreover, in 2024, Finance & Investment also

frequently appeared in the top three of the rich list,

which shows that the finance and investment industry

plays an important role in the accumulation of wealth.

Besides, emerging industries (such as food and

beverage, manufacturing, etc.) gradually entered the

rich list. This shows that although technology, finance

and fashion retail are the main sources of wealth,

other industries are also beginning to play an

increasingly important role.

Figure 4: Tendency of rich list changes over years in top

ranking industries (Figure Credits: Original).

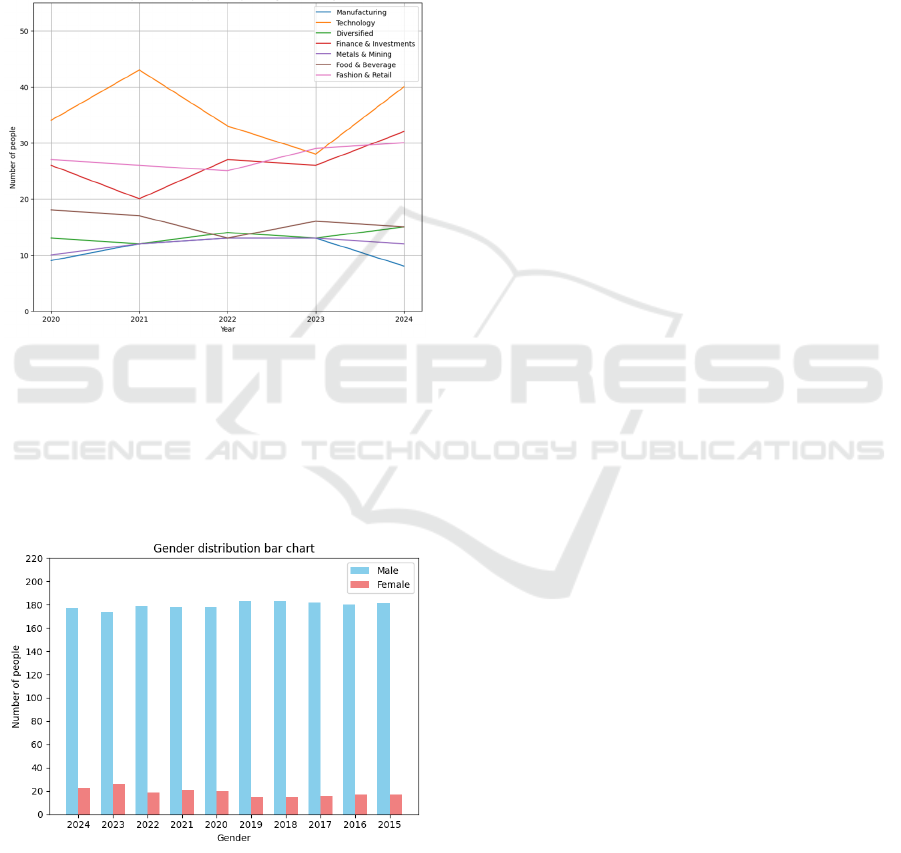
3.2 Analysis of Gender Distribution

Figure 5 shows the number of men and women in the

top 200 richest people list each year from 2015 to

2024.

Figure 5: Distribution of gender in the rich list from year

2015 to 2024 (Figure Credits: Original).

From Figure 5, it can be seen that the male to

female ratio is about 9:1 every year, which may mean

men’s advantages in wealth accumulation and

economic opportunities may indicate gender

inequality. In many industries and regions, women

may face more barriers or restrictions.

4 EXPERIMENTS AND RESULTS

4.1 Experimental Setups

4.1.1 Setting of Linear Regression

The core of linear regression is to use the least squares

method to fit at the first order. Specifically, the role

of the least squares method is to find a linear model

that minimizes the sum of squared errors between the

model's predicted values and the actual values. This

is a common regression analysis method used to fit a

linear relationship on a given data set.

Before data input, standardization is used to

process the data, making the entire training process

more stable and effective. Standardization adjusts the

mean of the features to 0 and the standard deviation

to 1, so that all features are trained on the same scale.

This helps prevent certain features from having too

much influence on the model, which can lead to an

unstable learning process.

In the experiments, the data years earlier than the

current forecast year is used for training and the data

of the current forecast year for testing.

4.1.2 Setting of Polynomial Regression

This article uses three methods to perform polynomial

prediction: (1) Use only year as feature and assets as

target variable. (2) Make a pipeline model for each

rich person, where the features of each model are: net

assets, country, industry, gender, and the assets of

each rich person are the target variable of each model

(3) Use pipeline model for overall data, with features

of country, industry, gender, year, and assets as target

variable. All three methods predict the net assets of

each rich person in 2025 and then rank them.

Polynomial Method 1: First, group the data by

the names of the rich and make predictions for each

rich person individually. That is, build a polynomial

regression for each rich person. Then select year as

feature and wealth as target variable. And the year

characteristics are standardized (The data is still

transformed into a standard normal distribution with

a mean of 0 and a variance of 1).

When building a model, Pipeline is used to create

a polynomial regression model, including feature

transformation and linear regression. Polynomial

Features is then used to generate polynomial features,

Exploring the Inﬂuence of Country, Industry, and Gender Features in Machine Learning-Based Rich List Prediction

specifying different degrees (that is, orders) to

capture nonlinear relationships and compare

prediction results of different orders.

Here is some explanation of the pipeline model.

The Pipeline Model is a method used in machine

learning to string together multiple data processing

and modelling steps. The Pipeline model can

integrate multiple steps such as data preprocessing,

feature selection, feature conversion, and model

training into a unified workflow, greatly improving

the maintainability and reusability of the code and

reducing manual operations and human errors.

Train the model using historical data of each rich

person. Finally, substitute the year into the trained

model for prediction. Polynomial regression can

capture more complex trends by using higher-order

features. It can fit nonlinear relationships compared

to simple linear regression.

Polynomial Method 2: Similar to method one,

but a pipeline model is built for each rich person and

features such as country, industry, and gender are

added through one-hot encoding for polynomial

fitting prediction. Use ColumnTransformer (a method

from the sklearn. compose package in Python) to

standardize features (for years) and one-hot encode

(for categorical variables). Create a Pipeline that

includes polynomial features and a linear regression

model. Train the model using the data for each rich

person.

For non-numerical information such as country,

industry, and gender, this experiment uses one-hot

encoding to convert them into binary vectors. In this

vector, only one position is 1, and the rest are 0. This

position corresponds to the position of the category

among all possible categories. The features converted

by One-Hot Encoding are passed to the model as

input data. The model learns the relationship between

the features and the target variable based on the

values of these features, thereby automatically

determining the weight of each feature. Through

training, the model adjusts the weight of each feature

to minimize the prediction error.

Finally, 2025 is entered into the established model.

Make predictions and keep the rich people whose

prediction results are greater than zero. (The rich

people predicted with negative values are at the

bottom of the rankings over the years, and the net

assets of the rankings are in billions, while their assets

on the rankings are close to 1, so the model has a

greater impact on them)

Polynomial Method 3: Finally, the third method

uses a pipeline model, with country, industry, gender,

year, and assets as target variables. It standardizes the

Year column to eliminate the dimension effect of

numerical features, similar to the previous methods.

Then this method creates a multinomial regression

model through the pipeline.

4.1.3 Setting of Random Forest

The core idea of random forest model is to improve

the stability and accuracy of the model by combining

the prediction results of multiple decision trees. A

decision tree is constructed for each subset, and the

training data for each tree is different. When splitting

at each node, a portion of the features are randomly

selected for consideration instead of using all the

features. This makes the trees different and reduces

overfitting.

This study uses random forest to measure the

importance of different features, which is equivalent

to the weight of the impact on the prediction results,

and then substitutes the established model into the

2024 data for prediction.

In this model, the following features are selected

for analysis: Rank, Country, Business Category,

Gender, and Year. Wealth (Billion $) is used as the

target variable for prediction. This method converts

categorical variables into numerical features so that

they can be input into the model for training. Here,

pandas.get_dummies is used to convert categorical

variables (such as country, industry, and gender) into

one-hot encoding form.

In this experiment dataset is split into a training

set and a test set with a ratio of 70% and 30%. This is

a common practice in machine learning to ensure the

performance of the model on unseen data. And set the

maximum depth to 10 to prevent overfitting

4.2 Model Comparison

Through linear regression analysis, it can visualize

the importance of different features in predicting the

difference in the net assets of the rich, and provide the

importance ranking of each feature. Feature

importance and coefficients can provide explanations

and analysis of the prediction model, helping people

understand which factors have the greatest impact on

the prediction results.

Table 1: Result comparison of different models.

Model MSE R

linear re

ression 8.3 0.64

nomial model method1 171.5 0.7

olynomial model method2 320.7 0.17

olynomial model method3 17.1 0.97

random tree 65.6 0.28

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management

Table 1 shows the MSE and R

calculated for each

model and method. Table 2 shows the most accurate

prediction among all the model calculation results,

showing the top 20 prediction rankings

Table 2: Predicted wealth of rich list.

Rank Name

Wealth

(Billion $)

1 Bernard Arnault & famil

236.1

2 Elon Mus

226.6

3 Jeff Bezos 202.6

4 Warren Buffett 165.2

5 Bill Gates 133

6 Larr

Ellison 130.8

7 Mark Zuckerber

124.7

8 Larr

e 116.7

9 Steve Ballme

113.8

10 Sergey Brin 112.5

11 Michael Bloomberg 104.6

Francoise Bettencourt

Meyers & family

104.1

13 Rob Walton & famil

97.2

14 Qin Yinglin & famil

93.9

15 Mukesh Ambani 93.3

16 Carlos Slim Helu & famil

91.5

17 Gautam Adani 87.1

18 Amancio Ortega 83.2

19 Alice Walton 81.2

20 Jim Walton 81.1

These results of linear regression model shows

that the prediction model is more reliable at the top of

the prediction list, and the prediction becomes less

reliable as it goes further back, because the top rich

have a large wealth base, while the opposite is true for

the rich at the bottom of the ranking.

In Polynomial method1, the data results show that

pure numerical prediction is not accurate. It is

possible to add more features for increasing the

accuracy of prediction.

In Polynomial method 2, the results show that the

prediction results of this model are poor. Compared

with method 1 and method 3, it can be seen that

building a model for each rich person is more accurate

than using the overall data model to make predictions.

In Polynomial method 3, the results show that the

model fits well. It shows that the best prediction

results are obtained by building a model for each

billionaire separately and adding characteristics such

as country, industry, gender, etc.

4.2 Feature Importance Analysis

The result of random forest shows that the decision

tree prediction considers the country and business to

have a higher degree of influence, as shown in Table

3. However, due to the low accuracy of the

calculation, it is possible to add other features that

have a greater impact on the rankings.

Table 3: Feature importance measured from random forest

results.

Feature Feature Importance

Countr

Business 0.63

Yea

0.37

Gende

A further investigation shows the top 20 features

and their coefficients among all the correlation

coefficients of the linear regression model. It could be

found that investment, finance, food and beverage

and other industries play an important role in the

predicted asset differences. The influence of East

Asian countries cannot be underestimated.

5 CONCLUSIONS

This article used information visualization to draw

pictures to intuitively find the characteristic factors

that may affect the rich list, and then use machine

learning to predict different results under different

characteristic conditions. The linear regression model

is mainly used to compare the results of linear fitting

predictions based on the assets of each rich person

with the results of linear fitting based on assets and

other factors (country, industry, gender). In this way,

it could be found out the impact of country, industry

and gender on the rich list. And this work uses the

random forest model to analyze the weight ratio of

different characteristics.

Finally, this study found that when a linear

regression model was established for each rich

person, the accuracy after verification was the

highest. It was also found that the year and ranking

had a greater impact on the results.

It may reflect the impact of time trends on the

wealth of billionaires. This can be understood as the

overall economic environment, technological

progress, global market dynamics and other factors

will affect the accumulation of billionaire wealth over

time. The ranking is not only a number, it also reflects

the fierce competition among billionaires around the

world. The rich who can stay at the top may have

competitive advantages in certain aspects (such as

business vision, market share, etc.). From a national

level, other countries also have significant wealthy

individuals, but their proportion is relatively small

compared to the United States, reflecting the uneven

Exploring the Inﬂuence of Country, Industry, and Gender Features in Machine Learning-Based Rich List Prediction

distribution of global wealth. From an industry

perspective, the technology industry has the greatest

impact on wealth accumulation, mainly due to its

innovation and market drivers. The financial and

investment industries play an important role in wealth

management and capital operations. The fashion and

retail industries have a stabilizing impact on wealth

accumulation, reflecting the value of brands and

consumer markets. The growth of emerging

industries indicates an increase in the diversity of

wealth accumulation, which may lead to changes in

wealth distribution. The results show that gender has

little effect, probably because the number of male

billionaires in the dataset is far greater than that of

female billionaires, and the model may automatically

ignore the importance of gender because its impact on

the prediction results is negligible.

REFERENCES

Davies, J. B., Lluberas, R., & Shorrocks, A. F. 2017.

Estimating the level and distribution of global wealth,

2000–2014. Review of Income and Wealth, 63(4), 731-

759.

Dhall, D., Kaur, R., & Juneja, M. 2020. Machine learning:

a review of the algorithms and its applications. Procee

dings of ICRIC 2019: Recent innovations in computing,

47-63.

Guillem, SD. 2024. Forbes Billionaires Evolution 1997-20

24. Kaggle Dataset, URL: https://www.kaggle.com/da

tasets/guillemservera/forbes-billionaires-1997-2023. L

ast Accessed: 2024/08/08

Heiberger, R. M., Neuwirth, E., Heiberger, R. M., &

Neuwirth, E. 2009. Polynomial regression. R Through

Excel: A Spreadsheet Interface for Statistics, Data

Analysis, and Graphics, 269-284.

Krcmaric, D., Nelson, S. C., & Roberts, A. 2024. Billionai

re Politicians: A global perspective. Perspectives on P

olitics, 22(2), 357-371.

Mahesh, B. 2020. Machine learning algorithms-a

review. International Journal of Science and

Research, 9(1), 381-386.

Neumayer, E. 2004. The super-rich in global perspective: a

quantitative analysis of the Forbes list of

billionaires. Applied Economics Letters, 11(13), 793-

796.

Ozer, D. J. 1985. Correlation and the coefficient of

determination. Psychological bulletin, 97(2), 307.

Rigatti, S. J. 2017. Random forest. Journal of Insurance

Medicine, 47(1), 31-39.

Su, X., Yan, X., & Tsai, C. L. 2012. Linear regression. Wil

ey Interdisciplinary Reviews: Computational Statistic

s, 4(3), 275-294.

MLSCM 2024 - International Conference on Modern Logistics and Supply Chain Management