Portfolio Construction Based on LSTM RNN and Black-Litterman

Model: Evidence from Yahoo Finance

Junzhe Wang

Department of Bigdata, Beijing Institute of Technology, Beijing, China

Keywords: LSTM RNN, Black-Litterman Model, Omega Matrix, View, Bias.

Abstract: Portfolio optimization is always a tough issue in fiance field. This study explores the integration of Long

Short-Term Memory (LSTM) Recurrent Neural Networks (RNN) with the Black-Litterman model (BL

model) to improve portfolio optimization. The BL model, which combines the views from the investors with

market equilibrium to modify the revenues that are expected, is commonly used for asset allocation. Yet the

model has a few limitations, including subjectivity, data sensitivity, and complexity. In order to deal with

these issues, the paper proposes incorporating LSTM RNN predictions into the BL model to mitigate bias and

enhance decision-making. The study utilizes historical data from Yahoo Finance for four major

corporations(Apple;Intel;Google;NVIDIA) from January 2023 to August 2024. The LSTM RNN is trained

on this data to generate machine predictions, which are then treated as investor views in the BL model. The

Omega matrix, representing the uncertainty or confidence in these predictions, is adjusted to combine machine

and investor perspectives. Results indicate that while LSTM RNN predictions can improve price forecasting,

they also introduce biases that require careful calibration. The modified BL model, incorporating machine-

generated views, provides a more personalized and potentially more accurate portfolio allocation. This

approach offers a novel way to balance human and machine insights in financial decision-making, though it

requires significant computational resources and expertise to implement effectively. Future research might

focus on refining the Omega matrix estimation and exploring alternative machine learning models to further

enhance the model's robustness.

1 INTRODUCTION

The concept of portfolio was first proposed by Medici

family in the 15th century during the renaissance in

Italy. It was used to describe the collections of the

artists’ works. The famous architect Michelangelo

Buonarroti (1475-1564) once presented his portfolio

of works for an hospital for confirmation (Christensen,

2012). However, nowadays portfolios are mostly

described as a combination of different assets like

derivatives, bonds and real estate. For each asset,

there exists its return and risk. Therefore, for the

investors, the objective is to either minimize risk or

maximize total return when ceteris paribus.

Especially in 1952, Harry Markowitz first transferred

the concept into a mathematical problem and

proposed the portfolio theory in Markowitz model

(Markowitz, 2019). In the early theory, returns were

represented as 𝑟=

∑

𝑤



𝑟







where w represents for

the weight of each asset in the portfolio and the risk

as 𝑅= 𝐸



𝑟−𝐸



𝑟









. In Markowitz model,

returns and risks are shown as the following formulae

(w and r are in vector forms, and Σ is a variance

covariance matrix):

Return = 𝑤



𝑟 (1)

𝑅𝑖𝑠𝑘= 𝑤



Σ𝑤 (2)

Harry Markowitz converts the portfolio management

as an optimization problem as an equation like this.

𝑚𝑎𝑥



𝑤



𝑟−





𝑤



∑

𝑤 (3)

The model aims to seek the balance between return

and risk, which of the relationship can also be

described as the Sharpe Ratio. Despite this,

inefficiency still existed in the model. The non

negligible fact is that those investors aren’t always

risk-averse as well as their expected return won’t

always be the highest (Ban et al, 2016; Best, 2010;

Fabozzi et al, 2007).

Wang, J.

Portfolio Construction Based on LSTM RNN and Black-Litterman Model: Evidence from Yahoo Finance.

DOI: 10.5220/0013225400004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 337-343

ISBN: 978-989-758-726-9

337

The portfolio theory was developed ever since.

And in 1992, Fisher Black and Robert Litterman put

forward the Black-Litterman Model (BL model)

(Black & Litterman, 1992a; Black & Litterman,

1992b; Jorion, 1992). The BL model is an asset

allocation model that combines investors’ views on

the market with the equilibrium portfolio implied by

the market's risk and return characteristics (Gunjan &

Bhattacharyya, 2023). It adjusts the market

equilibrium using the investor's views to create a new

expected return for each asset, which is then used to

optimize the portfolio allocation. This enables

investors to factor their personal opinions about how

the market will behave in the future into their

investment choices. Matrix P represents for the map

of investors’ views to assets (He & Litterman, 2002).

Vector Q represents for actual views. Matrix Ω is an

uncertainty matrix. Nevertheless, BL model yet is not

perfect nor complete, that it is defective in several

aspects as follows (Walters, 2014):

 Subjectivity. The model requires subjective

inputs from the user, such as views on expected

returns and the choice of risk aversion

parameters. This subjectivity can lead to bias

and errors in the results.

 Data sensitivity. The covariance matrix and

expected returns are two examples of the input

data that the model is extremely sensitive to, and

even slight changes in these inputs can have a

big impact on the allocation outcomes.

 Complexity. The model is complex and requires

a deep understanding of financial markets and

investment theory in order to use it effectively.

This complexity can make it difficult for less

experienced users to implement the model

correctly.

 Lack of historical validation. The model is

based on forward-looking views and

expectations, which may not be accurately

reflected in historical data. This can lead to the

model producing unrealistic or unreliable

allocations.

 Limited application. The model is best suited for

institutional investors with access to extensive

resources and data, making it less practical for

individual or retail investors.

Due to the inefficiency and the improvement

based on previous research to BL model, the paper

aims to research on the construction of portfolios

under Markowitz model and BL model, using LSTM

model to eliminate the bias from the investors and

trying to add machine views against human views.

Hopefully, it will generate a more humanized result

according to the proportion of how the investors trust

the prediction from machines. Additionally, the

influence from the machines could be artificially

adjusted as a parameter within a specific scope

(Selvin et al, 2018).

2 DATA AND METHOD

The paper choose the history data for four

corporations from https://finance.yahoo.com: NVDA,

Apple, Intel, Google from 2023.01.01 - 2024.8.1 and

put them into the LSTM RNN for former prediction

as the machine view, and combine it with investor’s

view to verify and predict the future value of each

stock. This study mainly based on an improved BL

model, associated with LSTM model. To be specific,

it will be dealing with the Omega Matrix in the BL

model, in which interfered with the machine view to

combine with the investors’ view.

The modified model addresses the issue of having

to make a return assumption for an asset when no

historical data is available. The model initially

specifies the mean together with covariance matrix of

expected returns based on the market equilibrium.

The formulas for the mean-variance optimization are

as minimize w'Σ𝑤and subject to 𝑤′𝜇= 𝑅. Here, w is

the weight of the assets in vector form; μ represents

for the expected returns in vector form; Σ is the

covariance matrix; R is the targeted return. The

modified model then incorporates the investor's

subjective views through a Bayesian adjustment

process. The equation to calculate the adjusted

expected returns is:

𝐸

∗

= Σ((Σ



+ 𝑃′𝑄



𝑃)



)(Σ



𝐸+ 𝑃′𝑄



𝑄) (4)

Where E* is the adjusted expected return; Σ is the

covariance matrix; P is the matrix mapping the

expected returns to the views; Ω is the covariance

matrix of the errors in the views and Q is the vector

of views. Finally, the model suggests the computation

of the new optimized portfolio weights using the

adjusted expected returns and the covariance matrix.

Recurrent neural network (RNN) architectures

such as Long Short-Term Memory (LSTM) are

specifically created to solve the vanishing gradient

issue that can arise with conventional RNN. RNN'

capacity to identify long-range dependencies in

sequential data may be constrained by the vanishing

gradient problem.

LSTM networks consist of memory cells that are

connected through special gates. By controlling the

information entering and leaving the memory cells,

these gates enable the network to store and recall data

as needed. The input gate, forget gate, and output gate

are the three primary gates in an LSTM network.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

338

The forget gate regulates the amount of data that

is eliminated from the cell state, whereas the input

gate regulates the amount of new information that is

added to the cell state. The quantity of data

transferred to the network's subsequent layer is then

controlled by the output gate.

For experiment steps, one first trains the LSTM

model on historical asset prices to predict future

returns and extracts the predicted returns for the

relevant assets. Then, this study will treat the LSTM

predictions as views on expected returns for the assets.

Construct the Omega matrix based on the confidence

in the LSTM predictions. For example, Omega could

be a diagonal matrix where each element corresponds

to the inverse of the variance of the LSTM prediction

errors. Subsequently, this research will Combine the

equilibrium returns (from a market capitalization-

weighted portfolio) with the LSTM-based views,

weighted by the Omega matrix, to derive the posterior

expected returns. Finally, this paper will use the

posterior expected returns to optimize the portfolio,

typically using mean-variance optimization.

To assess the performance of the BL model and

the LSTM RNN in portfolio optimization and

forecasting, one evaluated both models using

historical market data from 2023.01.01 to 2024.08.27.

The primary metric for evaluation include the

comparison and combination of Omega Matrix which

represent the uncertainty and confidence of an

investor and the machine view generated by the

model. While the BL model excels in portfolio

optimization with a robust risk-adjusted return, the

LSTM RNN outperforms in price prediction accuracy.

However, the LSTM RNN's performance may vary

significantly due to the choice of hyper-parameters

and the volume of training data. The omega matrix is

a key parameter in the BL model, which is used to

incorporate the investor's confidence in the

equilibrium market returns. It represents the

uncertainty or in another way, the confidence in the

market equilibrium returns and is typically derived

from the investor's views or historical data. The

omega matrix helps to adjust the variance of the

equilibrium returns and influences the overall

portfolio weights. A higher value in the omega matrix

indicates higher uncertainty or lower confidence in

the equilibrium returns, which can lead to a higher

adjustment in the portfolio weights.

3 RESULTS AND DISCUSSION

This section presents the performance of the BL

model and LSTM RNN on the chosen data set from

four corporations in four different parameters in

omega matrix of investor’s view which represents

how the investors believe in machine prediction. The

metrics used for evaluation include the Omega matrix,

which is constructed as a diagonal matrix, with

elements derived from the variance of the LSTM

prediction errors. The results are shown in Figure. 1,

Figure. 2, Figure. 3 and Figure. 4 for Microsoft, Intel,

Apple and NVIDA, respectively.

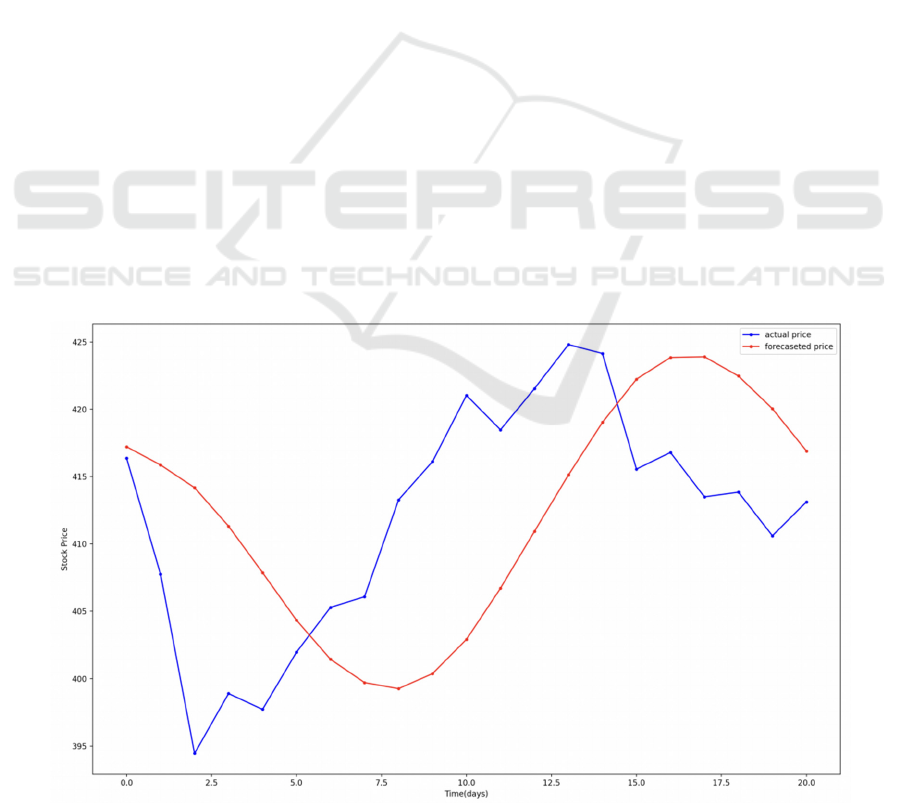
Figure 1: Results for Microsoft (Photo/Picture credit: Original).

Portfolio Construction Based on LSTM RNN and Black-Litterman Model: Evidence from Yahoo Finance

339

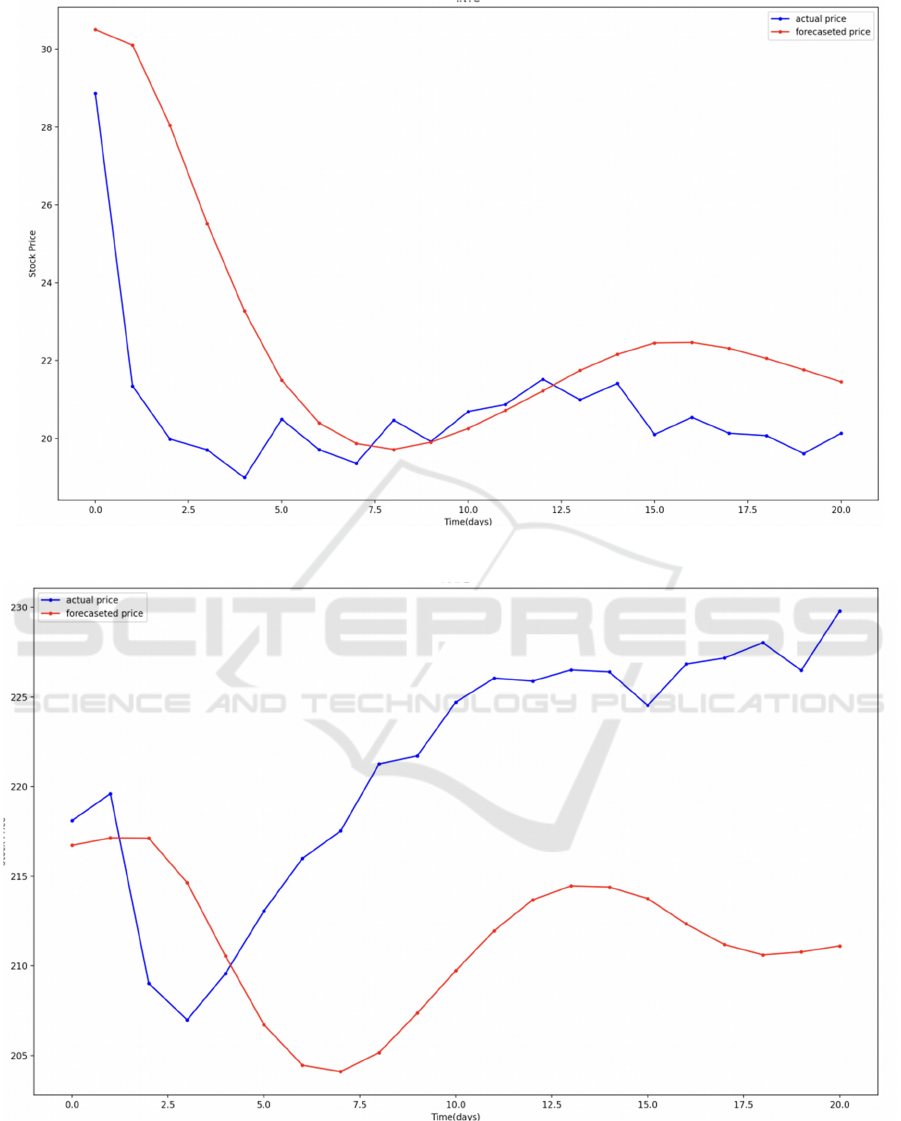
Figure 2: Results for Intel (Photo/Picture credit: Original).

Figure 3: Results for Apple (Photo/Picture credit: Original).

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

340

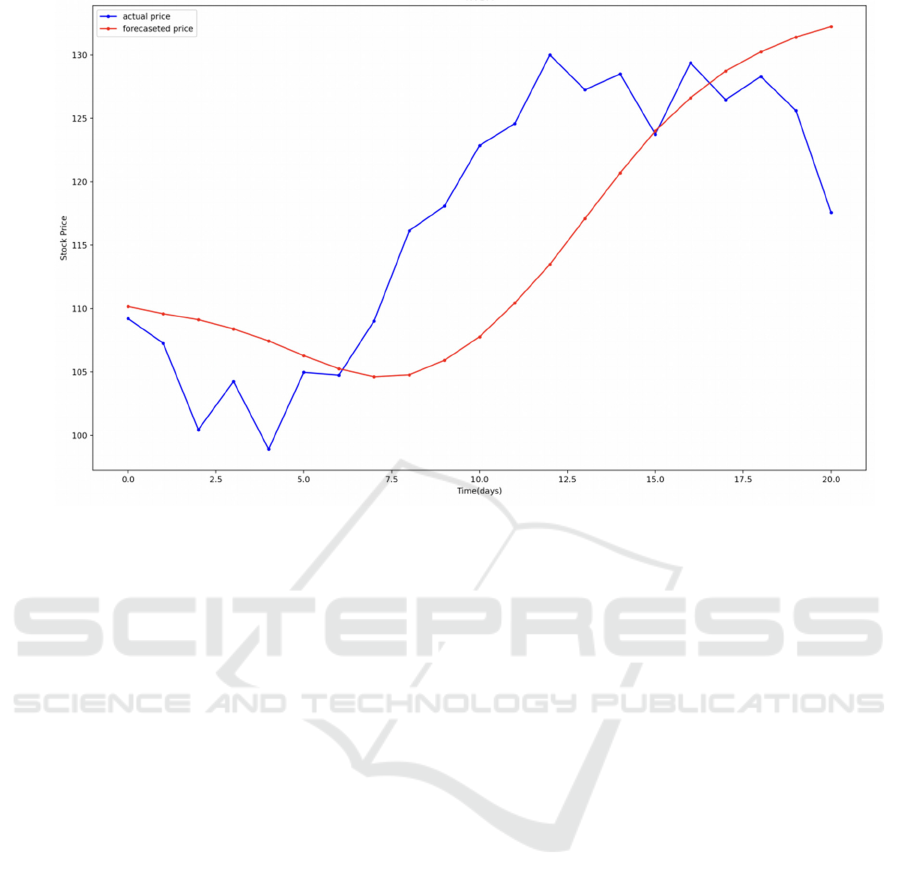
Figure 4: Results for NVIDIA (Photo/Picture credit: Original).

First of all, the results shown in Figures represents

for the LSTM RNN training results based on the

historical data from four corporations(Apple,

Microsoft, Intel, NVIDIA) from 2023.1.1 to 2024.8.1

and the prediction period is 30 days in August. The

blue fold line is the real time market trend while the

red one shows the forecast prices. Despite exhibiting

varying degrees of deviation and offset, the LSTM

model was well learned from the past market situation

and performed approximately similar trend lines as it

could be seen from the chart. Further correction and

modification against these deviations and bias ought

to be taken into consideration. Next, one views and

the Omega matrix are constructed as the confidence

and the uncertainty. The prediction from the LSTM

RNN would be treated as views on expected returns,

machine views in another word. The formats are as

follows:

𝑄



= Prediction Returns =

⎝

⎜

⎛

𝑟





𝑟





𝑟





𝑟





⎠

⎟

⎞

(5)

𝑄



=Investor View =

⎝

⎜

⎛

𝑟





𝑟





𝑟





𝑟





⎠

⎟

⎞

(6)

This study adds the investors’ views as Q2 to the

machine prediction and modify the proportion of each

views to combine and forms a integrated view as the

views Matrix Q. Together with the Omega matrix

constructed from the variance of each historical error,

one would apply it to the BL model to combine with

the LSTM predicted returns, weighted by the Omega

matrix. Finally, it Optimize Portfolio Using the

posterior expected returns, mean-variance

optimization are performed to build an optimized

portfolio. The analysis revealed that the LSTM model

exhibited a certain degree of bias and deviation in its

stock price predictions. The model consistently

overestimated or underestimated the actual stock

prices, leading to relatively high MAE and RMSE

values. Furthermore, the model's predictions showed

a tendency to deviate from the actual stock price

trends, particularly in the presence of sudden market

fluctuations or anomalies. These findings indicate

that the presence of bias and deviation can

significantly affect the accuracy and reliability of the

LSTM RNN for stock prediction.

The presence of bias and deviation in the LSTM

model's stock predictions has important implications

for its practical utility in financial markets. Inaccurate

predictions can lead to substantial financial losses for

investors and traders, and undermine the trust and

credibility of the model as well. Therefore, it is

crucial to mitigate bias and deviation in the model's

predictions through the use of advanced

Portfolio Construction Based on LSTM RNN and Black-Litterman Model: Evidence from Yahoo Finance

341

regularization techniques, feature engineering, and

data preprocessing methods. Additionally,

transparency and interpretability in the model's

decision-making process are essential for building

confidence in its predictions and insights.

The BL model provides a more realistic and

robust allocation of the portfolio by accounting for

both the market equilibrium and the subjective

opinions of the investor. The model enables a more

specialized and customized portfolio that is in line

with the investor's objectives and risk tolerance by

taking into account the investor's opinions. The

implication is that the portfolio generated using BL

model has a higher chance of fulfilling the demands

and expectations of the investor. After implementing

the BL model and generating the portfolio, we could

conducted a back test analysis to evaluate its

performance. The portfolio was compared to a

standard market benchmark to assess its risk-adjusted

returns and volatility. Additionally, this research

examined the portfolio's reaction to shifts in the

market as well as the effect of investor opinions on

portfolio allocation.

Combining the LSTM RNN predictions with the

Omega matrix from the BL model offers a novel

approach to portfolio optimization, but it is not

without limitations. One key limitation lies in the

estimation of the Omega matrix. The Omega matrix,

which represents the uncertainty in the LSTM

predictions, is often constructed using the variance of

prediction errors. However, accurately estimating

these variances can be demanding, especially in

volatile markets or when working with limited

historical data. Misestimation of the Omega matrix

could lead to overconfidence in the LSTM predictions,

resulting in sub-optimal portfolio allocations.

Another limitation is the inherent complexity of the

combined model. Integrating LSTM RNN predictions

into the Black-Litterman framework requires careful

calibration and understanding of both models'

mechanics. The complexity may make it difficult for

practitioners without advanced technical expertise to

implement and interpret the results correctly.

Moreover, the LSTM model, being a data-driven

approach, is highly dependent on the quality and

quantity of the input data. Inaccurate forecasts

resulting from inadequate or poor quality data can

impact views and ultimately the performance of the

portfolio. The computational demands of training

LSTM models and running the Black-Litterman

optimization are also non-trivial. These models

require significant computational resources,

particularly when working with sizable datasets or

asset-rich portfolios. This can be a barrier for smaller

institutions or individual investors with limited access

to high-performance computing resources.

Despite these limitations, the combination of

LSTM RNN predictions and the Omega matrix from

the Black-Litterman model holds significant potential

for future development. One promising area is the

refinement of the Omega matrix estimation.

Advanced methods could be explored to better

capture the uncertainty in the LSTM predictions (e.g.,

Bayesian approaches or machine learning techniques),

leading to more robust portfolio allocations. Another

prospect lies in enhancing the interpretability of the

combined model. A wider range of users may find the

model more approachable if more natural ways to see

and understand the relationships between the BL

model outputs and the LSTM predictions were

developed. Additionally, integrating alternative

machine learning models with the Black-Litterman

framework could be explored. Models like

Transformers or reinforcement learning-based

approaches might offer improvements in prediction

accuracy and decision-making under uncertainty.

Finally, as computational resources continue to

advance, the practical barriers to implementing

complex models like this one will diminish, making

it more feasible for a wider range of practitioners.

This could lead to broader adoption and further

refinement of the model in real-world portfolio

management scenarios, ultimately improving

investment outcomes in a dynamic and uncertain

financial environment.

4 CONCLUSIONS

To sum up, this study explores the integration of

LSTM RNN predictions with the BL model to

enhance portfolio optimization. Results demonstrate

that incorporating LSTM RNN predictions into the

BL model framework can mitigate biases and offer a

more refined approach to asset allocation. While the

LSTM model improves forecasting accuracy, it

introduces biases that require careful calibration. The

modified Black-Litterman model, combining

machine and investor views, provides a more tailored

portfolio allocation but demands significant

computational resources and expertise. Future

research could focus on refining the Omega matrix

estimation and exploring alternative machine

learning models to further improve robustness. This

research advances the understanding of combining

machine learning with traditional financial models,

offering a novel approach to enhance portfolio

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

342

management and decision-making in a dynamic

market environment.

REFERENCES

Ban, G. Y., El Karoui, N., Lim, A. E. B., 2016. Machine

learning and portfolio optimization. Management

Science, 2644.

Best, M. J., 2010. Portfolio optimization. CRC Press.

Black, F., Litterman, R., 1992a. Global portfolio

optimization. Financial Analysts Journal, 48(5), 28–43.

Black, F., Litterman, R., 1992b. The Black–Litterman

model explained. Journal of Asset Management, 11(3),

229–243.

Christensen, M. M., 2012. On the history of the growth-

optimal portfolio. Growth optimal portfolio, 3-30.

Fabozzi, F. J., Kolm, P. N., Pachamanova, D. A., Focardi,

S. M., 2007. Robust portfolio optimization and

management. John Wiley & Sons.

Gunjan, A., Bhattacharyya, S., 2023. A brief review of

portfolio optimization techniques. Artificial

Intelligence Review, 56, 3847–3886.

He, G., Litterman, R., 2002. The intuition behind Black-

Litterman model portfolios. Goldman Sachs Group, Inc.,

Quantitative Strategy Group; Kepos Capital.

Jorion, P., 1992. Portfolio optimization in practice.

Financial Analysts Journal, 48(1), 68–74.

Markowitz, H. M., 2019. The early history of portfolio

theory: 1600–1960. Financial Analysts Journal, 55(4),

5-16.

Selvin, S., Vinayakumar, R., Gopalakrishnan, E. A., Menon,

V. K., Soman, K. P., 2017. Stock price prediction using

LSTM, RNN and CNN-sliding window model. IEEE.

Walters, J., 2014. The Black-Litterman model in detail.

Boston University, Metropolitan College, Department

of Computer Science.

Portfolio Construction Based on LSTM RNN and Black-Litterman Model: Evidence from Yahoo Finance

343