Stock Price Prediction Based on SDE and LSTM: Evidence from BYD

Yaling Xu

School of International Education, Guangdong University of Technology, Guangzhou, China

Keywords: Long Short-Term Memory, Stochastic Differential Equation, Stock Market, Price Prediction.

Abstract: With the increasing complexity and dynamism of the stock market, traditional forecasting methods make it

difficult to accurately capture market fluctuations. In recent years, deep learning models have gradually been

applied to the stock market, demonstrating superior research results. This article investigates a stock price

prediction model based on the combination of Long Short-Term Memory (LSTM) and Stochastic Differential

Equations (SDE). The model utilizes the excellent time series processing capability of LSTM and the

advantage of SDE in describing stochastic processes, which can improve the prediction accuracy of stock

prices. This article concludes that by introducing SDE, the model can better simulate the randomness and

volatility of stock prices, while LSTM effectively captures long-term and short-term dependencies in

historical data. With machine learning models can be explored to enhance the real-time performance and

adaptability of the models. In addition, this study only considered the price prediction and simulation of a

single stock, the experimental results show that the LSTM-SDE model has good predictive performance in

stock price prediction and can provide investors with more reliable decision support.

1 INTRODUCTION

Stock price prediction is a complex and dynamic

research field that covers multiple disciplines such as

economics, finance, statistics, and computer science.

Researchers hope to use scientific research methods

to predict the price trends of stocks. Stock price

prediction, as one of the core issues in financial

market analysis, has gone through multiple stages of

development. The research on stock price prediction

has undergone an evolution from classical theory to

modern data-driven models.

In the early days of the stock market, Graham and

Dodd analyzed the reasons for the 1929 US stock

market price crash in their book "Securities Analysis"

and believed that stock price fluctuations were based

on the "intrinsic value" of stocks. This viewpoint

provided an important theoretical basis for later stock

price predictions.

At the beginning of the 20th century, stock price

prediction mainly relied on fundamental analysis,

which evaluated the intrinsic value of stocks by

analyzing factors such as a company's financial

statements, industry position, management team,

market competitiveness, and macroeconomic

https://orcid.org/0009-0007-1913-3611

indicators. Investors would decide whether to invest

based on these fundamental analyses. The early

research on the stock market was mainly based on the

Random Walk Theory. Fama discussed the theory of

random walks and believed that the price level of

future path securities is not easy to predict, and

market price changes are unpredictable (Fama, 1965).

In 1970, Fama proposed the Efficient Market

Hypothesis, which states that the good functioning,

competitive nature, and high profits of the stock

market allow everyone to try to predict stock prices,

and all valuable information can be reflected in stock

price trends in a timely, accurate, and sufficient

manner, which also means that stock prices are

difficult to predict (Fama, 1970).

With the advancement of technology and the

improvement of data processing capabilities,

researchers have begun to search for more complex

models to predict stock prices. Since the 1970s,

research methods have gradually shifted towards time

series analysis, machine learning, and deep learning.

Box and Jenkins proposed the Autoregressive

Integrated Moving Average (ARIMA) model, which

can be used for predicting time series data (Box &

Jenkins, 2015). Bollerslev introduced the Generalized

Xu, Y.

Stock Price Prediction Based on SDE and LSTM: Evidence from BYD.

DOI: 10.5220/0013213100004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 209-213

ISBN: 978-989-758-726-9

209

Autoregressive Conditional Heteroskedasticity

(GARCH) model for handling volatility in financial

data (Bollerslev, 1986). Entering the 21st century,

with the rise of machine learning and artificial

intelligence technologies, new tools have been

provided for stock price prediction. Kim introduced

SVM into financial market forecasting,

demonstrating the potential of the model in nonlinear

data processing and prediction (Kim, 2003). Deep

learning models have gradually been applied to

financial markets. Fischer and Krauss (2018) used

Long Short-Term Memory networks (LSTM) to

predict financial markets, demonstrating the

application ability of deep learning models in

complex time series (Fischer & Krauss, 2018).

In recent years, Zhang combined neural networks

with ARIMA models to propose a hybrid model for

predicting stock prices, which significantly improved

prediction accuracy (Zhang, 2003). Dang applied

reinforcement learning (RL) to optimize trading

strategies in dynamic environments, demonstrating

good adaptability (Dang, 2019). In addition,

researchers combined Convolutional Neural

Networks (CNN) with LSTM, utilizing the advantage

of CNN in extracting local features from time series,

and processed these features with LSTM to generate

prediction results (Eapen et al., 2019).

With the development of natural language

processing technology, Vaswani applied the

Transformer model to stock price prediction and

found that it can further improve the ability to capture

complex data patterns (Vaswani, 2017). More

cutting-edge applications include Graph Neural

Networks (GNNs), which can effectively capture the

relationships between stocks and improve market

prediction accuracy (Chen et al., 2023).

2 DATA AND METHOD

To analyse the actual performance of the LSTM-SDE

model in stock prediction, daily individual stock

return data of BYD from August 26, 2019, to August

23, 2024, were downloaded from CSMAR, and daily

closing prices for the past five years were extracted

from it.

2.1 Data

The data for this analysis is sourced from the China

Stock Market & Accounting Research Database

(CSMAR), which has authoritative sources including

the Hong Kong Stock Exchange, China International

Capital Exchange, the State Administration of

Foreign Exchange, and so on, ensuring the accuracy

and authority of the data.

The dependent variable is the dependent variable

is BYD's daily closing price while independent

variables are predicts future prices, predicting the

daily closing price for a certain period. The collected

dataset is separated into training and testing sets to

ensure the model's generalization ability. The training

set is used for the model's training process, that is, to

learn the inherent rules and patterns of the data; The

test set is used to appraise the final performance of the

model, ensuring that it can perform well on unseen

data. Therefore, the top 80% of the overall data will

be used as the training set, which includes data from

August 26, 2019, to August 23, 2023; The remaining

20% of the data will be used as the test set from

August 24, 2023 to August 23, 2024. In the data

preprocessing stage, the closing price-related data of

the corresponding time and date of the stock were

extracted. After normalizing the data, it was separated

into training and testing sets. At the same time, the

data was processed accordingly, such as processing

the text or missing values in the closing price and

extracting the remaining readable data to provide

correct data for subsequent model training and

prediction.

2.2 Models

In the BYD stock prediction task, this article uses the

LSTM model and SDE model. The LSTM model is

used for time series prediction to obtain the initial

intermediate variable z_0, which is used in the SDE

model to simulate the path of stock prices. The

process includes Data normalization and extraction of

closing price features; Slice the data into training and

testing sets; Extract data that can be read correctly

from the data. For LSTM model training, in the first

half of the process, an LSTM network was

constructed to process sequence data, initial

intermediate variables were obtained through inverse

normalization, and mean square error was collected.

Train the model by providing training set data,

training epochs, batch size, and validation set

segmentation ratio to minimize the mean square error

between predicted and actual values. As for model

validation, one uses 10% of the training set as the

validation set to evaluate its performance and prevent

overfitting. Regarding to SDE model design, based on

the initial intermediate variable z-0 predicted by

LSTM, multiple stock price paths were simulated

using the SDE model, and the drift term μ and

diffusion term σ were calculated in the model for

subsequent SDE model construction. For model

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

210

evaluation, this study will calculate the root mean

square error (RMSE) between the actual price and the

predicted price (LSTM) and the SDE simulation path.

For LSTM model parameters, this study designed

two layers of LSTM. The number of LSTM units per

layer is 50; Using optimizer Adam, it can be used to

adjust the learning rate automatically; using mean

square error as the loss function. The entire dataset

has 50 training epochs. Each gradient update will use

32 samples for calculation. This study set aside 10%

of the training data as the validation set for evaluating

model performance during the training process. For

SDE model parameters, one designed a drift term (μ)

for the logarithmic rate of return calculation.

Diffusion term (σ) is used for calculating the standard

deviation of logarithmic returns. The time step (dt) is

1 day and one designs 10 simulated paths (sim_time).

The project uses Model Discussion Root Mean

Square Error (RMSE) to evaluate the quality of the

model. Used to evaluate the difference between

LSTM model predicted prices and actual prices, as

well as the difference between SDE simulated path

mean and actual prices. The smaller the RMSE value,

the better the model's prediction or simulation

performance.

3 RESULTS AND DISCUSSION

3.1 Model Performance

This study combined the LSTM neural network and

stochastic differential equation (SDE) model to

predict stock prices and conducted a detailed analysis

of the results. The LSTM model has demonstrated

strong capabilities in capturing complex dynamic

features of time series data, especially when dealing

with nonlinear and non-stationary data such as stock

prices. By setting appropriate time steps

(time_step=60) and training parameters (such as

epochs=50, batch_2=32), the LSTM model

successfully learned patterns in the stock price

sequence and provided relatively accurate predictions

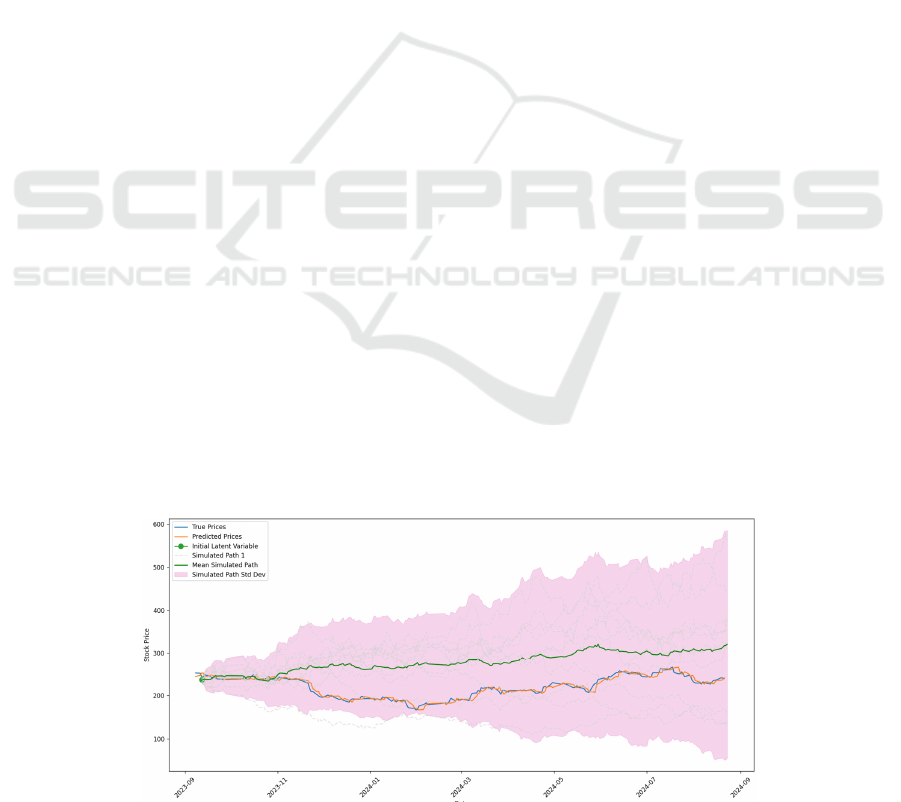
on the test set. The prediction results are shown in Fig.

Specifically, the continuous decrease in the loss of

LSTM models on the training and validation sets

indicates that the model is learning the intrinsic

patterns of the data. After 50 training cycles, the

LSTM model's predicted stock price trend maintained

good consistency with the real stock price, especially

in capturing trends accurately. However, in predicting

short-term fluctuations and extreme values, the

performance of the LSTM model is slightly

inadequate. This may be because of the complexity

and uncertainty of the stock market, which is

influenced by various external factors including

policy changes, market sentiment, etc. These factors

are difficult to fully quantify and incorporate into the

model. Therefore, there is still a certain degree of

error in the prediction results of the LSTM model.

Compared with the LSTM model, the SDE model

exhibits unique advantages in simulating the long-

term dynamics and uncertainty of stock prices and

provides multiple possible paths for future price

trends. The SDE model simulates the stochastic

process of stock prices, displays the possible range of

stock price fluctuations, and quantifies uncertainty by

calculating the mean path and standard deviation. In

the visualization results, one can see that the average

path simulated by SDE is consistent with the real

price trend, indicating that the SDE model has certain

effectiveness in capturing the long-term trend of stock

prices. At the same time, the setting of confidence

intervals also provides us with a visual understanding

of prediction uncertainty. However, the predictive

ability of SDE models for short-term fluctuations is

relatively weak, which may be due to the deviation

between their assumptions based on statistical

distribution and the actual situation.

Figure 1: The prediction results (Photo/Picture credit: Original).

Stock Price Prediction Based on SDE and LSTM: Evidence from BYD

211

3.2 Explanation

The LSTM model performs well in stock price

prediction, mainly due to the design of its internal

loop unit (LSTM unit), which enables LSTM to

selectively retain and forget information. These

mechanisms effectively capture long-term

dependencies in time series data and control the flow

of information through mechanisms such as forget

gates, input gates, and output gates. In this study, by

setting appropriate time steps and number of neurons,

the LSTM model successfully extracted useful

features from historical price data, continuously

learned patterns from historical stock price data, and

gradually developed the ability to predict stock price

trends. However, stock prices are not only influenced

by historical data in real life but also by many

unpredictable external factors. These external factors

may cause significant fluctuations in stock prices in

the short term, exceeding the prediction range of the

LSTM model. In the stock market, it is influenced by

numerous macro and micro factors, and the

interaction between these factors makes the changes

in stock prices highly complex and uncertain.

Therefore, even if the LSTM model can capture some

historical patterns, it is difficult to accurately predict

future stock prices. In addition, LSTM models may

overfit the noise in the training data during the

training process, which can affect their performance

on the test set.

The SDE model predicts future trends by

simulating the stochastic process of stock prices. In

this study, the drift term (μ) and diffusion term (σ)

were calculated based on historical price data. In the

SDE model, the drift term represents the expected

trend of stock prices, while the diffusion term

represents the magnitude of price fluctuations. By

adjusting these two parameters, the SDE model

generated multiple simulated paths and quantified

uncertainty by calculating the average path and

standard deviation. The characteristic of the SDE

model gives it a unique advantage in handling

financial time series data with uncertainty. However,

the prediction accuracy of the SDE model is also

affected by various factors, such as the accuracy of

parameter estimation, the rationality of model

assumptions, and changes in the market environment.

3.3 Limitations and Prospects

Although this study has shown good performance in

combining LSTM and SDE models for stock price

prediction, the model still has some limitations. Due

to limitations in model structure and training data,

LSTM models have limited ability to capture short-

term fluctuations and extreme values. In the future,

more feature variables such as trading volume and

market sentiment can be considered to strengthen the

predictive ability of the model.

Although the SDE model can simulate the

uncertainty of stock prices, its parameters, namely

drift and diffusion terms, depend on the statistical

characteristics of historical data, and are trained and

predicted based on historical data. It may not fully

capture the changes in the market environment and

the impact of unexpected events on stock prices in the

future market. Therefore, in future research, more

flexible and dynamic parameter estimation methods

can be attempted to improve the prediction accuracy

of SDE models, or methods that combine real-time

data, news sentiment analysis, and other technologies

with machine learning models can be explored to

enhance the real-time performance and adaptability

of the models. In addition, this study only considered

the price prediction and simulation of a single stock,

and in practical applications, investors may be more

concerned with the performance of multiple stocks or

the entire market combination, as well as other factors

that may affect stock price changes, such as

macroeconomic indicators, company financial

conditions, etc. Therefore, in the future, this research

method can be extended to areas such as correlation

analysis in multi-asset or multi-market situations, or

more related variables can be introduced as feature

inputs. This will help to comprehensively understand

the operating rules of the stock market, improve the

prediction accuracy and generalization ability of the

model, provide more comprehensive and practical

prediction results, and provide investors with more

accurate and valuable decision support.

As a result of the progression of the continuous

development of artificial intelligence and big data

technology, more advanced algorithms and

technologies can be considered to be introduced into

the field of stock price prediction in the future. For

example, attention mechanisms in deep learning can

be utilized to strengthen the model's focus on

important information; Or use reinforcement learning

to optimize trading strategies to achieve higher

investment returns. The application of these new

technologies is expected to further enhance the

accuracy and practicality of stock price forecasting.

4 CONCLUSIONS

To sum up, this study delves into the application of

the LSTM-SDE model in stock price prediction and

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

212

verifies its effectiveness and superiority through

empirical analysis. Research has found that the

LSTM-SDE model can fully utilize historical data in

the stock market, and capture market trends through

the memory mechanism of LSTM, and the

introduction of SDE further enhances the model's

ability to capture random fluctuations in stock prices.

Compared to a single LSTM model, LSTM-SDE

performs well in both prediction accuracy and

stability. However, this article also points out the

limitations of the model in practical applications,

such as the need to rely more on historical data and

introduce more feature variables. Future research can

further explore how to optimize model structure,

improve computational efficiency, and consider

introducing more external factors to further enhance

prediction performance. In summary, the LSTM-SDE

model provides a new approach and method for stock

price prediction, with high potential for application

and research value.

REFERENCES

Bollerslev, T., 1986. Generalized Autoregressive

Conditional Heteroskedasticity. Journal of

Econometrics, 31(3), 307-327.

Box, G. E., Jenkins, G. M., Reinsel, G. C., Ljung, G. M.,

2015. Time series analysis: forecasting and control.

John Wiley & Sons.

Chen, Z., Huang, Z., Zhou, Y., 2023. Predicting Stock

Trend Using GNN. Highlights in Science, Engineering

and Technology, 39, 816-822.

Dang, Q. V., 2019. Reinforcement learning in stock trading.

International conference on computer science, applied

mathematics and applications 311-322.

Eapen, J., Bein, D., Verma, A., 2019. Novel deep learning

model with CNN and bi-directional LSTM for improved

stock market index prediction. 2019 IEEE 9th Annual

Computing and Communication Workshop and

Conference (CCWC), 264-270.

Fama, E. F., 1965. The Behaviour of Stock-Market Prices.

The Journal of Business, 38(1), 34–105.

Fama, E. F., 1970. Efficient Capital Markets: A Review of

Theory and Empirical Work. The Journal of Finance,

25(2), 383–417.

Fischer, T., Christopher, K., 2018. Deep learning with long

short-term memory networks for financial market

predictions. European Journal of Operational Research,

270(2), 654-669.

Kim, K. J., 2003. Financial time series forecasting using

support vector machines. Neurocomputing, 55(1-2),

307-319.

Vaswani, A., 2017. Attention is all you need. Advances in

Neural Information Processing Systems.

Zhang, G. P., 2003. Time series forecasting using a hybrid

ARIMA and neural network model. Neurocomputing,

50, 159-175.

Stock Price Prediction Based on SDE and LSTM: Evidence from BYD

213