Prediction of DOGE Based on Random Forest, Long Short-Term

Memory and Transformer

Shengjie Yu

Department of Computer Science and Technology, Nanjing University, Nanjing, China

Keywords: Dogecoin Price Prediction, Machine Learning, Random Forest, LSTM, Transformer.

Abstract: As cryptocurrencies have surged in value and importance in recent years, Dogecoin has been increasingly

regarded as an investment asset. Due to its high volatility, the demand to forecast Dogecoin prices using

machine learning techniques is rising. This study explores the application of four models, i.e., Linear

Regression, Random Forest, Long Short-term Memory (LSTM), and Transformer, in forecasting the hourly

prices of Dogecoin. Through comprehensive experiments, using MAE, MSE, and R-squared data as test

standards, the LSTM model demonstrated superior performance, achieving the lowest error rates compared

to the other models, followed by the linear regression model. The Random Forest model also performed

reasonably well but fell short of the linear regression model. The Transformer model, despite its advanced

architecture, delivered the poorest performance, highlighting its limitations in this specific time series

forecasting task. These findings suggest that LSTM models may be more effective for time series prediction

tasks in the cryptocurrency market, highlighting the need for further research into advanced machine learning

techniques for financial forecasting.

1 INTRODUCTION

Cryptocurrency traces its origins back to 2008 when

a developer under the pseudonym Satoshi Nakamoto

published the white paper. In 2009, the Bitcoin

network was officially launched, marking the birth of

the world's first decentralized cryptocurrency. In

addition to reducing transaction fees,

cryptocurrencies aim to provide consumers with more

control over their finances (Sridhar & Sanagavarapu,

2021). These currencies' high accessibility which

prevents the publication of private information and

allows for traceability has allowed them to flourish

over time. Cryptocurrencies went from relative

obscurity to a peak worldwide market value of over

$3 trillion in the previous ten years (Singla et al.,

2024). Dogecoin is one such cryptocurrencies that has

gained growing popularity.

Dogecoin, created by Billy Markus and Jackson

Palmer, is a cryptocurrency that originated as a

derivative of Bitcoin and was introduced on

December 6, 2013, as a joke or meme currency

(Sridhar & Sanagavarapu, 2021). Technically,

Dogecoin shares many similarities with Bitcoin, but

its inflationary mechanism is different. As opposed to

the limited supply of Bitcoin, Dogecoin was designed

to have an unlimited supply, allowing new Dogecoins

to be continuously generated (Chohan, 2021). Like

other cryptocurrencies, Dogecoin has proven to be

highly volatile (Zhang and Mani, 2021). In 2021,

Dogecoin's market capitalization surpassed $88

billion due to a further internet-driven price surge,

with each DOGE coin valued at more than 70 cents

(Nani, 2022). As of August 12, 2024, Dogecoin's total

market capitalization has reached $14.808 billion

(Dogecoin, 2024).

Due to the significant investment value of

cryptocurrencies, there has already been extensive

research on cryptocurrency price prediction.

Aravindan et al. used the moving average to eliminate

short-term fluctuations in cryptocurrency prices,

while employing various models, including Decision

Tree, Random Forest, Extra-Tree Regressor to predict

the closing prices of cryptocurrencies (Aravindan &

Sankara, 2022). Dhande et al. estimated the values of

Bitcoin, Dash currency, Lite coin, Dogecoin,

Ethereum, and Monero, using LSTM by introducing

the "memory cell" and three gating mechanisms

(Dhande et al., 2024). Wallbridge utilized a

Transformer model to predict price movements. The

transformer model does not rely on the order of

sequential data. Instead, the model employs a

188

Yu, S.

Prediction of DOGE Based on Random Forest, Long Short-Term Memory and Transformer.

DOI: 10.5220/0013212500004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 188-194

ISBN: 978-989-758-726-9

sophisticated mechanism known as self-attention,

which is designed to effectively capture and analyze

dependencies within the data (Wallbridge, 2020). A

better PSO technique and the XGBoost method,

based on the gradient boosting framework were

integrated by Srivastava et al. to optimize the optimal

hyper-parameters (Srivastava, et al., 2023).

In this article, the author used a variety of models

to predict the price of Dogecoin. With linear

regression model as a comparison, an in-depth study

on the prediction effects of three types of models,

random forest, LSTM and transformer, was

conducted. In the process of research, MAE, MSE

and R-square were used as evaluation criteria. This

study aims to verify and improve the existing time

series forecasting model by predicting the price of

Dogecoin and use the data in this field to optimize and

adjust the model to improve the model's adaptability

to high volatility and uncertainty markets. At the

same time, by predicting the prices of

cryptocurrencies such as Dogecoin, researchers can

better understand the dynamic behavior of the

financial market and explore how to use forecasting

models for hedging, risk avoidance, and asset

allocation optimization. The rest of the paper is

organized in this manner. Particular models are

introduced and the data sources and analysis

techniques are described in the second section. The

experiment's results are presented in the third part,

which also delves further into them and discusses the

study's shortcomings as well as potential future

directions. The fourth section summarizes the whole

article.

2 DATA AND METHOD

For the research, this study utilized data from

2019/7/5 12:00:00 to 2024/8/6 16:00:00, concerning

the hourly prices of Dogecoin in USD and were

divided into a training set consisting of data from

2019/7/5 12:00:00 to 2023-08-01 22:00:00 (32552

values) and a testing set from 2023-08-01 23:00:00 to

2024/8/6 16:00:00 (8139 values). All of the data is

downloaded from the API endpoint provided by

Binance for retrieving hourly candlestick data for

cryptocurrency markets. Candlestick data displays

the open, high, low, and close prices and the trading

volume over the required time period.

To confirm that the model works as intended, it is

necessary to use appropriate testing methods to

examine the predicted results. The results are tested

with the below evaluation metrics. The average of the

absolute discrepancies between the expected and

actual values is known as the mean absolute error, or

MAE. It functions as a gauge for how closely forecast

results match actual results. Here, y represents the

actual value, 𝑦



 refers to the predicted value by the

model and n is the number of observations:

MAE =





∑ |

𝑦



−𝑦









(1)

The average of the squared discrepancies between

the expected and actual values is known as the mean

squared error, or MSE. MSE quantifies the average

size of the prediction mistakes in a model. Larger

errors are given more weight, which makes them

stand out more when evaluating the model:

MSE =





∑

𝑦



−𝑦













(2)

The percentage of the dependent variable's

variance that can be predicted from the independent

variables is expressed statistically as R-squared (R²):

𝑅



=1−

∑



















∑

















(3)

Linear regression presupposes a linear

relationship between the independent and dependent

variables, which can be represented by a hyperplane

in the case of several predictors or a straight line in

the case of one predictor. By using the least squares

method, one can discover the best-fitting line or

hyperplane in linear regression. In this set of

experiments, the linear regression model was used as

the control group.

Random Forest operates by constructing many

decision trees and making predictions based on output

of these trees. By averaging the predictions of many

trees, random forest becomes a more generalized

model. In this experiment, after repeated optimization,

the parameters are set as follows:

max_depth=8,n_estimators=90,min_samples_split=1

6,min_samples_leaf=6,oob_score=True,max_feature

s=15.

LSTM was created to solve the problems with

vanishing and exploding gradients that arise in

ordinary RNNs while working with lengthy data

sequences. It introduces three gating units (input gate,

forget gate, and output gate) and these gates help

LSTM decide which information should be

remembered, which should be forgotten, and how the

information influences the output: Input Gate

determines if the memory cell should be updated with

the current input data.

𝑖



= 𝜎



𝑊



⋅



ℎ



, 𝑥





+ 𝑏





(4)

Here, 𝑖



is the output of the input gate, 𝑊



is the

input gate's weight matrix, and 𝑏



is the input gate

bias, ℎ



is the previous hidden state, 𝑥



is the

current input. Forget Gate determines whether the

information previously stored in the memory cell

should be forgotten:

Prediction of DOGE Based on Random Forest, Long Short-Term Memory and Transformer

189

𝑓



= 𝜎𝑊



⋅



ℎ



, 𝑥





+ 𝑏



 (5)

Here, 𝑓



is the forget gate output, 𝑊



is the weight

matrix and 𝑏



is the forget gate bias. Candidate

Memory Cell can be described as:

𝐶





=tanh



𝑊



⋅



ℎ



, 𝑥





+ 𝑏





(6)

Here, 𝐶





is the candidate memory cell value, 𝑊



the weight matrix, and 𝑏



is the bias. Update Cell

State:

𝐶



= 𝑓



⋅𝐶



+ 𝑖



⋅𝐶





(7)

Here, 𝐶



is the current cell state, and 𝐶



is the

previous cell state. Output Gate:

𝑜



= 𝜎



𝑊



⋅



ℎ



, 𝑥





+ 𝑏





(8)

Here, 𝑜



is the output of output gate, 𝑊



is the

output gate's weight matrix, and 𝑏



is the output gate

bias. Update Hidden State:

ℎ



= 𝑜



⋅ tanh



𝐶





(9)

The purpose is to create the output of the LSTM

model, preserving useful information while

suppressing irrelevant information.

The self-attention mechanism of Transformer

model makes it well-suited for handling time series

data. This mechanism calculates a set of attention

weights for each input vector, focusing attention on

the sections of the sequence that matter the most. In

this experiment, a custom multi-head attention layer

was used. Multi-head attention splits the input into

multiple subspaces and performs attention

calculations independently, then combines the results.

Following the multi-head attention layer, the model

includes a dense layer with 32 units. The dense layer

further processes the output from the multi-head

attention and compresses it into a lower-dimensional

feature representation. Then, the global average

pooling layer is used to convert the sequence of

feature vectors into a single scalar by taking the

average across all time steps in the sequence. This

layer improves training efficiency and stability. It

also helps to prevent overfitting by reducing

redundant features. Finally, the model outputs a

single value through a dense layer, which represents

the predicted value for the time series. In time series

forecasting tasks, this output could be the predicted

price, temperature, or any other continuous variable

for a future time point.

3 RESULTS AND DISCUSSION

3.1 Feature Engineering

The data includes five items: opening, highest, lowest,

closing price and trading volume. The author

conducted a correlation analysis on these five items.

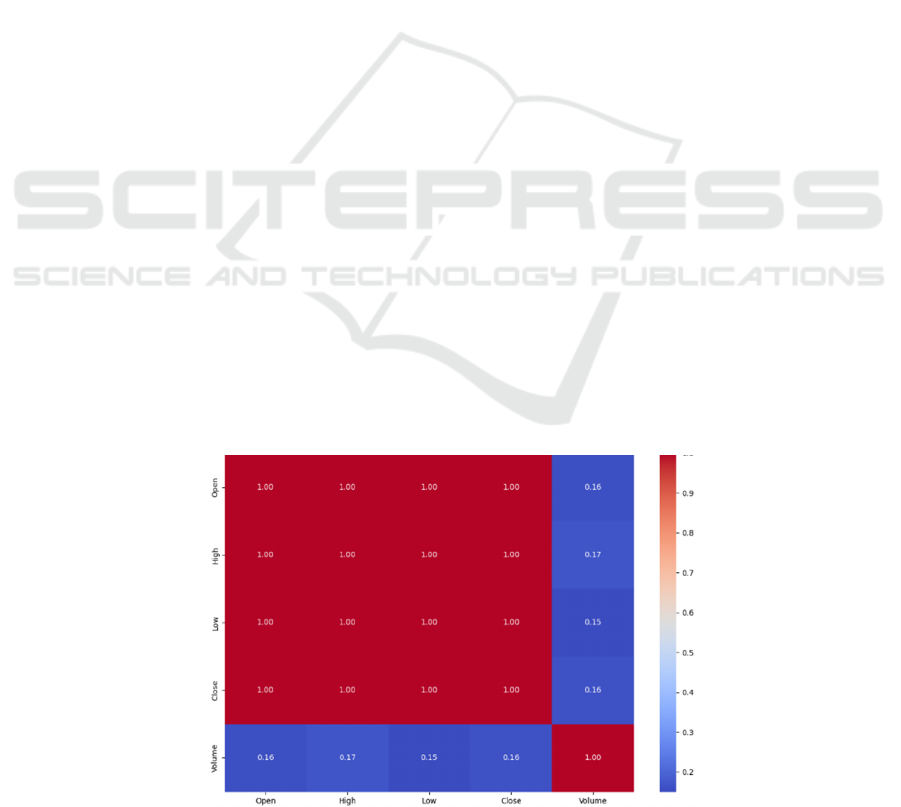
The Figure. 1 displays the findings. Seen from the

results, the Open, High, Low, and Close prices all

have a correlation coefficient of 1 with each other.

This indicates a perfect positive correlation among

these four variables, meaning that these price data

points move in tandem.

On the other hand, Volume has a lower correlation

with the price data, with correlation coefficients

ranging between 0.15 and 0.17. This shows that the

price and trading volume have a poor correlation,

meaning that there is only a weak association between

price fluctuations and trading volume in this dataset.

Since the correlation coefficients of opening,

highest, lowest and closing price are all 1, the author

deleted the three columns of opening, highest and

lowest price. Then, daily closing prices and trading

volumes are normalized to transform the time series

data into the form of a supervised learning set. For the

purpose of prediction, use 80% of the samples as the

training set and 20% as the test set.

Figure 1: Correlation analysis of DOGE Data (Photo/Picture credit: Original).

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

190

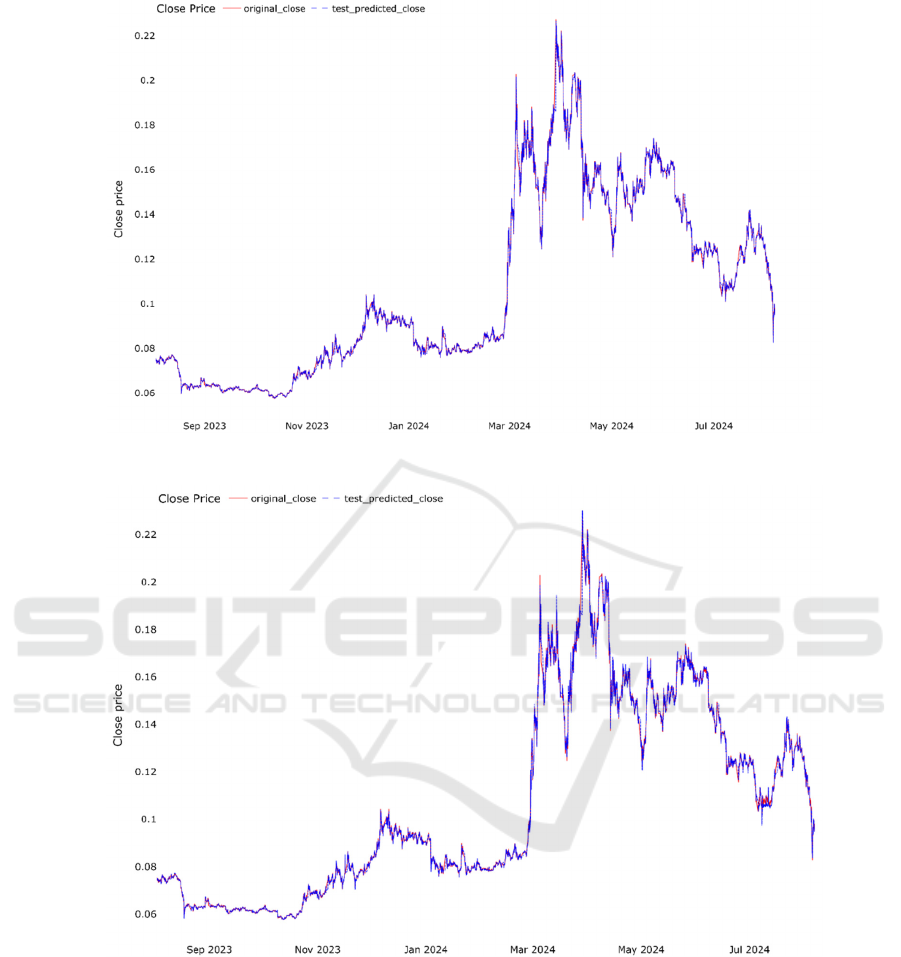
Figure 2: Prediction results of linear regression model (Photo/Picture credit: Original).

Figure 3: Prediction results of random forest model (Photo/Picture credit: Original).

3.2 Model Performance

The Figure. 2 shows the prediction results of the

linear regression model. The MAE value of the model

is 0.0009766767, the MSE value is 0.0000035667,

and the R-squared value is 0.9988252299. Figure. 3

shows the prediction results of random forest model.

The MAE value is 0.0011575186, the MSE value is

0.0000040188, and the R-squared value is

0.9986762996. Figure. 4 depicts the prediction results

of LSTM model. The MAE value of the model is

0.0009608147, the MSE value is 0.0000035197, and

the R-squared value is 0.9989077614. Figure. 5

presents the prediction results of Transformer model.

The MAE value of the model is 0.0027048813, the

MSE value is 0.0000180260, and the R-squared value

is 0.9940644514. Table 1 summarizes the test results

of the trained linear regression model and random

forest model. The indicators of the test model are

MAE, MSE, R

Prediction of DOGE Based on Random Forest, Long Short-Term Memory and Transformer

191

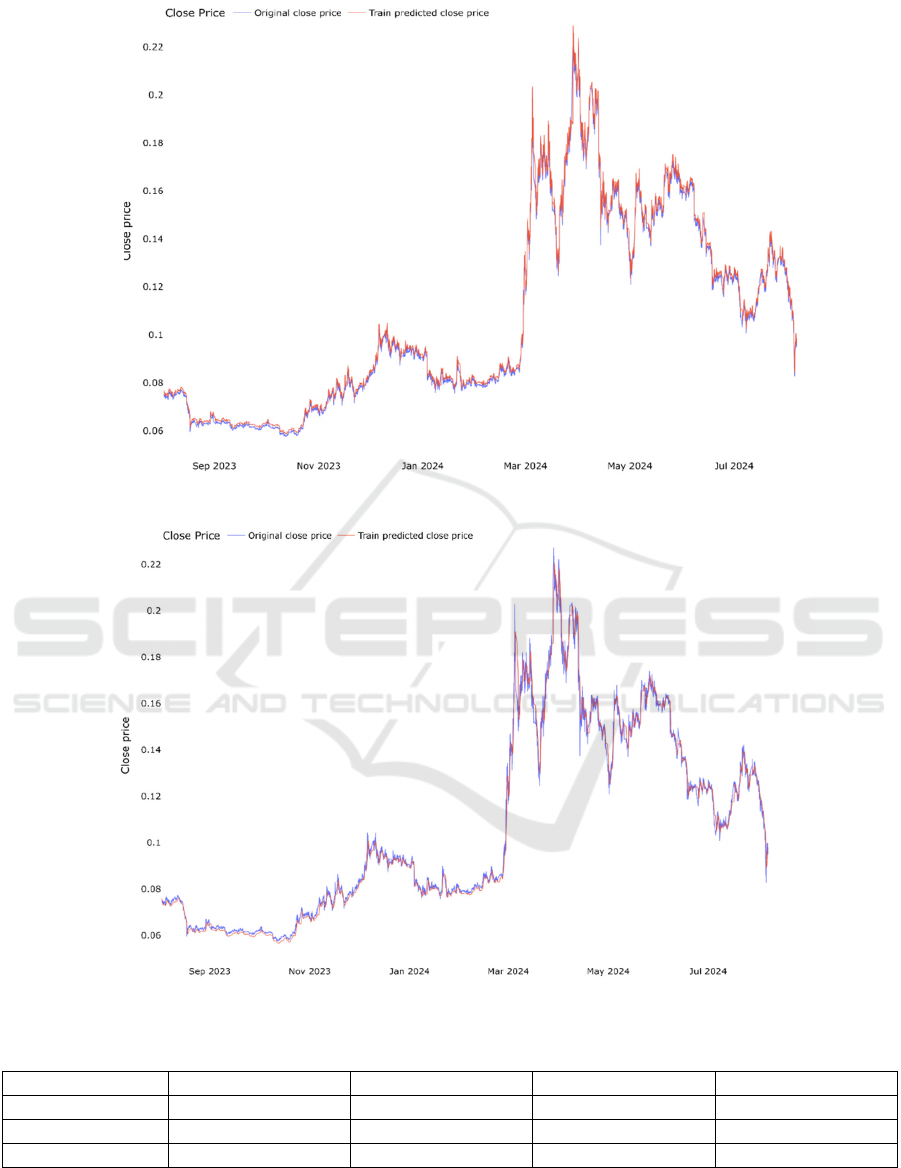
Figure 4: Prediction results of LSTM model (Photo/Picture credit: Original).

Figure 5: Prediction results of Transformer model (Photo/Picture credit: Original).

Table 1: The test results of the models.

Linear re

ression Random fores

LSTM Transforme

MAE 0.0009766767 0.0011575186 0.0009608147 0.0027048813

MSE 0.0000035667 0.0000040188 0.0000035197 0.0000180260

0.9988252299 0.9986762996 0.9989077614 0.9940644514

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

192

3.3 Explanation and Implications

Table 1 summarizes the performance of the four

models concerning for the Dogecoin 1-hour interval

price. As shown, The LSTM model performed the

best with an MSE of only 0.0000035197, followed

closely by the linear regression model

(0.0000035667). The random forest model is worse in

terms of mean squared error performance

(0.0000040188), while the Transformer model

performs the worst, with an MSE value of

0.0000180260. The result shows that the LSTM

model is particularly good at capturing temporal

dependencies in sequential data., which is crucial for

time series prediction tasks. The LSTM model was

designed to remember long-term dependencies while

efficiently ignoring irrelevant information, making

them well-suited for predicting short-term trends and

fluctuations in DOGE prices.

LSTM has several advantages over linear

regression and random forest in terms of time series

forecasting. First and foremost, Time series data

including both short- and long-term dependencies

may be precisely captured using LSTM for it has the

ability to store data from earlier time steps and utilize

it to make predictions in the future. In contrast, linear

regression only captures linear relationships between

variables and cannot handle complex temporal

dependencies. Random forest, while capable of

handling nonlinear relationships, is based on decision

trees and is not inherently designed to process

sequential data with time dependencies. Meanwhile,

LSTM can naturally handle nonlinear relationships in

time series. Last but not least, the unique feature of

LSTM is its built-in memory units and forget gates,

which can selectively remember or forget information,

effectively filtering out noise and retaining useful

information. This mechanism allows LSTM to excel

in handling long sequences. Linear Regression and

Random Forest do not have this memory and

selective forgetting mechanism, so their ability to

capture patterns in long time series data is limited.

The transformer model, however, while highly

effective in tasks like natural language processing,

may not be as naturally suited to the time series

prediction task here. Transformers rely on self-

attention mechanisms, which, although excellent at

handling long-range dependencies, may struggle with

capturing the short-term dynamics typical in time

series data. Moreover, the dataset of Dogecoin is

relatively small, the Transformer model can’t learn

the patterns in the time series effectively, leading to

poorer performance.

This experiment explored the accuracy of four

models in predicting the price of Dogecoin and found

a better way to predict the price of Dogecoin. To go

further, some new laws or patterns discovered in the

experiment can become the basis for future research

on time series problems or provide new research

directions for such tasks. At the same time, for

investors, this experiment can help them better

understand the virtual currency represented by

Dogecoin and make profits from investment. Thus,

they can better understand market behavior and

market rules in complex changes, and then explore

how to use predictive models for investing and risk

aversion.

3.4 Limitations and Prospects

This study still has certain limitations. In terms of

data, the hourly price frequency of Dogecoin is too

low, and the price every 5 seconds may help the

model predict more accurately. At the same time, the

number of features of Dogecoin is too small, and

higher-dimensional data can be further collected. In

terms of models, due to limitations of experimental

conditions, the author cannot explore all models, but

there are indeed many valuable models that can be

explored in terms of price prediction of Dogecoin. To

improve this research, the author intends to examine

more methods, such as CNN or the Diffusion model.

At the same time, the author plans to collect more

frequent and more dimensional price data for further

research.

4 CONCLUSIONS

To sum up, this study investigates machine learning

techniques based on sample characteristics of

samples and dimensions to predict Dogecoin prices.

This paper compares the performance of four models,

i.e., Linear Regression, Random Forest, LSTM, and

Transformer, in predicting Dogecoin prices, and finds

that the LSTM model delivers the best results. The

results show that the LSTM model performs much

better than the others because of its robustness in

handling nonlinear interactions and capturing

temporal dependencies. Linear Regression and

Random Forest models underperformed in dealing

with complex time series data, while the Transformer

model also did not meet expectations in this task. The

limitation of this article is that the data volume and

feature dimensions of the sample are small, which

affects the prediction effect of the model. Future

research could focus on optimizing hyperparameters

Prediction of DOGE Based on Random Forest, Long Short-Term Memory and Transformer

193

and exploring larger datasets or more sophisticated

feature engineering methods. The importance of this

research lies in providing a valuable model

comparison for cryptocurrency price prediction in

financial markets, especially highlighting the

potential of the LSTM model in such tasks.

REFERENCES

Aravindan, J., Sankara, R. K. V., 2022. Parent Coin based

Cryptocurrency Price Prediction using Regression

Techniques. In 2022 IEEE Region 10 Symposium

TENSYMP pp. 1-6.

Chohan, U. W., 2021. A history of Dogecoin. Discussion

Series: Notes on the 21st Century, 11.

Dhande, A., Dhani, S., Parnami, S., Vijayakumar, K. P.,

2024, Cryptocurrency Price Prediction Using Linear

Regression and Long Short-Term Memory LSTM.

Academia, 12.

Dogecoin, 2024: Retrieved from https://dogecoin.com/

Nani, A., 2022. The doge worth 88 billion dollars: A case

study of Dogecoin. Convergence, 286, 1719-1736.

Singla, M., Gill, K. S., Chauhan, R., Pokhariya, H. S.,

Lande, J., 2024. Dogecoin price prediction–Through

Utilization of XGBoost Model GridSearchCV

Classification Technique. In 2024 IEEE 9th

International Conference for Convergence in

Technology I2CT pp. 1-6.

Sridhar, S., Sanagavarapu, S., 2021. Multi-head self-

attention transformer for dogecoin price prediction. In

2021 14th International Conference on Human System

Interaction HSI pp. 1-6.

Srivastava, V., Dwivedi, V. K., Singh, A. K., 2023.

Cryptocurrency price prediction using enhanced PSO

with extreme gradient boosting algorithm. Cybernetics

and Information Technologies, 232, 170-187.

Wallbridge, J., 2020. Transformers for limit order books.

arXiv preprint arXiv:2003.00130.

Zhang, S., Mani, G., 2021. Popular cryptoassets Bitcoin,

Ethereum, and Dogecoin, Gold, and their relationships:

Volatility and correlation modeling. Data Science and

Management, 4, 30-39.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

194