Prediction of Bitcoin Daily Returns Based on OLS, XGBoost,

and CNN Machine Learning Models

Ye He

Faculty of Business and Economics, The University of Hong Kong, Hong Kong, China

Keywords: Bitcoin, Machine Learning, Ordinary Least Squares (OLS), XGBoost (Extreme Gradient Boosting),

Convolutional Neural Network (CNN).

Abstract: This study seeks to predict Bitcoin's daily return through a comparison of three machine learning models:

Ordinary Least Squares (OLS), XGBoost (Extreme Gradient Boosting), and Convolutional Neural Network

(CNN). To assess the effectiveness of these models in capturing Bitcoin market fluctuations, the relevant

market data is first cleaned and standardized, followed by training and testing with the three models. The

findings reveal that the OLS model excels in stable market conditions, exhibiting a smaller prediction error.

Meanwhile, the XGBoost model shows promise in handling nonlinear relationships and market fluctuations,

albeit with a larger prediction error. Unfortunately, the CNN model did not meet expectations, struggling to

effectively capture the market's complex characteristics. According to the analysis, this research highlights

that various machine learning models demonstrate differing applicability for predicting Bitcoin returns across

diverse market environments. Future studies could enhance prediction accuracy by optimizing model

parameters and incorporating additional feature variables.

1 INTRODUCTION

Bitcoin first emerged in 2009 as a digital asset

constructed on the concept of blockchain which is the

inception of the decentralised economy (Mulligan et

al., 2020). By employing a decentralized distributed

ledger and complex encryption algorithms it

guarantees the openness, safety and non-alterability

of the transactions (Benos et al., 2019). Following the

emergence of Bitcoin, blockchain technology has

been gradually introduced into several various

industries of service industry including financial

services, supply chain industry, smart contracts and

so on which has greatly driven the progress of

blockchain technology (Hughes et al., 2019).

However, with the development of Bitcoin. Its huge

energy consumption problem has become one of the

main concerns, the computational process in the

mining of the Bitcoin consumes a lot of energy, and

this leads to high energy consumption issues (Gad et

al., 2022). Furthermore, the problem of forks is also

haunting Bitcoin, which mainly arises due to the

discord in the community regarding formation of new

chains and market fluctuations (Kumari et al., 2023).

These technical and market uncertainties have

exacerbated the market risks of Bitcoin, especially in

the absence of a clear regulatory framework (Tripathi

et al., 2023).

In the last few years with the emergence of

Bitcoin and other cryptocurrencies the prediction of

their price movements has become an important area

of interest in both academia and financial markets.

Previous research employed conventional

econometric models including time series, and linear

regression models to forecast the Bitcoin prices,

however, because of the high fluctuation and non-

linearity of the Bitcoin market, these conventional

techniques provide less accurate prediction (Chen,

2023). For this purpose, the growing number of

studies has adopted machine learning process to

predict the Bitcoin price because these models can

learn the complex patterns and non-linearity in the

market (Ho et al., 2021). For instance, the models

employed include support vector machines (SVM),

random forests as well as the long short-term memory

networks (LSTM); and these models yield high

accuracy in the context of Bitcoin price prediction

(Ampountolas, 2023). Besides, some studies have

also used enhanced models like Gated Recurrent

Units (GRU) and Deep Neural Networks (DNN) for

enhancing the Bitcoin price prediction system (Seabe

et al., 2023). These models hold the following

He, Y.

Prediction of Bitcoin Daily Returns Based on OLS, XGBoost, and CNN Machine Learning Models.

DOI: 10.5220/0013212400004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 181-187

ISBN: 978-989-758-726-9

181

advantages in capturing market changes by handling

features and complex relations between the features.

Despite advancement of machine learning models

in the Bitcoin price prediction, there are some

limitations and future research gaps in the study. For

instance, some studies have directly fed data into the

model without taking into consideration factors such

as data frequency, sample dimension and feature

selection which leads to overfitting of the model or

unstable prediction (Khedr et al., 2021). The

development of future research can enhance the data

preprocessing and feature engineering steps and can

investigate the way of enhancing the performance and

stability of the model under more frequent and

different sample data (Ji et al., 2019).

The motivation of this study arises from the fact

that the market of Bitcoin is highly unpredictable and

has a lot of uncertainties and the daily returns of

Bitcoin is a difficult task but it is very important due

to the fluctuating nature of the Bitcoin market. First,

the context of the Bitcoin market and the role of return

forecasting are discussed, and then the source and

features of the data set used, and finally the

theoretical foundation and concrete implementation

steps of the three models are explained and

introduced. Subsequently, through the process of

training and testing the models, the accuracy of the

models in estimating the returns of Bitcoin daily, the

error analysis and the strengths and weaknesses of the

models in the sense of capturing the market dynamics

are presented.

2 DATA AND METHOD

The data for this research is therefore obtained from

the investment platforms investing. com and Yahoo

Finance. The sample includes over 1,000 trading days

of Bitcoin. These data include the following main

variables: These are Date, Open, High, Low, Close,

Adjusted Close, Volume, and Return. Among them,

the return is the main dependent variable of this study.

First, this study started with data cleansing and after

deleting all the missing values, outliers for the sake of

data integrity and data consistency. All numerical

variables were normalized and this helps to avoid

problems associated with differing feature

magnitudes which in turn stabilizes the model

training. Likewise, this study also computed

correlation matrix to have more insight on the co-

relation among the different features.

This study employed three forms of regression

models in order to forecast the daily return of Bitcoin.

The three machine learning models are Ordinary

Least Squares (OLS), XGBoost (Extreme Gradient

Boosting), and Convolutional Neural Network

(CNN).

This research selected the Ordinary Least Squares

(OLS) model, which is the simplest linear model, as

the basic model for predicting the daily return of

Bitcoin. OLS model retains that there is a straight line

relationship between the target variable and the input

features and seeks for the best line that would bring

out the least mean squared error. This method of

linear regression is very useful for initial analysis of

the data for the presence of linear relations and serves

as a basis for subsequent more complex models. This

study separated the whole data set into training data

and testing data in the proportion of 7:3. This division

makes it possible for the model to learn on enough

data as well as make a proper performance evaluation

on the unseen data. In training phase, the weights are

updated iteratively to estimate a straight line which

minimizes the sum of squared errors between

predicted and actual value. Such a process helps the

model to learn the correlation between the input

features and the yields in Bitcoins.

XGBoost is based on the gradient boosting

decision trees and has high nonlinear modeling

abilities. While compared with simple linear models,

XGBoost can learn deeper and more complex

relationships between input features and target

variables, which will make XGBoost better than the

others when dealing with data contains nonlinear

features. In case of using the XGBoost model, it is

important to standardize the input features so that the

features are in the same units. To achieve better

results of the model, this study applied the grid search

and cross-validation to adjust the parameters of the

model. These hyperparameters include learning rate,

maximum tree depth and others which define the

capability of the model on prediction. Once optimized

the parameter tuning, then this paper proceeded to

train the XGBoost model using the training data set.

XGBoost constructs a series of decision trees and

with the new tree trying to minimize the prediction

error of the previous tree and hence, achieving

improvement in the efficiency of the model.

CNN is a machine learning model that is typically

employed for the processing of images, however for

this particular research, this study trained it on time

series data. CNN models enable the learner to learn

complex patterns and nonlinear relationships in the

data and therefore have an added advantage in

estimating Bitcoin’s daily return. First, in view of the

CNN model input format, this study enlarged the data

from two-dimensional format to three-dimensional

tensor. Subsequently, one developed a CNN model

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

182

with more than one convolutional, pooling and fully

connected layers. The convolutional layer performs

feature extraction of the data locally while the pooling

layer reduces the dimension of features and also

offers protection against overfitting of the data; full

connection layer establishes the connection between

the high dimensional features and the output layer to

produce the final prediction.

In order to assess the performance of each model

more comprehensively this study used the same

metrics to compare the OLS, XGBoost, and CNN

models on the test set. This was made possible by the

use of additional model evaluation metrics including

the R-squared (R²), mean absolute error (MAE), and

the mean squared error (MSE). The nearer the value

of R² to 1, the better the fitting of the model to the

data; the smaller the MAE, the smaller is the

prediction error of the model and the MSE is another

measure which is more sensitive to large errors.

3 RESULTS AND DISCUSSION

3.1 Correlation Analysis

In this study, for the purpose of determining the

feature variables with the highest correlation to

Bitcoin’s daily yield, this study ran a correlation

analysis on the data set and depicted it with the help

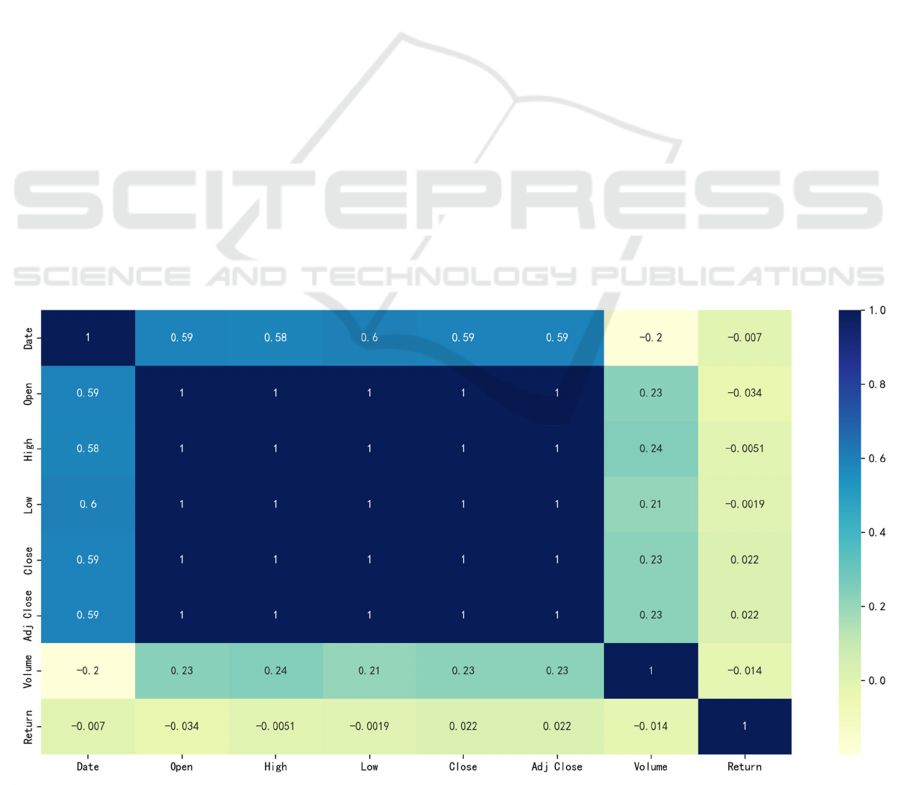
of a heat map (seen from Fig. 1).

From the heat map, the five price-related variables,

namely the Open, High, Low, Close and the Adj

Close, have almost perfect positive relationship and

the coefficient of correlation is also close to 1. Since

these variables are highly correlated, this has to

screen among them in a way to prevent

multicollinearity from affecting the model’s ability to

predict. In light of this, it decided to use only the

variables with the highest correlation to the yield

while excluding those which are redundant and might

add more noise to the model. In fact, return has a

much weaker relationship with each variable, with

correlation coefficients at -0.034 with opening price.

The correlation between 014 with Volume is 0.022

with adjusted closing price.

When choosing features, this study was concerned

with those that are most related to yield. However, it

is clear from the heat map that these variables are not

very much correlated with the yield; still, this

researcg chose Open, Volume, Close, and Adj Close

as the independent variables of the model. Despite the

fact that Open has a rather low coefficient of

dependence, it plays a significant role in prediction,

as it is the initial price of the market (as depicted in

Fig. 2). Volume shows the operation of the market

and has influence on yield in potential. Although

Close and Adj Close have a very low association with

yield, they still have some predictive value for the

change in yield, hence they are added into the model

equation.

Figure 1: Heat Map of Five Price-Related Variables (Photo/Picture credit: Original).

Prediction of Bitcoin Daily Returns Based on OLS, XGBoost, and CNN Machine Learning Models

183

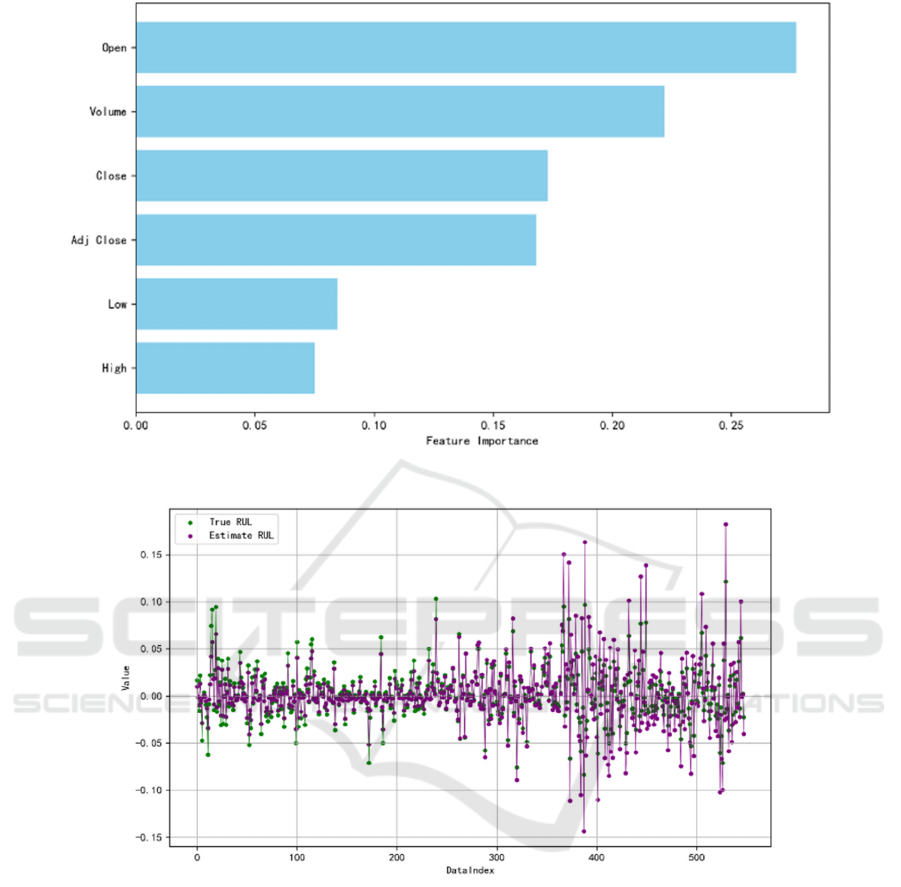
Figure 2: Feature Importance in Financial Model (Photo/Picture credit: Original).

Figure 3: OLS Model Performance (Photo/Picture credit: Original).

3.2 Performance of the Models

As shown in Fig. 3, the values predicted by the OLS

model are highly correlated to the actual values. First,

the coefficient of determination, R² is 0.7499, which

means that the accuracy of the model is about 75%

that is a high level in the financial time series

forecasting. This study also obtained the MSE and

MAE which is 0.000164 and 0.0076 respectively. The

value of MSE is low, which suggests that the total

error of the model is low in the forecast of daily

returns; while the value of MAE also shows that the

average error of the model is also small in the forecast

of daily returns. According to the evidence provided

in the graph, it is clear that the OLS model which is

relatively easy to use has great predictive power for

the trend of Bitcoin daily yield.

However, for periods of high turbulence in the

market, the prediction error is higher than has been in

other cases. This means that the OLS model might not

be so effective in the analysis of extremely nonlinear

or turbulent periods in history. For this reason, it is

important to incorporate other methods that might

help remedy the weaknesses of the OLS analysis,

hence the need to further consider XGBoost and CNN

models in this study.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

184

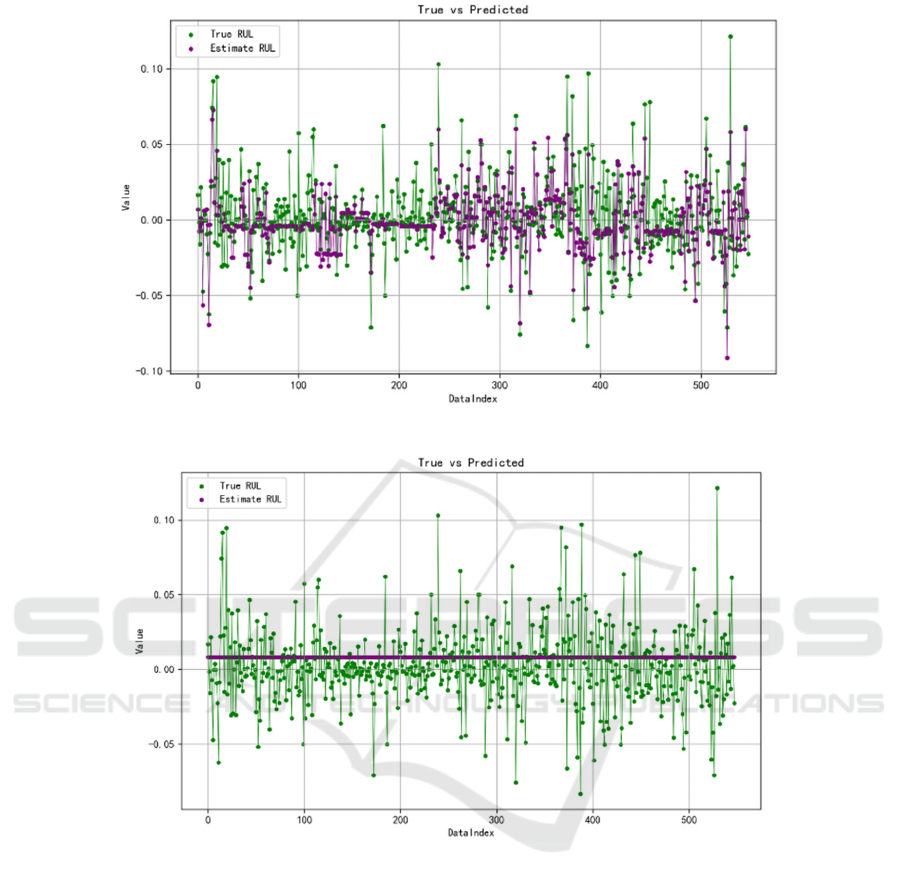
Figure 4: XGBoost Model Performance (Photo/Picture credit: Original).

Figure 5: CNN Model Performance (Photo/Picture credit: Original).

As shown in Fig. 4, the model records an R2 value

of 0.5291 meaning that it is possible to capture only

slightly more than half of the variations in the data by

employing XGBoost. Despite this R

value which

makes room for more complexities by XGBoost, the

explanatory power of the XGBoost model is

compromised against the OLS model. This could be

because in the time series of Bitcoin’s daily return

data, linear features are quite powerful and ordinary

structures do not work for such data but XGBoost

excels in nonlinearities. Thus, regarding this portion,

there remains little scope in using XGBoost to

improve upon the performance level of OLS. In

addition, the MSE of the XGBoost model is 0.00031,

which is significantly higher than the 0.000164 of the

OLS model, indicating that the overall prediction

error of the model is large. The MAE is 0.0123, which

is also higher than the 0.0076 of the OLS model,

further confirming that XGBoost is not as stable as

OLS on the current dataset.

Therefore, it can be stated that while using the

XGBoost model one can solve complex patterns to a

certain extent; however, its performance in terms of

predicting Bitcoin’s daily yield is lower than the OLS

model. This may mean that while XGBoost has an

edge of capturing intricate non-linear patterns, some

of these non-linear features are not very important in

today’s data set, or that because of the model’s

complexity, it over trains during the training phase

and thus has poor performance in the test data.

Prediction of Bitcoin Daily Returns Based on OLS, XGBoost, and CNN Machine Learning Models

185

In theory, CNN works quite well in capturing

patterns; however, its performance in the present

study is not very impressive as clearly deduced from

Fig. 5. To be specific, the coefficient of determination

(R²) of the CNN model is -0.0369, which is dwarfed

by the OLS and XGBoost models, most likely

because the model has been able to capture very little

useful information. What this demonstrates is that the

OLS outperforms R² of these models where R²

approaches the range of zero or thereabouts are rare.

This shows the limitation of this CNN in such,

Keywords: R², degeneracy, prediction accuracy,

convolution neural networks.

In addition, it should be mentioned that the

performance of the CNN model is disappointing

when measured by MSE or MAE metrics. The MSE

was recorded at 0.000682, almost four times the

shagger OLS model, which implied an even larger

difference between the predicted and the actual

outcome. The MAE is 0.0179, which as well fixed the

high value and cannot be related to OLS models and

XGBoost models. Such high error indicators imply

that the CNN model is not very reliable in making

predictions of Bitcoin per day yield and predictions

made have fairly conspicuous bias.

In light of these results, it can be inferred that the

CNN model could be deficient for many reasons. First,

even though CNN is well-established and enjoyed

great advances in image processing, its convolution

operation may not be sufficient for forecasting, and

capturing the complex dependencies of time-series

financial data. More particularly, with regards to

financial assets like Bitcoin which tend to be very

volatile as well as nonlinear in nature, learning useful

patterns from sparse training data can be a daunting

task for CNN. Second, the model design and

parameterization of the CNN may also be prohibitive.

3.3 Discussion and Recommendations

The OLS model is satisfactory, evidenced by R² value

of 0.7499 meaning the model is capable of explaining

around 75% of the variability of such data.

Additionally, both MSE and MAE's mean square

error recording low figures of 0.000164 and 0.0076

respectively. This preliminary finding serves to

confirm that the daily return on Bitcoin can be

modelled with a certain degree of stability linearity

which the OLS can model more correctly when it is

not in a volatile market.

However, in complex and volatile environments,

additional knowledge is rendered from the XGBoost

model. It indicates that the R-squared measure

(0.52891) among considered XGBoost approaches is

not especially impressive, although it does indicate

some potential in a nonlinear modeling context. Due

to the ensemble approach employed by XGBoost,

various decision trees that the algorithm contains,

XGBoost is more adaptive to abrupt changes in the

market. Despite the fact that XGBoost has an MSE of

0.00031 and a MAE of 0.0123, both higher than the

OLS model, such errors seem to be typical for such

types of models, 'XGBoost' may be useful in targeting

reversals and abnormal returns.

On the other hand, the accuracy of the CNN model

leaves much to be desired. The R-squared figure for

the CNN model can be calculated at -0.0369, where

all other external models that have OLS and XGBoost

have fared better, which means that CNN has almost

closed out on viable market data. Its MSE is 0.000682

and MAE is 0.0179, which are not promising results

compared with any reasonable prediction in this task.

From the insights provided through the above

discussion, this study obtained several key

investment suggestions. First, in a less favorable

market, passive investments using statistical linear

models based on OLS may be efficient and would

stabilize returns, which is quite useful for low-risk

individuals. Second, when volatile, an investor can

seek complex relations based on nonlinear models

such as XGBoost, though this has its limitations as

there are large prediction errors that come with such

models. However, while parts of deep learning

models like CNN are efficient in other areas like

image classification, in the treatment of daily yield of

Bitcoin, where there is financial time series data is

high volatility and complex, their merits do not shine

as they should, thus a combination with other

approaches focusing on reducing errors is required.

3.4 Limitations

However, this study has some shortcomings and

defetcs. First, the dataset do not include certain

phenomena for which many experts seek correlation

with the price of bitcoin, such as macroeconomic

variables or voting behavior of the market; secondly,

hyper-parameter tuning of XGBoost and CNN is also

not sufficiently addressed. This could be a limitation

on the maximum ability of these models; furthermore,

this study has not examined the use of combined

models and their predictive enhancement. Future

studies in this area may be directed to the broadening

intensity of the data set scope, further focusing on the

model parameters, employing less rigid data layer

segmentation strategies, and assessing the potential of

hybrid models in enhancing the prediction effect.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

186

4 CONCLUSIONS

To sum up, this paper aims to investigate the

predictive capacity of OLS, XGBoost, and CNN

decision-making models on the daily return of Bitcoin

and study the performance of various models with

time series of financial data. The findings state that

the econometric OLS model is reliable under low

market volatility and offers reasonable level

inaccuracies of predictions; the XGBoost model

possesses high potential in nonlinear and even

cyclical relationships and variations of the market,

although its inaccuracies are high always; and state

the goal of the CNN model for this study was

overstated as it was unable to appropriately track the

diverse movements of bitcoin price ranges. The

shortcomings of this paper include the scope of the

data set, the lack of thorough consideration of

macroeconomic factors to examine their effects on

the bitcoin prices and the model parameters tuning

that could have been enhanced. It would also be

necessary to advance the level of parameter masking

and look for more accurate models that can withstand

the ups and downs of the price.

REFERENCES

Ampountolas, A., 2023. Comparative Analysis of Machine

Learning, Hybrid, and Deep Learning Forecasting

Models: Evidence from European Financial Markets

and Bitcoins. Forecasting, 52, 472–486.

Benos, E., Garratt, R., Gurrola-Perez, P., 2019. The

Economics of Distributed Ledger Technology for

Securities Settlement. Ledger, 4.

Chen, J., 2023. Analysis of Bitcoin Price Prediction Using

Machine Learning. Journal of Risk and Financial

Management, 161, 51.

Dutta, A., Kumar, S., Basu, M., 2020. A Gated Recurrent

Unit Approach to Bitcoin Price Prediction. Journal of

Risk and Financial Management, 132, 23.

Gad, A. G., Mosa, D. T., Abualigah, L., Abohany, A. A.,

2022. Emerging Trends in Blockchain Technology and

Applications: A Review and Outlook. Journal of King

Saud University - Computer and Information Sciences,

349, 6719–6742.

Ho, A., Vatambeti, R., Ravichandran, S. K., 2021. Bitcoin

Price Prediction Using Machine Learning and

Artificial Neural Network Model. Indian Journal of

Science and Technology, 1427, 2300–2308.

Hughes, A., Park, A., Kietzmann, J., Archer-Brown, C.,

2019. Beyond Bitcoin: What blockchain and distributed

ledger technologies mean for firms. Business Horizons,

623, 273–281.

Ji, S., Kim, J., Im, H., 2019. A Comparative Study of Bitcoin

Price Prediction Using Deep Learning. Mathematics,

710, 898.

Khedr, A. M., Arif, I., P V, P. R., El-Bannany, M.,

Alhashmi, S. M., Sreedharan, M., 2021.

Cryptocurrency price prediction using traditional

statistical and machine

‐

learning techniques: A

survey. Intelligent Systems in Accounting, Finance and

Management, 281, 3–34.

Kumari, V., Pradip Kumar Bala, Chakraborty, S., 2023. An

Empirical Study of User Adoption of Cryptocurrency

Using Blockchain Technology: Analysing Role of

Success Factors like Technology Awareness and

Financial Literacy. Journal of Theoretical and Applied

Electronic Commerce Research, 183, 1580–1600.

Mulligan, C., Godsiff, P., Brunelle, A., 2020. Boundary

Spanning in a Digital World: The Case of Blockchain.

Frontiers in Blockchain, 3.

Seabe, P. L., Moutsinga, C. R. B., Pindza, E., 2023.

Forecasting Cryptocurrency Prices Using LSTM,

GRU, and Bi-Directional LSTM: A Deep Learning

Approach. Fractal and Fractional, 72, 203.

Tripathi, G., Ahad, M. A., Casalino, G., 2023. A

Comprehensive Review of Blockchain technology:

Underlying Principles and Historical Background with

Future Challenges. Decision Analytics Journal, 91,

100344.

Prediction of Bitcoin Daily Returns Based on OLS, XGBoost, and CNN Machine Learning Models

187