Novel Portfolio Construction Based on Stocks, Traditional Stock

Indices, Futures and Cryptocurrencies

Chang Su

Department of Commerce, Macau University of Science and Technology, Macau, China

Keywords: Mean-Variance Model, Maximum the Sharpe Ratio, Minimum the Risk.

Abstract: As emerging assets continue to develop, they are increasingly integrated into traditional portfolio construction.

Given that these new asset classes often exhibit low correlation with traditional assets, their inclusion can

enhance overall portfolio performance. This study, based on Markowitz's mean-variance theory, utilizes five

years of historical data to construct a portfolio consisting of six assets, including stocks, traditional stock

indices, futures, and cryptocurrencies. Two objective functions are applied: maximum the Sharpee ratio and

minimum variance. According to the analysis, the results demonstrate that the portfolio optimized for the

maximum Sharpee ratio achieves the highest returns, while the portfolio optimized for minimum variance

shows better stability. By comparing asset weights and cumulative net value chart, the effectiveness of these

objective functions in portfolio optimization is validated. This research contributes to the literature by

illustrating how Modern Portfolio Theory (MPT) can be used to combine traditional and new asset classes to

meet diverse investment objectives.

1 INTRODUCTION

Since its introduction in the mid-20th century,

portfolio theory has undergone significant

development. In 1952, Harry Markowitz introduced

the mean-variance optimization framework, which

laid the foundation for modern portfolio theory

(Markowitz, 1952). Markowitz’s theory emphasized

reducing risk and optimizing returns through the

construction of diversified portfolios with assets that

are not perfectly correlated.

Following Markowitz, William Sharpee's Capital

Asset Pricing Model (CAPM), proposed in 1964,

extended this theory by introducing the concept of the

Security Market Line, which establishes the

relationship between risk and expected return,

assisting investors in evaluating asset performance

under market equilibrium (Sharpee, 1964). Eugene

Fama's Efficient Market Hypothesis (EMH),

proposed in 1970, challenged the traditional

assumptions of market rationality and impacted

portfolio management (Fama, 1970). Behavioral

finance and risk factor models further enriched

portfolio theory. Others’ prospect theory revealed

common irrational behaviors in investor decision-

making (Kahneman & Tversky's, 1979), while Fama

and French's three-factor and five-factor models

advanced the understanding of risk premiums and

returns (Fama & French, 1993).

With technological advancements, the integration

of big data and machine learning has provided new

tools for portfolio optimization. Others found that

deep learning and reinforcement learning algorithms

can enhance the accuracy and efficiency of

investment decisions (He & Liao, 2021). Additionally,

the rise of high-return cryptocurrencies offers new

perspectives for portfolio development (Chen & Liu,

2022). In recent years, research on portfolio

construction has increasingly incorporated emerging

asset classes and advanced technologies to improve

traditional optimization methods.

When integrating futures into traditional

portfolios, scholars analysed the role of commodity

futures (Gorton & Rouwenhorst, 2021). Their study

indicates that commodity futures, due to their low

correlation with traditional assets, can effectively

hedge against inflation and market volatility (Gorton

& Rouwenhorst, 2021). Similarly, Szymanowski

(2021) explored the role of commodities in portfolios,

finding that they offer distinct risk-return

characteristics compared to traditional financial

assets, thereby enhancing overall portfolio

performance (Szymanowski, 2021).

Cryptocurrencies, as a new asset class, are

Su, C.

Novel Portfolio Construction Based on Stocks, Traditional Stock Indices, Futures and Cryptocurrencies.

DOI: 10.5220/0013208700004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 175-180

ISBN: 978-989-758-726-9

175

increasingly being added to traditional portfolios.

Some researchers discovered that cryptocurrencies,

with their low correlation and high return potential,

effectively diversify traditional portfolio risks and

improve risk-adjusted returns (Chen & Liu, 2022).

Some advanced technologies also promote the

development of portfolio research. The introduction

of machine learning techniques has provided new

methods for portfolio optimization. He and Liao

explored the application of deep learning and

reinforcement learning in portfolio management,

showing that these algorithms can identify market

patterns, refine investment strategies, and enhance

prediction accuracy (He & Liao, 2021). The role of

big data analysis has also been widely studied. Guo

and Lin found that sentiment analysis and market data

can enhance market trend forecasting and improve

risk management (Guo & Lin, 2022). Blockchain

technology further improves transparency and

efficiency in portfolio management. Zhang and Liu

noted that blockchain technology, through smart

contracts, automates transactions, reduces

intermediary costs, and enhances data security

(Zhang & Liu, 2023). Additionally, ESG

(Environmental, Social, and Governance) factors

have become a significant aspect of portfolio

management. Sullivan and Mackenzie found that

incorporating ESG standards not only improves

social responsibility performance but also generates

long-term financial returns (Sullivan & Mackenzie,

2021). These studies emphasize that integrating

emerging assets and technologies provides new

perspectives and tools for portfolio construction.

Although traditional portfolio theory offers

effective risk management tools, it encounters

limitations when dealing with emerging assets such

as cryptocurrencies. Introducing cryptocurrencies

into the portfolio provides new development

opportunities. The low correlation and high return of

cryptocurrencies compared to traditional stock

indices and futures give them unique value in asset

allocation. This study selects six assets and uses five

years of data to construct the portfolio based on

Markowitz's mean-variance theory, applying two

objective functions: maximizing the Sharpee ratio

and minimizing variance. Subsequently, by

comparing the asset weights and cumulative net value

charts of portfolios optimized with these two

objective functions, it is found that the portfolio

optimized for maximizing the Sharpee ratio achieves

the highest returns, while the minimum variance

portfolio maintains better stability, thus validating the

effectiveness of the model.

2 DATA AND METHOD

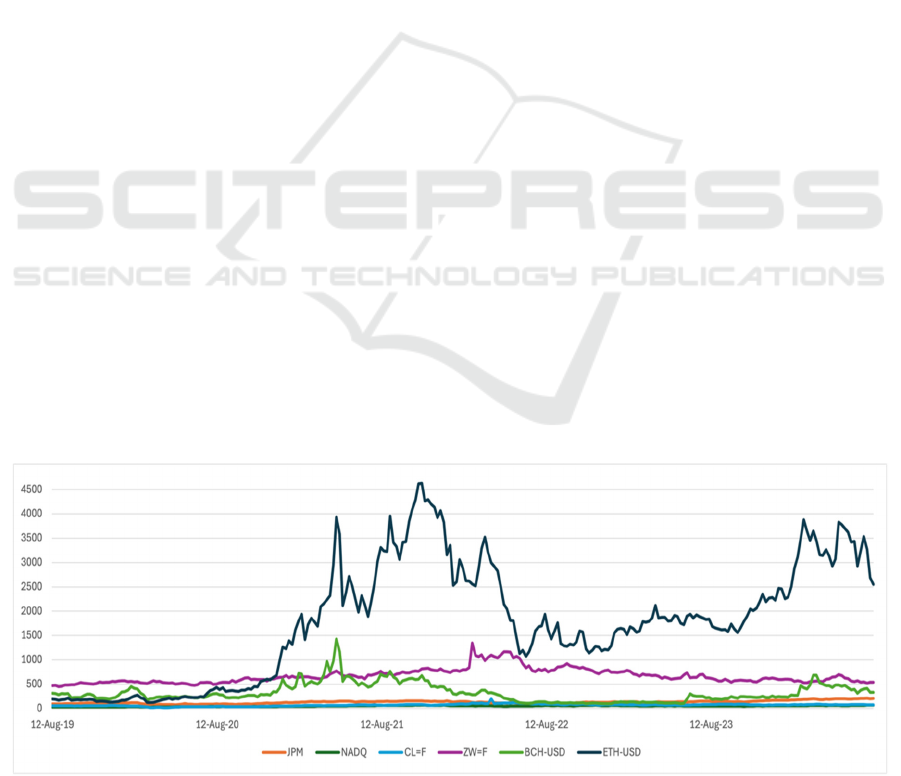
The data for six assets of the portfolio in the paper

comes from Yahoo Finance (Yahoo Finance, n.d.). As

shown in Figure. 1, these assets are JPMorgan Chase

& Co., NASDAQ, Crude Oil Futures, Wheat Futures,

Bitcoin Cash to US Dollar and Ethereum to US Dollar.

To ensure the validity of the portfolio, this paper uses

weekly data for five years from August 2019 to

August 2024. The six asset types selected are stocks,

traditional stock indices, futures and cryptocurrencies.

As a financial instrument, stocks are an indispensable

part of every portfolio. The traditional stock index has

low volatility, which provides the basic risk

protection for this portfolio. In addition, commodity

futures often move differently from stock prices,

which can hedge portfolio risk. Cryptocurrencies as a

new asset can add overall returns to the portfolio with

their high risk and high returns. Therefore, these four

different types of assets were chosen.

Figure 1: price change curves for six assets (Photo/Picture credit: Original).

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

176

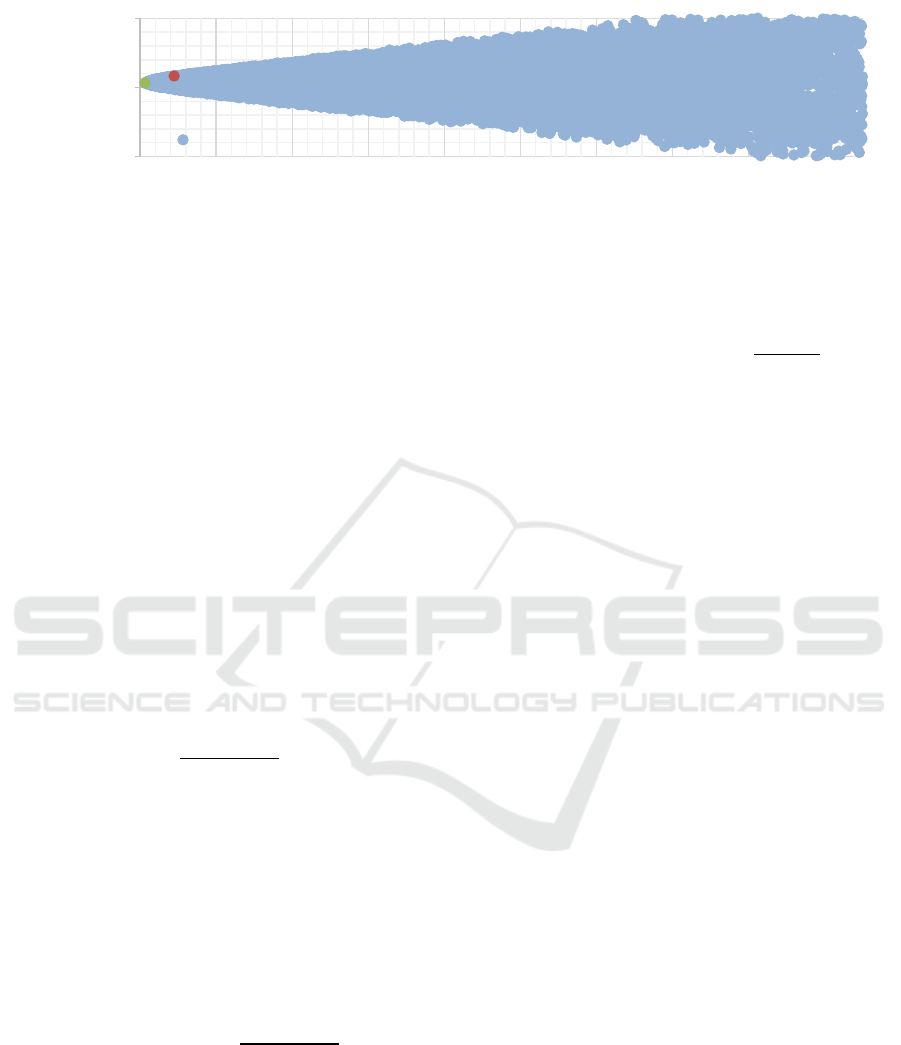
Figure 2: Efficient frontier retrieved by Excel (Photo/Picture credit: Original).

This paper use Excel to construct the portfolio.

Mean-variance model proposed by Markowitz is the

basis of portfolio construction in this paper. The

mean-variance model indicates that investors define

the standard deviation as the risk of the portfolio, and

the expected return is defined as the return of the

portfolio. This theory helps investors maximize

returns or minimize risks under different portfolio

risks. Based on the hypothesis that investors are

rational economic people, investors will adjust their

portfolios according to the behavior of the mean-

variance. When the expected return rate is the same,

the low-risk portfolio will be chosen. Additionally,

when the risks are the same, they will choose the high

return portfolio. According to Mean-variance model,

Using the Eq. (1) to achieve theExpected return of

portfolio:

𝑅



= 𝑊



∗𝜇 (1)

Here, 𝑅



is expected return of portfolio return, and 𝑊

is the weight of the selected asset. 𝜇 is expected

return of selected asset. Eq. (2) is used to calculate the

risk of the portfolio return:

𝜎



√

𝑊



∗𝛴∗𝑊 (2)

where 𝜎



is the standard deviation of the portfolio and

𝛴 is the covariance matrix of selected asset return

This paper utilizes two objective functions to

optimize the portfolio return and illustrates in the

Figure. 2. The first objective is to minimize the

standard deviation of portfolio. This approach focuses

on reducing portfolio risk by minimizing standard

deviation. Investors are risk averse, therefore

undoubtfully they choose the portfolio with lower risk

under the same expected return. The Eq. (3) of this

objective function is shown as:

𝑚𝑖𝑛𝜎



= 𝑚𝑖𝑛

√

𝑊



∗𝛴∗𝑊 (3)

It is limited by the following constraints.

∑

𝜔







=1 (4)

𝜔



≥ 0 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑖 (5)

The second objective is to maximum the Sharpee

ratio of the portfolio. The Sharpe ratio is used to

measure the excess return of each unit of risk. A

higher Sharpe ratio means that the investment

portfolio can obtain higher excess returns after taking

certain risks. Thus, investors can use the Sharpee ratio

to select the portfolio that receives the highest excess

return for the same level of risk. The objective

function is illustrated following:

𝑀𝑎𝑥 𝑆ℎ𝑎𝑟𝑝𝑒 𝑟𝑎𝑡𝑖𝑜 = 𝑀𝑎𝑥

(



)







(6)

Here, 𝐸𝑅



 is the expected return of portfolio, 𝑅



the risk-free interest rate, 𝜎



is the standard deviation

of the portfolio.

3 RESULTS AND DISCUSSION

3.1 Effective Frontier

The paper is based on these six assets using Excel to

simulate 50000 times of portfolio with different

weights. As illustrated in the Figure. 2, the shadow

formed by the blue scatter is the feasible set of this

portfolio. The upper boundary of the feasible set is the

efficient frontier. Under the certain risk, the points on

the efficient frontier are the portfolios that bring the

highest returns to investors, so these portfolios can

attract more investors to invest. The investment

portfolio studies in this paper are the minimum risk

portfolio and the maximum Sharpe ratio portfolio.

Both are portfolios that ultimately achieve the best

returns through asset allocation.

3.2 Model Performance

In the maximum Sharpe ratio portfolio (as shown in

Table 1), Ethereum has the largest weight, which is

41.24%. The asset with the smallest weight is Bitcoin

Cash at -10.58%, which indicates that Bitcoin Cash is

short. Maximizing the Sharpe ratio indicates the

highest excess return per unit risk. This portfolio buys

and holds the most Ethereum, illustrating that

investors are optimistic about the development

prospects of cryptocurrencies. In this portfolio,

cryptocurrencies can bring high return (Corbet et al.,

2018). Ethereum is a more flexible decentralized

application app. Compared with the digital currency

-0,05

0,05

0,025 0,075 0,125 0,175 0,225 0,275 0,325 0,375 0,425 0,475

Portfolio return

Portfolio risk

Efficient frontier

Novel Portfolio Construction Based on Stocks, Traditional Stock Indices, Futures and Cryptocurrencies

177

Bitcoin, it has a wider range of uses, such as providing

infrastructure for decentralized finance, non-fungible

tokens, and other blockchain application (VanEck,

n.d.). Therefore, Ethereum is more innovative and has

great room for development, which bring more return

to the portfolio. Shorting Bitcoin is to hedge the risks

of the cryptocurrency market. When the price of

Ethereum falls, part of the loss will be offset by

shorting Bitcoin Cash, thereby reducing the volatility

of the portfolio.

In the minimum risk portfolio, the Nasdaq index

has the largest weight, 48.05%, and Ethereum has the

smallest weight, -2.52%, indicating shorting

Ethereum. Since the portfolio seeks to minimize the

risk of the portfolio, the largest asset weight is placed

on the Nasdaq index. The index represents many

technology stocks that have strong profitability and

low volatility. Shorting high-yield and high-risk

Ethereum helps reduce the volatility of the entire

portfolio.

Comparing the two portfolios, JPMorgan Chase is

a large financial institution, which leads to more

stable stocks, so it accounts for a small proportion in

the maximum Sharpe ratio portfolio, and the risk is

higher in the portfolio that pursues the lowest risk, but

the difference in the proportion of JPMorgan Chase

in the two portfolios is not large, indicating that

JPMorgan Chase can play a stable market

performance in both asset portfolios. Crude oil

futures and wheat futures are commodities with high

volatility and are affected by various economic

factors such as exchange rates and supply and

demand. Therefore, the proportion of futures in the

two portfolios is quite different. The maximum

Sharpe ratio portfolio uses two futures to increase the

return of the portfolio, while another portfolio uses

less asset weight allocation to reduce risk.

Table 1: Asset weights of selected portfolio.

Weights

Maximum

Sharpe ratio

Minimum risk

JPM 0.2171687 0.257923747

NADQ 0.2632056 0.48055297

CL=F 0.1022184 0.029643431

ZW=F 0.1108830 0.029643431

BCH_USD -0.1058841 0.010999937

ETH_USD 0.4124083 -0.025222376

Table 2: Performance of two selected portfolio.

Portfolio risk

Portfolio

return

Sharpe

ratio

Maximum

Shar

e ratio

0.047 0.008 0.163

Minimum ris

0.028 0.003 0.097

As shown in Table 2, the portfolio risk, portfolio

return, and Sharpe ratio of the minimum risk portfolio

and the maximum Sharpe ratio portfolio are

calculated. As can be seen from the table, the

maximum Sharpe ratio portfolio has a higher return

and a higher risk. On the contrary, the minimum risk

portfolio has a lower return and a lower risk.

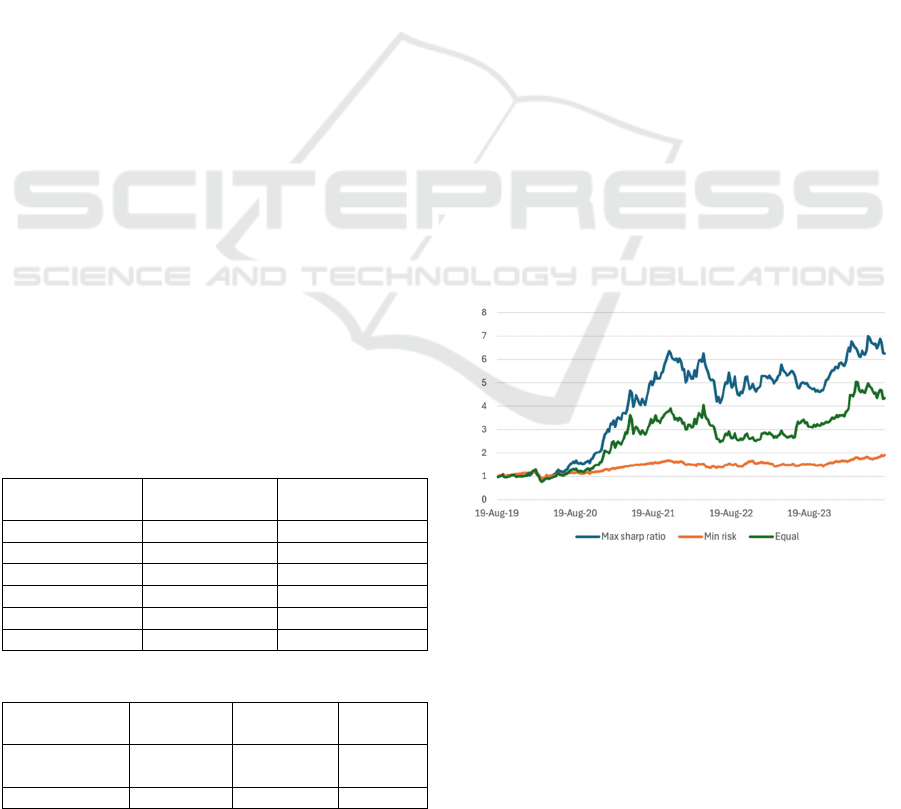
Figure. 3 is the cumulative net value chart of

portfolio, showing the performance of three different

investment portfolios from August 2019 to August

2024. The three investment portfolios are the

maximum Sharpe ratio portfolio, the minimum risk

portfolio and the equal asset weight portfolio. In

Figure. 3, the maximum Sharpe ratio portfolio has the

largest volatility in five years, but its growth rate is

also the highest, and the final cumulative net asset

value is 6.25. The cumulative net asset value of the

equal weight investment portfolio is less than that of

the maximum Sharpe ratio investment portfolio,

which is 4.35. Although the return performance of

this strategy is relatively good, this portfolio does not

have special measures to avoid market risks, which

means that if the market goes down or fluctuates

violently, the entire investment portfolio may suffer a

comprehensive loss. The minimum risk investment

portfolio has the lowest cumulative net asset value,

which is 1.90. All in all, this graph shows that the

maximum Sharpe ratio investment portfolio has the

best return, and the minimum risk investment

portfolio has a lower return, even lower than the equal

weight portfolio.

Figure 3: Cumulative net value chart of portfolio

(Photo/Picture credit: Original).

In summary, the investment portfolio constructed

by maximum Sharpe ratio selects assets with higher

returns to pursue a higher Sharpe ratio, even if it is

accompanied by greater market risks. Therefore, this

portfolio will perform better in a bull market and is

suitable for investors who pursue high returns and are

able to bear risks. The minimum risk investment

portfolio will perform better when the market

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

178

volatility is high, and the uncertainty is large.

Therefore, this portfolio is more suitable for risk-

averse investors, with lower investment risks and

stable returns.

3.3 Limitations and Prospects

The five-year data period used in this paper includes

the COVID-19 epidemic period. During this period,

there is a significant increase in the volatility of

different financial assets, and even anomalies such as

plummeting. The cryptocurrencies and futures in this

portfolio are less liquid, especially during times of

high market volatility or even liquidity depletion (Liu

& Tsyvinski, 2021). Therefore, extreme changes in

asset prices during an epidemic may affect the market

performance of the assets, while model results that

include this period may not be applicable to other

periods. The construction of portfolio in this paper is

based on the underlying mean-variance model, which

assumes that the expected returns of the assets follow

a normal distribution. However, new asset

cryptocurrencies are highly volatile in price, and the

distribution of returns does not always show a normal

distribution, but may be skewed and thick tailed, so

that a normal distribution tends to underestimate the

risks associated with extreme variations. (Klein et al.,

2018). Plus, the mean-variance model assumes that

the covariance matrix between assets is stable. In the

real market, covariances always change constantly,

especially during the epidemic period, so using a

simple covariance matrix to construct the portfolio is

not an accurate assessment of market performance. In

addition, the model building tool used in this paper is

Excel, not Python. large-scale data models are more

accurately and efficiently constructed in Python. And

the effective frontier graph which is showed does not

show in detail the changes in the Sharpe ratio of the

weights of the various assets, which is the limit of

Excel. As for the future research, it is a good attempt

to expand the data range to improve model accuracy

and explore the use of machine learning, artificial

intelligence, or tail risk management algorithms for

optimizing portfolios with new assets to address

market volatility.

4 CONCLUSIONS

To sum up, this study evaluates portfolio construction

using Markowitz's mean-variance theory, applying

two optimization objectives: maximizing the Sharpee

ratio and minimizing variance. The results indicate

that the portfolio optimized for maximizing the

Sharpee ratio can achieve the highest returns,

demonstrating its effectiveness in enhancing return

potential. In contrast, the minimum variance portfolio

provided greater stability, highlighting its advantage

in risk management. However, the study's limitations

include reliance on historical data and the omission of

new asset market impact, which may affect real-

world applicability. This research not only

demonstrates optimization methods for traditional

assets but also provides empirical support for

including new asset cryptocurrency in the portfolio. It

reveals how mean-variance theory can be applied to

diverse asset allocations to achieve higher risk-

adjusted returns, offering valuable insights for

investors navigating complex financial markets.

REFERENCES

Chen, J., Liu, Y., 2022. The Role of Cryptocurrencies in

Modern Portfolio Theory. Journal of Financial

Innovation, 9(3), 89-105.

Corbet, S., Meegan, A., Larkin, C., Lucey, B., Yarovaya, L.,

2018. Cryptocurrencies as a financial asset: A

systematic analysis. Journal of International Financial

Markets, Institutions & Money, 56, 1-22.

Fama, E. F., 1970. Efficient capital markets: A review of

theory and empirical work. Journal of Finance, 25*2,

383-417.

Fama, E. F., French, K. R., 1993. Common risk factors in

the returns on stocks and bonds. Journal of Financial

Economics, 33(1), 3-56.

Gorton, G., Rouwenhorst, K., 2021. Facts and Fantasies

about Commodity Futures. Financial Analysts Journal,

77(4), 40-54.

Guo, S., Lin, T., 2022. Big Data and Sentiment Analysis in

Portfolio Management. Financial Analysts Journal,

78(4), 102-118.

He, X., Liao, J., 2021. Machine learning for portfolio

optimization: An empirical study. Journal of Financial

Data Science, 3(1), 16-28.

Kahneman, D., Tversky, A., 1979. Prospect theory: An

analysis of decision under risk. Econometrica, 47(2),

263-292.

Klein, T., Thu, H. P., Walther, T., 2018. Bitcoin is not the

new gold – A comparison of volatility, correlation, and

portfolio performance. International Review of

Financial Analysis, 59, 105-116.

Liu, Y., Tsyvinski, A., 2021. Risks and returns of

cryptocurrency. The Review of Financial Studies, 113.

Markowitz, H. M., 1952. Portfolio selection. Journal of

Finance, 71, 77-91.

Sharpee, W. F., 1964. Capital asset prices: A theory of

market equilibrium under conditions of risk. Journal of

Finance, 19(3), 425-442.

Sullivan, R., Mackenzie, C., 2021. Sustainable Investing:

ESG Factors in Portfolio Construction. Global Finance

Journal, 50, 100-115.

Novel Portfolio Construction Based on Stocks, Traditional Stock Indices, Futures and Cryptocurrencies

179

Szymanowski, M., 2021. Commodities and Portfolio

Management: An Updated Analysis. Journal of

Commodity Markets, 15, 52-66.

VanEck. Bitcoin vs. Ethereum in 2024: Comparison &

outlook. VanEck. Retrieved from:

https://www.vaneck.com

Yahoo Finance. (n.d.). Yahoo Finance.

https://finance.yahoo.com/

Zhang, X., Liu, Z., 2023. Blockchain technology and its

implications for portfolio management. Journal of

Blockchain Research, 5(2), 45-62.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

180