The State-of-The-Art Price Prediction Scenarios: From Time Series

Methods to Deep Learning

Yulin Tang

The School of Finance, Shanghai University of International Business and Economics, Shanghai, China

Keywords: Price Forecasting, Time Series Analysis, Deep Learning, ARIMA, LSTM.

Abstract: As a matter of fact, stock price prediction is always one of the most challenge topics in finance fields.

Contemporarily, thanks to the rapid development of computer science, the prediction approaches have been

upgraded from time series models to deep learning scenarios. With this in mind, this study explores the latest

research progress in stock price prediction, particularly the application of time series analysis and deep

learning in this field. By comparing the autoregressive integrated moving average (ARIMA) model with the

long short-term memory (LSTM) model, this study analyses advantages and limitations of both models in

stock price prediction. Based on the evaluations, the research results show that the ARIMA model performs

stably in short-term prediction, while the LSTM model demonstrates strong long-term prediction ability in

complex market environments. At the same time, this study also discusses the challenges facing stock price

prediction and looks forward to the research direction of integrating multiple models to improve prediction

accuracy in the future.

1 INTRODUCTION

China Stock index fund has developed gradually

since 2002 and experienced many market ups and

downs and product innovations. Nowadays,

diversified products such as ETFs, general index

funds and index enhanced funds coexist, forming a

relatively complete investment system. However,

problems such as product homogeneity, vicious

competition, and insufficient investor education still

exist. Combined with the current development trend

of the financial market, it is predicted that index funds

will continue to optimize and innovate, while

strengthening supervision and investor education to

promote the healthy and stable development of the

market (Lai, 2023).

Considerable advancements have been made in

the realm of financial research pertaining to the

forecast of the price of stocks in the past few years,

especially driven by artificial intelligence technology.

On the basis of predecessors, scholars such as Ma

innovatively applied linear regression and random

forest model to the prediction of stock price trend and

proved the high efficiency of these methods in the

https://orcid.org/0009-0005-6035-8463

tasks of regression and classification through

empirical analysis (Ma, 2024). This research not only

enriches the theoretical system of financial

forecasting, but also provides scientific basis for

actual investment decision-making, and shows the

broad application prospect of artificial intelligence in

the financial field.

In the dynamic evolution of financial markets,

price forecasting becomes a key part of investment

strategy (Asghar et al., 2019). The objective of this

study is to investigate the potential applications of

time series analysis and deep learning techniques in

the domain of price prediction, with the ultimate goal

of enhancing the accuracy of prediction. Time series

method, with its solid statistical foundation, can

capture the temporal characteristics of market data.

Deep learning technology, with its powerful

nonlinear modelling ability, provides a new

possibility for price prediction in complex market

environment. This research framework considers the

two as complementary tools to build price forecasting

models together in order to achieve more accurate

forecasting in complex and volatile financial markets.

Tang, Y.

The State-of-the-Art Price Prediction Scenarios: From Time Series Methods to Deep Learning.

DOI: 10.5220/0013207500004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 117-122

ISBN: 978-989-758-726-9

117

2 DESCRIPTIONS OF MODELS

This study focuses on two models that have attracted

much attention in the field of stock prediction: the

autoregressive integral Moving average model

(ARIMA) based on time series analysis and the Long

short-term memory network (LSTM) model using

deep learning technology. With their unique

advantages, these two models show different

application potential and value in the volatility

prediction of stock market.

ARIMA Model (Autoregressive Integrated

Moving Average Model) is a classical method for

predicting and analysing non-stationary time series

data in the field of time series analysis. In stock

prediction, ARIMA model transforms non-stationary

stock price time series into stationary series through

difference technology, and then uses autoregression

(AR) and moving average (MA) parts to capture

autocorrelation and random error terms in the data.

Among them, the dependent variable is usually the

stock price or the rate of return, while the independent

variable includes the historical price data and its

difference, lag term, etc. The advantage of ARIMA

model is that it has a solid theoretical foundation and

good short-term prediction effect, but it may be

limited by the assumptions of stationarity and linear

relationship of data (Wu & Wen, 2016).

The LSTM model, or Long Short-Term Memory

network, is a special type of recurrent neural network

(RNN), which solves the gradient disappearance or

gradient explosion problem that traditional RNNS are

prone to when dealing with long sequences by

introducing a "gate" mechanism (forgetting gate,

input gate, output gate). In stock forecasting, LSTM

model can capture the long-term dependence of stock

price time series and effectively deal with the

nonlinear characteristics of the market. The inputs to

the model typically encompass market indicators

such as stock price, volume, opening price, closing

price, and so forth. In contrast, the output represents

the stock price or yield forecast at a specified future

point in time. The LSTM model offers significant

advantages in terms of its capacity for nonlinear

modelling and long-term information memory.

However, it is a highly computationally complex

model, and the parameters are challenging to adjust

(Peng, 2019).

In conclusion, the ARIMA and LSTM models

each possess distinctive advantages in the context of

stock forecasting. The former is more appropriate for

short-term scenarios with evident linear trends,

whereas the latter is better at addressing long-term,

non-linear and intricate market dynamics. According

to information characteristics and prediction needs,

the best model or mix of models can be chosen in

practice.

3 ARIMA

The ARIMA model is famous in time series analysis

and has several stock pricing prediction applications.

Officially, ARIMA is the Autoregressive Integrated

Moving Average Model. The formal representation of

the statistical model is ARIMA (p, d, q), whereby p

represents the quantity of autoregressive parts, d

denotes the degree of distinction, and q signifies the

quantity of moving average terms (Narendra &

Eswara, 2015; Zheng et al., 2016).

The model is ideal for non-stationary time series

data management. Data is converted into stationary

sequences using differencing techniques, allowing

predictive analysis. Practical ARIMA model

construction follows a disciplined process. A

stationarity test on the dataset using the Augmented

Dickey-Fuller (ADF) test is a first step. If the

variables are non-stationary, differencing is used until

they become stationary. The model orders p, d, and q

are determined by graphing the autocorrelation

function (ACF) and partial autocorrelation function

(PACF) or using information criteria like AIC and

BIC for model selection. Using historical data, the

model parameters are computed, and the fit is

assessed. The application of residual analysis enables

the evaluation of the model's capacity to successfully

record the latent information within the dataset. The

ARIMA model can predict stock prices using

previous stock price data. An ARIMA model using

historical closing price data for a corporation

illustrates this notion. The model predicts future price

values and confidence intervals within a given

timeframe. The projected results may help investors

make informed investment strategy decisions.

Upon examination of the data shown in Table 1

and Table 2, it is evident that the ARIMA (3,1,1)

model exhibits the most minimal P-value, which is

below the preset significance threshold of 5%.

Furthermore, upon conducting a comparative

examination of various statistical indicators, it

becomes apparent that the ARIMA (3,1,1) model has

greater performance in comparison to the other three

models. Significantly, it demonstrates the greatest F-

statistic of 9.814915 in comparison to the other two,

accompanied by the lowest P-value. Therefore,

within the framework of generating short-term

predictions for the Huatai Securities Index, this

research utilized the ARIMA (3,1,1) model as the

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

118

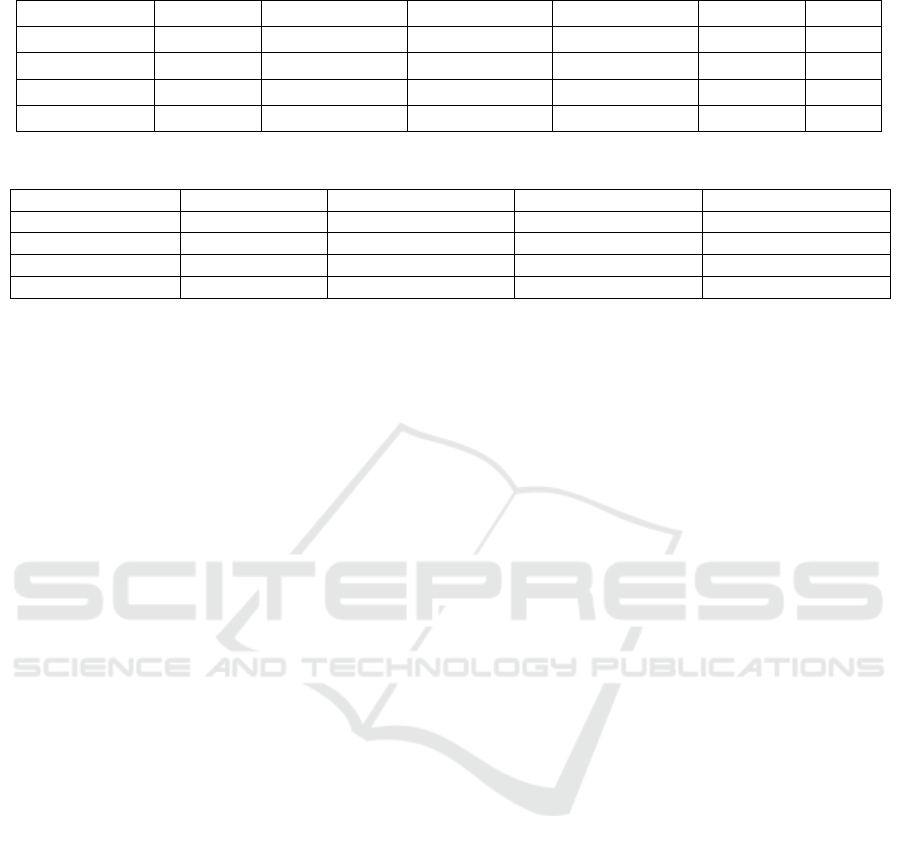
Table 1: Comparison of P-values of equations.

P value C ar(1) ar(3) ar(6) ma (1) ma (3)

ARIMA (1,1,1) 0.0800 0.6667 --- 0.6206 ---

ARIMA (3,1,1) 0.0420 --- 0.0232 ___ 0.0001 ---

ARIMA (3,1,1) 0.0194 --- 0.0049 --- --- 0.0521

ARIMA (6,1,1) 0.1068 --- ___ 0.0287 0.0008

Table 2: Comparison of precision indexes of various models.

Metrics ARIMA (1,1,1) ARIMA (3,1,1) ARIMA (3,1,3) ARIMA (6,1,1)

AIC 1.980981 1.969110 2.014602 1.982976

SC 2.024360 2.012748 2.058229 2.027008

F-statistic 7.327459 9.814915 4.130716 5.316455

Prob(F-statistic) 0.000816 0.000080 0.017248 0.006008

selected predictive modelling approach (Zhou et

al.2018). The findings reported in this study

demonstrate the efficacy of ARIMA models in

precisely forecasting short-term market trends,

effectively capturing the volatile nature of stock

values. Nevertheless, it is crucial to acknowledge that

ARIMA models must account for significant

disparities in long-term forecasts for stock markets

due to their inherent intricacy and uncertainty. In this

particular scenario, the experiment was only based on

the Huatai Securities Index as a fundamental

benchmark. Hence, in practical situations, it is

imperative to integrate supplementary analytical

methodologies and techniques to enhance the

accuracy and reliability of forecasts.

In conclusion, ARIMA models are widely

recognized as extremely efficient instruments for

conducting time series analysis and possess

considerable significance within the domain of stock

prediction. By meticulously constructing models and

subsequently adapting them to real-world scenarios,

it is possible to provide investors with comprehensive

decision-making support.

4 LSTM

When discussing stock price prediction, while the

ARIMA model is widely employed due to its

simplicity and effectiveness in short-term trend

forecasting, modern deep learning technologies,

especially Long Short-Term Memory (LSTM)

networks, have introduced a new perspective into this

domain. As a variant of Recurrent Neural Networks

(RNNs), the LSTM model excels in addressing long-

term dependencies within time series data, rendering

it a highly promising tool for stock price prediction

(Yao, 2024). The LSTM model effectively avoids the

problems of gradient vanishing or gradient explosion

that usually happen with RNNs during long sequence

training by using memory cells, forget gates, input

gates, and output gates, among other things. In stock

prediction, The LSTM has the ability of tracking the

long-term dependencies in stock price movements

and providing precise predictions while incorporating

recent market dynamics (Lahboub & Benali, 2024).

To apply LSTM for stock price prediction, the

following process is typically followed: Firstly, stock

price data is collected and preprocessed, including

cleaning and normalization, to ensure data quality.

Secondly, a predictive feature set is constructed

through technical analysis or automatic feature

extraction methods. Next, the LSTM model

architecture is designed, involving the determination

of the quantity of network layers and neurons, as well

as the selection of activation functions and

optimization algorithms. The model is then trained

using the training set data, with iterative optimization

enhancing prediction performance. Subsequently, the

model's accuracy is evaluated using the test set, often

through metrics such as Mean Squared Error (MSE)

and Root Mean Squared Error (RMSE). Finally,

investment strategies are formulated based on the

model's predictions, with their effectiveness verified

in actual trading. The LSTM model uses MSE as a

loss function to evaluate its performance during

training. MSE is a widely employed technique for

quantifying the difference between the anticipated

values of a model and the actual outcomes, with a

lower MSE indicating more accurate predictions.

In Experiment E, the research team directly

employed Mean Squared Error (MSE) as the loss

function, combining historical market data with

corresponding technical indicators to train the Long

Short-Term Memory (LSTM) network. Seen from

Table 3, the results indicated that the LSTM model

utilizing MSE as the loss function demonstrated high

The State-of-the-Art Price Prediction Scenarios: From Time Series Methods to Deep Learning

119

accuracy and stability in reproducing common

trading signals such as crossover strategies and

Moving Average Convergence Divergence (MACD)

strategies. In practical applications, the LSTM model

has showcased robust predictive capabilities (Troiano,

2019). Through deep mining and learning of

historical stock data, the model can capture intricate

patterns of stock price movements and exhibit high

accuracy in forecasting future stock prices (Galegale

& Shimabukuro, 2024).

In summary, the LSTM model serves as an

effective tool in the field of stock prediction within

deep learning, with broad application prospects. By

continuously optimizing the model structure and

training strategies, LSTM is poised to provide

investors with more precise and efficient stock

prediction services.

Table 3: Analysis of Accuracy and Training Methods in Experiment E.

1—DIRECT USEFULINFORMATION

Output Loss Crossover MACD

Train Test Epochs Train Test Epochs

C MSE 0.9892 0.9895 5798 0.9724 0.7948 4884

士 0.36% 士 0.91% ±1267 ±1.00% ±12.33% ±1953

U MSE 0.9877 0.9907 5769 0.9931 0.8907 5998

士 0.56% ±0.79% 士 1133 士 0.36% 士 5.52% ±1776

U CE 0.9896 0.9889 5254 0.9966 0.9264 6563

0.0037

±1.00% ±1046 士 0.22% 土 4.25% 士 1804

2—DIRECT USEFUL INFORMATION AND UNRELATEDINDICATORS

C MSE 0.9922 0.9596 2984 0.9835 0.781 3507

士 0.41% ±2.14% 士 354 ±0.66% ±8.68% ±707

U MSE 0.9925 0.9557 3107 0.9917 0.7679 2862

士 0.44% ±1.99% 士 531 ±0.41% ±11.00% 士 222

U CE 0.9917 0.9609 2973 0.9966 0.7744 2924

士 0.53% 士 1.98% ±357 士 0.27% ±10.52% 士 305

3—CORRELATED INFORMATION

C MSE 0.9738 0.6817 3194 0.9675 0.6664 3972

士 0.35% ±14.27% 士 933 ±1.09% ±15.21% ±1051

U MSE 0.9739 0.6939 3781 0.9747 0.6941 3588

士 0.38% ±13.36% ±1296 士 0.95% ±11.66% ±1430

U CE 0.9741 0.7965 4184 0.984 0.731 3322

0.0038

士 12.06% ±1401 ±0.59% ±12.53% 士 839

4—CORRELATED INFORMATIONAND UNRELATED INDICATORS

C MSE 0.9899 0.8967 2774 0.9751 0.6199 3405

士 0.42% 士 5.34% 士 126 土 0.890 ±17.19% ±709

U MSE 0.9896 0.9061 2959 0.9828 0.6394 2933

士 0.31% ±3.65% 土 424 ±0.79% ±11.48% 士 408

U CE 0.9911 0.8877 3173 0.9899 0.6032 2934

士 0.49% 士 7.33% ±737 士 0.58% ±16.27% 士 295

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

120

5 LIMITATIONS AND

PROSPECTS

The landscape of stock forecasting has undergone

significant transformations, yet it remains a complex

and multifaceted domain fraught with obstacles.

Among these hurdles, overfitting remains a

paramount challenge, plaguing even the most

sophisticated forecasting models. Traditional tools of

time series analysis, notably the ARIMA model, have

long been the stalwarts of financial forecasting, adept

at unravelling the intricacies of linear and stationary

time series patterns. However, their efficacy wanes in

the face of the highly nonlinear and turbulent nature

of financial markets, where they often struggle to

encapsulate the full spectrum of dynamic behaviours,

thereby inviting the spectre of overfitting and

compromising predictive accuracy.

Conversely, the emergence of the LSTM model

has ushered in a new era of possibilities in financial

forecasting. Its prowess in capturing long-term

dependencies and retaining memory across data

sequences grants it a unique advantage in unravelling

patterns that would otherwise be elusive to traditional

methods. This capability, coupled with its

effectiveness in processing sequential data, positions

the LSTM as a formidable contender in the realm of

stock predictions. Nevertheless, even the LSTM is not

immune to the perils of overfitting, particularly when

confronted with limitations in training data or

suboptimal feature selection. Moreover, the

intricacies of its architecture and the substantial

computational resources it demands can present

barriers to its widespread deployment.

To overcome these limitations and propel the field

of stock forecasting forward, a more holistic approach

is imperative. This necessitates the fusion of diverse

methodologies, harnessing the strengths of each to

create a robust hybrid forecasting framework. By

blending the stability and reliability of traditional

models like ARIMA, which excel in handling

stationary time series, with the adaptability and

pattern recognition capabilities of the LSTM,

researchers can forge a forecasting system that is both

precise and resilient. This hybrid approach has the

potential to enhance predictive accuracy while

mitigating the risk of overfitting, thereby broadening

the model's generalization capabilities. Furthermore,

as the realms of big data and intelligent systems

continue to expand, the inclusion of diverse data

sources and the development of innovative

algorithms offer unprecedented opportunities for

advancing stock predictions. By leveraging these

advancements, researchers can delve deeper into the

complexities of financial markets, incorporating real-

time information, historical trends, and even external

factors to create more nuanced and accurate forecasts.

The adoption of advanced regularization techniques

and data augmentation strategies, which go beyond

conventional methods, is also crucial in safeguarding

against overfitting and ensuring the robustness of

forecasting models.

Basically, the trajectory of stock prediction hinges

upon the amalgamation of various approaches, the

application of cutting-edge technologies, and a

constant dedication to innovation. By embracing this

holistic approach, researchers can anticipate

significant breakthroughs in predictive accuracy,

empowering investors with the knowledge and

insights they need to navigate the intricate landscape

of financial markets with greater precision and

confidence.

6 CONCLUSIONS

To sum up, this study rigorously scrutinizes the

effectiveness of time series analysis and deep learning

technologies in the field of stock market forecasting.

It contrasts the ARIMA model, which demonstrates

proficiency in short-term predictions under stable

market conditions, with the LSTM model, an

advanced neural network variant renowned for its

ability to handle complex, non-linear dynamics,

making it particularly suitable for longer-term

forecasts. Despite their distinct advantages, both

models encounter common challenges, including the

risks of overfitting to historical data and the

computational strain associated with complex

algorithms. To address these limitations, the paper

calls for future research to focus on integrating the

unique strengths of multiple models, such as

combining the stability of ARIMA with the

adaptability of LSTM and broadening the scope of

data sources to include macroeconomic indicators

and investor sentiment analysis, thereby improving

overall prediction accuracy and reliability. This study

not only contributes to the theoretical understanding

of stock market dynamics but also offers practical

insights and methodological guidance for investors

seeking to navigate the complexities of financial

markets, highlighting its significant implications for

informed decision-making.

The State-of-the-Art Price Prediction Scenarios: From Time Series Methods to Deep Learning

121

REFERENCES

Asghar, M. Z., Rahman, F., Kundi, F. M., Ahmad, S., 2019.

Development of stock market trend prediction system

using multiple regression. Computational and

Mathematical Organization Theory, 19, 3.

Galegale, N., Shimabukuro, C. I., 2024. Deep Learning

Applied to Stock Prices: Epoch Adjustment in Training

an LSTM Neural Network. International Journal of

Business and Management, 19(4).

Lahboub, K., Benali, M., 2024. Assessing the Predictive

Power of Transformers, ARIMA, and LSTM in

Forecasting Stock Prices of Moroccan Credit

Companies. Journal of Risk and Financial

Management, 17(7), 293.

Lai, X. P., 2023. The dev elopment status, problems, and

countermeasures of China's stock index funds. Banker,

12.

Ma, J. J., 2024. Research on regression and classification

in stock price trend prediction. Computer Knowledge

and Technology, 12.

Narendra B. C., Eswara, R., B. 2015. Prediction of selected

Indian stock using a partitioning-interpolation based

ARIMA-GARCH model. Applied Computing

Informatics, 112.

Peng, Y., Liu, Y. H., Zhang, R. F., 2019. Modeling and

analysis of stock price prediction based on LSTM.

Computer Engineering and Applications, 11, 7.

Troiano, L., Mejuto V. E., Loia, V., 2018. Replicating a

trading strategy by means of lstm for financial industry

applications. IEEE Transactions on Industrial

Informatics, 3226-3234.

Wu, Y. X., Wen, X., 2016. Short-term stock price

prediction based on ARIMA model. Statistics and

Decision, 23.

Yao, X., 2024. LSTM Model enhanced by Kolmogorov-

Arnold network: improving stock price prediction

accuracy. Trends in Social Sciences and Humanities

Research, 4, 19.

Zheng, T., Farrish, J., Kitterlin, M.,2016. Performance

trends of hotels and casino hotels through the

recession: An ARIMA with intervention analysis of

stock indices. Journal of Hospitality Marketing

Management, 251, 49-68.

Zhou, X., Pan, Z., Hu, G., Tang, S., Zhao, C., 2018. Stock

market prediction on high-frequency data using

generative adversarial nets. Mathematical Problems in

Engineering, 4, 1-11.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

122