Reevaluating Stock Price Prediction: The Influence of Machine

Learning on Forecast Accuracy

Yingqian Cao

School of Engineering, Carnegie Mellon University, Pittsburgh, PA, U.S.A.

Keywords: Stock Price, Machine Learning, Time Series Regression, Data Analysis.

Abstract: Due to the complexity and volatility of financial markets, traditional methods have often failed, prompting

the adoption of advanced machine learning techniques that leverage vast datasets and sophisticated

algorithms for improved forecast accuracy. This research aims to compare traditional and advanced machine

learning techniques in predicting equity premiums, a crucial metric in financial economics. Using a

comprehensive dataset encompassing various economic and financial indicators, this study initially

implemented a rolling linear regression model as a baseline, followed by more sophisticated models,

including Bagged Trees. Model performance was assessed using Out-of-Sample (OOS) R-squared (R

Mean Absolute Error (MAE), and Root Mean Squared Error (RMSE). The results showed that the Bagged

Trees model exhibited the most reliable performance, the Rolling Linear Regression model followed, with

the Long Short-Term Memory (LSTM) model being the least effective. The inherent unpredictability of

equity premiums is attributed to limited access to comprehensive market information, the noisy and

complex nature of financial markets, and the over-fitting tendency of advanced models. To enhance

predictive accuracy, future research should consider integrating alternative data sources, employing

advanced noise-filtering techniques, developing hybrid models, applying robust regularization methods and

creating dynamic models that adapt to evolving market conditions.

1 INTRODUCTION

In the dynamic world of finance, accurately

predicting stock prices has long been a challenging

yet essential endeavor for investors, analysts, and

financial institutions. Traditional methods, relying

heavily on historical data and linear models, have

often fallen short in capturing the complex and

volatile nature of stock markets (Mehra et al., 2003).

In this situation, the advent of machine learning has

ushered in a new era of stock price prediction (Gu et

al., 2020). By leveraging advanced algorithms and

vast datasets, machine learning techniques promise

to enhance forecast accuracy significantly.

Within the prediction of different metrics in

financial economics, equity premiums have always

been a longstanding topic. The equity premium

refers to the excess return that investing in the stock

market offers over a risk-free rate. Researchers have

explored various models and methods to predict

equity premiums, yielding mixed results. Early

studies on equity premium prediction primarily

focused on historical averages. Numerous studies

have explored the use of economic and financial

indicators to predict equity premiums. Fama and

French demonstrated that dividend yields and

earnings-price ratios possess predictability for future

equity premiums (Fama et al., 1996). Similarly,

Campbell and Shiller showed that the ratio of stock

prices to dividends could forecast long-term returns

(Campbell et al., 1988).

Despite these findings, the predictability of such

indicators remains debated. Goyal and Welch

critically reviewed several predictive variables and

found that many failed to outperform simple

historical averages Out-Of-Sample (OOS) (Welch et

al., 2008). Their findings cast doubt on the reliability

of traditional economic and financial indicators for

equity premium prediction. Researchers have also

investigated the role of macroeconomic variables in

predicting equity premiums. Lettau and Ludvigson

proposed the consumption-wealth ratio as a predictor,

demonstrating its effectiveness in forecasting future

returns (Lettau et al., 2001). However, the

predictability of macroeconomic variables is not

universally accepted. Ang and Bekaert found that

while certain macroeconomic factors could predict

IS returns, their OOS performance was often poor

Cao, Y.

Reevaluating Stock Price Prediction: The Inﬂuence of Machine Learning on Forecast Accuracy.

DOI: 10.5220/0013207000004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 85-91

ISBN: 978-989-758-726-9

(Ang et al., 2007). This inconsistency has fueled

ongoing debates about the practical utility of

macroeconomic variables in equity premium

prediction.

Over the past decade, artificial intelligence has

advanced rapidly, leading to the creation of

increasingly sophisticated data analysis techniques.

Recent advancements in machine learning and

statistical methods have opened new avenues for

predicting equity premiums. For instance, Gu et. al.

utilized machine learning techniques to analyze a

vast array of predictors, demonstrating improved

OOS performance compared to traditional models

(Gu et al., 2020). Their findings suggest that

machine learning can uncover complex patterns in

the data that conventional methods might miss.

Recurrent Neural Networks (RNNs) and bagged

trees are widely used in various fields. For example,

when predicting the future probability of

environmental factors, RNNs serve as an effective

tool, combining the learning capabilities of feed-

forward neural networks with enhanced expressive

power through dynamic equations (Chen et al.,

2018); bagged tree model can be used to map

landslide susceptibility (Wu et al., 2020). Given the

success of these models in predicting time-

dependent variables in different contexts, there is

significant potential for using these models to

predict equity premiums, which are also time-

dependent variables.

This study aims to introduce linear regression

model and advanced machine learning techniques to

predict stock prices for performance comparison.

The predictions are, in turn, evaluated with OOS R-

squared value (R

), Mean Absolute Error (MAE),

and Root Mean Squared Error (RMSE).

2 METHOD

2.1 Dataset Preparation

In this study, the equity premium dataset is used for

stock prices’ evaluating (Welch et al., 2008). The

data is related to equity premium with prominent

variables, which stores 1, 620 records (i.e., one

instance per month) and covers 17 columns. All

variables are numerical fields. Based on the equity

premium dataset, 14 different explanatory variables

are recreated such as inflation and stock variance

(Welch et al., 2008).

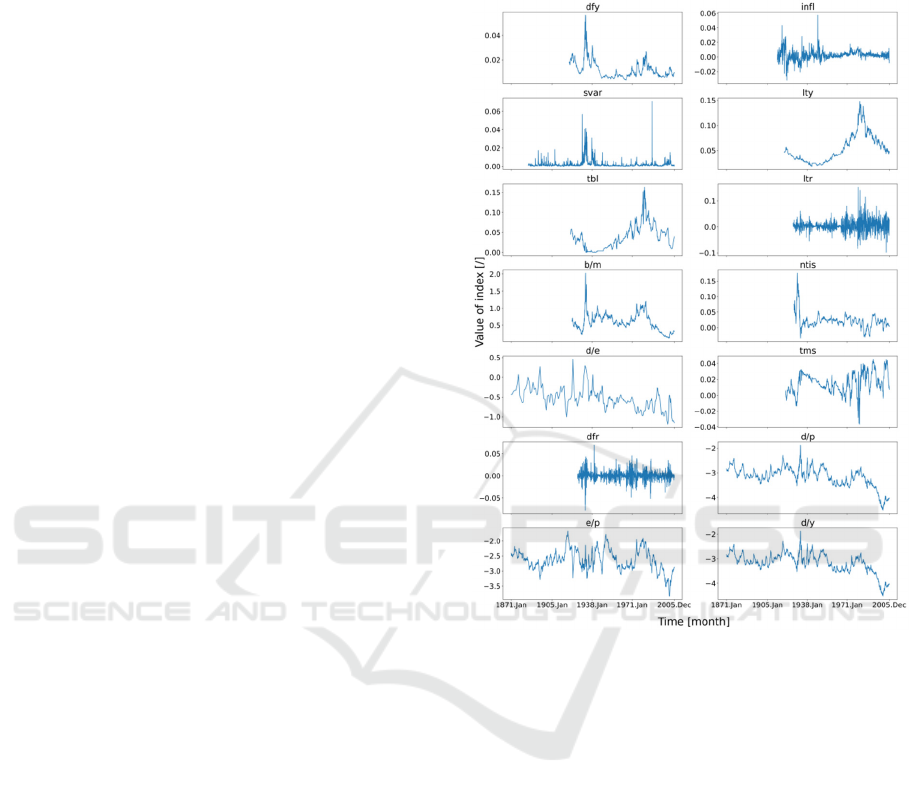
In order to understand the extreme values and

temporal trend of the data, the data was plotted, as

shown in Figure 1.

Figure 1: Explanatory variable against time (1871 - 2005)

(Welch et al., 2008).

2.2 Machine Learning-based Prediction

In this part, rolling linear regression model is used to

replicate and verify the conclusions in the work

carried out by Welch et al. (Welch et al., 2008).

Then, two advanced models (RNNs and bagged tree)

are used to improve and recreate R

, RMSE and

MAE values.

2.2.1 Linear Regression-based Prediction

Rolling linear regression model fits regressions to a

window of data, continuously updating the model as

the window shifts forward over time. The illustration

of rolling multiple linear regression model is shown

in Figure 2.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

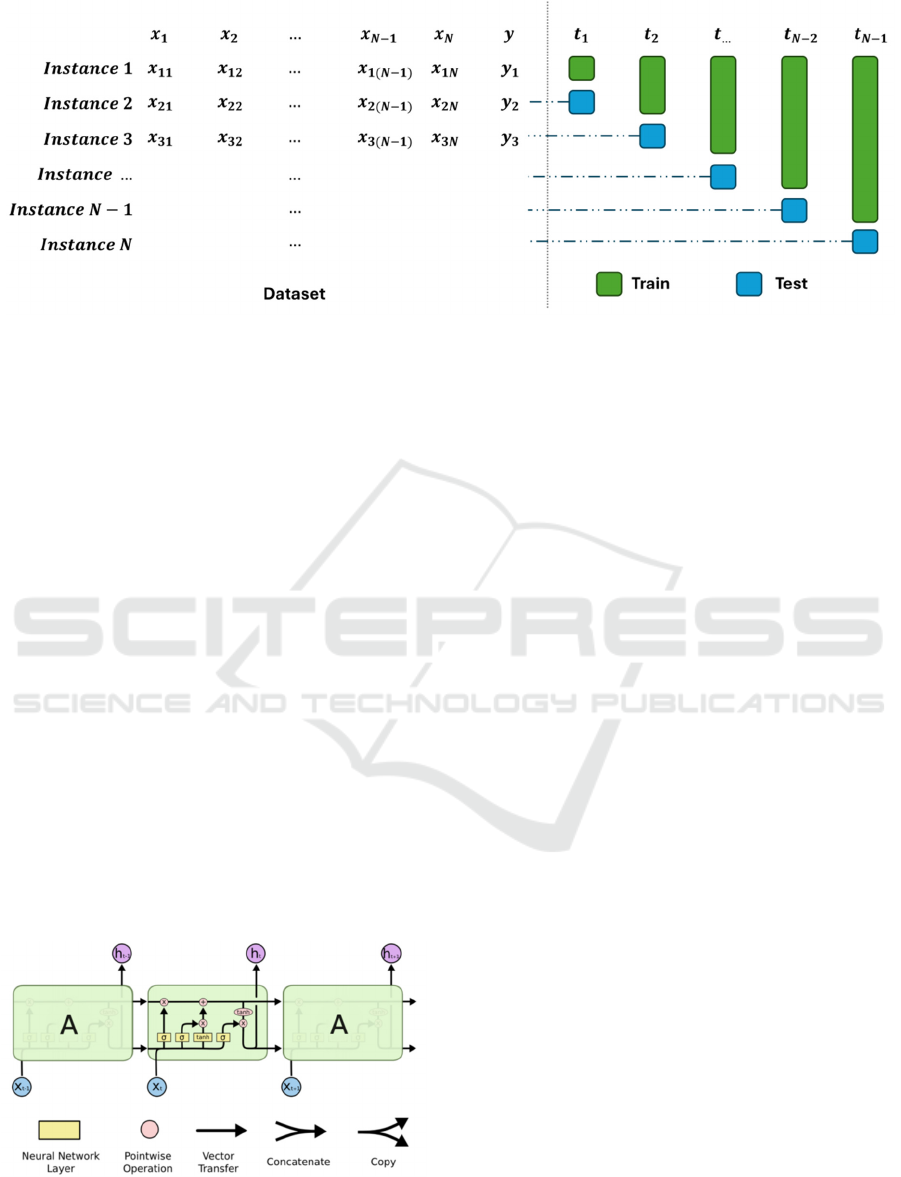
Figure 2: Illustration of the Model (Photo/Picture credit: Original).

Using a rolling linear regression model offers

several advantages. This approach allows for

dynamic analysis by enabling model parameters to

change over time, thus capturing evolving

relationships between variables. It also aids in

detecting structural changes or breaks in the data,

providing insights into periods of instability or shifts

in underlying processes. Additionally, it improves

model robustness by reducing the impact of outliers

and anomalies, ensuring reliability even with

unusual data points. In this part, the model does not

require the determination of any extra parameters.

2.2.2 LSTM

RNNs generate and retain memory of previous states

throughout the feed-forward process. The

mechanism of Long Short-Term Memory (LSTM), a

specific type of RNN, is illustrated in Figure 3.

LSTM models offer several advantages, such as

managing long-term dependencies and overcoming

the vanishing gradient problem typical in traditional

RNNs. Additionally, LSTMs can handle variable-

length sequences and provide robust performance in

both directions.

Figure 3: Interacting layers in an LSTM (Thorir, 2021).

In this part, the model is trained with a hidden

state of 256 neurons, learning rate of 6 ൈ 10

ିସ

weight decay of 5 ൈ 10

ି଺

, 15 epochs. All data

points are used at each epoch.

2.2.3 Bagged Trees Model

Bootstrap aggregating, commonly known as bagging,

is an ensemble meta-algorithm in machine learning

that enhances the stability and accuracy of

algorithms used for classification and regression.

While typically applied to decision tree methods,

bagging can be utilized with any machine learning

algorithm (Opitz et al., 1999).

Decision tree models offer several advantages.

Firstly, they are easy to understand and interpret.

This makes decision trees particularly useful for

explaining model predictions to stakeholders.

Additionally, they can handle non-linear

relationships between features and target variables,

which is beneficial for datasets with complex

interactions. Lastly, decision trees are versatile and

can be used with both numerical and categorical data,

adding to their flexibility and ease of use in various

applications.

In this part, a bagging ensemble model uses

decision trees to predict the equity premium, where

the base estimators are set to 500; when looking for

the best split, number of features to consider is set to

0.5.

3 RESULTS AND DISCUSSION

3.1 Model Performance

The true data and predicted values of each model is

plotted against time, are shown in Figure 4, Figure 5,

Reevaluating Stock Price Prediction: The Inﬂuence of Machine Learning on Forecast Accuracy

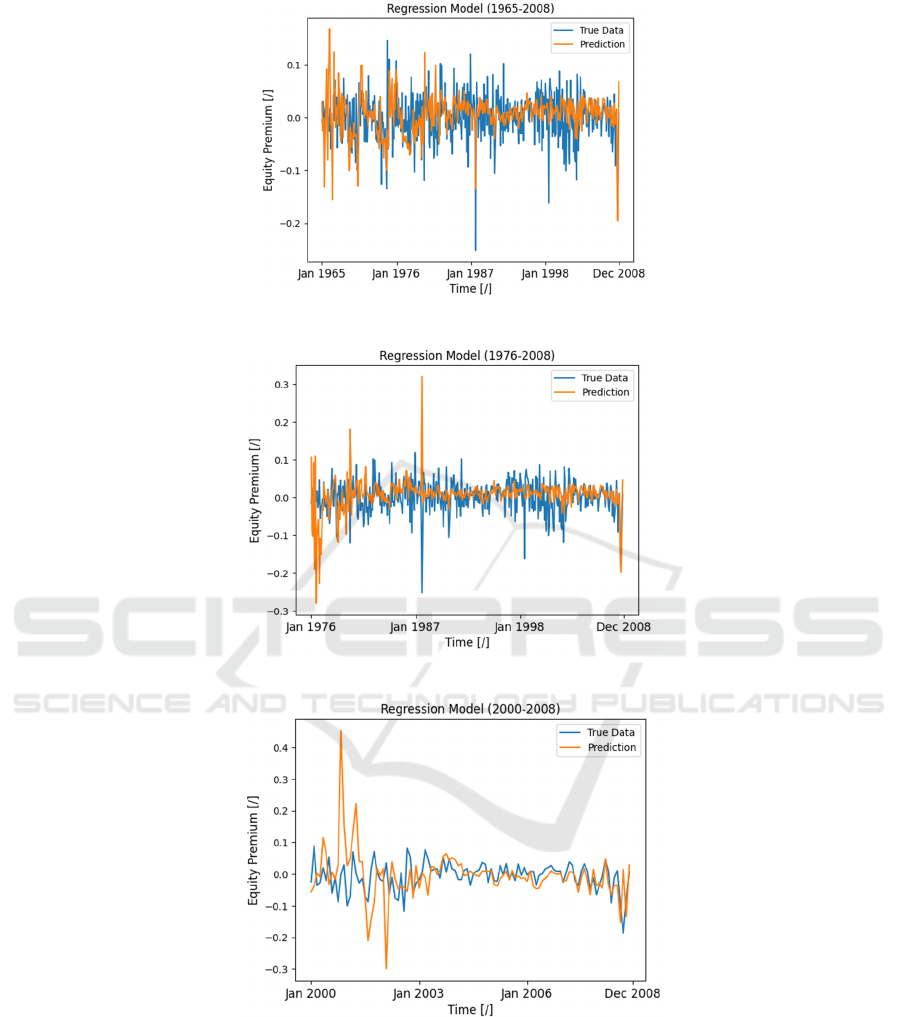
Figure 4: Performance for linear regression (1965-2008) (Photo/Picture credit: Original).

Figure 5: Performance for linear regression (1976-2008) (Photo/Picture credit: Original).

Figure 6: Performance for linear regression (2000-2008) (Photo/Picture credit: Original).

Figure 6, Figure 7, Figure 8, Figure 9, Figure 10,

Figure 11 and Figure 12.

From the plots of rolling linear regression shown

in Figure 4, Figure 5 and Figure 6, the true data and

predictions align closely, suggesting potential over-

fitting in the model. During the 1965-2008 period,

the actual data shows the highest equity premium

around 1987, whereas the model's predictions

indicate peaks around 1965 and 2008. In the 1976-

2008 period, the true label of the largest equity

premium (negative) occurs around 1987, but the

model predicts the highest premiums around 1976

(positive) and 2008. For the 2000-2008 period, the

true data exhibits relatively stable equity premiums,

while the model forecasts significant peaks in 2001

(positive) and 2002 (negative).

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

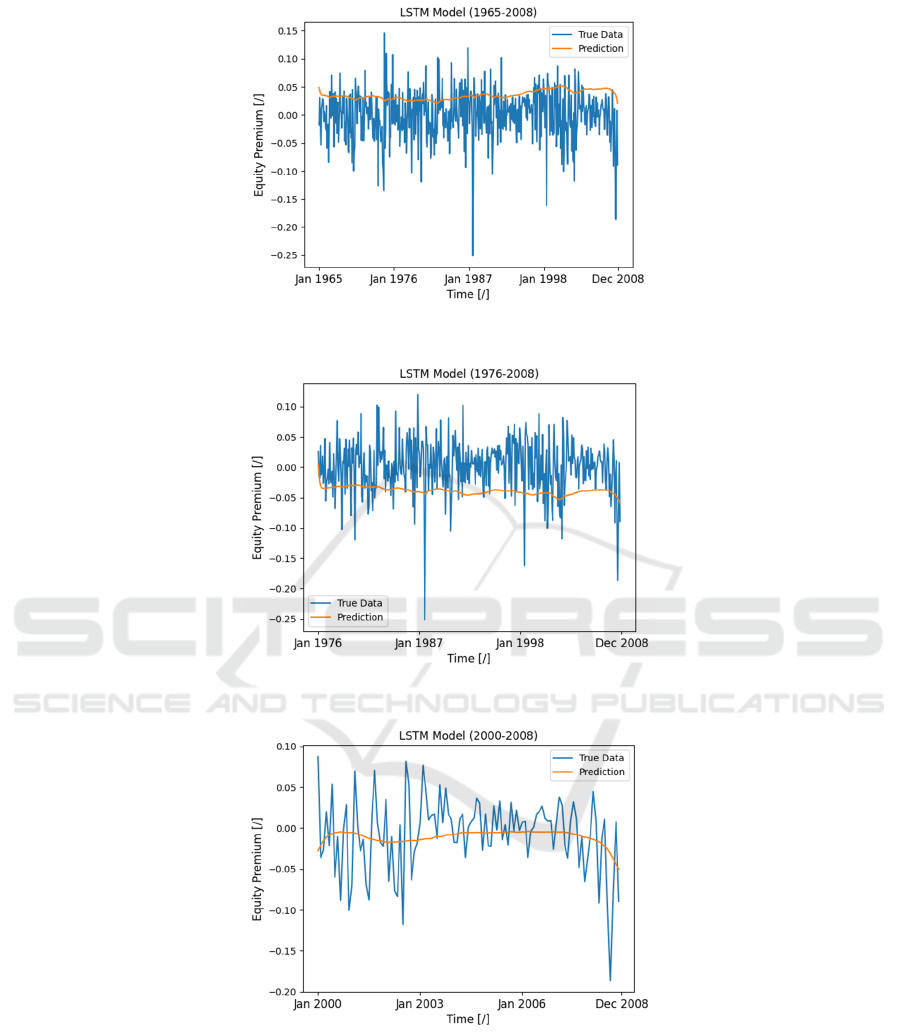
Figure 7: Model performance for LSTM (1965-2008) (Photo/Picture credit: Original).

Figure 8: Model performance for LSTM (1976-2008) (Photo/Picture credit: Original).

Figure 9: Model performance for LSTM (2000-2008) (Photo/Picture credit: Original).

The plots shown in Figure 7, Figure 8 and Figure

9 demonstrate that the bidirectional LSTM model no

longer exhibits over fitting but fail the capture the

trend across most of the periods studied. In the

1965-2008 and 1976-2008 periods, as well as the

2000-2008 period, the predictions generally do not

follow the rise and fall of the actual equity premium.

Reevaluating Stock Price Prediction: The Inﬂuence of Machine Learning on Forecast Accuracy

Figure 10: Performance for bagged trees (1965-2008)

(Photo/Picture credit: Original).

Figure 11: Performance for bagged trees (1976-2008)

(Photo/Picture credit: Original).

Figure 12: Performance for bagged trees (2000-2008)

(Photo/Picture credit: Original).

The plot shown in Figure 10, Figure 11 and

Figure 12 shows that while the predictions from the

decision tree model generally follow the same

pattern as the true data, there are frequent and abrupt

fluctuations in the predictions that do not align

smoothly with the equity premium’s trend. Although

the model captures some of the general rise and fall

of the true data, these frequent, jagged movements

suggest that the decision tree model is not a suitable

method for reliable equity premium forecasting.The

irregular pattern of the predictions suggests that this

model is overly sensitive to changes in the training

data and does not capture the underlying market

dynamics consistently or meaningfully.

3.2 Evaluation Metrics

A horizontal comparison of metrics for model

evaluation was calculated, as listed in Table 1, Table

2 and Table 3.

Table 1: R-squared distributions.

Period

Rolling Linear

ression model

LSTM

model

Bagging

Tree model

1965-

2008

0.034 -0.673 -0.0810

1976-

2008

-0.837 -0.8195 -0.092

2000-

2008

-2.312 0.0648 -0.1617

Table 2: RMSE distributions.

Period

Rolling Linear

ression model

LSTM

model

Bagging

Tree model

1965-

2008

0.043 0.0569 0.0021

1976-

2008

0.059 0.0589 0.0021

2000-

2008

0.081 0.0437 0.0024

Table 3: MAE distributions.

Period

Rolling Linear

ression model

LSTM

model

Bagging

Tree model

1965-

2008

0.032 0.0440 0.0342

1976-

2008

0.037 0.0493 0.0344

2000-

2008

0.049 0.0332 0.0351

The bagging tree model is the most reliable,

despite its negative R-squared values, followed by

the rolling linear regression model, with the LSTM

model being the least effective.

The performance differences among the models

can be attributed to several factors. The rolling linear

regression model tends to overfit historical data,

capturing noise rather than underlying trends, and

lacks the flexibility to model non-linear relationships

and complex market dynamics. Additionally, its

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

assumption of parameter stability over time does not

hold well in the volatile stock market, reducing

predictive accuracy. The LSTM model, while

designed to handle long-term dependencies,

struggled with capturing equity premium trends due

to its high data and hyperparameter tuning

requirements, and its sensitivity to sequence length.

The bagged trees model, on the other hand, benefits

from capturing complex interactions and non-linear

relationships through ensemble learning, reducing

over-fitting and variance. However, it exhibited

frequent abrupt fluctuations, indicating noise

sensitivity and potential over-fitting to training data,

along with insufficient temporal adaptation,

affecting its long-term prediction reliability. These

differences indicated by its negative R-squared

values, which highlight the inherent unpredictability

of the equity premium.

3.3 Discussion

The unpredictability of the equity premium is due to

several factors: limited access to comprehensive

information in real-world markets, the inherent noise

and complexity of financial markets exhibiting non-

stationary and chaotic behaviors, and the simplicity

of the models used in the analysis, which lack the

sophisticated optimization of Genetic Algorithms-

enhanced (GAs-enhanced) models. Additionally, the

tendency of complex models to over-fit historical

data can result in poor generalization in OOS

predictions.

The current implementation is not without areas

to improve. First, incorporating alternative data

sources, such as sentiment from social media or

news, could provide more insights and improve

predictions. Second, advanced noise-filtering

techniques like wavelet transforms or Kalman filters

could help isolate useful patterns from market noise.

Third, using hybrid models and advanced

optimization techniques like GAs may enhance

model performance. Moreover, future research

should also focus on preventing over-fitting by

applying better regularization methods and using

robust validation techniques. Developing dynamic

models that adapt to changing market conditions,

such as those using reinforcement learning, could

also lead to more accurate predictions.

4 CONCLUSIONS

This study reevaluated stock price prediction by

comparing the performance of traditional and

advanced machine learning techniques. A rolling

linear regression model and advanced models such

as LSTM and bagged trees were used to predict

equity premiums, evaluating their performance using

OOS-R

, RMSE, and MAE. This study concludes

that while advanced machine learning models offer

improved performance metrics, the equity premium

remains fundamentally challenging to predict

accurately. Contributing factors to this

unpredictability include limited access to

comprehensive information, the inherent noise and

complexity of financial markets, the simplicity of

models used, and the over-fitting tendency of

complex models on historical data. To improve

future predictions, incorporating alternative data

sources, advanced noise-filtering techniques, hybrid

models, and better regularization methods, as well as

developing dynamic models that adapt to changing

market conditions, are recommended.

REFERENCES

Ang, A., & Bekaert, G. 2007. Stock return predictability:

Is it there? The Review of Financial Studies, 20(3),

651-707.

Campbell, J. Y., & Shiller, R. J. 1988. The dividend-price

ratio and expectations of future dividends and discount

factors. The review of financial studies, 1(3), 195-228.

Chen, Y., Cheng, Q., Cheng, Y., Yang, H., & Yu, H. 2018.

Applications of recurrent neural networks in

environmental factor forecasting: A review. Neural

Computation, 30(11), 2855-2881.

Fama, E. F., & French, K. R. 1996. Multifactor

explanations of asset pricing anomalies. The Journal

of Finance, 51(1), 55-84.

Gu, S., Kelly, B., & Xiu, D. 2020. Empirical asset pricing

via machine learning. The Review of Financial Studies,

33(5), 2223-2273.

Ingolfsson, T. M. 2021. Insights into LSTM architecture.

Retrieved from https://thorirmar.com/post/insight_into_

lstm/

Lettau, M., & Ludvigson, S. 2001. Consumption,

aggregate wealth, and expected stock returns. the

Journal of Finance, 56(3), 815-849.

Mehra, R., & Prescott, E. C. 2003. The equity premium in

retrospect. Handbook of the Economics of Finance, 1,

889-938.

Opitz, D., & Maclin, R. 1999. Popular ensemble methods:

An empirical study. Journal of Artificial Intelligence

Research, 11, 169-198.

Welch, I., & Goyal, A. 2008. A comprehensive look at the

empirical performance of equity premium prediction.

The Review of Financial Studies, 21(4), 1455-1508.

Wu, Y., Ke, Y., Chen, Z., Liang, S., Zhao, H., & Hong, H.

2020. Application of alternating decision tree with

AdaBoost and bagging ensembles for landslide

susceptibility mapping. Catena, 187, 104396.

Reevaluating Stock Price Prediction: The Inﬂuence of Machine Learning on Forecast Accuracy