Machine Learning Implementation for Demand Forecasting in

Supply Chain Management

Yumo Bai

Department of Economics, University of California San Diego, San Diego, U.S.A.

Keywords: Demand Forecasting, Machine Learning in Retail, ARIMA Model, XGBoost Algorithm.

Abstract: This paper aims to enhance demand forecasting accuracy in retail supply chains with the application of

machine learning techniques: Autoregressive Integrated Moving Average (ARIMA) and XGBoost models. In

this respect, the research addressed shortcomings of traditional approaches to forecasting, very often missing

the complexity of modern demand patterns due to their reliance on historical data and simplistic assumptions.

While the ARIMA model would model seasonality in time series data, the XGBoost would model more

complex and nonlinear interactions among multiple features. The dataset was sourced from Kaggle. Treatment

of missing values and outliers was handled, and further enhancement by feature engineering was added. The

results indicate that while ARIMA is very effective in capturing temporal dependencies and seasonal trends,

XGBoost outperforms it in handling complex relationships that deal with fuel prices and CPI. Indeed, the

combination of both models makes for a holistic model toward demand forecasting, illustrating substantial

improvements in the accuracy of the forecast. This can be taken as proof that by combining these methods,

the retailing sector might come up with efficient inventory management strategies. Further work could also

aim at incorporating more sources of external data into the model, and model scaling to allow real-time usage.

1 INTRODUCTION

Demand forecasting has been identified as the driver

of supply chain management with regard to inventory

optimization, operational efficiencies, and customer

satisfaction. This would help the company in

optimizing inventory levels, hence reducing costs,

and this has huge implications for practice. A correct

forecast ensures adequate availability of products,

reduces costs related to overstocking and

understocking, and raises the overall satisfaction level

of the customers by setting productions and inventory

strategies in accordance with the actual market

demand.

The recent advances that have been in machine

learning open an avenue of promise for alternative

solutions to the traditional approaches (Lin et al.,

2024). This is because the traditional approaches, on

many occasions, have failed to capture the

complexity and dynamics that characterize modern

demand patterns because they are coupled with over-

reliance on statistical modeling and reliance upon

manual working processes. These traditional

https://orcid.org/0009-0000-7169-2444

methods, in their own ways, are restrictive, for they

build up the forecast based on historic demand

information and are inherently inclined to make

simple assumptions that do not account for

complicated market trends, promotional activities,

and other exogenous economic leading indicators

(Ampazis, 2015). Machine learning models, on the

other hand, can deal with large data sets, identify

patterns that are complex, and deliver trustworthy

forecasts. It can help in replacing the existing

lackluster traditional forecast processes. For instance,

Arif et al. demonstrated that machine learning

algorithms, such as K-Nearest Neighbors, Support

Vector Machines, and Gaussian Naive Bayes,

significantly improve demand forecasting accuracy in

retail supply chains (Arif et al., 2019).

However, there are still some major gaps in

existing research. Firstly, most existing models have

limited the integration of multiple external factors. In

other words, for such factors as temperature and

unemployment rate, how they dynamically interact

Bai, Y.

Machine Learning Implementation for Demand Forecasting in Supply Chain Management.

DOI: 10.5220/0013206900004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 77-84

ISBN: 978-989-758-726-9

with each other to influence sales forecasting is less

investigated by existing models. For example, Wu

and Coggeshall showed that proper cross-validation

techniques can guarantee that the model does not get

overfitted and remains flexible to demand patterns by

touting regression, neural networks, and decision

trees (Wu and Coggeshall, 2012). However, there is a

lack of research on how these engineered features

could be optimized and dynamically adjusted

according to changing market conditions. Moreover,

the feature importance analysis for the existing

research was very less comprehensive. For example,

Chen and Guestrin have demonstrated that factors

like an unemployment rate and fuel price are

influential in demand forecasting using the Gradient

boosting Model (GBM) (Chen and Guestrin, 2016).

However, little has been done in terms of exploring

feature extraction and selection methods with a view

to improving the performance of forecasting. In view

of this, according to this study, a more comprehensive

approach will be adapted with further adjustments

and treatments in data processing and model

selection.

This paper is geared toward developing a machine

learning model that improves the accuracy of demand

forecasting for any retail company. The

Autoregressive Integrated Moving Average model

(ARIMA) will be chosen specifically for this project

to model time series data with strong seasonal

patterns. According to Shukla, this model has very

good predictive performance on such data (Shukla,

2020). The study will also include extreme Gradient

Boosting as a supplement, which helps capture

complicated and nonlinear interactions between

features. While XGBoost and GBM are both

implementations of the gradient boosting algorithm,

the former will be chosen because it has built-in

cross-validation and early stopping functions. Thus,

additional lines of code for cross-validation and early

stopping would not be needed, making model

validation and parameter tuning relatively easy. This

makes it easier to avoid model overfitting during the

training process. Obviously, these models

complement each other in functionality. For instance,

an ARIMA model is used to model time series data in

the first place, this should capture the trend and

cyclical changes of the data. In this respect, based on

the ARIMA model, an XGBoost model may further

deal with the residues in order to improve the

accuracy of the whole prediction. Their combination

may, therefore, give rise to a comprehensive retail

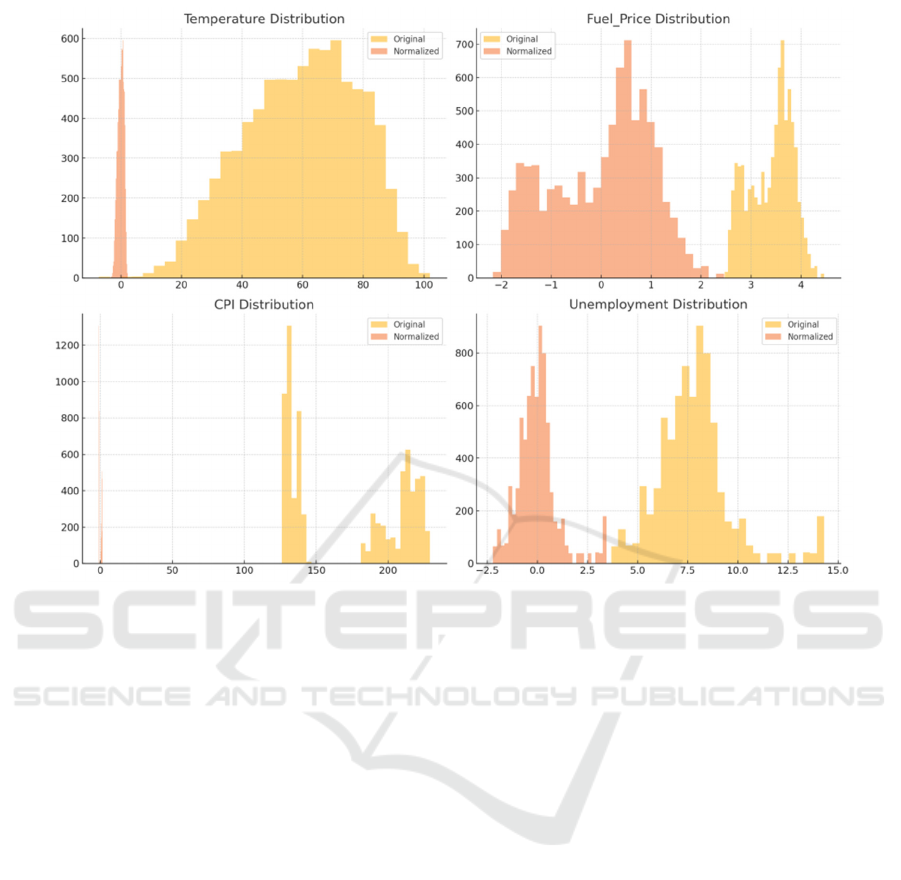
Figure 1: Comparison of Original and Normalized Distributions for Selected Features (Photo/Picture credit: Original).

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

demand forecasting method, improving operational

efficiency and enhancing strategic decision-making

in inventory management.

METHOD

2.1 Dataset Preparation

The dataset for this research is obtained from Kaggle

(Ahmedov, 2022). This dataset contains details of 12

fields and 8,190 records, capturing important factors

such as temperature and fuel price, markdowns,

Consumer Price Index (CPI), and unemployment rate

that could impact the sale. This involved dealing with

missing values, outliers, and normalization. Missing

values in the MarkDown field were replaced with the

median to reduce skewness. Outliers were treated

using the process of the Interquartile Range (IQR)

and were also subjected to Winsorization to minimize

the inflating effects outliers had on the model.

Numerical features were then scaled to zero mean and

unit variance, using Sklearn library's StandardScaler.

This procedure will make learning more efficient and

increase model precision. Figure 1 show the

comparison of raw and standardised distributions of

some features.

Feature engineering is an important step to

improve forecast accuracy, which creates rolling

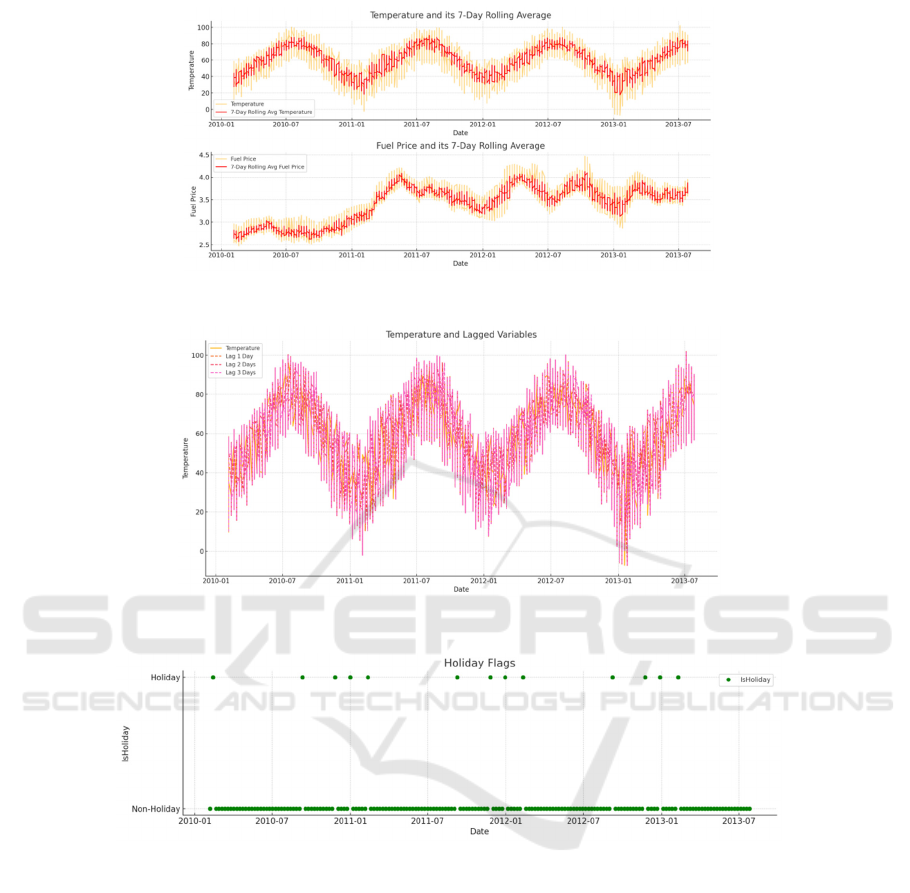
Figure 2: Temperature and Fuel Price with their respective 7-day rolling averages (Photo/Picture credit: Original).

Figure 3: The distribution of temperature and lagged variables (Photo/Picture credit: Original).

Figure 4: The distribution of Holiday Flags (Photo/Picture credit: Original).

Machine Learning Implementation for Demand Forecasting in Supply Chain Management

means and lagged variables to capture short-term

fluctuations and time dependence, respectively (Wu

& Coggeshall, 2012). It involved creating rolling

averages and lagged variables to capture short-term

fluctuations and temporal dependencies. Rolling

averages for temperature and fuel prices over a 7-day

window helped smooth out short-term noise and

highlight long-term trends. Lagged variables for

temperature, fuel prices, and markdowns were

created to capture both short-term and slightly longer-

term dependencies. In addition, a binary flag variable,

IsHoliday, was introduced to account for the effects

of holidays on sales patterns in this study. The

processed dataset now contains 22 fields, including

the original and preprocessed features. The processed

dataset will be trained with an 80:20 train-test split for

easy model evaluation. Figures 2, Figure 3 and Figure

4 illustrate the application of rolling averages and

lagged variables to smooth and capture the temporal

dependencies in the data. The codes of ARIMA

model and XGBoost are both from open-source files

on github (dmlc, 2021; Shukla, 2024).

2.2 ARIMA Combined GBM Model

2.2.1 Introduction of ARIMA

ARIMA is a well-proven statistical method widely

used in forecasting time series. The acronym stands

for AutoRegressive (AR) terms, integrated (I) terms,

and Moving Average (MA) terms combined in the

analysis of trends (Shukla, 2020). The AR part

models the variable on its own lagged values, the

integrated terms add differencing in the data to

achieve stationarity, and the MA part models the error

term as a linear combination of the error terms that

occurred contemporaneously and at various times in

the past (Shukla, 2020). As suggested by Shukla

(2020), ARIMA has been considered an appropriate

model in demand forecasting with a strong data trend

or seasonal pattern. For instance, in predicting the

level of retail sales, ARIMA can be fitted to historical

sales data showing apparent seasonal fluctuations

(Shukla, 2020). An ARIMA equation will compute

future behavioral models that correctly predict future

peaks and troughs in sales (Shukla, 2020). This

application in real life manifests the capacity of

ARIMA to model complex seasonal behaviors in time

series data; hence, it makes a very suitable choice for

this project, where historical sales data present a very

significant seasonal pattern because of holidays and

promotional activities. Through ARIMA, this study

could capture such temporal patterns, thus increasing

the accuracy of the short-term forecasts.

2.2.2 Introduction of GBM

XGBoost is a powerful machine learning technique

designed to scale and efficiently deal with large-scale

datasets and complex relationships in data. In this

setting, it forms an ensemble of weak learners—

usually decision trees—where each successive tree

tries to rectify the mistakes made by its predecessor.

As Chen and Guestrin point out, XGBoost provides

state-of-the-art results for a range of machine learning

problems in terms of scalability, efficiency, and the

ability to handle sparsity (Chen & Guestrin, 2016, p.

786). The dataset is also significant for nonlinear

interactions among features with broad predictors

considered in the case, such as temperature, fuel

prices, CPI, and markdowns. Moreover, XGBoost

allows insights into the importance of features, such

that one can identify the most important drivers of

demand and those that would guide strategic

decision-making. What makes it perfect for this

project is its proven performance in many

competitions and its ability to scale across distributed

environments, just as Chen and Guestrin had said—

strong and malleable (Chen & Guestrin, 2016).

2.2.3 Implementation Details

In this project, ARIMA and XGBoost are applied

complementarily to leverage their strengths. ARIMA

focuses on modeling the temporal dependencies of

sales data, representing seasonal trends and periodic

fluctuations. The model will work well on short-term

forecasts, where knowing past trends is very

important. XGBoost is utilized in the modeling of

complex interactions in a rich set of engineered

features against the target variable, using lagged

variables and rolling averages, along with holiday

flags. This builds on the flexibility and complexity of

the model that captures intricate patterns in the

driving of demand, thus leading to accuracy in

forecasting. Finally, this study tested the robustness

and the right prediction power of the models through

a solid validation strategy that includes cross-

validation and out-of-sample testing. Performance

measures showing the goodness of fit to the model are

Mean Absolute Error (MAE), Root Mean Square

Error (RMSE), and combined with residual analysis

to confirm the adequacy of the models. So, by

comparing those metrics, this project can determine

which model is more effective under different

scenarios and refine the approach accordingly.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

3 RESULTS AND DISCUSSION

3.1 The Performance of the Model

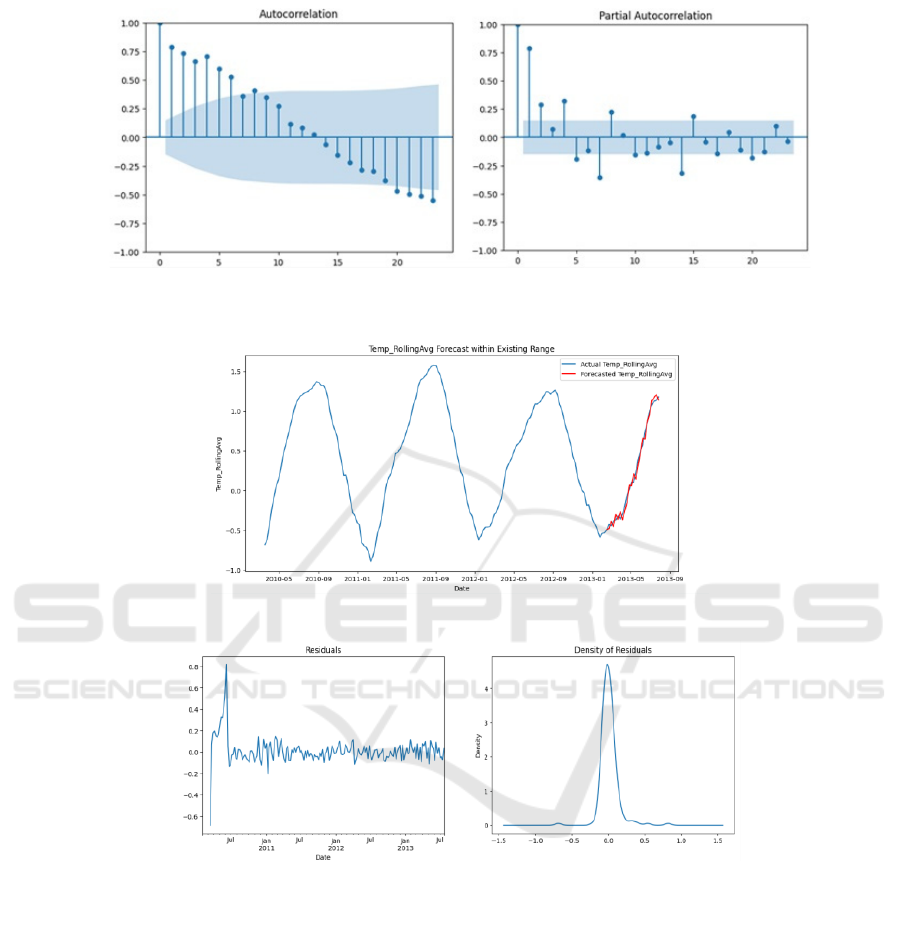
The ARIMA model was tested for stationarity using

the Augmented Dickey–Fuller (ADF) test during

development. The ADF test resulted in a statistic of -

3.936202 with a p-value of 0.001784, which led to the

rejection of the null hypothesis of non-stationarity.

This confirmed that the differenced series was

appropriate for ARIMA modeling. The identification

of the ARIMA model's order was guided by the

Autocorrelation Function (ACF) and Partial

Autocorrelation Function (PACF) plots. As shown in

Figure 5 and Figure 6, the ACF plot showed a slow

decay, suggesting a moving average component in the

model, while the PACF plot indicated that an

autoregressive component of order 1 would be

suitable. Thus, an ARIMA (1,1,1) model was selected

for further analysis. The model was trained on the

Temp_RollingAvg and Fuel_Price_RollingAvg

series, with significant autoregressive (AR. L1 =

0.9504, p < 0.001) and moving average (MA. L1 = -

0.4306, p < 0.001) coefficients.

Figure 5: Autocorrelation Function (ACF) Plot and Partial Autocorrelation Function (PACF) Plot for Temp_RollingAvg

(Photo/Picture credit: Original).

Figure 6: Forecast of Temp_RollingAvg within Existing Range (Photo/Picture credit: Original).

Figure 7: Residuals and Density of Residuals for Temp_RollingAvg Forecast (Photo/Picture credit: Original).

Machine Learning Implementation for Demand Forecasting in Supply Chain Management

The model's predictive ability was validated by

comparing forecasts to actual data from February 15,

2013, to July 26, 2013. The forecasts closely followed

the actual observations, particularly in the latter part

of the series, as shown in Figure 6. This close

agreement demonstrates that the ARIMA model

effectively captured the underlying patterns,

including trends and seasonal components. The

model's MAE was 0.060637, and the RMSE was

0.066666, indicating a good fit. Residual analysis, as

presented in Figure 7, further validated the model's

performance. The residuals showed initial volatility

but later stabilized around zero, indicating that the

ARIMA model effectively captured the data's

patterns without leaving out systematic components.

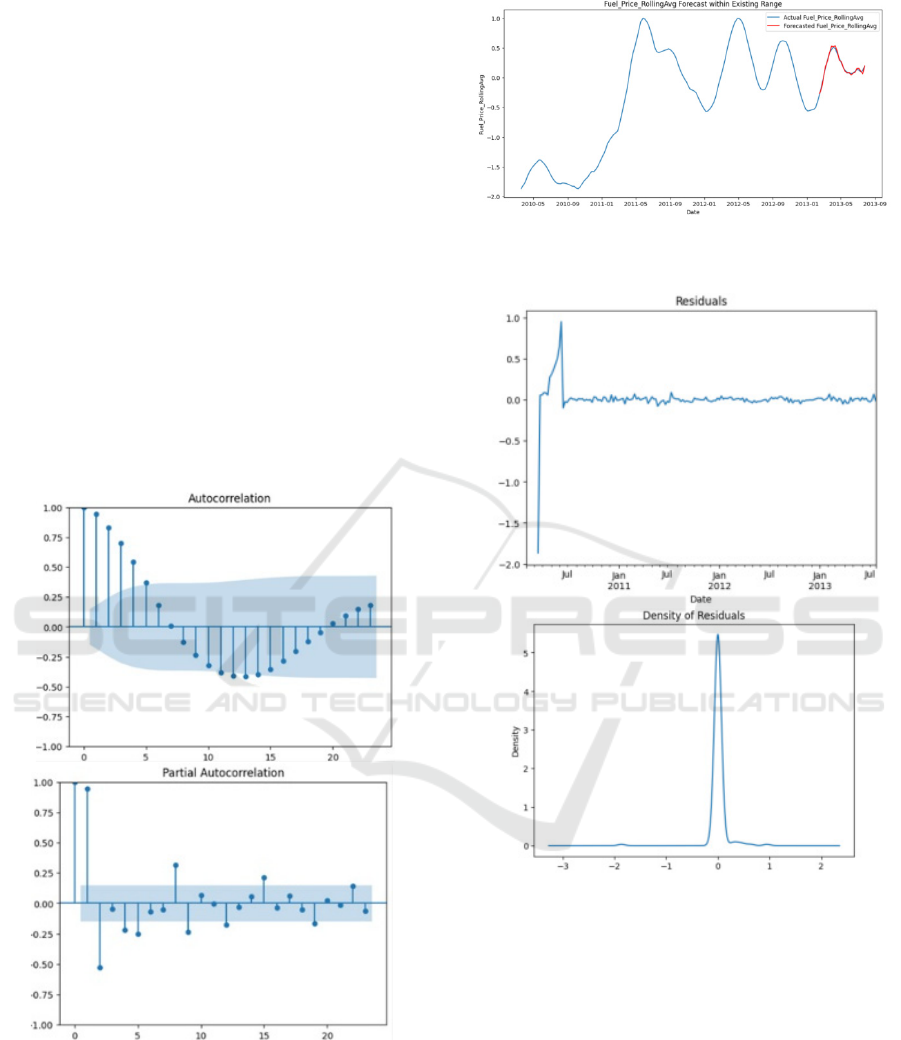
The model's application to the

Fuel_Price_RollingAvg series showed similarly

strong predictive power, with supporting evidence

from ACF and PACF plots, forecast, and residual

analyses (Figure 8, Figure 9 and Figure 10).

Figure 8: Autocorrelation Function (ACF) Plot and Partial

Autocorrelation Function (PACF) Plot for

Fuel_Price_RollingAvg (Photo/Picture credit: Original).

Figure 9: Forecast of Fuel_Price_RollingAvg within

Existing Range (Photo/Picture credit: Original).

Figure 10: Residuals and Density of Residuals for

Fuel_Price_RollingAvg Forecast (Photo/Picture credit:

Original).

The XGBoost model utilized 100 estimators with

a learning rate of 0.1. The model's predictive

performance, evaluated by MAE (0.36085) and

RMSE (0.50281), indicated reasonable accuracy.

While it captured the overall trend, particularly for

Fuel_Price, fluctuations in CPI predictions were less

accurate, as shown in Figure 11 and Figure 12.

Residual analysis, depicted in Figure 13 and Figure

14, revealed a random distribution around zero for

CPI and Fuel_Price, indicating unbiased predictions.

The feature importance analysis of the XGBoost

model (shown in Figure 15) identified unemployment

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

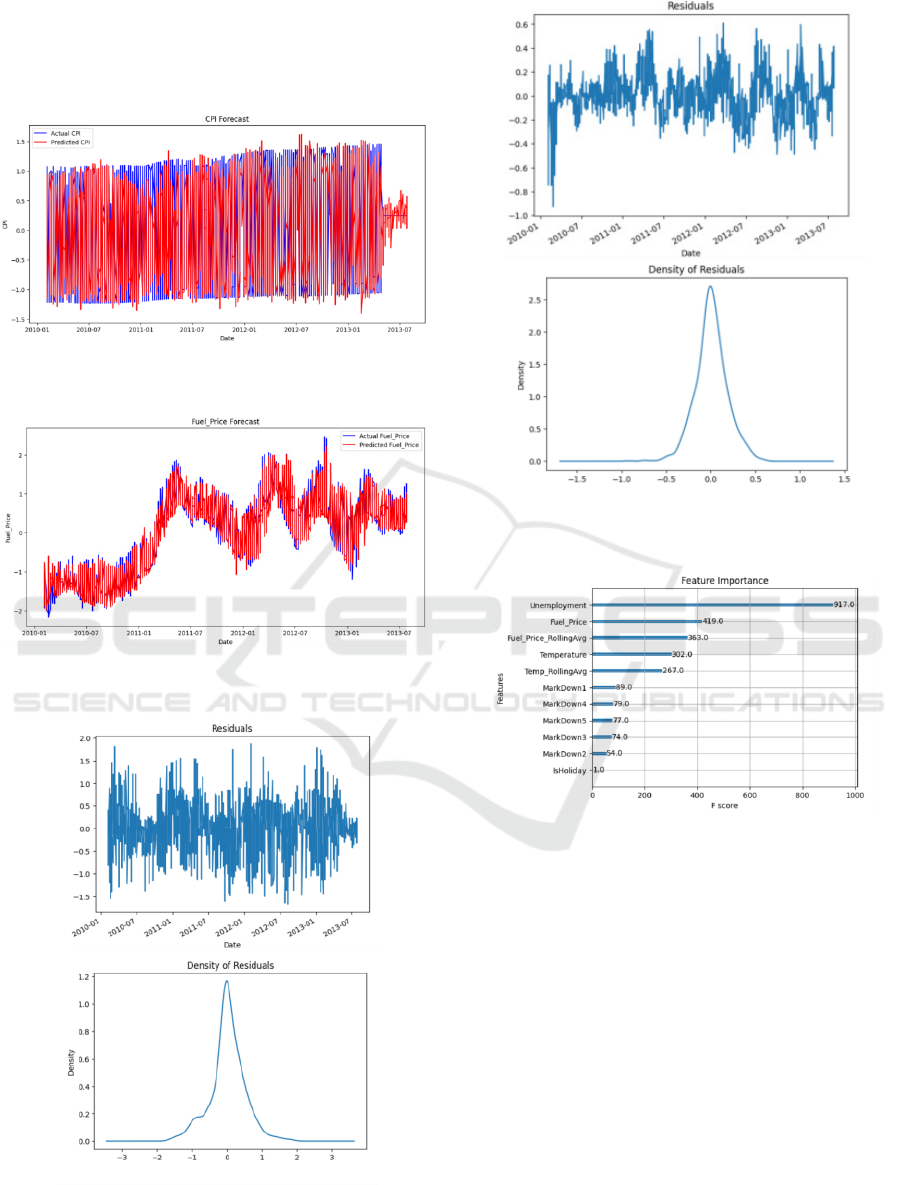
rate as the most important factor influencing the CPI

and forecasts. These insights are valuable for

improving forecasting strategies and improving the

decision-making process.

Figure 11: Actual vs. Predicted CPI Values (Photo/Picture

credit: Original).

Figure 12: Actual vs. Predicted Fuel_Price Values

(Photo/Picture credit: Original).

Figure 13: CPI Residual Analysis and Density Plot

(Photo/Picture credit: Original).

Figure 14: Fuel_Price Residual Analysis and Density Plot

(Photo/Picture credit: Original).

Figure 15: CPI Feature Importance Plot (Photo/Picture

credit: Original).

3.2 Discussion

The results of this study further confirm the

significance of the ARIMA model in capturing

seasonal trends and temporal dependencies within

data, while the XGBoost model is much more adept

at handling complex and nonlinear relationships.

More importantly, this research illustrates the

complementary advantages of the two models over

different aspects of demand forecasting. This thus

insinuates that a hybrid model—capitalizing on the

strong points of the ARIMA and XGBoost—may be

critical to overcoming a myriad of challenges

characterizing the modern retail environment.

Machine Learning Implementation for Demand Forecasting in Supply Chain Management

These findings also support some of the prior

studies, confirming and giving further insight into

these models' applications in demand forecasting. For

example, this study can be deemed to extend the work

of Arif et al. In such respect, they were able to

demonstrate that machine learning algorithms were

indeed capable of making retail demand forecasts

(Arif et al., 2019). Their research, however, was

limited to less complex data sets where the

relationship among variables was more direct. Based

on this, this paper further elaborates on the detailed

dynamics of complex reality through the division of

complex data into two categories, linear and

nonlinear, and applies two advanced machine

learning algorithms with different logics: ARIMA

and XGBoost.

In addition, the findings from this study also

connect to Frank's research. He added that if the

models were to be well trained and validated, then

machine learning models would improve demand

forecast accuracy based on different prevailing

factors (Frank, 2022). In light of this research, the

XGBoost algorithm was used to determine drivers of

demand, like unemployment and fuel prices, and

provide reliable forecasts in this paper. This is

evidenced by the random distribution of residuals

around zero and the normal distribution of errors. It is

further added to the ability of the model in terms of

providing actionable intelligence for the process of

decision-making by feature importance analysis.

4 CONCLUSIONS

This paper focuses on the development of machine

learning models for demand forecasting within a

retail context in a bid to optimize inventory

management. The main aim is to be able to come up

with good demand forecasts that result in balancing

stock levels, reducing costs due to overstocking and

understocking while increasing customer satisfaction.

This work improves the accuracy of demand

forecasting by using machine learning techniques in

time series analysis, ARIMA and XGBoost, for

capturing complex interactions between different

features. Reflecting on this project, future research

can incorporate more external data sources to

improve the robustness and accuracy of the prediction

model. For instance, in the forecasted weather aspect

for assessing the impact on sales, real-time weather

data would be most effective in capturing the direct

effects on consumer behavior. The most troublesome

parts that occurred in completing this project were the

size limitation of the dataset and missing values. This

is why data augmentation and synthetic data

generation are promising research paths. Last,

attention should be paid to the model's scalability and

deployment in a real-world environment. This could

involve a real-time prediction framework with

automatic model retraining to keep it up-to-date and

accurate over time.

REFERENCES

Ahmedov, A. 2022. Walmart Sales Forecast: Walmart Sales

Forecasting A CRISP-DM Model [Data set]. Kaggle.

Retrieved June 27, 2024, from

https://www.kaggle.com/datasets/aslanahmedov/walm

art-sales-forecast

Ampazis, Nicholas. 2015. Forecasting Demand in Supply

Chain Using Machine Learning. International Journal

of Artificial Life Research, 5(1), 85.

Arif, M. A. I., Sany, S. I., Nahin, F. I., & Rabby, A. S. A.

2019. Comparison study: product demand forecasting

with machine learning for shop. In 2019 8th

International Conference System Modeling and

Advancement in Research Trends (SMART) (pp. 171-

176). IEEE.

Chen, T., & Guestrin, C. 2016. Xgboost: A scalable tree

boosting system. In Proceedings of the 22nd acm

sigkdd international conference on knowledge

discovery and data mining (pp. 785-794).

Dmlc. 2021. XGBoost [Source code]. GitHub. Retrieved

Aug 2, 2024, from https://github.com/dmlc/xgboost.

Frank, Edwin. 2022. Leveraging Machine Learning to

Improve Demand Forecasting for Production Planning

and Inventory Optimization. Journal of Supply Chain

Management, 22(3), 5.

Lin, Z., Zhu, G., Deng, Y., Chen, X., Gao, Y., Huang, K.,

& Fang, Y. 2024. Efficient parallel split learning over

resource-constrained wireless edge networks. IEEE

Transactions on Mobile Computing.

Sarangkartikey50. 2016. Stock prediction time series

analysis [Source code]. GitHub. Retrieved June 26,

2024, from https://github.com/sarangkartikey50/stock-

prediction-time-series-analysis

Shukla, P. 2024. Ultimate guide for ARIMA time series

forecasting. Dataaspirant. Retrieved June 26, 2024,

from https://dataaspirant.com/arima-time-series-

forecasting/

Wu, J., & Coggeshall, S. 2012. Foundations of predictive

analytics. CRC Press.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence