Machine Learning for Smart Cities: LSTM Model-Based Taxi OD

Demand Forecasting in New York

Ziyan Chen

Information Management and System, Shanghai University, Jiading, Shanghai, China

Keywords: Taxi OD Demand Forecasting, LSTM Model, Machine Learning, Model Optimization.

Abstract: This study delves into the realm of advanced machine learning techniques, with a particular focus on

employing the Long Short-term Memory Network (LSTM) model for forecasting Taxi Origin-Destination

(OD) demand in New York City. In the quest for the most accurate predictive model, this paper conducted a

comparative analysis between the Decision Tree (DT), Random Forest (RF), and the aforementioned LSTM

model. The findings of this study reveal that the LSTM model outperforms its counterparts in both prediction

accuracy and generalization capability. The model's coefficient of determination (R²) stands at an impressive

0.9657, signifying that it captures a substantial 96.57% of the variance within the dataset. Through model

optimization, this study has further minimized the error index, highlighting the sensitivity of the model to its

configuration and the potential for enhanced performance. As looking towards the horizon, future research

endeavors will concentrate on overcoming current limitations and bolstering the robustness and applicability

of the LSTM model. The further study plans to extend its application to various urban settings and integrate

real-time data streams to augment its predictive prowess. Additionally, examining the model's efficacy in a

multi-modal traffic context and exploring the synthesis of LSTM with other machine learning algorithms to

forge hybrid models could lead to the development of more sophisticated and precise demand forecasting

tools. These advancements will be instrumental in facilitating smarter urban transport planning and

management, thereby revolutionizing the way approaching Taxi OD demand forecasting in the era of machine

learning.

1 INTRODUCTION

The progression of smart city development has

positioned the sophistication and efficacy of urban

transportation systems as key performance indicators

of urban advancement. In the vibrant epicenter of

global economic and cultural activity that is New

York City, the fine-tuning of its transportation

infrastructure is of utmost importance. Since the turn

of the decade, there has been a discernible downturn

in the prevalence of the iconic yellow taxis, while the

adoption of app-based ride-hailing services has

experienced a meteoric rise, culminating in a record

92.5 million passengers in 2016 (New York City

Government, 2017). This surge is mirrored by a

twofold increase in the registration of rental vehicles,

including both taxis and private car services, which

underscores the burgeoning demand for a multiplicity

of rental vehicle services. These data collectively

https://orcid.org/0009-0003-0792-9947

delineate a trend where the sharing economy and the

proliferation of mobile technology are propelling a

pronounced preference for the convenience and

efficiency of online ride-hailing services.

The forecasting of Taxi Origin-Destination (OD)

demand is a pivotal component of intelligent

transportation systems, tasked with the precision

prediction of taxi service demand at specific temporal

and spatial junctures. Traditional forecasting

methodologies have demonstrated efficacy in the

analysis of linear time series data but have

encountered limitations when confronted with the

intricacies of nonlinear relationships and the

amalgamation of multi-source datasets. The incursion

of machine learning into this domain has heralded a

new epoch of forecasting approaches. For instance,

Guo et al. adeptly harnessed the Gradient Boosting

Decision Tree (GBDT) model to predict future taxi

demand trends with considerable success (Guo and

Chen, Z.

Machine Learning for Smart Cities: LSTM Model-Based Taxi OD Demand Forecasting in New York.

DOI: 10.5220/0013205400004568

In Proceedings of the 1st International Conference on E-commerce and Artiﬁcial Intelligence (ECAI 2024), pages 27-32

ISBN: 978-989-758-726-9

Shen, 2018). Similarly, Saadi et al. have integrated a

plethora of external factors (Saadi and Wang, 2017),

such as pricing and meteorological conditions, into

their predictive models, employing a diverse array of

algorithms including decision trees, ensemble

decision trees, and random forests. The foray of deep

learning into this realm has marked a significant leap

in forecasting capabilities due to their excellent

performance in many tasks (Lin, 2024; Wang, 2019).

Ke et al. have adeptly integrated deep learning with

machine learning techniques, employing Long Short-

Term Memory networks (LSTM) to encapsulate

temporal dependencies and Convolutional Neural

Networks (CNN) to model spatial correlations (Ke

and Zheng, 2017). Li has introduced Radial Basis

Function (RBF) neural network model, optimized via

quantum particle swarm optimization, which takes

into account an array of influencing factors such as

historical demand, traffic congestion indices, and

meteorological conditions (Li and Wen, 2018).

Despite these methodological advancements, the

ubiquitous challenge of reconciling supply and

demand in taxi services persists, adversely affecting

the operational efficiency of transportation systems

and the commuting experience of urban dwellers.

This paper aims to address this challenge by

conducting a comparative analysis of five distinct taxi

OD demand forecasting methodologies, utilizing data

analytics and machine learning algorithms, and

culminating in the identification of the LSTM model

as the most efficacious predictive instrument.

The rest of this paper is segmented into three

chapters, with the principal content of each chapter

delineated as follows: the method section details the

dataset and analytical methods; the results and

discussion section evaluate the performance of

Decision Tree (DT), LSTM, and random forest

models; and the conclusion reviews the research,

discusses limitations, and suggests future directions.

2 METHOD

2.1 Dataset Preparation

The dataset used in this study is sourced from the

Microsoft Azure Open Dataset. It encompasses a vast

collection of taxi trip records from 2009 to 2018,

totalling approximately 80 million entries

(TPSearchTool, 2022). Each entry is rich with details

such as precise latitude and longitude of pick-up and

drop-off locations, service dates and times, trip

distances, and fare amounts. The dataset's extensive

temporal and spatial coverage provides a

comprehensive view of taxi travel patterns in New

York City, offering valuable insights for urban

transportation planning and taxi service optimization.

The dataset includes several features such as Pickup

and Dropoff Latitude/Longitude, Passenger Count

and Payment Type.

The target variable for this study is the Taxi OD

demand, which is calculated by grouping data by start

and end points, demand date, and demand time, and

counting the number of orders from the same start

point to the same end point within the same hour.

This study also conducted a series of data

preprocessing steps on this dataset to ensure the

effectiveness of model training and the accuracy of

predictions. Initially, normalization was implemented

by applying the MinMaxScaler technique, which

scales the data to a range suitable for model training,

typically between 0 and 1. Following this, this paper

performed a train-test split, dividing the dataset into a

training set, which accounts for approximately 65%

of the total data, and a test set, comprising the

remaining 35%. This division is crucial for evaluating

the model's generalization capabilities. Additionally,

this study carried out data cleaning by filtering out

outliers based on geographical location and logical

inconsistencies within the data. For instance, records

with negative values for fare amount or passenger

count were identified and excluded to ensure the

quality and consistency of the dataset. Finally, to

reduce data dimensionality and facilitate model

training, K-Means clustering was employed. Using

this algorithm, this paper grouped the geographical

coordinates into seven distinct classes, streamlining

the data structure and enhancing the model's

efficiency in processing the information. This enables

model to predict Taxi OD demand more accurately

and provide robust data support for intelligent

transportation systems and urban planning.

The preprocessing steps were implemented using

Python, with libraries such as Pandas for data

manipulation, Scikit-learn for scaling and splitting the

dataset, and Matplotlib for visualization. Figures

illustrating the clustering results before and after

applying K-Means provide a visual representation of

the geographic distribution of taxi pick-up and drop-

off points. Figure 1 and Figure 2 below show the

location visualization after K-means clustering.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

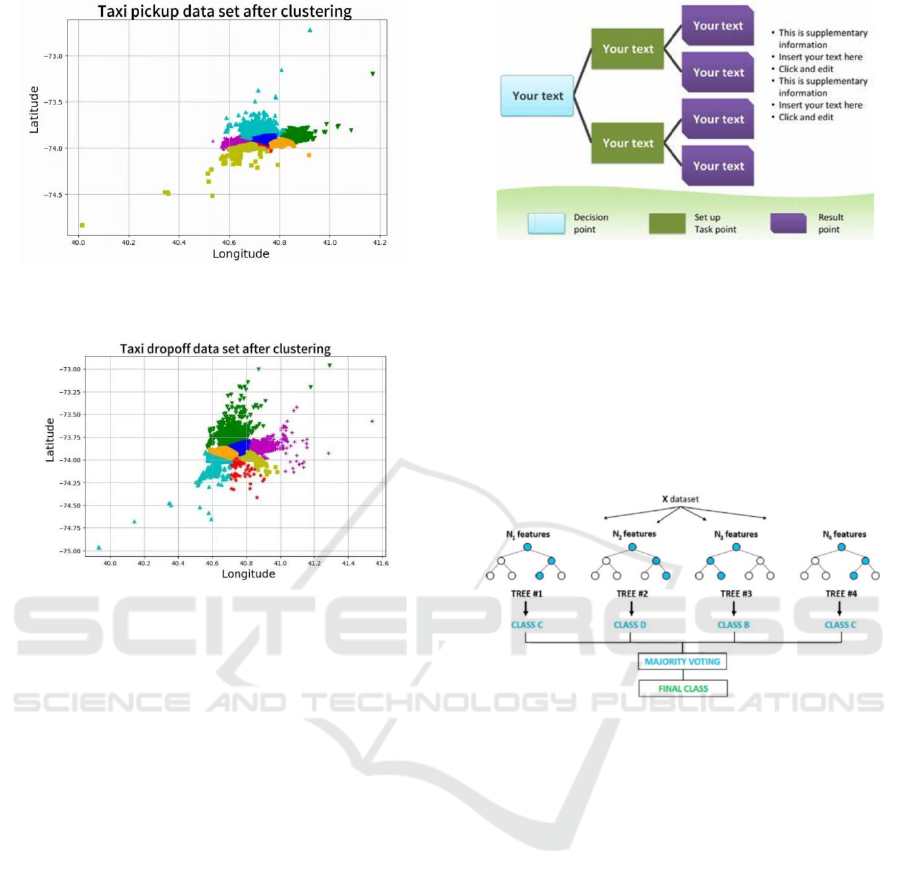
Figure 1: Distribution of taxi pick-up locations after

clustering (Photo/Picture credit : Original).

Figure 2: Distribution of taxi drop-off locations after

clustering (Photo/Picture credit : Original).

2.2 Machine Learning-based

Prediction

This study employed several machine learning

models to predict Taxi OD demand, including

Decision Trees, Random Forests, and Long Short-

Term Memory networks. The models were evaluated

using metrics such as Mean Squared Error (MSE),

Root Mean Squared Error (RMSE), and Mean

Absolute Error (MAE) to assess prediction accuracy

and generalization. The models were implemented

using popular machine learning libraries such as

Scikit-learn for DT and Random Forest (RF), and

TensorFlow for LSTM due to its capability to handle

complex neural network architectures.

Decision Trees shown in Figure 3 is an intuitive

and non-parametric supervised learning method used

for both classification and regression. It splits the

dataset into homogenous subsets recursively, creating

a tree-like model of decisions. The core principle of

DT is to partition the data space into regions that are

as pure as possible with respect to the target variable.

Figure 3: Schematic diagram of Decision tree

(TPSearchTool, 2022).

Random Forests shown in Figure 4 is an ensemble

learning method that constructs multiple DTs and

merges them to improve prediction accuracy and

control overfitting. RF reduces the variance of the

model by averaging the predictions of multiple trees,

each trained on a different subset of the data.

Figure 4: Schematic diagram of random forest algorithm

(Lee, 2020).

Long Short-term Memory network shown in

Figure 5 is a type of recurrent neural network (RNN)

capable of learning long-term dependencies. It is

particularly suited for time series prediction and tasks

requiring the memory of information over extended

periods. Critical LSTM hyperparameters

include units for the number of neurons in the LSTM

layer, batch_size for the number of samples per

gradient update, and epochs for the number of times

the training dataset is fed forward and backward

through the neural network.

Machine Learning for Smart Cities: LSTM Model-Based Taxi OD Demand Forecasting in New York

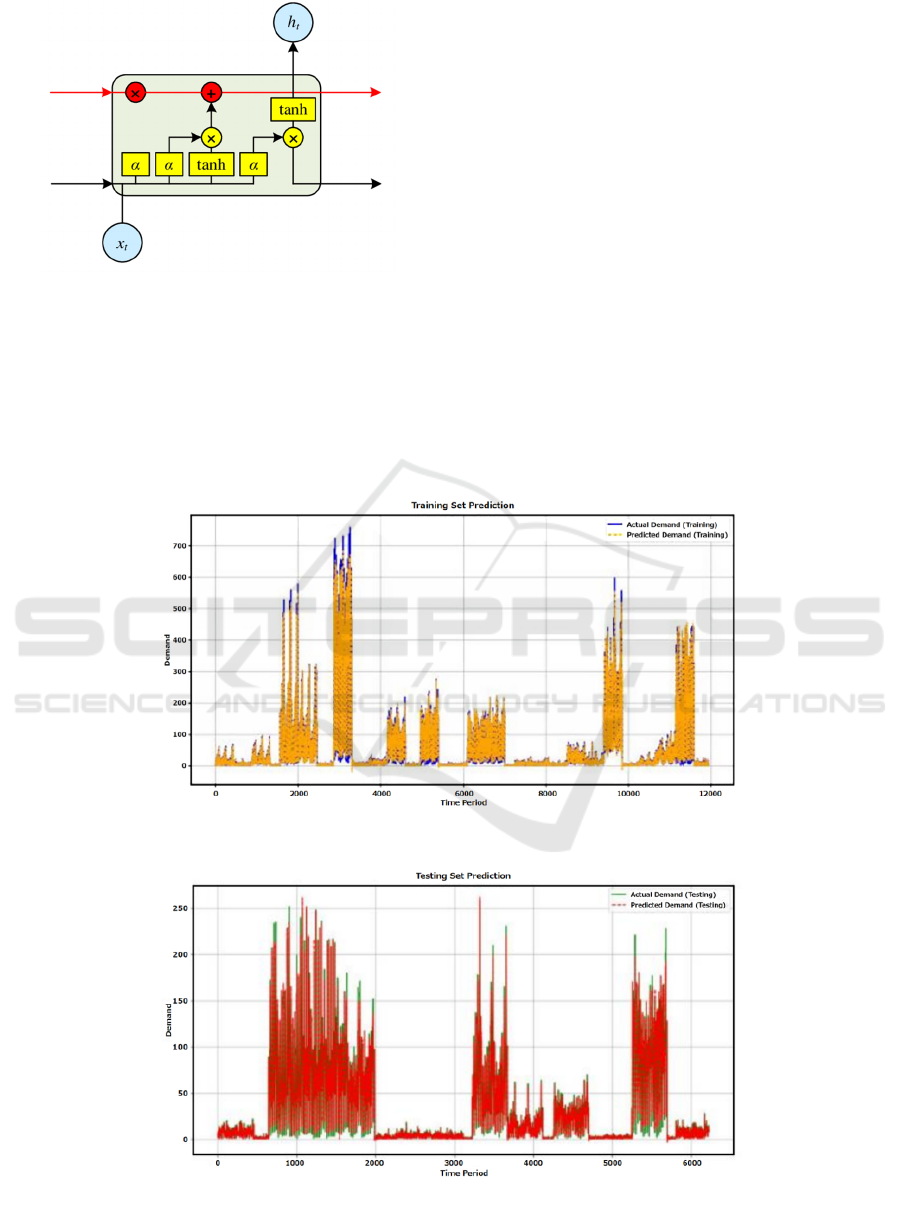
Figure 5: Schematic diagram of Long Short-term Memory

network (Wang, 2024).

The paper specifies a single LSTM layer in the

model architecture. The LSTM layer is configured

with four neurons, which are designed to capture the

long-term dependencies within the time series data.

LSTM layers use the hyperbolic tangent or a similar

function for the cell state activation. The output layer,

which is a Dense layer with a single output

dimension, likely uses a linear activation function

since this is a regression task. The model was

compiled using the MSE loss function, which is

standard for regression problems. The Adam

optimization algorithm was chosen for training the

LSTM model. Adam is known for its effectiveness in

handling different kinds of optimization problems

and is widely used due to its adaptive learning rate

properties. The model underwent 50 epochs of

iterative training. Each epoch processes the entire

dataset once.

Figure 6: Fitting effect of LSTM model on training set (Photo/Picture credit : Original).

Figure 7: Fitting effect of LSTM model on test set (Photo/Picture credit : Original).

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence

3 RESULTS AND DISCUSSION

The results of this study offer compelling insights into

the predictive capabilities of the LSTM model for

forecasting taxi OD demand in New York City. The

model's performance was rigorously evaluated

through a series of metrics, including MSE, RMSE,

and MAE. The LSTM model demonstrated

outstanding precision, with an MSE of 340.94, an

RMSE of 18.46, and an MAE of 9.46%. These results

were graphically represented in Figure 6 and Figure

7, which illustrate the model's fitting effects on both

the training and testing datasets, respectively.

The determination coefficient (R²) of the LSTM

model was calculated to be 0.9657, indicating that the

model accounts for approximately 96.57% of the

variance in taxi OD demand. This high R² value

underscores the model's proficiency in capturing the

complex spatiotemporal dynamics inherent in the

data. The LSTM model's superior performance over

the DT and RF models is evident when comparing the

evaluation metrics. The DT model reported an MSE

of 6857.76, an RMSE of 82.81, and an MAE of

50.67%, while the RF model showed an MSE of

6280.10, an RMSE of 79.25, and an MAE of 48.59%.

The LSTM model's significantly lower error metrics

suggest its enhanced ability to model the intricate

patterns of taxi demand.

The LSTM model's success can be attributed to its

architecture, which is adept at uncovering long-term

dependencies within the data. This is particularly

beneficial in the context of taxi demand forecasting,

where understanding patterns that extend over

extended periods is crucial. The model's ability to

learn from historical data and adapt to the temporal

dynamics of demand is a key factor in its predictive

accuracy. The discussion for drawbacks of decision

tree and random forest.

In optimizing the LSTM model, adjustments to

the hyperparameters, such as the sliding window size

and the number of iterations, were made. The first

optimization increased the number of iterations to

100, resulting in a stable model loss and no significant

changes in performance metrics. The second

optimization adjusted the sliding window to 450,

leading to a slight decrease in MSE, RMSE, and

MAE, and a final model loss of 6.1441e-04. These

adjustments highlight the model's sensitivity to its

configuration and the potential for further refinement.

Table 1 shows the complete results.

Table 1: OD demand prediction results of different models.

Method MSE RMSE MAE

DT 357.76 19.81 13.63

RF 373.52 26.25 7.43

LSTM 340.94 18.46 9.46

While this study focuses on the application of the

LSTM model to taxi OD demand in New York City,

it is worth noting the broader context of demand

forecasting research. Traditional methods, such as

time series analysis, have been eclipsed by machine

learning approaches, which offer more nuanced

predictions. The LSTM model's performance in this

study aligns with the growing body of literature that

supports the use of deep learning for time series

forecasting, particularly in the transportation sector.

The LSTM model is superior to RF and DT, possibly

because LSTM, as a deep learning model, is able to

capture long-term dependencies in time series data,

with which OD demand prediction is often correlated.

This ability of the LSTM model may allow it to more

accurately capture trends in the data when making

predictions, thus performing better on the average

absolute error. If there are large outliers in the

prediction error, MSE and RMSE will be greatly

affected because they calculate the square or square

root of the error. The sensitivity of MAE to outliers is

low. Also, LSTM may overfit during training, which

will also result in lower performance on the test set

than RF and DT.

The findings of this study lead to the conclusion

that the LSTM model is a robust tool for predicting

taxi OD demand. Its high R² value and low error

metrics indicate a strong correlation between the

model's predictions and actual demand patterns. The

model's ability to generalize, as evidenced by its

performance on the test dataset, suggests that it can

be effectively applied to other cities and traffic

scenarios with potential adjustments.

Future research should consider expanding the

LSTM model's application to diverse urban

environments and integrating real-time data streams

for enhanced predictive power. Additionally,

exploring the model's performance in a multi-modal

transportation context could provide a more

comprehensive understanding of urban mobility

patterns. The integration of real-time data sources,

such as traffic flow monitoring, weather changes, and

major events, could further enhance the model's

adaptability and accuracy in dynamic traffic

conditions. Moreover, the potential for combining the

LSTM model with other machine learning algorithms

to create hybrid models should not be overlooked.

Machine Learning for Smart Cities: LSTM Model-Based Taxi OD Demand Forecasting in New York

Such hybrid models could leverage the strengths of

multiple algorithms to improve predictive

performance. The exploration of these avenues could

pave the way for more sophisticated and accurate

demand forecasting tools that can support smarter

urban transportation planning and management.

4 CONCLUSIONS

In conclusion, this study effectively harnesses the

power of the LSTM model to predict the Origin-

Destination demand for taxis in New York City,

presenting a notable contribution to the field of urban

transportation planning. The primary methodology

used in this study encompasses the utilization of

sophisticated data analytics techniques and machine

learning algorithms, culminating in the development

of an LSTM model that surpasses other models in

terms of predictive accuracy and generalization

capability. The results not only validate the LSTM

model's superior predictive prowess but also highlight

its ability to capture intricate demand patterns, as

evidenced by a high R² of 0.9657.

While the study has made significant strides, it

also acknowledges the limitations that accompany

such an advanced model. Among these is the model's

sensitivity to hyperparameter tuning, which can be a

complex process requiring extensive computational

resources and expertise. Additionally, the model's

performance is contingent upon access to large

volumes of high-quality historical data, which may

not always be readily available or up-to-date. In the

future, efforts will be directed towards improving the

model's generalizability, enabling it to perform

effectively across a variety of urban settings with

diverse traffic patterns and characteristics. This will

involve testing the model in different cities and under

various traffic conditions to ensure its predictions

remain reliable and accurate.

REFERENCES

Guo, X., & Shen, Y. 2018. Demand prediction of e-taxi

based on gradient lifting regression tree [In Chinese]. In

Proceedings of the 2018 World Transport Congress (pp.

310-320). Beijing, China.

Ke, J., Zheng, H., Yang, H., et al. 2017. Short-term

forecasting of passenger demand under on-demand ride

services: A spatio-temporal deep learning approach.

Transportation Research Part C: Emerging

Technologies, 85, 591-608.

Lee, K., Claridades, A. R. C., & Lee, J. 2020. Improving a

street-based geocoding algorithm using machine

learning techniques. Applied Sciences, 10(16), 5628.

Li, J., Wen, H., Lin, L., et al. 2018. Prediction model of car-

hailing demand based on QPSO_RBF Neural Network

[In Chinese]. Journal of Guangxi University (Natural

Science Edition), 43(2), 272-281.

Lin, Z., Zhu, G., Deng, Y., Chen, X., Gao, Y., Huang, K.,

& Fang, Y. 2024. Efficient parallel split learning over

resource-constrained wireless edge networks. IEEE

Transactions on Mobile Computing.

New York City Government. 2017. New York City

Mobility Report.

Saadi, I., Wong, M., Farooq, B., et al. 2017. An

investigation into machine learning approaches for

forecasting spatio-temporal demand in ride-hailing

service. arXiv preprint arXiv:1703.02433.

TPSearchTool. 2022. How to make a decision tree in Excel:

A free template decision tree images. Retrieved August

7, 2024, from https://www.tpsearchtool.com/

images/how-to-make-a-decision-tree-in-excel-a-free-

template-decision-tree

Wang, F., Casalino, L. P., & Khullar, D. 2019. Deep

learning in medicine—promise, progress, and

challenges. JAMA internal medicine, 179(3), 293-294.

Wang, J. 2024. Study on the influencing factors of the

development of art education in colleges and

universities based on the deep learning model. Applied

Mathematics and Nonlinear Sciences.

ECAI 2024 - International Conference on E-commerce and Artiﬁcial Intelligence