
Optimizing Credit Card Fraud Detection with Multi-Armed
Bandit Algorithms
Rongjun Gao
The University of Michigan-Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University,
No. 800, Dongchuan Road, Minhang District, Shanghai, China
Keywords: Credit Card Fraud Detection, UCB1, Thompson Sampling.
Abstract: In today's world, the importance of credit card fraud detection cannot be overstated, as it is crucial for the
security of financial transactions. To optimize cost-efficiency, automated algorithms have been developed to
pinpoint the transactions that are most likely to be fraudulent. Despite their potential, multi-armed bandit
(MAB) algorithms have not been widely adopted in fraud detection. This paper introduces two models that
apply the Upper Confidence Bound 1 and Thompson sampling algorithms to the task of fraud detection,
categorizing transactions into 52 segments based on the amount and type. The performance of these
algorithms is evaluated against several metrics, including cumulative regret, the reward generated, the ratio
of optimal arm selection, and overall efficiency. The findings suggest that the Thompson sampling algorithm
surpasses the UCB1 in performance, achieving lower standard errors and computational complexity. It proves
to be more effective in swiftly and accurately identifying the most suspicious transactions, thus pinpointing
the optimal choice with greater speed.
1 INTRODUCTION
In modern society, credit cards are widely used for
transactions for its convenience and simplicity.
However, this also provides opportunities for fraud
cases to happen due to the swiftly changing essence
of financial services together with potential monetary
interest (Ferreira and Meidutė-Kavaliauskienė,
2019). Credit card transaction frauds happen
frequently and can easily trigger huge property losses
for both individuals and corporations without early
detection. Therefore, fraud has drawn wide attention
in areas such as business and commerce (Bernard et
al., 2019). Financial institutions are also confronting
high risks and uncertainties caused by these losses
(Sariannidis et al., 2019). On the other hand, human
experts can only examine a limited number of credit
card transactions in a fixed period of time (e.g. 1000
every month) (Soemers et al., 2018). Therefore,
there’s an urgent need for a model that can identify
transactions with the highest probability of being
fraudulent.
Typically, pre-trained machine learning models
are used for fraud detection. Existing models and
algorithms used for detecting potential frauds consist
of the following types. In Logistic Regression, the
sigmoid function is mainly applied to predict and
judge the probability of a transaction being
fraudulent. The transaction is considered suspicious if
the sigmoid output value is over 0.5 and legitimate
otherwise (Awoyemi et al., 2017). Together with
modified gradient ascent optimization, the classifier
updates new data gradually instead of all at once to
calculate the best-fit parameters (Awoyemi et al.,
2017). In Naïve Bayes, prior samples and conditional
probabilities are taken advantage of to make decisions
with the highest Bayesian probability (Awoyemi et
al., 2017). Grounded on the Bayesian classification
rule, the binary classification of fraudulent
transactions and legitimate transactions is performed
with the assumption that all data features are
conditionally independent (Awoyemi et al., 2017). In
the K-Nearest Neighbours algorithm (KNN),
traditional distance functions such as the Euclidean
distance and Minkowski distance are applied to
classify K data points with the lowest distances into
one group (Awoyemi et al., 2017). KNN exhibits the
best performance among the three algorithms based
on standards such as classification accuracy, balanced
rate, Matthews correlation coefficient (MCC)
(Awoyemi et al., 2017), etc., but also demonstrates
drawbacks including a requirement for sufficient
474
Gao, R.
Optimizing Credit Card Fraud Detection with Multi-Armed Bandit Algorithms.
DOI: 10.5220/0012956000004508
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Engineering Management, Information Technology and Intelligence (EMITI 2024), pages 474-478
ISBN: 978-989-758-713-9
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

samples, overfitting, weak generalization, and
computational complexity (Zhang, 2022). On the
other hand, multi-armed bandit (MAB) algorithms are
seldom applied to credit card fraud detection due to
difficulties in forming suitable arms based on
excessively imbalanced data. In addition, fraudsters
are always finding a way to cheat detection models by
making fraud appear legitimate, which is known as
the concept drift (Dornadula and Geetha, 2019). In
this sense, properly tackling concept drift for non-
stationary data streams becomes a challenge
(Soemers et al., 2018).
This paper seeks to apply traditional MAB
algorithms including the UCB1 and Thompson
sampling algorithms to construct two fraud detection
models and examines the effect of the models in terms
of the cumulative regret after 100,000 rounds. All
codes are implemented in Python 3.11.4. The dataset
used in this article records real credit card
transactions over the globe. The arms are constructed
based on 4 transaction amount intervals and 13
transaction types. The reward is given to the model
whenever the model successfully identifies a fraud,
and an evaluation standard called cumulative regret is
defined as the gap between the maximum reward and
the actual obtained reward. A comparative analysis of
the performance of the UCB1 and Thompson
sampling algorithm is given in this paper, particularly
focusing on the evaluation of cumulative regret,
generated reward, optimal arm selection ratio, and
algorithm efficiency. The results show that the
Thompson sampling algorithm exhibits superior
performance than the UCB1 algorithm.
The rest of paper is organized as follows: Section
2 describes the detailed parameters of the dataset used,
the arm classification standard, and the definition of
regret, and introduces the UCB1 and Thompson
sampling algorithms. Section 3 compares the
performance of the UCB1 and Thompson sampling
algorithms in terms of cumulative regret, optimal arm
selection ratio, etc. Section 4 makes a conclusion of
this comparative study, states the future areas for
research, and provides some suggestions.
2 METHOD
2.1 Dataset
The dataset used in this article includes real credit
card transaction records from June to December in
2020 over the globe with 555719 instances. 22
attributes are exhibited in the dataset (transaction
date, transaction amount, customer identification
number, etc.), and 2 attributes (transaction amount
and transaction category) are chosen as the standard
of classification of multiple arms. The transaction
amount ranges from $1.00 to $22768.11, and the
transaction category includes 14 transaction types
(“personal care”, “health fitness”, etc.). There are
2145 fraudulent transactions in this dataset in total.
Notably, the dataset displays significant skewness,
where 99% of transaction amount lies in the interval
$1.00~$519.85, and only 1% lies in
$519.85~$22768.11. The overview of the dataset is
listed in Table 1.
Table 1: Dataset overview.
Total
dataset
Fraud Not fraud Label not
frau
d
Label
frau
d
555719 553574 2145 0 1
2.2 Arm Classification Standard and
Regret Definition
Among the 22 attributes of the dataset, the transaction
amount and the transaction category are applied for
the classification of arms. The transactions are
divided into four parts based on the transaction
amount so that the number of people falling into each
part accounts for a quarter of the total number of
people. As previously stated, the transaction category
includes 14 transaction types. For the sake of
convenience, the "grocery point of sale” type and the
“grocery net” type are combined into one type called
“grocery”. From these two dimensions, all
transactions can be classified into 52 types (4×13),
and each represents one arm in the MAB model.
The set of all arms is denoted by 𝒜, the horizon
is denoted by
n
, and each individual arm are labeled
i , where
1,...,52i =
. An arbitrary round is denoted
by
t
. The total number of transactions in each arm is
denoted by
i
s
, and the transaction amount of one
particular transaction is
,ip
s
, where i represents
which arm this transaction belongs to, and
p
represents it’s the pth transaction of this arm (
1
i
p
s≤≤
). The mean transaction amount of each arm
is given by
,
1
1
i
s
i
ik
k
i
ms
s
=
=
(1)
and the total mean reward of each arm is
,
,
1
1
i
iik
s
ik
k
i
rbs
s
=
=
(2)
Optimizing Credit Card Fraud Detection with Multi-Armed Bandit Algorithms
475

where
,
1
ip
b =
if the 𝑝th transaction of arm i is a
fraud, and
,
0
ip
b =
if otherwise. The general
assumption of this model is that the optimal arm is
unique (denoted by
* ) for simplicity, and its mean
reward
*1252
max{ , ,..., }rrrr=
. The actual random
reward in round 𝑡 is defined as
()
,,
if the th transaction of arm is
ˆ
picked
0otherwise
ip ip
i
i
sb
pi
xt
m
=
and the actual mean reward of arm 𝑖 until round 𝑡 is
given by
𝑟
̂
𝑡
=
∑
𝑥
𝑘
(3)
where 𝑧
𝑡
denotes the times arm
i has been played
until round
t
. The total regret until round
t
is
defined as
()
52
1
ˆ
ti
i
Rrt
=
=
(4)
and the goal of this article is to minimize the total
regret so that the model can identify as many
fraudulent cases as possible within its horizon.
2.3 UCB1 Algorithm
In UCB1, the UCB index for an arm i in round t is
defined as
() ()
()
ln
ˆ
2()
ii
i
n
B
UCB t r t
zt
α
=+
(5)
where
B
represents the gap between the maximum
and minimum reward value, and λ is a parameter. The
algorithm will initially pull each arm once to calculate
the initial UCB indices for all arms. Subsequently, in
every round, the algorithm selects the arm with the
highest UCB index to pull. Then in every upcoming
round, the algorithm will pick the arm with the largest
UCB index. In this way, the algorithm successfully
applies the principle of optimism and takes the
strategy that each arm is considered to give higher
rewards than they did in the past (Tor and Szepesvári,
2020). The gap-dependent regret upper bound is
𝑂
Δ
, and the gap-independent regret upper
bound is
()
()
Oln
K
nn
, where 52K = in this
article,
*ii
rrΔ= −
, Δ =min Δ
Δ
>0
(Mukherjee
et al., 2018).
Algorithm 1: UCB1 (Tor and Szepesvári, 2020).
Input: Time horizon
n
, reward value gap
B
Pull each arm once
for
53,...,tn=
do
Pull arm
()
152
argmax UCB 1
jj
it
≤≤
=−
Reset parameters:
() ( )
:11
ii
zt zt=−+
𝑟̂
𝑡
:=
∑
𝑥
𝑘
𝑈𝐶𝐵
𝑡
:=𝑟
̂
𝑡
+
α
()
2.4 Thompson Sampling Algorithm
In Thompson Sampling algorithm, the model will
pick the arm based on randomization and Bayesian
analysis (Tor and Szepesvári, 2020). The algorithm
will first pull each arm once, and then assign each arm
a posterior
𝑁𝑟̂
(
𝑡−1
)
,
()
. In each
upcoming round, the algorithm will first sample
𝑣
~𝑁𝑟̂
(
𝑡−1
)
,
()
from the posterior of
each arm, and then pick arm
152
argmax
j
j
iv
≤≤
=
.
Finally, the algorithm will update each arm’s
posterior according to the obtained reward. Based on
the utilization of posteriors and the random arm-
picking process, the algorithm is endowed with the
ability to explore suboptimal arms while also
exploiting the optimal arm as much as possible. The
regret of this algorithm is proved to be
𝑂
∑
Δ
𝑙𝑛
(
𝑛
)
Δ
when the actual probability
distribution of each arm is Gaussian (Tor and
Szepesvári, 2020).
A
lgorithm 2: Thompson sampling algorithm (Tor an
d
Szepesvári, 2020).
Input: Time horizon
n
, reward value gap
B
Pull each arm once
for
53,...,tn=
do
for
1,...,52i =
do
Sample
𝑣
~𝑁
𝑟̂
(
𝑡−1
)
,
()
Pull arm
152
argmax
j
j
iv
≤≤
=
Reset parameters:
() ( )
:11
ii
zt zt=−+
𝑟̂
(
𝑡
)
:=
(
)
∑
𝑥
(
𝑘
)
Update the posterior
𝑁
𝑟
̂
(
𝑡
)
,
()
EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence
476
3 RESULTS
3.1 UCB1 Algorithm Performance
The model parameter
α
and the horizon
n
are
chosen to be 1 and 100000, respectively. The result is
averaged over 100 random experiments. As shown in
Table 2, among 100000 rounds, the optimal arm is
picked 96971.49 times on average, far more than
3028.51 times of picking all other arms. The reward
generated by the optimal arm is 96971.23, which
significantly outperforms the total reward generated
by other arms (37.84 on average).
Table 2: UCB1 algorithm performance overview.
Count of
selection
Percentage
count
Reward
generate
d
Optimal arm 96971.49 96.97% 96971.23
Other arms
3028.51
3.03%
37.84
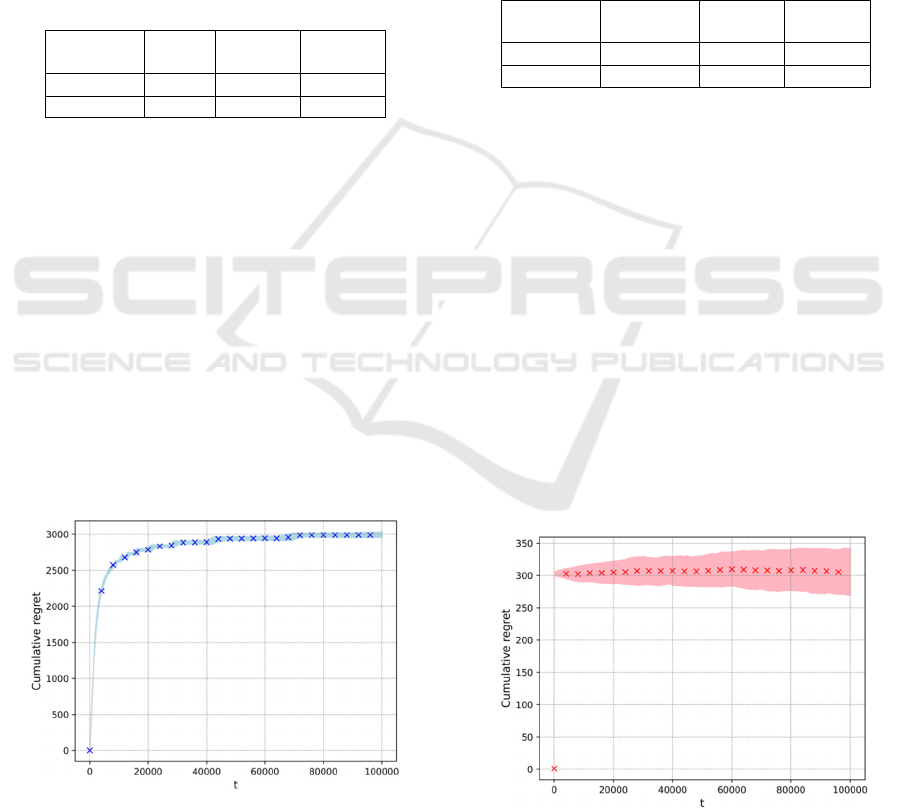
Figure 1 visualizes the overall performance of the
UCB1 algorithm. The average cumulative regret is
marked every 4000 rounds using blue crosses, and
one standard error is marked in light blue. As
demonstrated in Fig. 1, the average cumulative regret
increases logarithmically with the round growing. A
significant amount of loss from failing to choose the
optimal arm is suffered in the initial stage, and less
loss is produced after the exploration stage, leading to
the increasing accuracy of identifying potential credit
card frauds. The average regret after 100000 rounds
is 2990.93 with a relatively small standard error of
38.84, which proves the stability of the UCB1
algorithm. The running time of this algorithm is
135.65 seconds, proving the efficiency of this
algorithm.
Figure 1: Cumulative regret using UCB1 algorithm with
1α=
.
3.2 Thompson Sampling Algorithm
Performance
The horizon
n
is chosen to be 1 and the result is
averaged over 100 random experiments. As shown in
Table 3, among 100000 rounds, the optimal arm is
picked 99693.94 times on average, which indicates
the model picks the optimal arm more than 99% of
total times. The reward generated by the optimal arm
is 99690.99, a sharp comparison with the total reward
from all other arms (272.83 on average).
Table 3: Thompson sampling algorithm performance
overview.
Count of
selection
Percentage
count
Reward
generate
d
Optimal arm
99693.94 99.69% 99690.99
Other arms 306.06 0.31% 272.83
As displayed in Figure 2, the cumulative mean
regret every 4000 rounds is marked using red crosses,
while the standard error of each round is plotted in
light pink. In comparison with the UCB1 algorithm,
the total regret of the Thompson sampling algorithm
after 100000 rounds is 305.89, far less than 2990.93
of the UCB1 algorithm. On the other hand, the regret
skyrockets in approximately the first 1000 rounds and
then increases at an extremely slow speed, which
indicates the variance of the posterior of the optimal
arm has converged to zero and the model has
successfully identified the optimal arm. In large, the
cumulative regret curve does not present a
logarithmic shape. The standard error is 36.17, nearly
the same as the one of the UCB1 algorithm (38.84).
The running time of the Thompson sampling
algorithm is 120.50 seconds, which is even fewer than
the one from the UCB1 algorithm (135.65 seconds).
Figure 2: Cumulative regret using Thompson sampling.
Optimizing Credit Card Fraud Detection with Multi-Armed Bandit Algorithms
477

4 CONCLUSIONS
This study explores the application of multi-armed
bandit (MAB) algorithms, including UCB1 and
Thompson Sampling, to the problem of credit card
fraud detection. Transactions are categorized into 52
distinct groups, or 'arms,' based on their types and
amounts. The goal of these models is to pinpoint the
arm with the highest likelihood of fraudulent activity,
thereby directing human investigators to the most
suspect transactions within a vast dataset. The
approach is validated by its performance in
minimizing cumulative regret, which enables
financial institutions to efficiently focus on arms
yielding the highest average reward. Furthermore, the
Thompson Sampling algorithm demonstrates
superior performance over the UCB1 algorithm by
achieving lower cumulative regret, exhibiting small
standard errors akin to those of UCB1, and
maintaining low computational complexity. For
future work, the arms can be formed more reasonably
and comprehensively. In this paper, merely
transaction types and transaction amounts are taken
into account. More features of these transactions can
be utilized since the dataset provides additional 20
unused attributes with advanced algorithms including
the incremental Regressions Trees, KNN, etc., to
cluster different transactions into multiple arms. On
the other hand, it’s claimed that fraudsters will
constantly modify their behaviors in order to escape
detection from existing models, known as concept
drift (Soemers et al., 2018). In this sense, the methods
of clustering different transactions into arms should
also take concept drift into consideration and be
updated regularly. Furthermore, more MAB
algorithms such as LinUCB, Efficient-UCBV,
Discounted UCB and Sliding window UCB (Garivier
and Moulines, 2008) can be implemented and tested
so that the computational complexity and cumulative
regret can be further reduced, or the concept drift may
be better handled.
REFERENCES
Lattimore, T., Szepesvári, C., 2020. Bandit Algorithms.
Cambridge University Press.
Mukherjee, S., Naveen, K. P., Nandan, S., Balaraman, R.,
2018. Efficient-UCBV: An almost optimal algorithm
using variance estimates. Proceedings of the AAAI
Conference on Artificial Intelligence.
Soemers, D., Brys, T., Driessens, K., Winands, M., Nowé,
A., 2018. Adapting to concept drift in credit card
transaction data streams using contextual bandits and
decision trees. Proceedings of the AAAI Conference on
Artificial Intelligence.
Awoyemi, J., Adetunmbi, A., and Oluwadare S., 207.
Credit card fraud detection using Machine Learning
Techniques: A Comparative Analysis. 2017
International Conf. on Computing Networking and
Informatics (ICCNI).
Garivier, A., Moulines, E., 2008. On upper-confidence
bound policies for non-stationary bandit problems.
Bernard P., El Mekkaoui De Freitas N., Maillet B., 2019. A
financial fraud detection indicator for investors: An
IDeA. Annals of Operations Research.
Ferreira, F., Meidutė-Kavaliauskienė, I., 2019. Toward a
sustainable supply chain for Social Credit: Learning by
experience using single-valued neutrosophic sets and
fuzzy cognitive maps. Annals of Operations Research.
Sariannidis, N., Papadakis, S., Garefalakis A., Lemonakis
C., Kyriaki-Argyro T., 2019. Default avoidance on
credit card portfolios using accounting,
Demographical and exploratory factors: Decision
making based on machine learning (ML) techniques.
Annals of Operations Research.
Zhang, S., 2022. Challenges in KNN classification. IEEE
Transactions on Knowledge and Data Engineering.
Dornadula, V., Geetha, S., 2019. Credit card fraud
detection using machine learning algorithms. Procedia
Computer Science.
EMITI 2024 - International Conference on Engineering Management, Information Technology and Intelligence
478
