A Parameter-Free Self-Training Algorithm for Dual Choice Strategy
Wei Zhao, Qingsheng Shang
*
, Jikui Wang, Xiran Li, Xueyan Huang and Cuihong Zhang
College of Information Engineering and Artificial Intelligence,
Lanzhou University of Finance and Economics, Lanzhou 730020, Gansu, China
Keywords: Self-Training, High-Confidence Samples, Dual Choice Strategy.
Abstract: In the field of machine learning, semi-supervised learning has become a research hotspot. Self-training
algorithms, improve classification performance by iteratively adding selected high-confidence samples to the
labeled sample set. However, existing methods often rely on parameter tuning for selecting high-confidence
samples and fail to fully account for local neighborhood information and the information of labeled samples.
To address these issues, this paper proposes a self-training algorithm with a parameter-free self-training
algorithm for dual choice strategy. Firstly, the selection problem of K-value in KNN classifier is solved by
using natural neighbors to capture the local information of each sample, and secondly, adaptive stable labels
are defined to consider the information of labeled samples. On this basis, a decision tree classifier is introduced
to combine the global information for double selection to further select high-confidence samples. We
conducted experiments on 12 benchmark datasets and compared them with several self-training algorithms.
The experimental results show that the FSTDC algorithm achieves significant improvement in classification
accuracy.
1 INTRODUCTION
In the field of semi-supervised learning (SSL)(Van
Engelen and Hoos, 2020), self-training algorithms
play a crucial role, which aiming to improve the
performance of classifiers by combining a small
amount of labeled data with a large amount of
unlabeled data. Li et al (Li et al., 2005) proposed the
self-training with editing algorithm(SETRED), which
uses data editing techniques to identify and reject
potentially mislabeled samples from the labeling
process. Despite the progress SETRED has made in
improving the robustness of self-training, it relies on
manually set thresholds. To overcome this limitation,
Wu et al (Wu et al., 2018) proposed the self-training
semi-supervised classification based on density peaks
of data algorithm(STDP), which is based on the
concept of density peak clustering (DPC)(Rodriguez
and Laio, 2014) and is able to reveal the underlying
data on data distributions of different shapes. The
STDP algorithm does not rely on specific data
distribution assumptions, thus expanding the
application scope of self-training algorithms. Zhao et
al(Zhao and Li, 2021) introduced the concept of
natural neighbors based on STDP and proposed a
semi-supervised self-training method based on
density peaks and natural neighbors algorithm
(STDPNaN). Furthermore, Li et al
(Li et al., 2019)
proposed a self-training method based on density
peaks and an extended parameter-free local noise
filter for k nearest neighbor (STDPNF). An extended
parameter-free local noise filter (ENaNE) was
proposed to address the problem of mislabeled
samples in STDP. The design of ENaNE cleverly
exploits the information of both labeled and unlabeled
data, and efficiently filters noise. Wang et al(Wang et
al., 2023) proposed a self-training algorithm based on
the two-stage data editing method with mass-based
dissimilarity (STDEMB) based on the previous work.
The STDEMB algorithm, through a prototype tree
design, which effectively edits mislabeled samples
and selects high-confidence samples during self-
training.
Based on the above algorithms, a parameter-free
self-training algorithm for the dual selection strategy
is designed. It is not only parameter-free, but also
integrates the global and local information of the
samples, while making full use of the information of
the labeled samples. In addition, a decision tree
classifier is introduced for high-confidence sample
selection, which is extensively experimentally
validated on several datasets, proving its
102
Zhao, W., Shang, Q., Wang, J., Li, X., Huang, X. and Zhang, C.
A Parameter-Free Self-Training Algorithm for Dual Choice Strategy.
DOI: 10.5220/0012920900004536
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Data Mining, E-Learning, and Information Systems (DMEIS 2024), pages 102-107
ISBN: 978-989-758-715-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

effectiveness and superiority in SSL tasks.
2 RELATED WORK
2.1 Relevant Symbol
{
}
1
,...,
n
X
xx=
denotes a dataset containing
n
samples.
𝑌 =

𝑦

,...,𝑦


represents the set of labels.
𝐿 ={(𝑥

, 𝑦

),...,(𝑥

, 𝑦

)} denotes a labeled
sample
set containing
𝑙
labeled samples.
𝑈 =
{
𝑢

,...,𝑢

}
denotes the set of unlabeled
samples, which contains
nl− unlabeled samples.
2.2 Self-Training Algorithm
The self-training algorithm is a semi-supervised
learning strategy that iteratively improves the
performance of a classification model by
progressively integrating the high-confidence
samples. The algorithm first trains an initial model on
a limited amount of labeled data, and then the model
generates pseudo-labels by predicting a large amount
of unlabeled data. The most reliable part of them is
selected to be added to the training set. Its general
process is shown in the table below.
2.3 Comparison Algorithm
2.3.1 STDP
STDP uses density peaks in the data space to discover
the structure of the data. It then integrates structural
information into the self-training process by
alternately selecting the ‘previous’ and ‘next’
unlabeled samples of a labeled sample and adding
these samples and their predicted labels to the training
set. This process is iterated until a more accurate
classifier has been trained.
2.3.2 SETRED
The SETRED algorithm introduces data processing
techniques. The algorithm captures the local structure
of the data by constructing a neighborhood graph and
uses a local cut edge weight statistic (CEW) to
identify and exclude potentially mislabeled samples.
The SETRED algorithm improves the generalization
of the model by adding only those samples to the
training set in each iteration that have passed the
reliability test.
2.3.3 STDPNaN
Classification performance is improved by
combining the concept of density peaks and natural
neighbors. The algorithm first reveals the true
structure and distribution of the data using improved
density peak clustering without parameters
(DPCNaN), and then continuously adds unlabeled
samples with high confidence to the training set
through self-training process, where an integrated
classifier is used to improve the prediction capability.
2.3.4 STDEMB
The STDEMB algorithm is based on a two-stage data
editing approach and mass-based dissimilarity to
improve the performance of semi-supervised learning.
It develops an innovative two-stage data editing
strategy that effectively selects unlabeled samples
with high confidence and explores the relationship
between unlabeled samples and labeled samples
through a prototype tree.
Algorithm 1: Self-training algorithm.
Input：
L
,
U
Output：Classifier
C
1.Initialise high confidence sample set
S =∅
2.While
U ≠∅
DO
3. Train the classifier C using the labeled sample set
L
4. Assigning labels to unlabeled sample set
U
using classifier
C
5. Select the high-confidence sample set
S
from
U
6.
,LLSUUS←∪ ← −
7.End While
A Parameter-Free Self-Training Algorithm for Dual Choice Strategy
103

3 OUR ALGORITHM
3.1 Definitions
Definition1(Natural Neighbors)
In the field of data science, the concept of natural
neighbors is a mathematical abstraction of the mutual
recognition relationship in social network theory. The
core of this concept lies in the fact that the
neighborhood relationship between data points is
mutual, i.e., one data point and another data point are
each other's nearest neighbors at the same time.
Natural neighbors do not require predefined
parameters and are defined as follows:
()
{
}
(), ( )
ijj ii j
NN x x x KNN x x KNN x=∈ ∈
(1)
where 𝐾𝑁𝑁(𝑥

) denotes the nearest neighbors
and 𝑁𝑁(𝑥

) denotes the set of natural neighbors.
Definition 2(Natural Stabilization Structure)
The natural stable structure is a special type of data
form in which every data point in a dataset forms a
natural neighbor relationship with at least one other
data point. The existence of such a structure implies
that the dataset exhibits an intrinsic stability in which
the data points are connected to each other through
mutually recognized neighbor relationships,
constituting a stable structure known as the natural
stable structure. For any data point
i
x
, there exists at
least one that satisfies the following relationship:
() (),
ijjiij
x
NN x x NN x x x∈∪∈ ≠
(2)
Definition 3(Natural Neighbor Label Set)
The natural neighbor label set represents the set of
labels of the natural neighbors of a sample.
𝑦

(𝑥

)=𝑦

𝑥

∈𝑁𝑁(𝑥

) (3)
where
𝑦

(𝑥

)
denotes the set of natural
neighborhood labels for sample
𝑥

.
Definition 4(Adaptive Stable Labels)
Adaptively stable labels denote the class of labels
with the highest number of occurrences in the set of
natural neighborhood labels, which is represented as
follows:
() ( ())
AS i NN i
y
xModeyx=
(4)
Where 𝑦

(𝑥

) denotes the adaptive stable label of
sample
i
x
and 𝑀𝑜𝑑𝑒(•) is the function used to
calculate the number of plurality in a set.
3.2 Description of the Algorithm
In order to fully consider the domain information of
the samples and the information of the labeled
samples, we designed the FSTDC algorithm. Firstly,
it does not require preset parameters and is based on
natural neighborhood adaptive learning. Secondly, it
adopts a dual selection strategy based on decision tree
classifier, which selects as high-confidence samples
when and only when the adaptively stable labels and
the predicted labels of the decision tree classifier
match, which improves the quality of the selected
high-confidence samples. The process of
FSTDC
algorithm is shown in the following table.
4 EXPERIMENTS
The experimental sessions of this study were
executed in the same configuration of the computing
environment, which consisted of a 64-bit Windows 10
operating system, 64 GB RAM, and an Intel Core i9
processor. The software environment used for the
experiments was MATLAB 2023a.
4.1 Description of the Data Set
To validate the performance of FSTDC, we selected
12 datasets from UCI, the details are shown below.
Table 1: datasets
details.
index dataset samples features classes
1 AR 1680 1024 120
2 Australian 690 14 2
3 Balance 625 4 3
4 BUPA 345 6 2
5 Cleve 303 13 8
6 crx_uni 690 15 2
7 Ecoli 336 7 8
8 FERET32x32 1400 1024 200
9 Glass 214 9 6
10 Haberman 306 3 2
11 ORL 400 1024 40
12 Yeast 1484 1470 10
DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems
104

Algorithm 2: FSTDC algorithm.
Input：
L
,
U
Output：Classifier
C
1.While true
2. Initializing KNN classifier using labeled samples
3. Initialize
S =∅
4. For each unlabeled sample 𝑥

in 𝑈
5. Natural neighbors 𝑁𝑁
(
𝑥

)
of
i
x
obtained through equation (1)
6. The set of natural neighborhood labels
𝑦

(𝑥

)
of
i
x
is obtained through equation (3)
7. Adaptive stabilization labels
()
AS i
y
x
obtained by equation (4) for
i
x
8. Assigning predictive labels
()
CART i
yx
to unlabeled samples
i
x
using decision tree classifiers
9. If
𝑦

(𝑥

)=𝑦

(𝑥

)
10. Add
i
x
to
S
11. End If
12. If
S =∅
13. Break
14. End If
15.
𝐿 = 𝐿∪𝑆, 𝑈 = 𝑈−𝑆
16.End While
17.Return
C
Table 2: The accuracy results of the algorithms.
Datasets STDP SETRED STDEMB STDPNaN FSTDC
AR 78.19±1.07(4) 78.44±1.23(3) 77.62±1.14(5) 84.67±1.23(2) 91.76±1.04(1)
Australian 64.15±3.43(5) 64.17±2.30(4) 67.87±2.86(2) 64.86±3.15(3) 68.92±2.39(1)
Balance 76.64±1.89(3) 77.12±2.15(2) 75.08±5.73(4) 74.71±2.21(5) 80.95±6.58(1)
BUPA 59.63±4.1(4) 60.2±3.18(2) 59.58±5.59(5) 59.84±4.08(3) 61.62±5.89(1)
Cleve 75.22±5.67(5) 76.12±5.61(4) 78.58±5.07(2) 78.2±4.77(3) 79.69±2.21(1)
crx_uni 63.68±2.92(4) 65.26±3.59(3) 67.96±3.43(2) 63.44±3.9(5) 69.25±2.8(1)
Ecoli 89.88±2.77(3) 88.84±3.53(5) 89.15±3.8(4) 90.94±2.1(2) 91.09±1.81(1)
FERET32x32 84.11±0.76(3) 83.88±0.73(4) 83.8±0.99(5) 88.53±1.5(2) 97.47±0.44(1)
Glass 76.79±5.52(5) 77.62±3.82(4) 78.35±4.22(3) 78.91±5.93(2) 79.90±4.13(1)
Haberman 62.65±6.25(4) 61.0±8.63(5) 65.11±13.65(2) 64.81±5.2(3) 65.94±9.49(1)
ORL 83.93±1.92(3) 82.56±2.29(5) 83.51±1.6(4) 87.84±1.86(2) 93.16±1.43(1)
Yeast 87.17±2.51(3) 87.73±2.51(1) 87.06±1.93(4) 86.88±1.48(5) 87.51±2.15(2)
Wilcoxon + + + + N/A
Ave.ACC 75.17 75.25 76.14 76.97 80.61
Ave.STD 3.23 3.30 4.17 3.12 3.36
4.2 Experimental Setup
In the experiments, five existing self-training
algorithms were selected for comparison in order to
verify the performance of the FSTDC algorithm. For
STDP and STDPNF, the parameter
∂ was set to 2.
The threshold parameter
θ was set to 0.1 for the
SETRED algorithm, while the STDEMB algorithm
was set to
k =7 and ∂ =0.5. These parameters
followed the settings in the original literature for each
algorithm. The significance of the experimental
results was verified by Wilcoxon test at 90%
A Parameter-Free Self-Training Algorithm for Dual Choice Strategy
105

confidence level. In the experimental results, the
symbol ‘+’ indicates that our algorithm performs
significantly better than the comparison algorithms;
‘-’ indicates that the performance is significantly
worse and ‘~’ indicates that there is no significant
difference in performance.
4.3 Analysis of Results
The table records the average accuracy of each
algorithm on different datasets, and our algorithm is
5.44%, 5.36%, 4.47%, and 3.64% higher than that of
the comparison algorithms, respectively, which
proves the effectiveness of our algorithm.
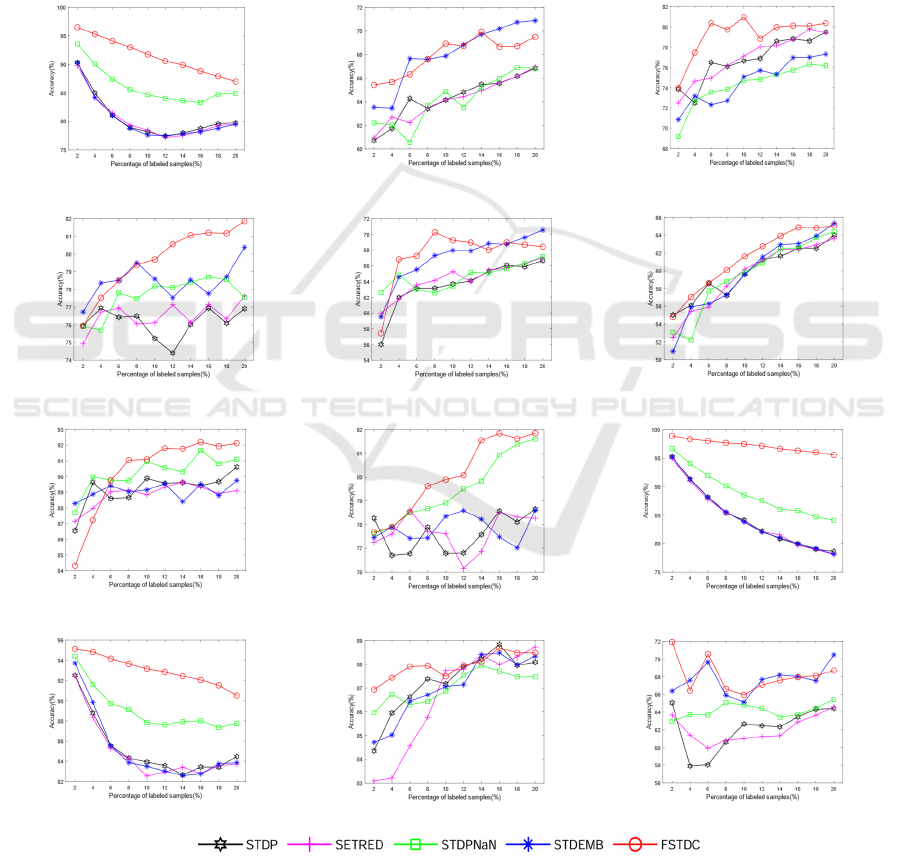
Meanwhile, we also did experiments on the effect
of the proportion of labeled samples on the
classification performance, and the experimental
results are shown in the figure below. From the figure,
it can be seen that with the increase of the proportion
of labeled samples, there is an upward trend in most
of the datasets.
AR Australian Balance
Cleve crx_uni BUPA
Ecoli Glass FERET32x32
ORL Yeast Haberman
Figure 1: Classification accuracies of six algorithms with different proportions of labeled samples.
DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems
106

5 SUMMARY
To address the problem of selecting high-confidence
samples for self-training algorithms in semi-
supervised learning, we propose a parameter-free
self-training algorithm for dual choice strategy
(FSTDC). FSTDC considers the local information of
the samples through the introduction of natural
neighbors and defines natural stable labels, which
take into account the information of the labeled
samples. In addition, high-confidence samples are
further selected by considering global information
through a dual strategy. Extensive experiments were
conducted and the experimental results proved the
effectiveness of our proposed algorithm.
REFERENCES
Van Engelen, J E., Hoos, H H., 2020. A survey on semi-
supervised learning. Machine learning, 109(2): 373-
440.
Li, M., Zhou, Z-H., SETRED: Self-training with
editing//Pacific-Asia Conference on Knowledge
Discovery and Data Mining, Springer: 611-621.
Wu, D., Shang, M., Luo, X., et al., 2018. Self-training semi-
supervised classification based on density peaks of data.
Neurocomputing, 275: 180-191.
Rodriguez. A., Laio. A., 2014. Clustering by fast search and
find of density peaks. science, 344(6191): 1492-1496.
Zhao, S., Li, J., 2021. A semi-supervised self-training
method based on density peaks and natural neighbors.
Journal of Ambient Intelligence and Humanized
Computing, 12(2): 2939-2953.
Li, J., Zhu, Q., Wu, Q., 2019. A self-training method based
on density peaks and an extended parameter-free local
noise filter for k nearest neighbor. Knowledge-Based
Systems, 184: 104895.
Wang, J., Wu, Y., Li, S., et al., 2023. A self-training
algorithm based on the two-stage data editing method
with mass-based dissimilarity. Neural Networks, 168:
431-449.
A Parameter-Free Self-Training Algorithm for Dual Choice Strategy
107