Research on Maneuver Decision of Unmanned Combat Aerial

Vehicles Based on Segmented Reward Function and

Improved Deep Q-Network

Juntao Ruan

1,2

, Yi Qin

, Fei Wang

, Jianjun Huang

, Fujie Wang

, Fang Guo

and Yaohua Hu

College of Electronics and Information Engineering, Shenzhen University, Shenzhen, China

School of Electrical Engineering and Intelligentization, Dongguan University of Technology, Dongguan, China

Harbin Institute of Technology, Shenzhen, China

Keywords: UCAV, Segmented Reward Function, EKF, DQN, Maneuvering Decision-Making.

Abstract: Intelligent air combat is the main trend in the future, and the maneuvering decision-making ability of

Unmanned combat aerial vehicles (UCAVs) affects the win-lose ending of the air battlefield. In order to

study the problem of maneuver decision-making in UCAV 1V1 air combat, this paper proposes a maneuver

decision generation algorithm based on the fusion of segmented reward function and improved deep Q-

network. Firstly, this paper establishes a real mathematical model problem in the complex environment of

air combat, and provides an equation expression that describes the spatial coordinate information, attitude

information velocity information of the current state of UCAVs. This expression can provide basic

maneuvering action instructions after passing the overload coefficient. Then, a segmented reward function

was designed to guide unmanned aerial vehicles to develop towards their own advantages in the turn of

aerial combat. Aiming at the problem of parameter uncertainty of deep Q-network (DQN) in maneuver

decision-making process, an improved deep Q-network algorithm is proposed in the next. By introducing

the extended Kalman filter (EKF), the uncertain parameter values of the strategy network are used to

construct the system state equations, the parameters of the target network are used to construct the

observation equations of the system, and the optimal parameter estimates of the DQN are obtained through

the iterative updating solution of EKF. Simulation experiments show the effectiveness of the designed

segmented reward function and the improved deep Q-network algorithm in autonomous maneuvering

decision-making for UCAVs.

1 INTRODUCTION

With the development of artificial intelligence

technology, the traditional form of war is evolving in

the direction of intelligence. As a typical equipment

of intelligent weapons, unmanned combat aerial

vehicles (UCAV) are likely to gradually replace

manned combat aircraft in the future and step by

step become the protagonist of future intelligent air

warfare (Cao et al., 2019). The intelligence of

UCAVs is mainly reflected in their autonomous

maneuvering decision-making ability in air combat,

which has received widespread attention. In future

intelligent air combat, the maneuvering decision-

making ability of UCAVs determines the outcome of

aerial combat. The autonomous maneuvering

decision-making of UCAVs in air combat essentially

relies on algorithms to evaluate the current air

combat situation and judge the quality of the current

combat environment (Zhang, 2022). Then, based on

the combat objectives and their own mobility, they

make maneuvering actions to achieve tactical attacks

or evasion effects. The autonomous maneuvering

decision-making use of aircrafts can improve the

aircraft's penetration and survival capabilities,

flexibility in executing complex tasks, and enhance

its concealment and adaptability (Yang et al., 2019).

Deep reinforcement learning (DRL) is a type of

artificial intelligence algorithm that is closer to

human thinking patterns. It can leverage the

advantages of deep learning in perceptual ability and

reinforcement learning in decision-making

problems. The combination of deep reinforcement

learning and UCAVs is an important trend in the

development of future air combat, which has a

Ruan, J., Qin, Y., Wang, F., Huang, J., Wang, F., Guo, F. and Hu, Y.

Research on Maneuver Decision of Unmanned Combat Aerial Vehicles Based on Segmented Reward Function and Improved Deep Q-Network.

DOI: 10.5220/0012911900004536

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Mining, E-Learning, and Information Systems (DMEIS 2024), pages 94-101

ISBN: 978-989-758-715-3

profound impact on enhancing military capabilities

and tactical innovation (Meng et al., 2022).

Recently, deep reinforcement learning technology

has made many improvements in algorithm theory,

forming a logically rigorous theoretical

foundation(Mnih et al., 2013). Scholars at home and

abroad have also made attempts to address the issue

of maneuver decision-making for UCAV, and have

achieved many results. The traditional methods for

generating maneuver decisions focus on expert

systems and matrix game algorithms. In addition,

artificial intelligence algorithms such as genetic

algorithms and particle swarm optimization

algorithms have also been applied in the field of

UCAV maneuver decision generation (Ernest et al.,

2016). However, the state of the air combat

environment has the characteristics of large space

and continuity, and the process of maneuver

decision-making still has research value (Sun et al.,

2009).

In this paper, based on the deep reinforcement

learning model elements to complete the abstract

modeling of intelligences, environments and actions,

the segmented reward function is redesigned to help

guide the unmanned fighter jet to select the correct

action. The accuracy of the output action value

function is ensured by introducing the extended

Kalman filter (EKF) to filter the parameters of the

deep Q network (DQN). On the basis of the DQN,

the system state equation is constructed using the

uncertain parameter values of the policy network,

the observation equation of the system is constructed

using the parameters of the target network, and the

optimal parameter estimation value of the DQN is

obtained by iteratively updating the EKF. Simulation

experiment show that the designed segmented

reward function and the DQN algorithm fused with

EKF are effective and reliable in autonomous

maneuver decision-making methods.

2 AIR COMBAT ENVIRONMENT

MODELING

2.1 Maneuvering Equations of UCAV

The maneuvering trajectory of UCAVs during air

combat can be seen as the result of each aircraft's

maneuvering command execution. The intuitive

manifestation of the maneuvering process of

UCAVs is the change in the trajectory of the

aircraft's maneuvering actions and the change in its

own attitude (Kung, 2018)

. UCAVs are objects that

are moving in the air and cannot be simply treated as

a particle. During the entire process of flying in the

air, for the position or azimuth relationship of the

movement, the aircraft can be treated as a particle

for speed or azimuth discrimination. The Euler angle

defines the attitude of an aircraft in three-

dimensional space, and the motion parameters of an

UCAV should also include the position information

of the aircraft in three-dimensional space, as well as

the velocity parameters of the aircraft. The

establishment of motion parameters helps to

describe the motion state of the aircraft, laying the

foundation for the subsequent control and maneuver

decision trajectory generation of UCAVs.

Figure 1: Ground coordinate system.

The kinematic equation of the aircraft's center of

mass can represent the relationship between the

aircraft's spatial position and time, meaning that the

aircraft's center of mass changes over time. The

equation set expression is defined as (1). In general,

this system of equations is established in a ground

coordinate system, as shown in Fig. 1.

cos cos

cos sin

sin



=⋅ ⋅



=− ⋅ ⋅





=⋅





(1)

where

, and

respectively represent spatial

coordinate values.

and

represent the pitch angle

and yaw angle of the UCAV, respectively.

Figure 2: Force analysis of UCAV.

For the convenience of research, it is assumed that

the thrust of the unmanned fighter jet engine always

Research on Maneuver Decision of Unmanned Combat Aerial Vehicles Based on Segmented Reward Function and Improved Deep

Q-Network

follows the direction of velocity, and the unmanned

fighter jet will not experience sideslip motion during

flight, without considering the impact of the angle of

attack on it (Kong et al., 2020). In addition, the land

in the flying airspace is a spatial plane. The force

analysis diagram of the UCAV in the air is shown in

Fig. 2. P represents the thrust of the aircraft engine,

D represents the resistance experienced by the

aircraft, and L represents the lift of the aircraft.

Given the above assumptions, a simplified system of

aircraft motion dynamics equations can be derived.

The expression of the aircraft motion dynamics

equation is shown in (2). Although it has been

simplified, it still helps to study the maneuvering

and flight trajectory problems of UVAVs.

sin

cos cos

cos sin

mPDmg

mV L mg

mV L

θγ



=−−



=⋅ − ⋅





−⋅ =⋅





(2)

Where,

is the roll angle of UCAV. The first

equation in the system represents the change in

aircraft speed. The second and third equations

represent the changes in pitch angle

and yaw

angle

of UCAV in the vertical plane, respectively.

When flying in the air, the aircraft is subjected to

external forces such as engine thrust, air lift, and its

own gravity. The overload coefficient can express

the ratio of the combined external force of an UCAV,

excluding gravity, to the gravity acting on the

aircraft. The expression formula is shown in (3).

cos

sin



−



⋅





⋅





(3)

where

is the tangential overload of the aircraft,

along the direction of velocity.

n and

are

perpendicular to the direction of velocity. The

combination of

n and

defines the normal

overload

n , as shown in (4).

fyz

nnn

=+=

(4)

Substituting tangential overload and normal

overload into the motion dynamics equation of the

UCAV can be obtained in (5).

(sin)

(cos cos)

sin

cos

dt v

dt V



=−



=−





=− ⋅



⋅



(5)

where, the first equation in (5) describes the

relationship between the change in aircraft speed and

the tangential overload of the aircraft when the pitch

angle is determined; The second and third equations

of the system explain the influence of normal

overload and roll angle on the pitch and yaw angle

changes of the aircraft, respectively.

If the tangential overload, normal overload, and

roll angle are set properly, the basic flight actions of

the UCAV can be obtained based on the numerical

values of these variables. Therefore, based on the

size of the variable values, 11 basic aircraft

maneuvers can be selected, among which maneuvers

involving overload are all carried out at maximum

overload.

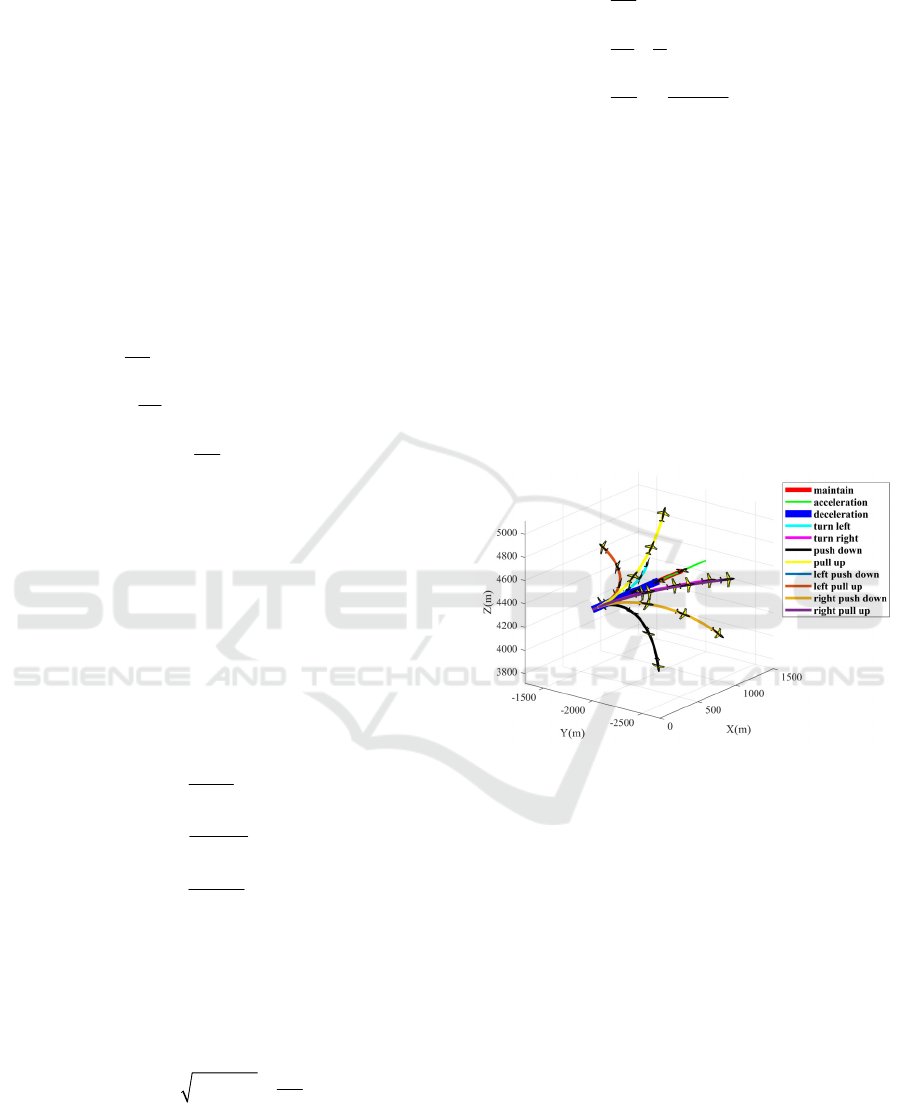
Figure 3: Basic maneuvers of UCAV.

The flight maneuver trajectories in Fig. 3

represent respectively the UCAV maintaining a

constant speed forward flight, accelerating forward

flight, decelerating forward flight, turning left

horizontally, turning right horizontally, push down

on a vertical plane, pull up on a vertical plane, push

down in the downward left direction, pull up in the

upward left direction, push down in the downward

right direction, and pull up in the upward left

direction.

2.2 Air Situation Assessment

The UCAV fighting process in air combat is variable

and complex. In the one-on-one fighting between the

red and blue sides, the respective UCAVs need to

assess the current combat environment in order to

make reasonable and effective maneuvers to put

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

themselves in the advantageous side of the battle and

avoid being attacked by the local area. In addition,

the air combat situation assessment is a dynamic

process, the current situation value will be changed

with the UCAV maneuvers, which requires the

situation evaluator to conduct real-time correct

assessment of the current air.

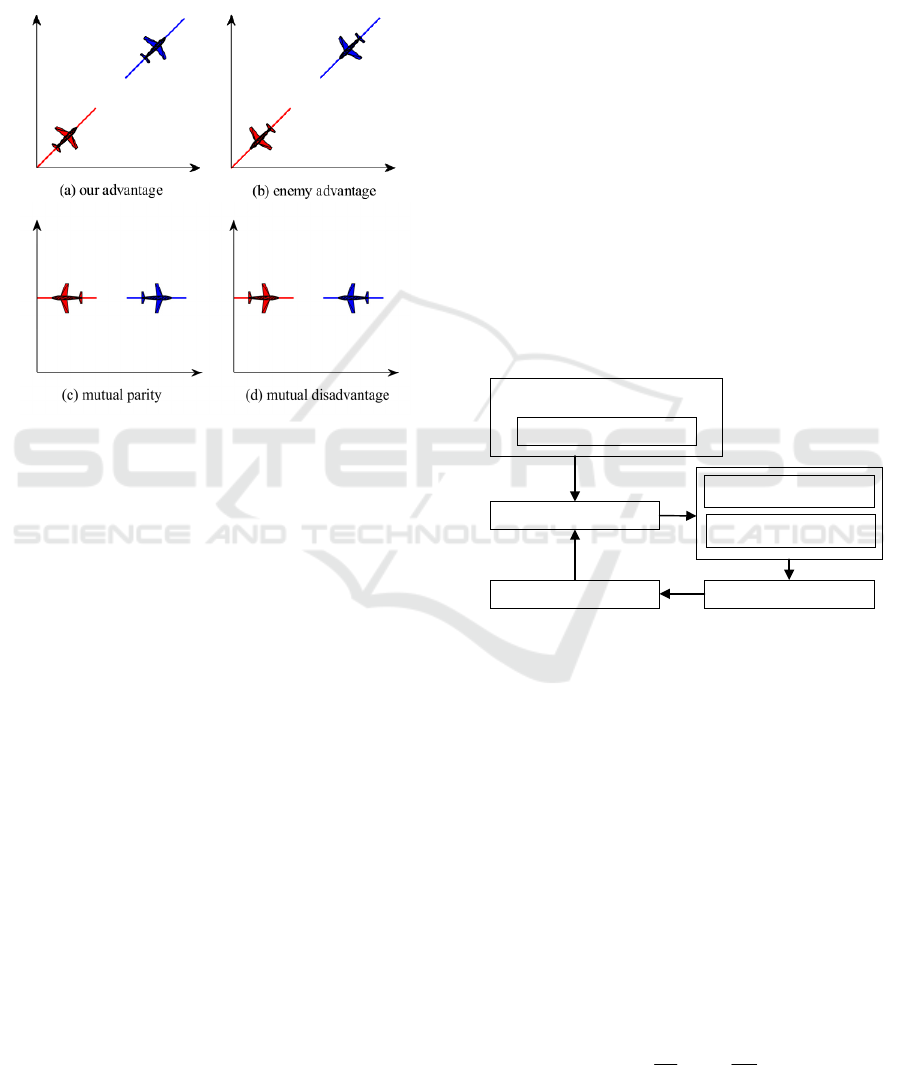
Figure 4: Situation types of air combat.

The geometric orientation relationship between

the two UCAVs describes the current type of

situation in the air, where two are closely related.

Based on this two-angle relationship the situational

types of air combat are categorized into four types,

as shown in Fig. 4: our advantage, enemy advantage,

mutual parity, and mutual disadvantage. The

selection of the situational type is helpful for

subsequent reward evaluation, rapid adjustment of

maneuver strategies, and improvement of efficiency.

3 MANEUVERING

DECISION-MAKING

ALGORITHM

3.1 Maneuvering Decision-Making

Process

The OODA loop is named after the combination of

the first letters of four words: observation,

orientation, decision and action. In the research of

UCAV maneuvering decision-making, the OODA

loop provides a strong and powerful framework to

help understand and guide the maneuver decision

process. During the observation phase, UCAVs need

to collect real-time information from the air combat

environment, including location information of

enemy or friendly states and spatial environment

information. In the judgment stage, UCAVs need to

combine some past experiences, lessons learned or

theoretical knowledge, learn to analyze the

information obtained during the observation stage,

understand their own environment, and predict

future development trends, providing a basis for the

next decision-making process. In the decision-

making stage, the UCAV makes the best maneuver

decision based on the judgment from the previous

step. This decision should either achieve the

established goals and tasks or eliminate temporary

dangerous situations. In the action phase, UCAVs

perform selected maneuver actions on the decision-

making phase to make changes to their current state.

Subsequently, the unmanned aerial vehicle once

again entered the observation phase to verify the

effectiveness of maneuver decisions and make

timely adjustments according to requirements. So,

the UCAV maneuvering decision-making process is

shown in Fig. 5 below.

Air combat environment initialization

Air situat ion assess ment

UCAV model initialization

Maneuver action execution

Status environment update

Maneuver action selection

Reward information update

Figure 5: Maneuvering decision-making process.

3.2 Segment Reward Function Design

The design of reward function is the core of the

entire intelligent agent learning process. The reward

function defines the target for each maneuver of an

UCAV in intelligent air combat. A reasonable

reward function can guide our aircraft's maneuvers

towards a greater advantage until we successfully

shoot down the enemy. The energy concentration of

aircraft in air combat is reflected in gravitational

potential energy and kinetic energy. Based on the

positional relationship between two aircraft in air

combat situation assessment, the reward function

design is divided into four parts: angle reward

function, velocity reward function, altitude reward

function, and distance reward function.

cos( ) cos( ) 1

att esc

r =+ −

(6)

Research on Maneuver Decision of Unmanned Combat Aerial Vehicles Based on Segmented Reward Function and Improved Deep

Q-Network

where,

is angle reward value.

att

is the angle

between the connection between the red-blue aircraft

and our flight speed.

esc

is the angle between the

connection between the blue-red aircraft and the

enemy's flight speed.

tan ,

2tan ,

others

hhorhh







Δ−



−Δ>Δ<





(7)

where,

is altitude reward value. hΔ is the

height difference between two aircraft, and

represents the upper and lower limits of the height

difference. Once this limit is exceeded, a certain

punishment reward will be given. In addition,

k in

(7) represents an adjustment parameter that can assist

in correcting the shape of the reward function curve.

The velocity reward function and altitude reward

function of an UCAV can be calculated using the

same method, as they both represent different forms

of aircraft energy. Velocity reflects kinetic energy,

while altitude reflects gravitational potential energy.

Therefore, the velocity reward function is shown in

(8).

tan ,

2tan ,

others

vvorvv







Δ−



−Δ>Δ<





(8)

The distance reward function is used to guide

enemy UCAV to fall into the attack direction of our

side. Once the distance between two UCAVs is too

large, the aircraft's maneuvering decision-making

actions will become meaningless.

()

eddordd

others

−





−Δ> Δ<







(9)

where,

represents the boundary value of the

optimal attack interval.

is one of the parameters of

an exponential function, which can achieve scaling

transformation of distance rewards, but the trend of

curve change remains unchanged.

Based on the four segmented sub reward

functions mentioned above, the average sum can be

used to obtain a single step comprehensive reward

for the maneuvering action of an UCAV.

3.3 Improved Deep Q-Network

Deep Q-network (DQN) is an algorithm that

combines deep learning and reinforcement learning.

It was proposed by DeepMind's research team in

2015 to solve decision problems with high-

dimensional observation spaces (Kumar et al., 2021).

The core idea of DQN is to use deep neural

networks to approximate the Q function, which is

the value function and predicts the expected return

that can be obtained by taking specific actions under

a given state. By leveraging the excellent ability of

DQN in dealing with high-dimensional spatial

problems, we use DQN to characterize the one-on-

one combat environment between red and blue sides.

The state space s is composed of parameters such as

the flight speed, three-dimensional coordinate

information, and attitude related Euler angles of

UCAV. Action a is the action that an UCAV needs

to take after sensing a change in the air combat

situation, and can be selected from the basic set of

UCAV maneuver instructions.

So, using the standard DQN algorithm for UCAV

maneuvering decision-making will follow the

following three steps, as follows.

Step 1: Initialize. Set the motion parameters of the

red and blue aircrafts. Initialize an experience pool

to store combat trajectory information for each

episode. Initialize the Q-network (main network)

and the target Q-network (target network), both of

which have the same architecture but different

parameters.

Step 2: Maneuver action. Based on the current

status, use ε-greedy strategy selects a maneuver.

Then, we observe the single step reward and new

state. Store the experience set (state, action, reward,

new state) in the experience pool.

Step 3: Learn and train. Randomly sample a small

batch of experiences from experience pool. For each

experience sample, calculate the target Q value.

Calculate the loss function using these target Q

values and the current predicted Q values of the

main network. By using gradient descent to update

the weights of the main network, the goal is to

minimize the difference between the predicted Q

value and the target Q value, in order to minimize

the loss function.

Although DQN introduces the target network to

provide a relatively stable learning objective, the

target Q value changes with the update of online

network parameters, which may lead to unstable

learning processes. Therefore, we introduce

extended Kalman filtering (EKF) into the model of

deep Q-networks to solve the problem of parameter

uncertainty. EKF is an algorithm used for state

estimation of nonlinear system (Zhou et al., 2020). It

is a nonlinear version of the Kalman filter, which

approximates the state transition and observation

model of a nonlinear system by using Taylor series

expansion. The goal of reinforcement learning is to

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

learn a Q function, denoted

(, ; )Qsa

. We can

consider the network parameters as the system states

and the Q values as observations, and thus use the

EKF to infer and update the network parameters.

The state and observation equations are shown in

(10) below.

(, )

(,) (,;)

ttttt

ttt tttt

zh v Qsa v

θθωθω

θθ

==+





== +



(10)

where,

represents the time step.

is process

noise in the state equation

, following a normal

distribution

(0, )

;

is the measurement noise in

observation equation

, following a normal

distribution

(0, )



∂

(11)



∂

(12)

For the observation model, the Jacobian matrix

is shown in (13).



∂

(13)

Use the linearized state transition model to

predict the state of the next time step, as shown in

(14).



|1tt t

ttt

θθω

−

(14)

The covariance of the predicted state estimation

is shown in (15).

tt t t t t

PFPFQ

−

(15)

where,

is the covariance matrix of the previous

time step, and

is the covariance matrix of the

process noise.

In the observation update step, it is necessary to

calculate the observation residual using the (16).

Calculate the Kalman gain K as shown in (17).



(,)

tt t

yzh v

−

=−

(16)

|1 |1

()

t ttt tttt t

KPHHPH R

−

−−

(17)

where,

is the covariance matrix of the

observation noise. Using Kalman gain, the EKF

updates the state estimates, making the estimates

closer to the actual observations. Update formula

such as (18).



|1ttt

θθ

−

(18)

Finally, update the covariance matrix of the state

estimation, which takes into account the impact of

observation updates on uncertainty, as shown in (19)

()

ttttt

PIKHP

−

=− (19)

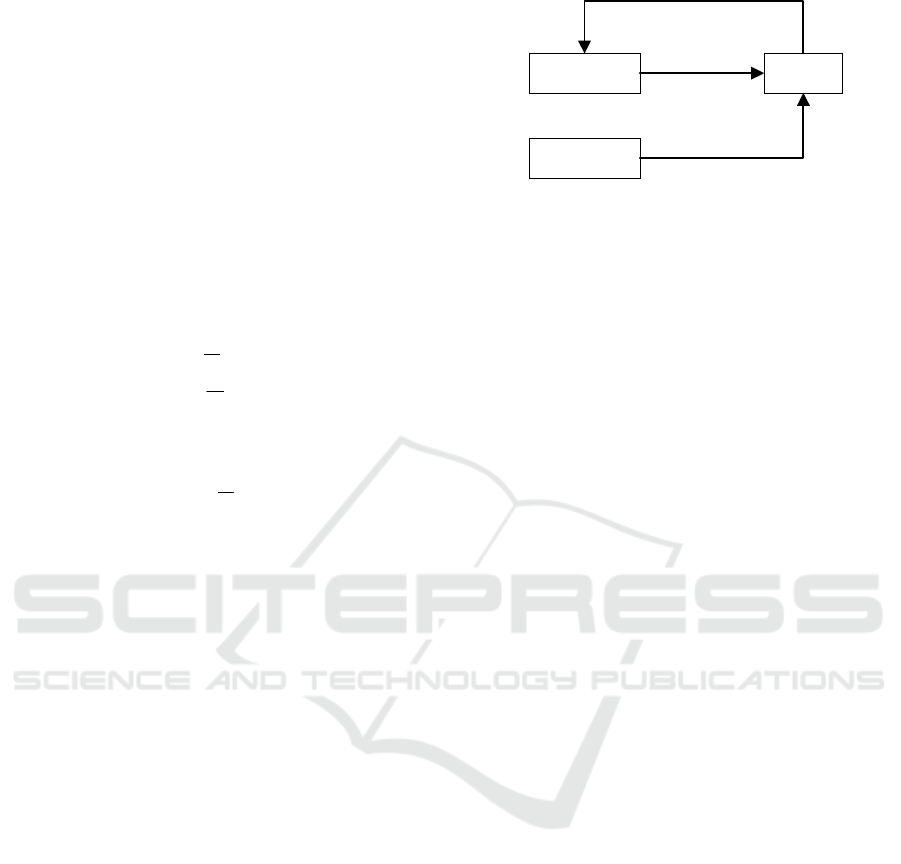
Current

Q-network

Target

Q-network

EKF

(, ; )

ttt

Qs a

Figure 6: Structural diagram of the combination of DQN

and EKF.

Overall, the implementation method for

improving deep Q-network is to combine the direct

copying process of DQN parameters with an EKF.

At the beginning of the network training, the state

and observation equations of the EKF are

constructed using the parameters

and

(, ; )

ttt

Qs a

of the Q-network at the moment t. The Kalman gain

of the extended Kalman filter is used to estimate the

true parameters of the Q network. By continuously

iterating and updating the Kalman gain, the error in

obtaining true parameter estimates is minimized.

Finally, the filtered Q-network parameters are

transmitted to the target network to improve the

effectiveness of UCAV maneuver decision-making.

The algorithm flowchart combining DQN and EKF

is shown in Fig. 6.

4 SIMULATION EXPERIMENTS

4.1 Simulation Environment Setting

In the simulation combat phase, our UCAV is

represented in red, while the enemy is represented in

blue. The combat flight trajectory of two aircrafts is

a continuous process, but it requires setting

termination conditions for each combat turn. In the

simulation process, the maneuver decision cycle of

the UCAV is 0.25 second, which means there are

four opportunities to change the maneuver action

every minute. Each air combat episode needs to have

a termination condition, otherwise the training of the

Q-network cannot proceed. The maximum number

of maneuvering steps for an air combat episode is

250. When reaching 250 steps, forcibly withdraw

from the current episode of combat, hoping that the

final trained network can quickly determine the

winner in air combat. So, the rules for determining

the winner are as follows. If the attack angle of our

UCAV is less than 60 ° and the escape angle is less

than 30 ° within the limited number of maneuver

Research on Maneuver Decision of Unmanned Combat Aerial Vehicles Based on Segmented Reward Function and Improved Deep

Q-Network

decision steps, and our side meets the appeal

conditions for more than 9 maneuver steps within

this attack range, it will be judged as our victory and

the current combat round will end. This situation is

similar to the radar of airborne weapons firmly

locking enemy aircraft.

Additionally, in one-on-one air combat, it is

assumed that the maneuver ability of two aircraft is

consistent. The DQN adopts the ε-greedy strategy

for early exploration, and begins to reduce the

degree of exploration after the experience pool is

full. The DQN discount return is 0.9, the learning

rate is 0.008, and the experience pool capacity is

20000. After storing 1000 samples, start training the

Q-network, with a sample size of 64 extracted each

time. The target network is updated every 4 air

combat episodes.

In order to ensure that UCAVs can learn

excellent maneuver decision-making experience in

the network, red and blue aircrafts were designed to

be in a mutually parity situation. In the initial stage,

both the red and blue sides have the same flight

speed and altitude. But their initial flight direction is

in the same straight line and opposite. The starting

parameters of the UCAVs are shown below.

Table 1: UCAV initial value setting in heading dilemma.

Initial

Va lu e



-1

(, ,)

/ m

(, ,)

ψγ

rad

Red

250 (0,0,6000)

(0,

−

,0)

Blue

250 (2000,2000,6000)

(0,

−

,0)

4.2 Simulation Experiment Analysis

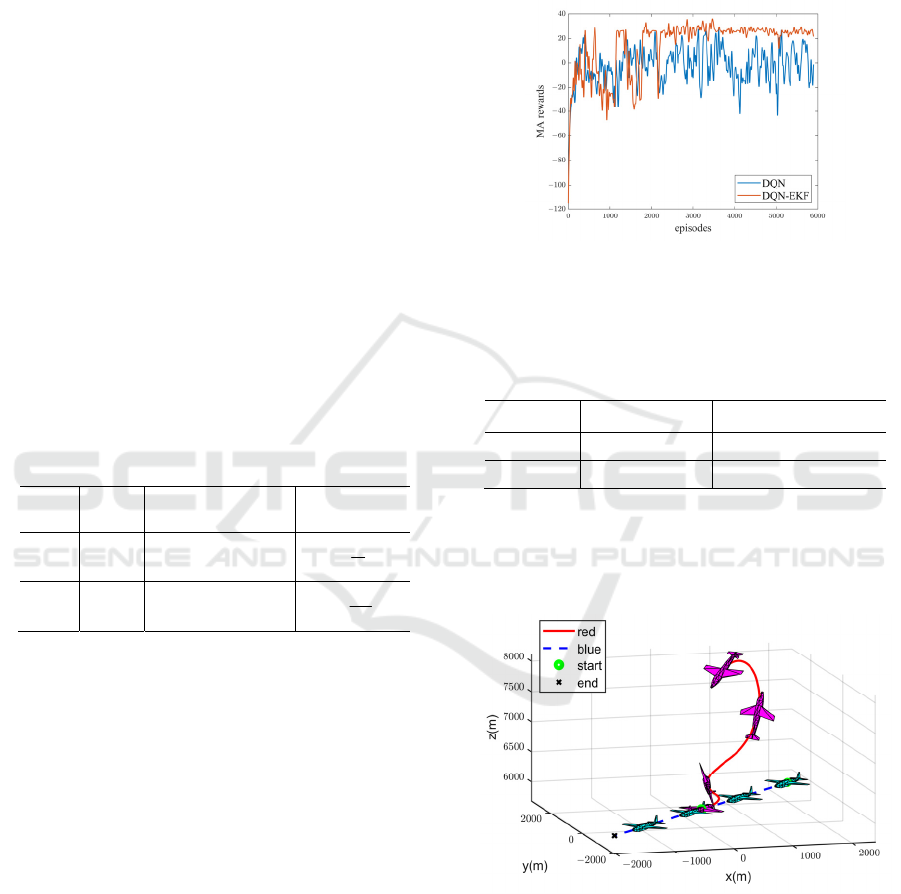
Train the UCAV maneuver decision generation

algorithm according to the designed motion

parameters and the preset parameters of the Q-

network. After 6000 rounds of training, the average

episode reward value during the training process was

obtained. The comprehensive reward curve for our

UCAV's turn is shown in Fig. 7. The blue curve in

figure represents the unmodified DQN training

result curve, while the red curve represents the

improved DQN algorithm training result fused with

EKF.

It can be clearly seen from the Fig. 7 that as the

training iterations progress, the average episode

reward value has rapidly improved compared to the

beginning of the training. Because in the initial stage

of training, UCAVs are still in the stage of exploring

the environment. Compared to traditional DQN, the

rewards trained by DQN-EKF method achieve high

returns in the later stages and are also more stable.

The training results demonstrate the feasibility of

DQN-EKF in solving the autonomous maneuver

decision generation problem of unmanned aerial

vehicles.

Figure 7: Reward curve for each episode.

The difference in average episode reward data for

training iterations is shown in Table 2.

Table 2: Algorithm differences data.

algorithm Average reward Standard deviation

DQN

-2.3079 13.9051

DQN-EKF

15.2013 3.7112

In calculating the standard deviation, the average

reward of the second half of the turn was selected.

Because the reward value at the beginning of the

training is rapidly increasing.

Figure 8: Maneuver strategy generated by DQN-EKF.

Save the training model of the network, and for

the red and blue sides in an opposing flight state, the

maneuver trajectory generated by DQN-EKF is

shown in Fig. 8. At the beginning of this round of

battle, the red side first made a left turn maneuver to

get rid of the enemy's attack. Then, the red side

continues to pull up, which can be seen as a typical

DMEIS 2024 - The International Conference on Data Mining, E-Learning, and Information Systems

100

tactical maneuver of completing a somersault. Next,

complete the attack on the enemy during the dive to

level flight phase. The maneuver actions in this battle

round are sufficient to demonstrate the effectiveness

of the maneuver strategy generated by the DQN-EKF

fusion algorithm.

5 CONCLUSIONS

As air combat moves towards intelligence, this paper

conducts research on maneuver decision-making for

UCAVs in close range scenarios, and proposes an

UCAV maneuver decision-making algorithm based

on the fusion of segmented reward functions and

improved deep Q-networks. Specifically, we

conduct mathematical modeling on UCAVs as

intelligent agents for deep reinforcement learning,

and derive the process of aircrafts maneuvering in

the air. A segmented reward function was designed

to guide UCAVs to perform the most advantageous

maneuvers during the turn of aerial combat.

Introducing extended Kalman filtering to solve the

problem of parameter uncertainty in Q-network

maneuver decision-making process, and utilizing

improved deep Q-network to generate maneuver

decisions. Simulation comparative experiments

show that the DQN-EKF algorithm can increase and

stabilize the average turn reward of aerial combat,

providing new ideas for maneuver decision-making

problems. In the future, we can conduct multi

aircraft collaborative research around the attack

missions of unmanned combat aerial vehicle

formations.

ACKNOWLEDGEMENTS

This research is supported by the Guangdong

Provincial Department of Education Innovation

Strong School Program under Grant

2022ZDZX1031 and 2022KTSCX138, by R&D

projects in key areas of Guangdong Province,

2022B0303010001, by National Natural Science

Foundation of China under Grant 62203116 and

62103106.

REFERENCES

Cao, Y., Wei, W., Bai, Y., Qiao, H., 2019. Multi-base

multi-UAV cooperative reconnaissance path planning

with genetic algorithm. Cluster Comput, vol. 22, no.

s3, pp. 5175-5184.

Zhang, Y., 2022. Accuracy assessment of a UAV direct

georeferencing method and impact of the

configuration of ground control points. Drones, vol. 6,

no.2, pp.30.

Yang, Q. , Zhang, J. , Shi, G., Hu, J., Wu, Y., 2019.

Maneuver decision of UAV in short-range air combat

based on deep reinforcement learning. IEEE Access,

vol. 8, pp. 363-378.

Meng, H., Sun, C., Feng, Y., Fang, Q., 2022. One-to-one

close air combat maneuver decision method based on

target maneuver intention prediction. In 2022 IEEE

International Conference on Unmanned Systems

(ICUS), Guangzhou, China: IEEE, pp. 1454-1465.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., Riedmiller, M., 2013.

Playing atari with deep reinforcement learning. arxiv

preprint arxiv:1312.5602.

Ernest, N., Carroll, D., Schumacher, C., Clark, M., Cohen,

K., Lee, G., 2016. Genetic fuzzy based artificial

intelligence for unmanned combat aerial vehicle

control in simulated air combat missions. Journal of

Defense Management, vol. 6, no. 1, pp. 2167-0374.

Sun, Y., Zhou, X., Meng, S., 2009. Research on

maneuvering decision for multi-fighter cooperative air

combat. In 2009 International Conference on

Intelligent Human-Machine Systems and Cybernetics,

Hangzhou, China: IEEE, 2009, pp. 197-200.

Kung, C., 2018. Study on consulting air combat simulation

of cluster UAV based on mixed parallel computing

framework of graphics processing unit. Electronics,

vol. 7, no. 9, pp. 160-184.

Kong, W., Zhou, D., Yang, Z., Zhang, K., Zeng, L., 2020.

Maneuver strategy generation of ucav for within visual

range air combat based on multi-agent reinforcement

learning and target position prediction. Applied

Sciences, vol. 10, no. 15, pp. 5198.

Kumar, S., Punitha, S., Perakam, G., Palukuru, V. P.,

Raghavaraju, J., Praveena, R., 2021. Artificial

intelligence (AI) prediction of atari game strategy by

using reinforcement learning algorithms. In 2021

International Conference on Computational

Performance Evaluation (ComPE), Shillong, India:

IEEE, 2021, pp. 536-539.

Zhou, Y., Ozbay, K., Cholette, M., Kachroo, P., 2020. A

mode switching extended kalman filter for real-time

traffic state and parameter estimation. In 2020 23rd

IEEE International Conference on Intelligent

Transportation Systems(ITSC), Rhodes, Greece: IEEE,

2020, pp. 1-8.

Research on Maneuver Decision of Unmanned Combat Aerial Vehicles Based on Segmented Reward Function and Improved Deep

Q-Network

101