Evaluating the Relative Importance of Product Line Features

Using Centrality Metrics

Fathiya Mohammed

, Mike Mannion

, Hermann Kaindl

and James Paterson

School of Computing, Engineering & Physical Sciences, University of West of Scotland, Paisley, U.K.

Department of Computing, Glasgow Caledonian University, 70 Cowcaddens Road, Glasgow, G4 0BA, U.K.

Institute of Computer Technology, TU Wien, Austria

Keywords: Feature Model, Centrality Metrics, Product Line.

Abstract: A software product line is a set of products that share a set of software features and assets, which satisfy the

specific needs of one or more target markets. One common artefact of software product line engineering is a

feature model, usually represented as a directed acyclic graph, which shows the product line as a set of

structural feature relationships. We argue that there are benefits to considering a feature model as a directed

graph and an undirected graph, respectively. One element of managing the impact of a change to these models,

as they increase in complexity, is to evaluate the relative importance of the features. This paper explores the

application of centrality metrics from social network analysis for the identification of the relative importance

of features in feature models. The metrics considered are degree centrality, closeness centrality, eccentricity

centrality, eigenvector centrality and between-ness centrality. To illustrate, a product feature model is

constructed from a real-world GSMA AI-mobile phone product line requirements specification.

1 INTRODUCTION

A software product line is a common platform to

develop a family of products at lower cost, reduced

time to market and with better quality (BS ISO 2017).

The discipline of systematically planning,

constructing, evolving and managing that set of

products is known as Software Product Line

Engineering (SPLE). In SPLE, a product line feature

model consists of a hierarchy of features with some

additional cross-cutting relationships.

Over time, within a product line organisation, as

the volume and variety of products increase in scope

and scale, and personnel come and go, the risk of the

organization not fully understanding the product line

increases. Feature model analysis methods and tools

can help mitigate that risk. Feature models are usually

represented as (directed acyclic) graphs. Graphs can

represent application problems in many fields e.g.

city networks, biological networks, social media.

Feature model analysis can benefit from graph

https://orcid.org/0009-0004-7563-5614

https://orcid.org/0000-0003-2589-3901

https://orcid.org/0000-0002-1133-0529

https://orcid.org/0000-0002-6955-1009

analysis theory.

There can be different purposes for analyszing a

feature model. (Benavides, 2010) provides a review

of automated approaches to analysis for discovering

valid product configurations and managing them

effectively. Other purposes include conducting an

impact analysis of a change to the model, planning the

introduction of a new product, or making a

comparison of products configured from the model.

Within most product lines, some features are

often perceived by different stakeholders as having a

different level of importance than others. A high

relative importance might be attributed, for example,

to a feature being a key differentiator in its market

sector, of significant value to a key customer, a

significant conduit for communication between other

features, or as start of a set of features whose design

will be allocated to an external third party. Often,

during feature model analysis, the greater the relative

importance of a feature, the more attention it receives

and the more influence it has on the analysis outcome.

Mohammed, F., Mannion, M., Kaindl, H. and Paterson, J.

Evaluating the Relative Importance of Product Line Features Using Centrality Metrics.

DOI: 10.5220/0012853300003753

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Conference on Software Technologies (ICSOFT 2024), pages 469-476

ISBN: 978-989-758-706-1; ISSN: 2184-2833

469

Some characteristics that contribute to the

calculation of a feature’s relative importance can be

determined by its semantic properties e.g. its

significance to a key customer. Other characteristics

can be determined by its structural properties within

the model e.g. how many features depend on it. For a

product line that contains thousands of features the

calculation of relative importance values is only

practical when done automatically.

Different structural graph analysis metrics afford

an insight into the scope and scale of an application

problem. They are a useful aid when the scale and

scope of the graph make visual inspection unwieldy.

In social network analysis (Scott, 2017) centrality

metrics provide an assessment of each vertex’s

structural relative importance within a graph i.e. its

“centrality” to the graph.

This paper explores the application of several

centrality metrics to help identify the relative

importance of different features in a product line

feature model. The metrics considered are: degree

centrality, close centrality, eccentricity centrality,

eigenvector centrality and between-ness centrality.

Our research question is:

RQ1: What are the effects of different metrics for

calculating a feature’s relative importance

in a software product line?

We address this question by constructing a feature

model from a real-world product line requirements

specification and examining the value of the metrics.

Section 2 reviews the representation of a product

line feature model as a graph to make this paper self-

contained. Section 3 introduces a real-world product

line specification for next generation mobile phones.

Section 4 shows the calculations for centrality

metrics. Section 5 presents the application of the

metrics to the mobile phone specification. Section 6

discusses the the findings. Section 7 refers to related

work. Section 8 draws some conclusions.

2 SPL FEATURE MODELS

Feature models are often large and complex and many

factors affect their design e.g. graphical notation,

language rigour, tool support availability, ease of

comprehension, navigation difficulty, encoding

simplicity, analysis complexity, and product

configuration process. A feature model is often

constructed as a set of structural feature relationships

organized in a hierarchical graph with some abstract

features that aid modelling but are unimplemented.

The most popular graphical representation of a

feature model is a tree with additional crosscutting

relationships between nodes (Appendix 1), resulting

in an undirected acyclic graph.

Expressing crosscutting relationships between

features in different parts of the graph is hard and

often done separately in text. In (BS ISO, 2017) such

relationships are restricted to requires and excludes.

Sometimes, these relationships are so complex that

product-preserving transformation mechanisms are

needed to convert them into a feature modelling

language (Knuppel et al, 2017) to make processing

easier albeit longer

Product configuration is the task of selecting

features for a product from the feature model. During

selection, the feature model can be traversed using

different methods. Regardless, selection decisions are

largely governed by a feature’s variability type. This

property anticipates that not all features will appear in

every product. Domain engineers who construct and

maintain a feature model allocate values to feature

variability-type properties based on the existing

product portfolio and product roadmaps. Over the

lifecycle of a product line, for any individual feature,

the value of its variability-type property may also

change as features move in and out of popularity.

Table 1 shows four commonly used variability

types (BS ISO, 2017). When a feature is selected and

its variability type is Mandatory, it is automatically

selected. When a feature is selected and its variability

type is Exclusive-OR then only one of the set of

mutually exclusive features must be selected. When a

feature is selected and its variability type is Inclusive-

OR then one, some or all must be selected. When a

feature is selected and its variability type is Optional,

then it can be selected or not.

Table 1: Description of Variability Type.

Variability Type Description

Mandatory

A mandatory feature is automatically

selected.

Exclusive-OR

A set of choices which are mutually

exclusive and only one must be selecte

Inclusive-OR

A set of choices of which one, some or all

must be selected

Option

A single choice which may or may not be

selected

A feature model is sometimes implicitly

considered a directed graph because some features

are regarded as parents and some as children, In an

undirected graph, edges represent a two-way

connection between features. Deciding if a product

line feature model an undirected or a directed graph

can vary depending on the purposes of the modelling.

ICSOFT 2024 - 19th International Conference on Software Technologies

470

3 GSMA APPLICATION

The Global Systems for Mobile communications

Association (GSMA) is a worldwide industry trade

body to support and promote the interests of hundreds

of mobile operators. Its purposes include easing

cooperation between countries deploying GSM

technology, facilitating protocols and standards,

supporting interoperability, and encouraging

innovation across the mobile ecosystem.

In July 2023, to accelerate the deployment of AI

technology across the industry, GSMA published a

non-confidential Artificial Intelligence (AI) Mobile

Device Requirements Specification (GSMA, 2023).

In effect, it specifies a set of product line

requirements. Actual products derived from this

specification will have some but not all of the features

this specification points to. In the specification,

readers are directed to (Bradner, 1997) to understand

the interpretation of the keywords “MUST”, “MUST

NOT”, “REQUIRED”, “SHALL”, “SHALL NOT”,

“SHOULD”, “SHOULD NOT”,

“RECOMMENDED”, “MAY” and “OPTIONAL”.

We used this specification to construct a feature

model. We introduced some abstract features in the

model to aid modelling and understanding, but they

would not be implemented in any product. We gave

each requirement an identifier. A full list showing

how we labelled each requirement in the specification

and where we introduced some abstract requirements

is at https://figshare.com/s/1475000bed40c6f7bc56.

We did not have access to the authors of this

document so in structuring the feature model and

allocating a variability type for each feature (using

Table 1) we used our own interpretation and do not

claim it to be the best.

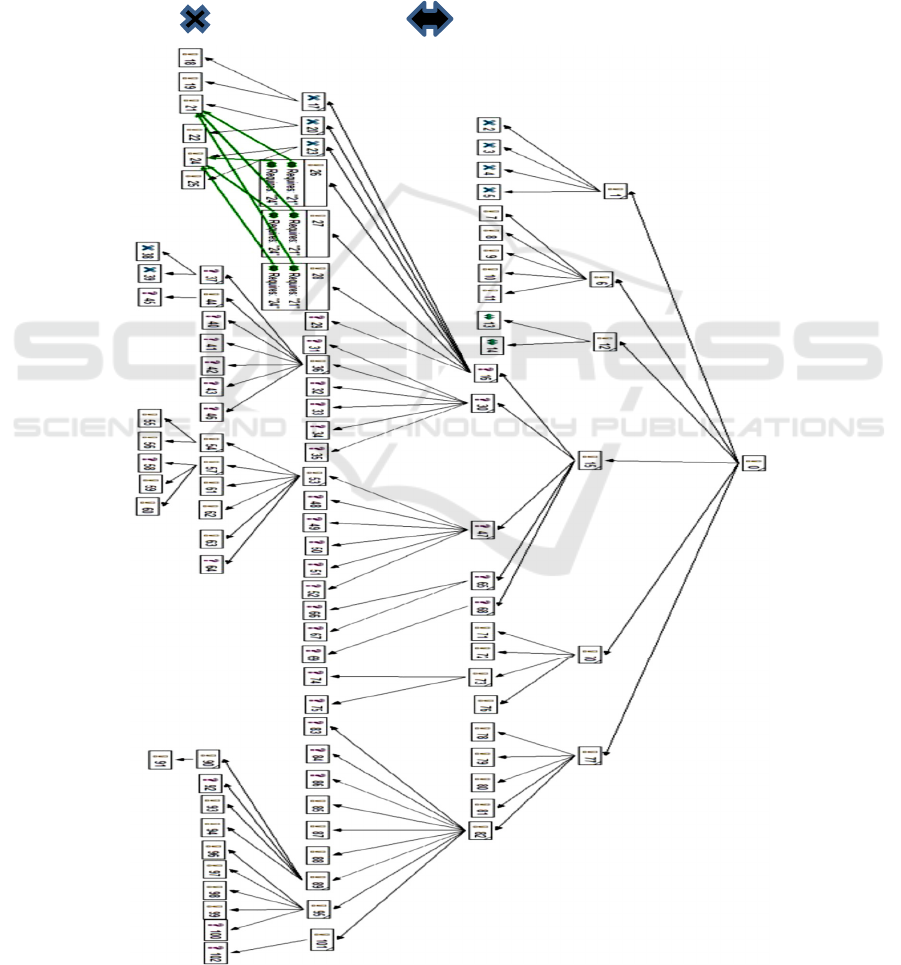
Appendix 1 shows a feature model. It uses the

notation of the tool it was constructed with,

pure::variants (Pure Systems, 2024). Many feature

models are implicitly assumed to be directed graphs

because they adopt the guidance in (Lee et al, 2002)

i.e. the model captures structural or conceptual

relationships among features e.g. a composed-of

relationship, a generalization-specialization

relationship, an implemented-by relationship which in

turn assumes information flow direction. In practice,

when analysing a feature model the comprehension

process is iterative and includes viewing the model as

a directed and an undirected graph.

To illustrate product configuration, let us assume

for simplicity that the GSMA feature model is

traversed depth-first starting at Feature 0. Feature 1 is

considered first and selected automatically because it

is Mandatory a. Next, one or more of Features 2, 3, 4,

5 are selected because their variability type is

Inclusive-OR. Feature 6 is selected automatically

because it is Mandatory. Then, one or more of

features 7, 8, 9, 10, 11 are selected because their

variability type is Inclusive-OR. Feature 12 is

selected automatically because it is mandatory. Then

either Feature 13 or Feature 14 is selected because

their variability-type is Exclusive-OR. The process

continues until all selections have been made.

4 DETERMINING A FEATURE’S

RELATIVE IMPORTANCE

The process of allocation of a relative importance

value to a feature is undertaken before feature

analysis takes place. Importance is normally

represented by attaching a weight to a feature and/or

to the edges connecting it. Maintaining agreement on

weights allocation is difficult for many reasons

including the different perspectives of organizational

stakeholders, changes to the model, having people

who work on the product line come and go over time.

Collectively, they motivate seeking an automatic

weight allocation method.

Social Network Analysis (Scott, 2017) is the

discipline of analyzing the relationships of interaction

among actors in a social network. A network is

arranged as a graph with vertices and edges

connecting the vertices. Important vertices are

typically those which maintain the graph’s

cohesiveness, or are significant information conduits

from lying on pathways through which other vertices

are reached. Normally, the higher the connectivity of

a feature the greater is its relative importance.

In a product line feature model, a vertex is a

feature. Centrality metrics can provide an assessment

of each feature’s relative importance within a feature

model. There are many centrality metrics, each one a

function of the number of connections a feature has

to other features and the strength of each connection.

Connectivity can be measured in different ways,

reflecting an understanding that a feature might be

strongly connected locally within the graph but

weakly connected globally, or vice-versa. Some

metrics also consider connectivity to highly important

features wherever they are in the graph. Such features

may exist a priori from the graph structure e.g. the

root of a tree, or are designated by an engineer.

In large feature models, the manual allocation of

weights is not tenable and an agreed algorithm for the

automatic allocation of weights needs to be

established. We do not address this issue in this paper.

Degree Centrality: The connection strength of a

feature F can be formed by calculating the degree of

each feature (vertex) on a graph i.e. the sum of the

Evaluating the Relative Importance of Product Line Features Using Centrality Metrics

471

total number of edges going into the feature (in-

degree) and the total number of edges coming out of

the feature (out-degree). Eq. (1) shows that for an

undirected graph, the Degree Centrality (DC) of a

feature F is the sum of the connection strengths FG

for each F directly connected to a feature G

(i.e. “one-

hop”) where D

is the total number of connections to

feature F. Normalisation between 0 and 1 is achieved

through division by (N-1) where N is the total number

of features in the graph.

DC (F)= (Σ FG

) / (N-1)

(1)

i=0

Closeness Centrality: The overall connection

strength of a feature F can be formed by calculating

the average shortest distance from each feature to

every other feature G

where N is the total number of

features in the graph (Eq. 2). For undirected graphs

inward and outward edges are included in the

calculations. For directed graphs, only the out-degree

is included. If there is no (directed) path from F to G

then the distance is 0. If the sum of the distances for

a feature is small then its closeness is high. The higher

the closeness the quicker a feature can communicate

to other features across the graph. Closeness

Centrality can be a useful measure of identifying

global connectivity but in a highly connected

network, many features can have similar scores and

are less distinctive in their global relevance.

Closeness Centrality can also help with finding

influential features in an isolated large cluster.

CC (F) = 1 / (Σ FG

(avg shortest path distance)) (2)

i=0

Eccentricity Centrality: The overall connection

strength of a feature F can be formed by calculating

the maximum distance (longest path) between the

feature and any other feature G

in the graph. Eq. 3

shows Eccentricity Centrality to be the inverse of the

maximum distance i.e. the shorter the distance the

greater the relative importance. Eccentricity can be a

useful indicator of the absolute centrality of a feature

within a graph. For undirected graphs, inward and

outward edges are included in the calculations. For

directed graphs, only outward edges are included, and

if there is no outward edge e.g. on leaf features, then

the eccentricity score is 0.

EC (F) = 1 / Σ FG

(max distance) (3)

j= 0

Eigenvector Centrality: The overall connection

strength of a feature F can be formed by calculating if

it has an outgoing connection to features that in turn

have outgoing connections or if it has incoming

connections from features that themselves have

incoming connections. Eq. (4) shows that the

Eigenvector Centrality of F connected to G

is a

function of the eigenvector centralities of the features

that G

is connected to. For undirected graphs inward

and outward edges are included in the calculations.

For directed graphs, only outward edges are included.

Eigenvector centrality can be a useful measure of

global relevance. For directed graphs, a feature’s

importance derives from the centrality of the features

that point to it; for undirected graphs, a feature’s

importance combines the centrality of features that

point to it and those to which it points where

is the

set of features directly connected to F and where λ is

a constant.

EGC (F) = (1/λ) Σ EGC(G

) (4)

i=0

Between-ness Centrality: The overall connection

strength of a feature F can be formed by calculating

the number of times it lies on one of the shortest paths

between two other features P

and Q

(Eq. 5). For

undirected graphs inward and outward edges are

included in the calculations. For directed graphs, only

the out-degree is included. Features with high

between-ness centrality are important because they

typically connect different groups of features.

Features with a low between-ness centrality are less

important and are often located at the periphery of a

network. To normalize the value between 0 and 1

divide by (N-1)(N-2) where N is the total number of

features in the graph. For directed graphs divide by

(N-1)(N-2)/2.

BC (F) = Σ No. shortest paths in P

going through F (5)

i,j, i≠j

No. of shortest paths in P

Table 2 summarises the Centrality Metrics used

Table 2: Summary of Centrality Metrics.

Metric Benefits

Degree

Centrality

a measure of a feature’s local connectivity

(“one-hop” connections)

Closeness

Centrality

a measure of how quickly a feature can

communicate to other features across the

graph

–

the closer the bette

Eccentricity

Centrality

a measure of a feature’s distance to the absolute

centre point of the graph

Eigenvector

Centrality

a measure of a feature’s connectivity to other

important features

Between-ness

Centrality

a measure of a feature’s connectivity to

disparate groups of features

The metrics in Eqs. (1-5) assume that the connection

strength value (“weight”) of the connecting edge

between features is the same throughout the network

and equal to 1, effectively “unweighted”.

ICSOFT 2024 - 19th International Conference on Software Technologies

472

5 GSMA MODEL

Using the GSMA feature model we calculated values

for each of the five centrality metrics in Section 3.

Table 3 and 4 show the top 10 ranked features for

each centrality metric when considering the feature

model as an unweighted undirected graph. and an

unweighted directed graph.

Full tables are available at:

https://figshare.com/s/

1475000bed40c6f7bc56.

Table 3: Centrality Metrics for Feature Model as an

Unweighted Undirected Graph.

Unweighted Undirected Graph

Feature Rank DC CC EC EGC BC

1 82 15 0 16 15

2 16 0 15 15 0

3 36 77 77 82 77

4 30 16 1 0 82

5 47 30 6 30 47

6 53 47 12 77 30

7 0 6 70 47 16

8 6 12 16 26 53

9 15 65 30 27 36

10 77 68 47 28 70

Table 4: Centrality Metrics for Feature Model as an

Unweighted Directed Graph.

Directed Graph

Feature Rank DC CC EC EGC BC

1 82 1 2 21 15

2 16 6 3 24 82

3 36 12 4 38 47

4 30 17 5 39 53

5 47 20 7 45 30

6 53 23 8 55 36

7 0 26 9 56 16

8 6 27 10 58 77

9 15 28 11 59 89

10 77 37 13 60 95

When comparing metrics on the same graph, the

feature rank is more helpful than the absolute value

because the calculations are different. Absolute

values can be helpful when comparing the structure

of two different graphs with the same metric (using

normalised values between 0 and 1). Table 5a and 6b

show the frequency with which a feature appears in

the Top 10 rankings in Table 3 e.g. in Table 3 Feature

15 appears in the Top 10 for all five metrics.

For the unweighted undirected graph, the most

prominent six features that appear in each metric list

are: Features, 0, 15, 16, 30, 47, 77. Appendix 1 shows

these features occupy prominent roles in the upper

echelons of the model. Interestingly, Features 16, 30

and 47 are all Optional which raises the question of

whether they actually should be Optional. In other

cases, where a feature appears in the Top 10 of only

one metric, consideration might be given to whether

these features are connected appropriately within the

model. For example, consider Features 26 and 27

concerning device unlocking and application login,

respectively. Given that access to many functions is

dependent on if a device is locked or not and whether

a user is logged in or not, one might review if these

features should be situated higher up the model.

Table 5: Frequency of Top Features in Centrality Metrics

for Unweighted Graphs (a) Undirected (b) Directed.

Undirected (Table 3) Directed (Table 4)

Feature Top 10

Ranking

Frequency

Feature

Top 10

Ranking

Frequency

0 5 6 2

15 5 16 2

16 5 36* 2

30 5 47 2

47 5 53 2

77 5 77 2

6 4 82 2

82 3 89* 2

12,36,53,70 2 95* 2

*These 3 features also share the highest value for Closeness Centrality

with 16 other features so arguably are slightly more important.

For the unweighted directed graph, several

prominent features are also prominent in the

undirected graph i.e. Features 6, 16, 36, 47, 77, 82,

but their Top 10 ranking frequency is lower, which

seems to be less helpful. Similarly, Feature 15, which

appears prominently in the undirected graph, does not

appear in the directed graph principally because it is

not in the top 10 rankings for the closeness,

eccentricity or eigenvector metrics. However,

representing a feature model as a directed graph helps

identify “root nodes” and “leaf nodes”. Root nodes

have only outward connections i.e. their in-degree

value is 0. Leaf nodes have only inward connections

i.e. their out-degree is 0, and the closeness, between-

ness and eigenvector centrality metrics will be 0.

6 DISCUSSION AND THREATS

TO VALIDITY

Product line feature models evolve over time and can

include changes to their topology and to each

feature’s properties and its relative importance.

Relative importance metrics offer clues to where

significant impacts might occur as a model evolves

and are computationally straightforward.

Any analysis of a feature model using metrics

requires the normal degree of caution and prudence

about relying on any one metric. A single individual

metric is likely to be of greater value to managers and

Evaluating the Relative Importance of Product Line Features Using Centrality Metrics

473

engineers when it is placed against other sources of

evidence. The practices of reflection, relying on

intuition and any visual inspection of the graphical

version of a feature model, if available and practical,

remain valuable methods to deploy alongside metrics.

Relative Importance here refers only to a feature’s

prominence within the model and may be affected by

other perspectives of the supplier or a customer,

captured in a feature’s semantic properties. Future

work might explore the value of other centrality

metrics as well as combining them with semantic

property values. The usefulness of a metric is often

determined by the running time of the algorithm that

implements it. We did not explore the running times

of each of these metrics on very large feature models.

Allocating weights to features and edges in a

feature model can offer additional insight into the

relationships between features. In large feature

models, weights allocation is untenable without the

use of an automated algorithm. We did not address

automatic weight allocation in this paper. Future

work might also consider whether weights should be

adapted to reflect different influences that features

might have on one another when models are

scrutinised for different purposes e.g. examining the

impact of proposed changes on different customers,

exploring design or implementation considerations,

or considering outsourcing arrangements.

We used the open-source tool Gephi version

0.10.1 (Gephi, 2024). We observed that the

calculation for degree centrality includes both inward

and outward edges whether the graph is directed or

undirected. However, when calculating the other four

metrics in a directed graph, Gephi only includes

outward edges. We also noted that if there are weights

attached to edges, Gephi includes these in its

calculations for degree centrality, but ignores them

for the other four metrics. We have not explored how

other tools behave.

7 RELATED WORK

Many graph metrics have been proposed to identify

important vertices in a graph, across many different

fields. Selecting the most suitable for specific

applications remains a challenge. To address this

problem a culling method is proposed (Chebotarev et

2003) that involves forming a set of candidate

measures, generating the minimum number of graphs

needed to distinguish each measure, constructing a

decision-tree survey for experts, and identifying the

measure consistent with the expert’s view.

Centrality metrics have been investigated for

diverse applications. For internet topology analysis,

(Wills et al, 2020) made a comparison of commonly

used graph metrics and distance measures to discern

between common topological features found in both

random graph models and real-world networks. They

proposed a multi-scale picture of a graph structure to

study the effect of global and local structures on

changes in distance measures. In (Wan et al, 2011) a

small number of centrality metrics are discussed in

their application and performance for solving various

computing and engineering problems in networks

based on extensive simulation experiments. A com-

parative overview of metrics for evaluating network

robustness is presented in (Oehlers et al, 2021). Other

applications include mobile social network applica-

tions (Zhou et al, 2018), visual reasoning in online

social networks (Correa et al, 2012), water distribu-

tion networks (Narayanan et al, 2014) and traffic

management for space satellite networks (Zhang et al,

2018). (Jirapanthong 2012) proposed the use of a

social network to represent software product line

artefacts and relationships between those artefacts to

apply centrality metrics for analysing the dependen-

cies between software artefacts and stakeholders to

improve software processes.

(Bagheri et al, 2011) showed that structural met-

rics in an SPLE feature model can be used to predict

its maintainability. Thresholds for implementation

metrics were examined in (Vale at al 2015). In

(Bagheri et al, 2010) a Stratified Analytic Hierarchy

Process (S-AHP) method is presented for prioritizing

(ranking) and filtering the features based on the judg-

ments of users of a product line, to enhance and ex-

pedite the feature selection and product configuration

process. An algorithm was described in (Peng et al,

2016) to identify the relative importance of a feature

in a feature model assumed to be a directed acyclic

weighted graph. Relative importance was calculated

as a function of weighted degree centrality i.e. the

weighted in-degree divided by the weighted out-de-

gree. The weight values allocated were 1 to manda-

tory, 0.5 to optional, 1/N for XOR where N is the total

number of features that are mutually exclusive and for

I-OR the weight is some value between 1/N and 1

where N is the total number of features that can be

included. Another approach to weight allocation was

presented in (Mannion et al, 2023), where features

were allocated weights based on their variability type

and where the calculations relied on designated start

and end vertices i.e. a directed graph was assumed.

In object-oriented software engineering, the

connections between classes and objects can be used

to build a dependency graph of classes from which

ICSOFT 2024 - 19th International Conference on Software Technologies

474

centrality measures can be extracted. This type of

graph was used in (Ouellet et al, 2023) to show that

using centrality measures in combination with object-

oriented metrics can improve the prediction of fault-

prone classes as well as the prediction of the number

of faults in a class. Centrality measures when

combined with object-oriented metrics can also be

shown (Levasseur et al, 2024) to better predict the

unit testing effort and help prioritize unit tests.

8 CONCLUSION

During product line feature model analysis, the more

important a feature, the more attention it receives and

the more influence it has on the analysis outcome.

Over time, as a product line evolves, features’ relative

importance values change and need to be

recalculated. We show how a small number of

centrality metrics drawn from social network analysis

can be used to establish a feature’s relative

importance for feature model analysis. The metrics

selected were: degree centrality, closeness centrality,

eccentricity centrality, eigenvector centrality and

between-ness centrality. The metrics provide some

insight into a feature’s contribution to a model’s

cohesiveness and the information flows between

features. We acknowledge that a feature’s relative

importance refers here only to its structural

prominence within a feature model and does not

include its value from other perspectives. We

recommended comparing how a feature ranks across

several metrics rather than just one metric.

REFERENCES

Bagheri, E., Gasevic, Assessing the Maintainability of

Software Product Line Feature Models using Structural

Metrics D., Software Qual J (2011) 19:579–612.

Bagheri, E., Asadi, M., Gasevic, D., Soltani, S. (2010).

Stratified Analytic Hierarchy Process: Prioritization

and Selection of Software Features, Proceedings of

14th Int’l Conference on Software Product Lines, SPLC

2010, LNCS 6287, J. Bosch and J. Lee (Eds.), 300–315.

Benavides, D., Sergio, S., Ruiz-Cortés, A. (2010).

Automated Analysis of Feature Models 20 Years Later:

A Literature Review, Information Sys, 35, 6, 615-636.

Bradner, S. (1997). Key words for use in RFCs to Indicate

Requirement Levels. See http://www.ietf.org/rfc

/rfc2119.txt (accessed 27/4/24)

BS ISO/IEC 26558:2017 (2017). Software and Systems

Engineering. Methods and Tools for Variability

Modelling in Software and Systems Product Line.

Chebotarev, P. Gubanov, D: How to Choose the Most

Appropriate Centrality Measure? A Decision Tree

Approach, https://arxiv.org/abs/2003.01052 (accessed

27/4/24)

C. Correa, T. Crnovrsanin, and K. Ma. (2012). Visual

Reasoning About Social Networks Using Centrality

Sensitivity. IEEE Transactions on Visualization and

Computer Graphics 18, 1 (Jan. 2012), 106–120.

Gephi, https://gephi.org/ (accessed 27/4/24)

Global Systems for Mobile communications Association

(GSMA), (2023). AI Mobile Device Requirements

Specification Version 2.0, https://www.gsma.com/new

sroom/wp-content/uploads//TS.47-v2.0.pdf (accessed

27/4/24)

Jirapanthong, W. (2012). Using Social Network Analysis

Technique for supporting Software Product Line

Process, Proc 2012 IEEE Int’l Conf. on Computer

Science and Automation Engineering, 344-348.

Knüppel, T., Thüm, S.. Mennicke, J.. Meinicke, J.,

Schaefer, I. (2017). Is There a Mismatch between Real-

World Feature Models and Product-Line Research,

ESEC/FSE’17, Sept 4-8, Paderborn, Germany, 291-302.

Lee, K., Kang, K.C., Lee, J. (2002). Concepts and

Guidelines of Feature Modeling for Product Line

Software Engineering, in Proceedings of International

Conference on Software Reuse, ICSR 2002:Software

Reuse: Methods, Techniques, and Tools, 62–77.

Levasseur, M-A., Mourad, B. (2024). Prioritizing unit tests

using object-oriented metrics, centrality measures, and

machine learning algorithms, Innovations in Systems

and Software Engineering, https://doi.org/10.1007

/s11334-024-00550-9.

Mannion, M., Kaind, H. (2023). Using Binary Strings for

Comparing Products from Software-Intensive Systems

Product Lines. In: Proceedings of 2023 IEEE 47th

Annual Computers, Software, and Applications

Conference (COMPSAC), Torino, 1638-1645.

Narayanan, I. Vasan, A., Sarangan, V., Kadengal, J.,

Sivasubramaniam, A. (2014). Little Knowledge Isn’t

Always Dangerous–Understanding Water Distribution

Networks Using Centrality Metrics. IEEE Transactions

on Emerging Topics in Computing, 2, 2, 225–238.

Oehlers, M., Fabian, B., (2021). Graph Metrics for Network

Robustness—A Survey

. Mathematics, 9(8), 895.

Ouellet, A., Mourad, B. (2024). Combining Object‐

Oriented Metrics and Centrality Measures to Predict

Faults in Object‐Oriented Software: An Empirical

Validation, Journal of Software Evolution and Process,

36, 4, April, e2548

Peng, Z., Wang, J., He, K., Li ,H. (2016). An Approach for

Prioritizing Software Features Based on Node

Centrality in Probability Network, Proc of the 15th Int’l

Conf on Software Reuse, ICSR 2016, Kapitsaki, G.M.,

Santana de Almeida, E (Eds.), 106–121.

Pure Systems, https://www.pure-systems.com/purevariants

(accessed 27/4/24)

Scott, J. (2017). Social Network Analysis, 4th edition.

Vale, G., Albuquerque, D., Figueiredo, E., Garcia, A.

(2015) Defining Metric Thresholds for Software

Product Lines: A Comparative Study, Proc of 19

Int’l

Conf on Software Product Lines, SPLC 2015, 176-185.

Evaluating the Relative Importance of Product Line Features Using Centrality Metrics

475

Wan, Z., Mahajan, Y., Kang, B.W., Moore, T.J., Cho, J-H.,

A Survey on Centrality Metrics and Their Implications

in Network Resilience, https://arxiv.org/pdf/2011.14

575.pdf (accessed 27/4/24)

Wills, P. Meyer, F., Chen, P-Y. (2020). Metrics for Graph

Comparison: A Practitioner's Guide, PloS one, 15, 2,

p.e0228728-e0228728

Zhang, Z., Jiang, C., Guo, G., Qian, Y. and Y. Ren. (2018).

Temporal Centrality-balanced Traffic Management for

Space Satellite networks. IEEE Transactions on

Vehicular Technology 67, 5, 4427–4439.

Zhou, H., Ruan, M., Zhu, C., Leung, V,. Xu, S., Huang. C.

(2018). A Time-ordered Aggregation Model-based

Centrality Metric for Mobile Social Networks. IEEE

Access 6, 25588–25599.

APPENDIX

GSMA Mobile Phone Specification

Mandatory Inclusive_OR Exclusive-OR

Optional

ICSOFT 2024 - 19th International Conference on Software Technologies

476