Local Differential Privacy for Data Clustering

Lisa Bruder

and Mina Alishahi

Informatics Institute, University of Amsterdam, The Netherlands

Department of Computer Science, Open Universiteit, The Netherlands

Keywords:

Local Differential Privacy, Clustering, Privacy, Non-Interactive LDP.

Abstract:

This study presents an innovative framework that utilizes Local Differential Privacy (LDP) to address the

challenge of data privacy in practical applications of data clustering. Our framework is designed to prioritize

the protection of individual data privacy by empowering users to proactively safeguard their information before

it is shared to any third party. Through a series of experiments, we demonstrate the effectiveness of our

approach in preserving data privacy while simultaneously facilitating insightful clustering analysis.

1 INTRODUCTION

The widespread use of digital technology has led to a

massive amount of data being available, bringing with

it a signiﬁcant responsibility to handle this data care-

fully. While data collection for statistical purposes

is not new, the exponential growth in data volume

coupled with the escalating threat of data breaches

has intensiﬁed concerns regarding the conﬁdentiality

of sensitive information in recent years (Seh et al.,

2020). Data breaches have highlighted the risks asso-

ciated with unauthorized access to user data, raising

awareness about the potential consequences of such

breaches on individuals and organizations. Conse-

quently, there is a growing demand to develop ro-

bust solutions to safeguard sensitive data and protect

user privacy (Kasiviswanathan et al., 2011) (Xia et al.,

2020).

One such task in data analysis is data clustering,

which falls within the realm of unsupervised learning

methods wherein patterns are discerned from unla-

beled data points. The primary objective of data clus-

tering is to unveil underlying patterns within a dataset

by grouping data points into distinct clusters (Xu and

Tian, 2015). However, given that data clustering often

involves accessing sensitive user information, ensur-

ing the protection of users’ privacy is paramount.

Although numerous methods in the literature have

been proposed to address the challenges of privacy-

preserving clustering, these proposed solutions often

fail to meet the following conditions:

• Lack of Individual Privacy Protection: Existing

solutions often fail to protect single individual pri-

vacy locally on users’ devices, necessitating trust

in third-party entities, such as Differential Privacy

in private clustering (Li et al., 2024).

• Interactive Approach: In cases where individual

privacy is preserved, the proposed methods typi-

cally require continuous user involvement in train-

ing the clustering algorithm (Yuan et al., 2023)(He

et al., 2024).

• Narrow focus: Many solutions are tailored for

speciﬁc use cases, limiting their applicability to

speciﬁc clustering training, such as exclusively

for K-means clustering (Hamidi et al., 2018).

• Computational Overhead or Loss of Utility:

These solutions may entail computationally in-

tensive processes, such as encryption techniques

(Sheikhalishahi and Martinelli, 2017b), or lead to

a loss of utility, such as through anonymization

methods (Sheikhalishahi and Martinelli, 2017a).

To overcome the mentioned constraints, our study in-

troduces a novel framework leveraging Local Differ-

ential Privacy (LDP), wherein individual users protect

their information by perturbing their data locally on

their devices before sharing it with a third party, such

as an aggregator (Alishahi et al., 2022). The aim of

perturbation is to ensure that the estimation expecta-

tion remains unbiased and to minimize statistical vari-

ance as much as possible. Speciﬁcally, we employ

an LDP-based frequency estimation technique, a fun-

damental statistical objective under local differential

privacy protection.

To explore the effectiveness of LDP-based fre-

quency estimation for private clustering, we conduct

820

Bruder, L. and Alishahi, M.

Local Differential Privacy for Data Clustering.

DOI: 10.5220/0012838800003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 820-825

ISBN: 978-989-758-709-2; ISSN: 2184-7711

a series of experiments. These experiments focus on

investigating the impact of key parameters, including

the number of cells used for discretization, the size

of the input dataset, and the privacy budget. By sys-

tematically varying these parameters, we aim to gain

insights into their inﬂuence on the LDP-based clus-

tering process and assess the performance of our ap-

proach under different settings.

2 PRELIMINARIES

This section presents clustering and local differential

privacy as preliminary concepts employed in our pro-

posed framework.

k-means Clustering: is a method for partitioning

a dataset into k clusters based on similarity. It it-

eratively assigns data points to the nearest cluster

centroid and updates centroids to minimize intra-

cluster variance. Formally, given a dataset X consist-

ing of n data points {x

,... ,x

} and the desired

number of clusters k, the K-means clustering algo-

rithm aims to partition the data into K clusters, C =

,. .. ,C

}, such that it minimizes the within-

cluster sum of squares (WCSS).

Local Differential Privacy (DP): is a privacy-

preserving mechanism in which an aggregator gathers

information from users who has some level of distrust

but are still willing to engage in the aggregator’s anal-

ysis.

Formally, a randomized mechanism M adheres to

ε-LDP if and only if, for any pair of input values v,v

′

∈

D and for any possible output S ⊆ Range(M ), the

following inequality holds:

Pr[M (v) ∈ S] ≤ e

Pr[M (v

′

) ∈ S] (1)

when ε is understood from the context, we refer to

ε-LDP simply as LDP.

Randomized Aggregatable Privacy-Preserving

Ordinal Response (RAPPOR) (Erlingsson et al.,

2014): introduced by Google, is a hash-based

frequency statistical method that randomly selects

a hash function H from a hash function family

H = {H

,. .. ,H

}, where each function outputs

an integer in [k] = {0, 1,. .. ,k − 1}. RAPPOR then

encodes the hash value H (v) as a k-bit binary vector

and randomized response is performed on each bit.

Accordingly, the encoded vector v

is shaped as

follows:

[i] =

(

1 i f H (v) = 1

0 otherwise

(2)

Figure 1: Server side.

The encoded vector is then perturbed as:

Pr[ ˆv

[i] = 1] =

(

1 −

f i f v

[i] = 1

f i f v

[i] = 0

(3)

where f = 2/(e

+1). The aggregator employs Lasso

regression to improve the estimated frequency value

out of collected reports.

3 METHODOLOGY

Our approach is constituted of the following steps as

shown in Figures 1 and 2:

Discretization (Shaping the Cells): In this critical

phase, the aggregator employs domain knowledge re-

garding feature ranges to discretize the dataset, thus

delineating cells to accommodate data points falling

within these ranges. The process entails setting inter-

vals by uniformly partitioning the anticipated range

of continuous values present in the dataset. For in-

stance, in the context of adult height values expected

to range between 1.4 and 2.0 meters, the process

may involve dividing this range uniformly into three

intervals, yielding non-overlapping boundaries such

as [1.4,1.6), [1.6, 1.8), and [1.8,2.0]. Each interval

demarcates a cell boundary, determining where data

points align in relation to these boundaries. Con-

sequently, data points are assigned to speciﬁc cells

based on their relative positioning within these inter-

vals. This process serves as a foundational step in

subsequent aggregation and analysis tasks, enabling

effective handling of continuous data.

The aggregator assigns integer identiﬁers to each

cell, and subsequently discloses both the boundaries

of these cells and their respective identiﬁers to users.

LDP-Based Frequency Estimation: LDP-based fre-

quency estimation offers a means for the aggregator

to approximate the count of individuals within spe-

ciﬁc cells, all while maintaining user privacy regard-

ing their cell associations. Users start by pinpoint-

ing the cell where their data resides and extracting its

corresponding integer identiﬁer. Through the LDP-

based frequency estimation algorithm, users perturb

their answer by an alternative integer identiﬁer (out

of the list of existing identiﬁers). This method ensures

that individual contributions remain conﬁdential, yet

Local Differential Privacy for Data Clustering

821

Figure 2: Client-side (top) and Server-Side Architecture (bottom).

still allows for reliable estimation of aggregate fre-

quencies within cells. In this study, we utilize RAP-

POR as the chosen LDP-based frequency estimation

protocol due to its demonstrated accuracy in this con-

text. Nonetheless, our proposed framework is ﬂexi-

ble and can accommodate any alternative LDP-based

frequency estimation technique, providing versatility

and adaptability to different privacy requirements and

data characteristics.

Generating New Dataset: The aggregator gathers

cell identiﬁers submitted by users and then associates

a new data point with each user based on this infor-

mation. Speciﬁcally, if a user reports that their data

point d belongs to cell c

∗

, the aggregator assigns a

new point, denoted as d

, randomly within this iden-

tiﬁed cell. This process ensures that each user’s re-

ported data point is mapped to a representative point

within the corresponding cell.

Clustering: Now, armed with the newly generated

dataset, the aggregator proceeds to train a cluster-

ing algorithm. This algorithm’s structure can subse-

quently be shared with any third party for their use.

Our proposed approach offers ﬂexibility by remain-

ing agnostic to the choice of clustering algorithm. In

this particular study, we opt for the widely used k-

means clustering method. This selection, however,

does not constrain the applicability of our approach,

as it can seamlessly integrate with various cluster-

ing techniques depending on speciﬁc analysis require-

ments and preferences.

Theorem 1 As the number of cells and privacy bud-

get ε increase, the error of ε-LDP frequency esti-

mation techniques, such as RAPPOR, also increases.

Conversely, increasing the number of data points re-

duces the error rate of these techniques.

Proof: This conclusion directly stems from the error

characteristics of frequency estimation techniques.

The Mean Squared Error bound of RAPPOR is ex-

pressed as Θ



−1



, where r denotes the num-

ber of cells and n represents the size of the dataset

(Wang et al., 2020). From this formula, it is evi-

dent that an increase in ε and r leads to a higher error

bound, while an increase in the number of users (data

points) decreases the error bound.

It is noteworthy that while we speciﬁcally discuss

the error bound of RAPPOR here, this argument holds

true for other frequency estimation protocols, such as

Hadamard and RR techniques (Wang et al., 2020).

Proposition 1 While increasing the number of cells

negatively impacts the accuracy of frequency estima-

tion techniques, it improves the accuracy of cluster-

ing algorithms trained on published data within our

methodology.

Proof: If the frequency estimation technique ade-

quately preserves the distribution of each cell, the size

of cells still affects the accuracy of clustering. This

is because if a cluster boundary intersects the mid-

dle of a cell, a larger cell size increases the risk of a

data point falling outside the cluster boundary when

the aggregator returns a randomized point based on

the shared cell identiﬁer. In contrast, smaller cells in-

crease the likelihood of cells aligning more closely

with cluster boundaries, thereby enhancing clustering

accuracy. This can be formulated as following:

argmin

∑

i=1

∑

x∈S

∥x−µ

∥

= argmin

∑

i=1

∑

x∈∆

∥x−µ

∥

where S

is the i’th cluster, and S

∑

∆

, for ∆

con-

sidered as the cells overlapping with cluster S

Proposition 2 Increasing the number of data points

and privacy budget improves the clustering accuracy.

Proof: The variations in the number of data points

and privacy budget do not directly inﬂuence the ac-

curacy of clustering. However, they indirectly im-

pact clustering accuracy through their effect on ac-

curate frequency estimation. Since clustering serves

as a post-processing step in our methodology, the im-

provements in frequency estimation resulting from an

increase in data points and privacy budget should also

lead to enhanced clustering accuracy.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

822

Figure 3: Original data points with 25 cell grid.

4 EXPERIMENTS

4.1 Experimental Set-Up

Experiment Environment: We program the code

for our experiments using the programming language

Python. We use the pure-ldp

package’s RAPPOR

client- and server-side implementation as well as

scikit-learn

for k-means clustering and matplotlib

to plot the data we gathered.

Dataset: For our experiments, we utilize the “Esti-

mation of obesity levels based on eating habits and

physical condition” dataset sourced from the UCI Ma-

chine Learning Repository

. This dataset encom-

passes health information gathered from individuals

in Mexico, Peru, and Colombia, supplemented with

synthetically generated data derived from the original

dataset. Its relevance to our research lies in its in-

clusion of sensitive health-related data, presenting a

realistic scenario where data privacy is of paramount

importance. The dataset contains 2111 records, and

it is described with 17 features. Out of the 17 fea-

tures available, we speciﬁcally focus on utilizing the

two continuous features, namely ’Age’ and ’Height’,

for visualization purposes. Additionally, we set aside

20% of our original data for future evaluation, pre-

serving these data points to assess the accuracy of our

newly developed model.

Discretization: We discretize the values into uniform

cells, ranging from 1.4 to 2.0 meters for height and

10 to 70 years for age, based on the feature value

ranges. Each discretized value is then assigned an in-

teger identiﬁer corresponding to the cell it falls into.

For example, a data point with a discretized age value

of “1” (age in the interval [22, 34)) and a discretized

height value of “2” (height in the interval [1.64, 1.76))

would be associated with the cell “12”. Figure 3

shows how the cells are shaped on our original data.

https://pypi.org/project/pure-ldp/

https://pypi.org/project/scikit-learn/

https://pypi.org/project/matplotlib/

https://doi.org/10.24432/C5H31Z

Table 1: Parameters tuning.

Parameter Range of values

Number of cells 4 - 100

Fraction of data points 0.1 - 1.0

RAPPOR Epsilon 1, 2, 4, 8

Frequency Estimation: Upon determining the cell

identiﬁer where their data resides, each user employs

RAPPOR locally on their device to perturb the cell

number. For RAPPOR implementation, we adhere to

the defaults established by Google in their RAPPOR

demo: setting the bloom ﬁlter size to 16 and utilizing

2 hash functions.

Clustering: Initially, we randomly assign a new point

for each point that falls within a cell. Subsequently,

we train the k-means clustering algorithm on both the

original data and the data generated by RAPPOR. We

opt for k = 5, determined through the elbow technique

applied to the original dataset. It’s worth noting that

while k-means is an iterative clustering algorithm, this

iterative process occurs solely on the aggregator side,

with only interacting users once during the collection

of their perturbed data.

Evaluation Metric: To assess the efﬁcacy of our

LDP-based clustering approach, we conduct a com-

parison of labelings between the 20% reserved orig-

inal data and the RAPPOR-generated data. Firstly,

we determine centroids for both datasets through k-

means clustering. Each data point is then assigned

to the nearest centroid, allowing us to evaluate the

consistency of labels. We measure the accuracy by

calculating the percentage of data points accurately

labeled. This is achieved by dividing the number of

data points labeled the same between the original and

RAPPOR-generated data by the total number of data

points used for prediction. The resulting percentage

represents our utility metric. A higher percentage

indicates a closer alignment between the RAPPOR-

based model and the original dataset.

Parameter Tuning: To evaluate the effects of various

parameters within our framework, we explore differ-

ent values for the number of cells, fraction of dataset

used as input source, and privacy budgets. The range

of parameters varied for our experiments is summa-

rized in Table 1. It is noteworthy that while one pa-

rameter varies, the other two parameters remain ﬁxed.

For enhanced reliability, we repeat our experiments

50 times and report the average results.

4.2 Results

The Inﬂuence of Cell Count and privacy Budget:

Our initial experiments aims to investigate the inﬂu-

ence of cell count and privacy budget on accuracy. We

Local Differential Privacy for Data Clustering

823

tested cell counts ranging from 4 to 100 cells, specif-

ically focusing on square numbers within this range.

Figure 4a shows the outcome of this experiment for

four different epsilon values 1, 2, 4, and 8. The trend

reveals that smaller cell sizes, corresponding to higher

cell counts, generally result in greater accuracy across

all epsilon values up to 81 cell counts. This observa-

tion underscores the existence of a trade-off associ-

ated with the number of cells, where simply increas-

ing cell counts does not guarantee accuracy enhance-

ment. This observation resonates with the ﬁndings of

our theoretical analysis. The variation of privacy bud-

get does not show a signiﬁcant change in accuracy.

This can be resulted from the distribution of data un-

der analysis. In other words, even the higher random-

ness noise still keeps the structure of data properly

for clustering. It of course needs more investigation

in future studies for variety of datasets. This outcome

speciﬁcally suggests the use of lower epsilon values

(higher privacy gain) in our methodology. To gain a

better insight on the dispersion of accuracy on 50 runs

of experiments, we depict this variance in Figure 4b

for epsilon 1 and different cell counts. It can be seen

that the widest range of values is observed with 64

cells, where accuracy spans from a minimum of 18%

to a maximum of 90%, reﬂecting a variance of 72%.

While this dispersion is unavoidable due to the ran-

domness inherent property of LDP, it can be seen that

yet increasing the number of cell counts leads to the

improvement in accuracy.

The Inﬂuence of Dataset Size: Figure 6 shows the

impact of dataset size by considering fractions of data

on the accuracy of our methodology. For this dataset,

the amount of data points in the data set does not

seem to consistently inﬂuence the accuracy we can

achieve using RAPPOR. The values stay pretty con-

sistent across all data set sizes and there is no consis-

tent trend. The chosen Epsilon value does not seem to

have much inﬂuence on the accuracy either. This can

be resulted from the distribution of our dataset and the

precision of RAPPOR in preserving the distribution

of data even in smaller sizes.

Once again, Figure 6 reveals a notable disparity

among accuracy values across experiment runs. Some

runs exhibit considerably low accuracy rates, while

others nearly achieve 100%. Particularly intriguing is

the scenario involving the smallest dataset size, com-

prising only a fraction of 0.1 relative to the original

dataset size. Here, the attained accuracy spans from a

minimum of 14% to a maximum of 95%. Despite this

variance, computing the median accuracy across all

experiment runs still yields commendable results. In-

terestingly, the dataset sample size of 0.9 of the origi-

nal dataset demonstrates the least dispersion, with ac-

curacy ranging from 62% to 96%.

Discussion. We present the guidelines for using our

framework, our experimental ﬁndings, and our plan

for future directions.

• We have assumed that the features are continuous.

However, our methodology can also be applied on

discrete features. To this end, it is enough that we

use the boundary of cells as shared value and as

randomized value by the aggregator.

• We found that the number of cells has impact on

the accuracy of our methodology both in negative

and positive way. There is a trade-off in the num-

ber of cells for each dataset that the accuracy is

optimized. However, it should be noted that the

aggregator has no knowledge about the data to of-

fer the optimum number of cells in advance. To

this end, in the future directions, we plan to de-

sign a privacy-preserving mechanism to infer the

optimum number of cells without accessing the

original data.

• Although our experiments did not show a con-

siderable impact of dataset size on accuracy, we

believe that this requires more extensive exper-

iments when also the dataset distribution also

comes under consideration. Given the inherent

property of LDP mechanism, we expect that the

size of dataset single alone might night affect the

outcome if the dataset if the data is almost well

evenly distributed across all cells.

• We found the optimum number of clusters using

elbow technique on original datset. This is some-

thing that the aggregator does not know without

accessing the original data. In future direction,

we plan to investigate the impact of the number of

clusters on accuracy.

5 CONCLUSION

This study introduces a novel framework that lever-

ages Local Differential Privacy (LDP) to safeguard

individual data privacy, empowering users to take

proactive measures to protect their information be-

fore any sharing occurs with third parties in a non-

interactive engagement of users. Through a compre-

hensive series of experiments, we provide compelling

evidence of the efﬁcacy of our approach in preserv-

ing data privacy while also enabling meaningful and

insightful clustering analysis.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

824

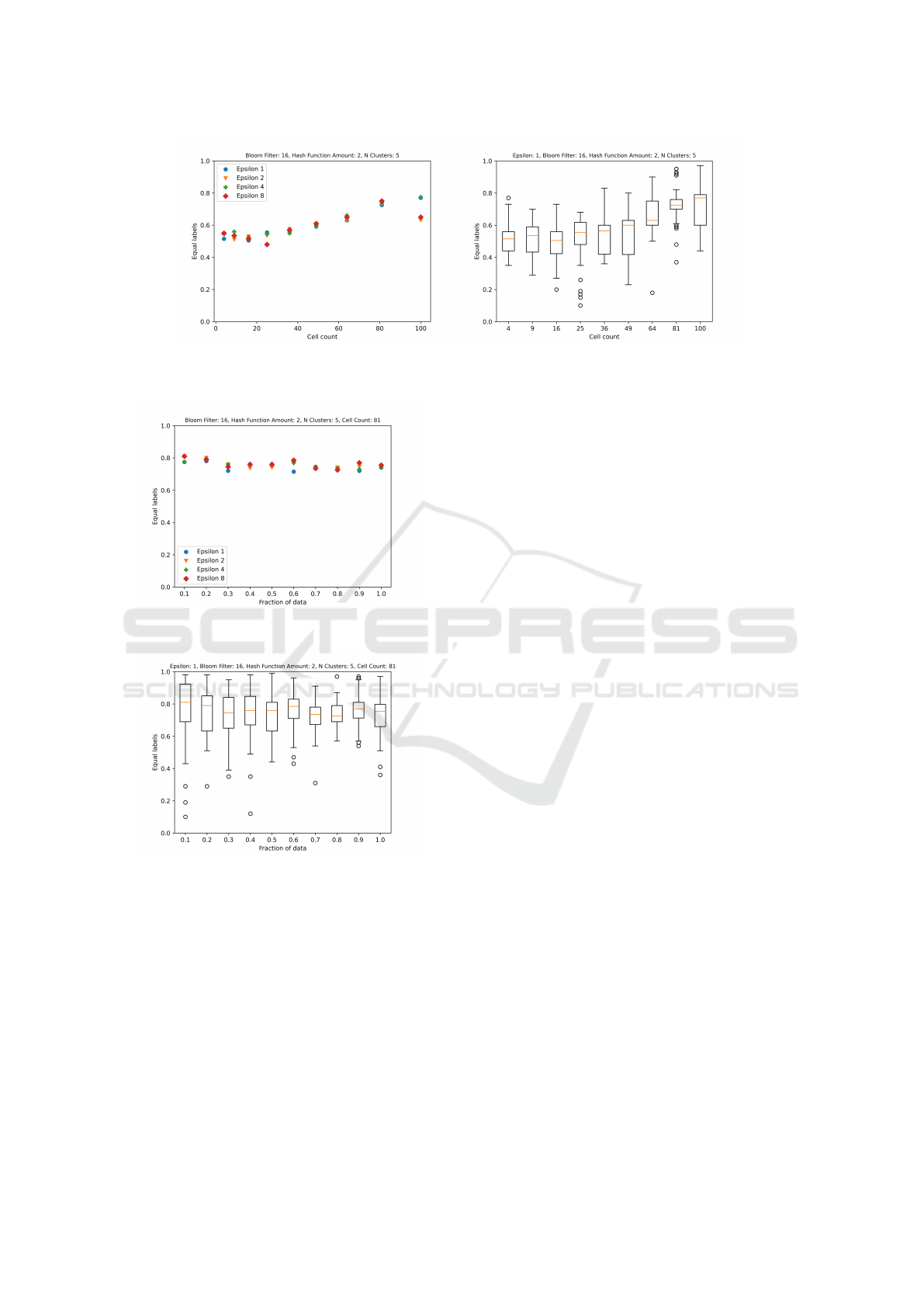
(a) Varying cell counts over 50 runs. (b) Box plot for epsilon 1.

Figure 4: The impact of cell counts and privacy budget.

Figure 5: Varying dataset size for Epsilon 1, 2, 4, 8 with

median accuracy over 50 runs.

Figure 6: Epsilon 1 box plot based on all 50 accuracy val-

ues.

REFERENCES

Alishahi, M., Moghtadaiee, V., and Navidan, H. (2022).

Add noise to remove noise: Local differential privacy

for feature selection. Comput. Secur., 123:102934.

Erlingsson,

U., Pihur, V., and Korolova, A. (2014). Rappor:

Randomized aggregatable privacy-preserving ordinal

response. In Proceedings of the 2014 ACM SIGSAC

conference on computer and communications secu-

rity, pages 1054–1067.

Hamidi, M., Sheikhalishahi, M., and Martinelli, F. (2018).

Privacy preserving expectation maximization (EM)

clustering construction. In DCAI conference, volume

800 of Advances in Intelligent Systems and Comput-

ing, pages 255–263. Springer.

He, Z., Wang, L., and Cai, Z. (2024). Clustered feder-

ated learning with adaptive local differential privacy

on heterogeneous iot data. IEEE Internet of Things

Journal, 11(1):137–146.

Kasiviswanathan, S. P., Lee, H. K., Nissim, K., Raskhod-

nikova, S., and Smith, A. (2011). What can we learn

privately? SIAM Journal on Computing, 40(3):793–

826.

Li, Y., Wang, S., Chi, C.-Y., and Quek, T. Q. S.

(2024). Differentially private federated clustering

over non-iid data. IEEE Internet of Things Journal,

11(4):6705–6721.

Seh, A. H., Zarour, M., Alenezi, M., Sarkar, A. K., Agrawal,

A., Kumar, R., and Ahmad Khan, R. (2020). Health-

care data breaches: Insights and implications. Health-

care, 8(2).

Sheikhalishahi, M. and Martinelli, F. (2017a). Privacy pre-

serving clustering over horizontal and vertical parti-

tioned data. In IEEE Symposium on Computers and

Communications (ISCC), pages 1237–1244.

Sheikhalishahi, M. and Martinelli, F. (2017b). Privacy pre-

serving hierarchical clustering over multi-party data

distribution. In Security, Privacy, and Anonymity in

Computation, Communication, and Storage, volume

10656 of Lecture Notes in Computer Science, pages

530–544. Springer.

Wang, S., Qian, Y., Du, J., Yang, W., Huang, L., and Xu, H.

(2020). Set-valued data publication with local privacy:

tight error bounds and efﬁcient mechanisms. Proc.

VLDB Endow., 13(8):1234–1247.

Xia, C., Hua, J., Tong, W., and Zhong, S. (2020). Dis-

tributed k-means clustering guaranteeing local differ-

ential privacy. Computers & Security, 90:101699.

Xu, D. and Tian, Y. (2015). A comprehensive survey of

clustering algorithms. Annals of Data Science, 2:165–

193.

Yuan, L., Zhang, S., Zhu, G., and Alinani, K. (2023).

Privacy-preserving mechanism for mixed data cluster-

ing with local differential privacy. Concurr. Comput.

Pract. Exp., 35(19).

Local Differential Privacy for Data Clustering

825