Toward the Foundation of Digital Identity Theory
Pierre Fobougong Saha
1
, Mohamed Mejri
1
and Kamel Adi
2
1
Laval University, Qu
´
ebec, Canada
2
University of Quebec in Outaouais, Qu
´
ebec, Canada
Keywords:
Verifiable Credentials, Authentication, Privacy, Pruduct Family Algebra, Satisfiability Modulo Theories.
Abstract:
Verifiable Credentials (VC) have become today a de facto digital credentials standard and play an increasingly
important role in network exchanges. They often contain a large number of attributes that disclosure could have
unfortunate consequences. Formally verifying whether the user can access the requested service and ensuring
that their disclosed identity attributes generate the slightest risk, therefore, becomes very important. In this
paper, using the product family algebra, we show how the consideration of verifiable credentials can help to
easily and formally settle the question of whether a user can access a service and to respect the need-to-know
principle. To this end, we propose a translation of product family algebra into first-order Boolean logic and
vice versa. We then propose a Boolean equivalence of the product family algebra refinement operation. Using
all these tools, we show how the problem of verifying a user’s ability to authenticate, expressed using product
family algebra, easily translates into an SMT problem. In order to guarantee the preservation of privacy and
ensure the need-to-know principle, we associate VC attributes with a risk score and show how the question of
disclosing the attributes generating the least risk can easily be resolved with Maximum Weighted SMT. So we
can easily use the z3 solver to solve these problems in SMT form.
1 INTRODUCTION
In our daily life, we use various identity documents to
access services provided by different providers. This
may be a health insurance card, a national identity
card, a driving license, a study certificate, a diploma,
etc. The concept of verifiable credentials (VC) (Lim
et al., 2021; Xu et al., 2023; Li et al., 2022; Manu
et al., 2024), introduced by the W3C, tends to re-
produce these identity documents in a digital form
that can be easily stored in a digital wallet. Users,
therefore, are in possession of a large number of VCs
among which they must be able to prove their identity
to different service providers while running as little
risk as possible.
Although there is a growing body of scientific
work on the issue of privacy, very little of them ad-
dresses the need for a user-centric approach. How-
ever, it is clear that with the emergence of decen-
tralized technologies and self-sovereign identities, the
user plays a key role in data protection. Even if cryp-
tography, in particular zero-knowledge proof, have
become good tools for preserving privacy, the fact re-
mains that they are complex and cannot always prove
everything. In this research, we postulate that as-
signing risk scores to a user’s identity attributes can
enhance their privacy protection by disclosing only
those identity attributes necessary for accessing the
requested service. Additionally, this reinforces adher-
ence to the ’need-to-know’ principle from the user’s
perspective.
We show in this paper how the verification of a
user’s ability to access a service and the determina-
tion of attributes whose disclosure is likely to generate
the minimum risk can be easily solved using product
family algebra (PFA) (H
¨
ofner et al., 2011) and Sat-
isfiability Modulo Theories (SMT) (de Moura et al.,
2007) or Max weighted SMT.
1.1 Contributions
In this paper, we use of formal tools such as the prod-
uct family algebra and SMT (Satisfiability Modulo
Theories) to answer two essential questions in access-
ing online services: 1 - Can a user’s Verifiable Cre-
dentials be used to access a service ? 2 - What is
the subset of VCs attributes available to the user that
he can disclose while incurring the minimum risk ?
Thus, our main contributions are as follows:
• A translation of product family algebra into first-
order Boolean logic. Beyond helping us answer
812
Saha, P., Mejri, M. and Adi, K.
Toward the Foundation of Digital Identity Theory.
DOI: 10.5220/0012838100003767
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 812-819
ISBN: 978-989-758-709-2; ISSN: 2184-7711
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

the questions posed in this research, this transla-
tion can enable the rapid and reliable detection
of errors or conflicts in product configurations,
such as incompatible feature combinations or un-
fulfilled dependencies.
• A new methodological framework to enhance pri-
vacy and respect for the need-to-know principle in
a user-centric approach.
• A formal specification of the question of whether
a user can access a service and the set of attributes
whose disclosure generates the minimum risk and
the automatic resolution of these questions by the
Z3 SMT tool.
1.2 Outline
In Section 2, we briefly present Verifiable Creden-
tials, Product Family Algebra, Satisfiability Modulo
Theories (SMT) and the motivation behind this re-
search. Section 3 presents the proposed methodolog-
ical framework. Section 4 summarizes how we trans-
late the VC into a product family. Section 5 focuses
on defining the mathematical tools we intend to use in
our approach. Sections 6 and 7 deals with the imple-
mentation of our methodological framework. Section
8 summarises the existing literature on preserving pri-
vacy by taking risk into account in a user-centric ap-
proach. Finally, section 9 presents a discussion of our
results.
2 BACKGROUND AND
MOTIVATION
2.1 Verifiable Credentials and VC
Product Family
Verifiable credentials, as defined by the (Manu et al.,
2024), consist of tamper-evident claims about a sub-
ject made by an issuer. These credentials are piv-
otal for digital identity management and certification,
leveraging W3C standards, blockchain, and decen-
tralized identifiers (Manu et al., 2022). Issued by an
identity provider or self-generated, these credentials
are stored in a digital wallet, which can compile them
into verifiable presentations for submission to service
providers.
In this paper, we consider all VCs or VPs as prod-
uct families, akin to real-life identity documents. De-
spite variations in document type and issuing authori-
ties, common attributes like names and birth dates re-
main consistent for the same individual. Thus, multi-
ple identity documents share both commonalities and
variability, with each document regarded as a product
family.
2.2 Product Family Algebra (PFA)
Introduced by H
¨
ofner et al. (H
¨
ofner et al., 2011), a
product family algebra is a mathematical framework
based on idempotent semiring that provides a formal
way to represent and work with product families. This
algebraic structure allows for the expression of com-
mon concepts used in the product family paradigm,
such as how products are composed, the variability of
features, and the relationships between different prod-
uct families. For more information, we refer readers
to (H
¨
ofner et al., 2011).
Since verifying that a user can access a service re-
quires that he has the attributes required by the service
provider, we assume that if the user has a product fam-
ily VC and the service provider requires at least one
product from a product family R, then the chosen sub-
set of VC attributes contains all the attributes of some
products of R.
2.3 Satisfiability Modulo Theories
(SMT)
SMT solvers are pivotal in addressing verification
problems due to their capability to efficiently manage
complex logical constraints and theories (de Moura
et al., 2007; De Moura and Bjørner, 2011). The pro-
cess involves encoding the problem as a first-order
formula incorporating operations from various theo-
ries, such as Boolean logic, bit-vectors, arithmetic,
arrays, and recursive datatypes. The SMT solver then
determines the formula’s satisfiability using advanced
algorithms for SAT solving and theory-specific deci-
sion procedures. In our approach, we integrate the
theories of linear arithmetic and Boolean logic to ver-
ify user authentication possibilities. Employing the
Z3 SMT solver, we obtain either a model or an expla-
nation for the formula’s satisfiability.
2.4 Motivation
Verifiable credentials simplify the replication of phys-
ical identity methods. Users can gather various iden-
tity documents from different providers and use their
attributes to access services. This allows users to
choose which identity to present, similar to real life.
However, users can make mistakes and may uninten-
tionally disclose sensitive information. This research
aims to help users maintain control over their iden-
tity attributes, ensuring they can access services while
minimizing the risk of unauthorized exploitation.
Toward the Foundation of Digital Identity Theory
813

3 METHODOLOGICAL
FRAMEWORK
The methodology followed in this research is illus-
trated in Fig. 1. We begin by translating verifi-
able credentials into product family algebra and then
use an equivalent Boolean logic definition to convert
this algebra into a Boolean formula. Our two ques-
tions are formally specified using the logical equiva-
lent of the refinement operator, facilitating easy res-
olution. Finally, we translate our formulations into a
format compatible with the SMT solver Z3 for auto-
mated resolution. When authentication is successful,
the output is a model of identity attributes required
for authentication. However, to enhance the approach,
we might need to determine the necessary identity at-
tributes if the solver returns ”UNSAT”.
4 TRANFORMING VC TO PFA
EXPRESSION
One of the first steps is to translate the Verifiable Cre-
dentials (VC) or Verifiable Presentation (VP) into a
product family algebra expression. To do this, we use
the W3C specification (Manu et al., 2024) and repre-
sent the VC or VP as a Feature Tree.
Based on the transformation proposed in (H
¨
ofner
et al., 2011), we can easily transform our Feature Tree
into the corresponding Product Family Algebra ex-
pression.
5 PRELIMINARIES
Let us consider F a set of features and P =
d f
P (F) a
set of all possible product (knowing that a product is a
set of features). A collection P (P) is called a product
family.
Definition 1. [J K
F
] J K
F
is the transformation func-
tion of a product family into its Boolean equivalent in
the Disjunctive Normal Form (DNF). More formally
J K
F
is defined as follow:
J K
F
: P (P) −→ (B, ∧, ∨)
JT K
F
=







False if T =
/
0 = 0
V
f ∈F
¬ f if T = {
/
0} = 1
W
t∈T
(
V
f ∈t
f
V
f
′
∈F\t
¬ f
′
) else
Logically, we might be inclined to consider that
for a service provider (verifier), requesting attribute
a from a set of attributes {a, b} does not mean that
he doesn’t want attribute b. This consideration would
lead us to slightly modify the proposed transforma-
tion. However, in the case of identity management,
we rely on the ”Need To Know” principle to consider
that requesting attribute a does not authorize provid-
ing a and b.
subsequently, we introduce Definition 2 and Def-
inition 3 for the reconstruction of the product family
knowing the Boolean formula.
Definition 2. [A (ϕ), A
+
(ϕ), A
−
(ϕ)] Let ϕ be a
boolean formula in DNF form. A(ϕ), A
+
(ϕ) and
A
−
(ϕ) denote respectively the set of all atoms, pos-
itive atoms and negative atoms in ϕ. More formally
A(), A
+
() and A
−
() are defined as follows:
A
+
A
+
(a) = {a}
A
+
(¬a) = { }
A
+
(ϕ
1
∨ ϕ
2
) = A
+
(ϕ
1
) ∪ A
+
(ϕ
2
)
A
+
(ϕ
1
∧ ϕ
2
) = A
+
(ϕ
1
) ∪ A
+
(ϕ
2
)
A
−
A
−
(a) = {}
A
−
(¬a) = { a}
A
−
(ϕ
1
∨ ϕ
2
) = A
−
(ϕ
1
) ∪ A
−
(ϕ
2
)
A
−
(ϕ
1
∧ ϕ
2
) = A
−
(ϕ
1
) ∪ A
−
(ϕ
2
)
A(ϕ) = A
+
(ϕ) ∪ A
−
(ϕ)
Where a is an atomic formula, ϕ
1
and ϕ
2
are
boolean formula in DNF form.
Definition 3. [J K
−1
F
] J K
−1
F
is the inverse function of
J K
F
, which transforms a Boolean formula expressed
in Disjunctive Normal Form (DNF) into an equivalent
product family. More formally:
J K
−1
F
: (B, ∧, ∨) −→ P (P)
J
W
ϕ
i
K
−1
F
=
S
ϕ
i
Jϕ
i
K
−1
F
Jϕ
i
K
−1
F
=



/
0 if A
+
(ϕ
i
)∩
A
−
(ϕ
i
) ̸=
/
0
A
+
(ϕ
i
) × 2
F\A(ϕ
i
)
else
With ϕ
i
a conjunction of atomic Boolean vari-
ables.
The product family algebra operator of interest
is the refinement operator (Definition 6). Checking
whether a user can authenticate himself boils down
to determining whether a product available to the
user refines the product family claimed by the service
provider. In the definitions that follow, we propose
transformations that allow us to express this formula-
tion with logical formulas. Since the refinement re-
SECRYPT 2024 - 21st International Conference on Security and Cryptography
814

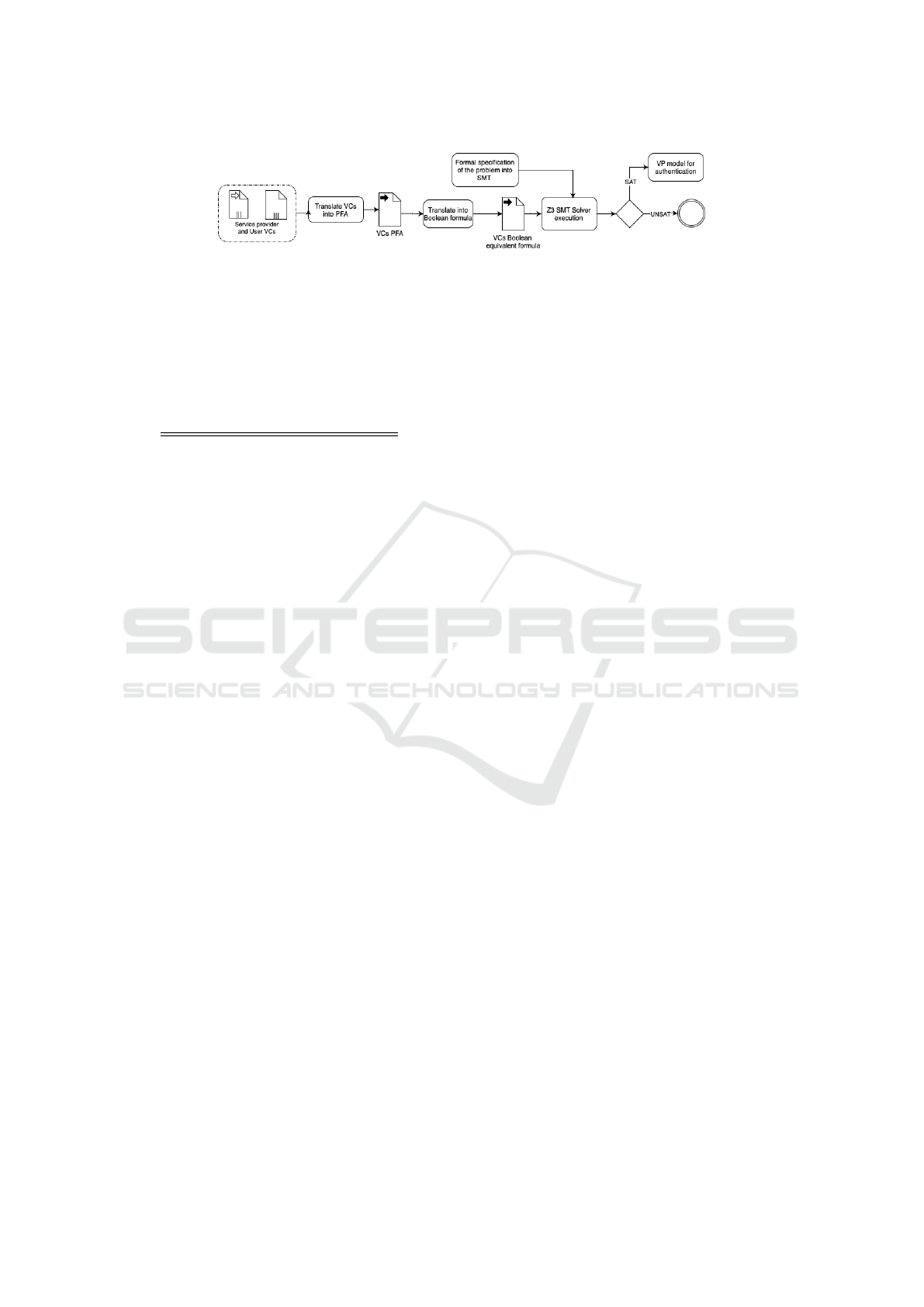
Figure 1: Methodological framework.
lation is a partial order, we take this into account by
integrating the Definition 5.
Definition 4. [⟨ ⟩
+
] Let P be a Boolean formula in
DNF form. ⟨P⟩
+
is the transformation of P into an-
other Boolean formula containing only its positive
atoms. More formally ⟨ ⟩
+
is defined as follows:
⟨ ⟩
+
: (B, ∧, ∨) −→ (B, ∧, ∨)
⟨a⟩
+
= a
⟨¬a⟩
+
= True
⟨P ∧ Q⟩
+
= ⟨P⟩
+
∧ ⟨Q⟩
+
⟨P ∨ Q⟩
+
= ⟨P⟩
+
∨ ⟨Q⟩
+
Where a is an atomic formula, P and Q are
Boolean formulas.
Definition 5. [≼] Let ϕ
1
and ϕ
2
be two Boolean for-
mulas. We define a partial order relation ≼ between
ϕ
1
and ϕ
2
as following: ϕ
1
≼ ϕ
2
if ⟨ϕ
1
⟩
+
=⇒ ⟨ϕ
2
⟩
+
; Where =⇒ is the Boolean implication.
Definition 6. [⊑] Let P and Q be two product family
in P (P). We define the refinement between P and Q,
denoted by P ⊑ Q, as following: P ⊑ Q if JPK
F
≼
JQK
F
.
The refinement operator as defined by PFA (P ⊑
Q) requires that each product in the product family (P)
contains all features of some product in the product
family (Q). In the context of authentication verifica-
tion, this definition is not satisfactory, as the product
family corresponding to the user’s identity could con-
tain a single identity that contains the set of attributes
of some products in the product family claimed by
the service provider. To solve this problem, we intro-
duce, in Definition 7, the notion of partial refinement
(P ⊑
℘
Q); understood here to mean that some prod-
ucts of P contain all the features of some products of
Q.
Definition 7. [⊑
℘
] Let P and Q be two product family
in P (P). We define the partial refinement between P
and Q, denoted by P ⊑
℘
Q, as following: P ⊑
℘
Q if
there exist a product R in P (F) such that R ≤ P and
R ⊑ Q.
Finally, we define (Definition 8) an extension of
the refinement operation which consists, where possi-
ble, in finding a substitution of the values of different
features such that the refinement is true. This def-
inition is motivated by the fact that, in general, the
service provider doesn’t know the values of the at-
tributes, but simply the attributes.
Definition 8. [⊑
Γ
] Let P, Q be two product family in
P (P) and Γ be a set of substitutions. We define the
refinement modulo a substitution in Γ between P and
Q, denoted by P ⊑
Γ
Q, as following: P ⊑
Γ
Q if there
exists a substitution σ in Γ such that σ(P) ⊑ σ(Q).
6 AUTHENTICATION
VERIFICATION
We consider two scenarios: a simple case where the
service provider simply requests identity attributes
and a more realistic case where the service provider
requests a product family with attributes as variables.
6.1 Case Without Variables
6.1.1 Problem Description
The question is : Given a user with a set of verifi-
able credentials and a service provider request, can
the user authenticate to the service provider?
6.1.2 Specification with PFA
Given the user’s product family VC and the prod-
uct family R claimed by the service provider, check-
ing whether the user can authenticate is the same as
checking whether VC partially refines R i.e. VC ⊑
℘
R.
6.1.3 Specification with SMT
Based on our above definitions, checking whether
a user can authenticate is equivalent to checking if
⟨JVCK
F
⟩
+
=⇒ ⟨JRK
F
⟩
+
is satisfiable.
Example 1. Let F = {a, b, c, d, e, f , g, h};
VC = a · b · c + d · e · f
R = a · b + e · f + g · h
Reasoning with PFA
Question : VC ⊑
℘
R ?
Based on the PFA definition of ⊑
℘
, the answer is True
since there exists U = d + c; U ∈ P (2
F
) such that
Toward the Foundation of Digital Identity Theory
815

VC ≤ R ·U.
Reasoning with SMT
Translation into boolean formula:
⟨JVCK
F
⟩
+
= (a ∧ b ∧ c) ∨ (d ∧ e ∧ f )
⟨JRK
F
⟩
+
= (a ∧ b) ∨ (e ∧ f ) ∨ (g ∧ h)
Equivalent question in SMT : Is ⟨JVCK
F
⟩
+
=⇒
⟨JRK
F
⟩
+
satisfiable ?
Verification with Z3 shows that the Boolean formula
is satisfiable and the user can authenticate.
6.2 Case with Variables
6.2.1 Problem
The question here is: Given a user with verifiable cre-
dentials and a provider’s request, what values must
the user assign to the identity attributes to authenti-
cate successfully?.
6.2.2 Specification with PFA
Given the user’s product family VC and the product
family R claimed by the service provider, find the sub-
stitution σ such that σ(VC) ⊑ σ(R).
6.2.3 Specification with SMT
Given a VC =
W
t∈T
(
V
a
i
∈t
a
i
= v
i
) and R =
W
t∈T
′
(
V
a
i
∈t
a
i
=
x
i
) where T and T
′
are, respectively, boolean for-
mula terms representing VC and R, find the model M
of v
i
values to assign to x
i
such that ⟨JVCK
F
⟩
+
=⇒
⟨JRK
F
⟩
+
is satisfiable.
Example 2. Let VC = (a
1
= v
1
) · (a
2
= v
2
) · (a
3
=
v
3
) · (a
4
= v
4
) + (a
4
= v
4
) · (a
5
= v
5
) · (a
6
= v
6
),
R = (a
2
= x
1
)·(a
3
= x
2
)+ (a
4
= x
3
)·(a
6
= x
4
)+ (a
7
=
x
5
) · (a
8
= x
6
),
F = {(a
1
, v
1
), (a
2
, v
2
), (a
3
, v
3
), (a
4
, v
4
), (a
5
, v
5
), (a
6
, v
6
),
(a
2
, x
1
), (a
3
, x
2
), (a
4
, x
3
), (a
6
, x
4
), (a
7
, x
5
), (a
8
, x
6
)}.
Reasoning with PFA
Question : Find σ such that σ(VC) ⊑ σ(R) ?
With σ = {x
1
7→ v
2
, x
2
7→ v
3
, x
3
7→ v
4
}, we have
σ(VC) ⊑ σ(R). However, it’s not easy to find this
sigma when reasoning with the product family.
Reasoning with SMT
Translation into Boolean formula:
⟨JVCK
F
⟩
+
= (a
1
= v
1
) ∧ (a
2
= v
2
) ∧ (a
3
= v
3
)
∧(a
4
= v
4
) ∧ (a
4
= v
4
) ∧ (a
5
= v
5
)
∧(a
6
= v
6
)
⟨JRK
F
⟩
+
= (a
1
= v
1
) ∧ (a
2
= v
2
) ∧ (a
3
= v
3
)
∧(a
4
= v
4
) ∧ (a
4
= v
4
) ∧ (a
5
= v
5
)
∧(a
6
= v
6
)
Equivalent question in SMT : Find a model M such
that ⟨JVCK
F
⟩
+
=⇒ ⟨JRK
F
⟩
+
is satisfiable.
The verification with Z3 shows that the formula is sat-
isfiable with the model M = {x
1
= v
2
, x
2
= v
3
, x
3
=
v
4
, x
4
= v
6
, x
5
=
′′
, x
6
= B} and with that, the user
can authenticate.
7 AUTHENTICATION
VERIFICATION WITH RISK
7.1 Problem
The question is : Given a set of user-verifiable creden-
tials, each of which has claimed properties whose dis-
closure incurs a defined risk, can we identify the veri-
fiable presentation that minimises the user’s risk upon
disclosure ? To address this concern, we introduce the
Definition 9, which allows us to specify the compari-
son between two product families to which risk scores
have been assigned to the attributes.
Definition 9. [≼
r
] Let P, Q be two product family
in P (P). We define an order relation modulo a risk
between P and Q, denoted by P ≼
r
Q, as following:
P ≼
r
Q if r(P) ≤ r(Q).
Where r(P) is a given function that computes the
risk of the product family P. For the sake of simplicity,
we consider the risk of a product family as the total
sum of the risks associated with each of its different
attributes.
Example 3. Let P = a + a · b and r(a) = 5, r(b) = 3:
r(P) = r(a) + r(b) = 8
7.2 Case Without Variables
7.2.1 Specification with PFA
Given 2 product family VC and R whose attributes have
been assigned risk scores, finding the product that en-
ables the user to access the requested service and rep-
resents the minimum risk is the same as finding P such
that the following three conditions are satisfied :
• P ⊑ VC
• P ⊑ R
• ∀P
′
, P
′
⊑ VC ∧ P
′
⊑ R, P ≼
r
P
′
7.2.2 Specification with MAX Weighted SMT
Given 2 product family VC and R whose attributes have
been assigned risk scores, finding the product that en-
ables the user to access the requested service and repre-
sents the minimum risk is the same as finding a model
that satisfies the following objective and constraints.
Objective
Min
∑
v(a
i
) ∗ r(a
i
)
SECRYPT 2024 - 21st International Conference on Security and Cryptography
816

Where a
i
is a VC attribute; v(a
i
) is set to 1 if the at-
tribute is chosen and 0 otherwise; r(a
i
) represents the
risk (here the weight) of the attribute a
i
.
Constraints
• SAT(VC)
• VC =⇒ R
Example 4. Let consider two product family VC and
R such that:
VC = a · b · d + a · b + b · d
R = a · b + b · c + b · d
r(a) = 5, r(b) = 3, r(c) = 6, r(d) = 2.
Reasoning with PFA
Question : Find a product P such that the following
three conditions are satisfied :
• P ⊑ VC
• P ⊑ R
• ∀P
′
, P
′
⊑ VC ∧ P
′
⊑ R, P ≼
r
P
′
We have :
• P
1
= a · b, r(P
1
) = 8 since a · b ⊑ a · b · d + a · b +
b · d and a · b ⊑ a · b + b · c + b · d
• P
2
= b · d, r(P
2
) = 5 since b · d ⊑ a · b · d + a · b +
b · d and b · d ⊑ a · b + b · c + b · d
• P
3
= a · b · d, r(P
3
) = 10 since a · b · d ⊑ a · b · d +
a · b + b · d and a · b · d ⊑ a · b + b · c + b · d
Therefore, product P is P = b · d with risk r(P) = 5.
Reasoning with SMT
By programming the specification with Z3 SMT as
shown in Fig. 2, we determine that the identity at-
tributes to be provided for authentication are b and d.
Thus, the verifiable presentation to be provided to the
service provider is P = b.d with risk r(P) = 5.
Figure 2: Z3 SMT without variables.
7.3 Case with Variables
7.3.1 Specification with PFA
Given 2 product family VC and R whose attributes have
been assigned risk scores, finding the product that en-
ables the user to access the requested service and repre-
sents the minimum risk is the same as finding a substi-
tution σ and a product P such that the following three
conditions are satisfied :
• σ(P) ⊑ σ(VC)
• σ(P) ⊑ σ(R)
• ∀P
′
, σ(P
′
) ⊑ σ(VC)∧ σ(P
′
) ⊑ σ(R), σ(P) ≼
r
σ(P
′
)
7.3.2 Specification with MAX Weighted SMT
Given 2 product family VC and R whose attributes
have been assigned risk scores, finding the product that
enables the user to access the requested service and
represents the minimum risk is the same as finding a
substitution σ and a model that satisfies the following
objective and constraints.
Objective
Min
∑
(a
i
= v
i
) ∗ r(a
i
= v
i
)
Where r(a
i
= v
i
) represent the risk (here the weight) of
attribute a
i
with value v
i
.
Constraints
• SAT(σ(VC))
• σ(VC) =⇒ σ(R)
Example 5. Let consider two product family VC and
R such that:
VC = (a
1
= v
1
) · (a
2
= v
2
) · (a
4
= v
4
)
+(a
1
= v
1
) · (a
2
= v
2
) + (a
2
= v
2
) · (a
4
= v
4
)
Q = (a
1
= x
1
) · (a
2
= x
2
) + (a
2
= x
2
) · (a
3
= x
3
)+
(a
2
= x
2
) · (a
4
= x
4
)
r(a
1
= v
1
) = 5, r(a
2
= v
2
) = 3, r(a
3
= v
3
) =
6, r(a
4
= v
4
) = 2.
Reasoning with PFA
Question : Find a substitution σ based on which we
can obtain a product P such that the following three
conditions are satisfied:
• σ(P) ⊑ σ(VC)
• σ(P) ⊑ σ(R)
• ∀P
′
, σ(P
′
) ⊑ σ(VC) ∧ σ(P
′
) ⊑ σ(R), σ(P) ≼
r
σ(P
′
).
We have :
• σ
1
= {x
1
7→ v
1
, x
2
7→ v
2
, x
3
7→ ””, x
4
7→ ””}, P
1
=
(a
1
= v
1
) · (a
2
= v
2
), r(P
1
) = 8 since (a
1
= v
1
) ·
(a
2
= v
2
) ⊑ (a
1
= v
1
) · (a
2
= v
2
) · (a
4
= v
4
) +
Toward the Foundation of Digital Identity Theory
817

(a
1
= v
1
) · (a
2
= v
2
) + (a
2
= v
2
) · (a
4
= v
4
) and
(a
1
= v
1
) · (a
2
= v
2
) ⊑ (a
1
= v
1
) · (a
2
= v
2
) +
(a
2
= v
2
) + (a
2
= v
2
)
• σ
2
= {x
1
7→ ””, x
2
7→ v
2
, x
3
7→ ””, x
4
7→ v
4
}, P
2
=
(a
2
= v
2
) · (a
4
= v
4
), r(P
2
) = 5 since (a
2
= v
2
) ·
(a
4
= v
4
) ⊑ (a
1
= v
1
) · (a
2
= v
2
) · (a
4
= v
4
) +
(a
1
= v
1
) · (a
2
= v
2
) + (a
2
= v
2
) · (a
4
= v
4
) and
(a
2
= v
2
) · (a
4
= v
4
) ⊑ (a
2
= v
2
) + (a
2
= v
2
) +
(a
2
= v
2
) · (a
4
= v
4
)
• σ
3
= {x
1
7→ v
1
, x
2
7→ v
2
, x
3
7→ ””, x
4
7→ v
4
}, P
3
=
(a
1
= v
1
) · (a
2
= v
2
) · (a
4
= v
4
), r(P
4
) = 10 since
(a
1
= v
1
)· (a
2
= v
2
)· (a
4
= v
4
) ⊑ (a
1
= v
1
)· (a
2
=
v
2
) · (a
4
= v
4
) + (a
1
= v
1
) · (a
2
= v
2
) + (a
2
= v
2
) ·
(a
4
= v
4
) and (a
1
= v
1
) · (a
2
= v
2
) · (a
4
= v
4
) ⊑
(a
1
= v
1
)·(a
2
= v
2
)+(a
2
= v
2
)+(a
2
= v
2
)·(a
4
=
v
4
).
Therefore, σ = {x
1
7→ ””, x
2
7→ v
2
, x
3
7→ ””, x
4
7→ v
4
, }
and the product P is P = (a
2
= v
2
) · (a
4
= v
4
) With
risk of r(P) = 5.
Reasoning with SMT
By programming the specification with Z3 SMT as
shown in Fig. 3, we determine that the model with
the minimum risk is the one with σ = {x
1
7→ ””, x
2
7→
v
2
, x
3
7→ ””, x
4
7→ v
4
}. Therefore, the verifiable pre-
sentation to be provided to the service provider is
P = (a
2
= v
2
) · (a
4
= v
4
) With risk r(P) = 5.
8 RELATED WORK
Despite the proliferation of decentralized identity sys-
tems, there is a dearth of research on privacy preser-
vation in user-centric identity management through
formal approaches that consider risks directly associ-
ated with identity attributes. Some studies have ad-
dressed user-centric privacy by focusing on context-
related risks.
Jafari et al. (Jafari-Lafti et al., 2009) introduced
P2F, a recommendation tool that analyzes a user’s
transaction history and privacy preferences, along with
real-world privacy guidelines, to prevent unintended
disclosure of personal information. This tool uses
a risk assessment model based on service providers’
properties, potential collusion between providers, sen-
sitivity of disclosed information, and the risk of link-
ing to undesirable transactions. Similarly, (Ahn and
Sekar, 2011) proposed a risk-based approach to help
users evaluate the risk level of disclosing their iden-
tity in user-centric identity management, employing
ontology-based evaluation and privacy preference as-
sessment. However, these approaches focus on contex-
tual elements without directly considering the value of
identity attributes.
Zaeem et al. (Chang et al., 2018) proposed two
methods, using the Identity Threat Assessment and
Prediction (ITAP) database, to aid in evaluating and
identifying the optimal set of Personally Identifiable
Information (PII) that meets authentication goals while
minimizing risk exposure. The static approach assigns
risk and uniqueness scores to identity attributes, com-
bining these to determine a final score. The dynamic
approach uses Bayesian networks to infer the risk score
of an attribute, considering its accessibility and the po-
tential impact of inappropriate disclosure. Zaeem et al.
(Zaeem et al., 2016) work provides a useful foundation
for assigning risk scores to identity attributes.
9 DISCUSSION
A notable contribution of this paper is the translation of
product family algebra into Boolean logic, enabling the
automatic verification of constraints associated with
product families using SAT or SMT solvers. This ad-
vancement facilitates the rapid and reliable detection of
errors or conflicts in product configurations.
In the authentication protocol, the service
provider’s request sets the context and defines specific
constraints for user authentication. By interpreting
verifiable credentials and the service provider’s request
as product families and translating them into Boolean
formulas, we simplify the verification process. Our
research demonstrates that determining a user’s ability
to authenticate becomes straightforward when framed
as a satisfiability problem.
Our findings also indicate that integrating an SMT
solver into a user’s digital wallet could lead to a new
generation of intelligent wallets. These wallets would
not only secure assets but also assist users in mak-
ing informed decisions, personalizing their experience,
and navigating the decentralized identity ecosystem.
They could transparently disclose identity attributes
with minimal harm, provided the attributes are cor-
rectly encoded and risks properly characterized.
Verifiable credentials are inherently more complex
than our current research scope, involving metadata,
claims, and proof. Even if a user possesses all the at-
tributes required by a service provider, authentication
may fail if the service provider cannot verify the iden-
tity’s origin.
10 CONCLUSION
The increasing use of verifiable credentials brings us
closer to the conventional practice of physical iden-
tity, allowing users to select among multiple identities
for service access, provided the service provider ac-
cepts the chosen identity. Our research demonstrates
SECRYPT 2024 - 21st International Conference on Security and Cryptography
818

Figure 3: Z3 specification with variables and result (on the right).
that formal methods can enhance information security
by leveraging product family algebra and Satisfiability
Modulo Theories (SMT) to verify user access. Addi-
tionally, we address the risk associated with disclosing
specific identity attributes, thereby enhancing privacy
protection and adhering to the need-to-know principle.
We show that Max weighted SMT automates and re-
solves the disclosure of identity attributes with minimal
risk, facilitated by the Z3 solver.
This approach can be integrated into a decentral-
ized identity management system, which will be the
next step in our research. We also plan to refine this ap-
proach by considering the creation of verifiable presen-
tations from verifiable credentials, including attribute
aggregation where possible.
REFERENCES
Ahn, G.-J. and Sekar, P. (2011). Ontology-based risk eval-
uation in user-centric identity management. In 2011
IEEE International Conference on Communications
(ICC), pages 1–5. IEEE.
Chang, K. C., Zaeem, R. N., and Barber, K. S. (2018). En-
hancing and evaluating identity privacy and authenti-
cation strength by utilizing the identity ecosystem. In
Proceedings of the 2018 Workshop on Privacy in the
Electronic Society, pages 114–120.
De Moura, L. and Bjørner, N. (2011). Satisfiability modulo
theories: introduction and applications. volume 54,
pages 69–77. ACM New York, NY, USA.
de Moura, L., Dutertre, B., and Shankar, N. (2007). A tu-
torial on satisfiability modulo theories: (invited tuto-
rial). In International conference on computer aided
verification, pages 20–36. Springer.
H
¨
ofner, P., Khedri, R., and M
¨
oller, B. (2011). An algebra
of product families. Software & Systems Modeling,
10:161–182.
Jafari-Lafti, M., Huang, C.-T., and Farkas, C. (2009). P2f:
A user-centric privacy protection framework. In 2009
International Conference on Availability, Reliability
and Security, pages 386–391. IEEE.
Li, Y., Fu, Y., Du, Z., and Cai, Z. (2022). An access control
scheme based on decentralized identifiers and verifi-
able credentials in iot. In 2022 3rd International Con-
ference on Computer Science and Management Tech-
nology (ICCSMT), pages 279–283. IEEE.
Lim, S., Rhie, M.-H., Hwang, D., and Kim, K.-H.
(2021). A subject-centric credential management
method based on the verifiable credentials. In 2021
International Conference on Information Networking
(ICOIN), pages 508–510. IEEE.
Manu, S., Dave, L., David, C., and Orie, S. (2024). Veri-
fiable credentials data model v2.0. Draft Community
Group Report.
Manu, S., Dave, L., Markus, S., Drummond, R., Orie, S.,
and Christopher, A. (2022). Decentralized identifiers
(dids) v1.0 : Core architecture, data model, and repre-
sentations.
Xu, L., Li, T., and Erkin, Z. (2023). Verifiable creden-
tials with privacy-preserving tamper-evident revoca-
tion mechanism. In 2023 Fifth International Con-
ference on Blockchain Computing and Applications
(BCCA), pages 266–273. IEEE.
Zaeem, R. N., Budalakoti, S., Barber, K. S., Rasheed, M.,
and Bajaj, C. (2016). Predicting and explaining iden-
tity risk, exposure and cost using the ecosystem of
identity attributes. In 2016 IEEE International Car-
nahan Conference on Security Technology (ICCST),
pages 1–8. IEEE.
Toward the Foundation of Digital Identity Theory
819