Bernoulli Distribution-Based Maximum Likelihood Estimation for

Dynamic Coefficient Optimization in Model-Contrastive Federated

Learning

Sichong Liao

Department of Electronic and Electrical Engineering, University of Sheffield, Sheffield, S10 2TN, U.K.

Keywords: Bernoulli Distribution, Maximum Likelihood Estimation, Loss Term, Federated Learning

Abstract: In the realm of federated learning, the non-identically and independently distributed (non-IID) nature of data

presents a formidable challenge, often leading to suboptimal model performance. This study introduces a

novel Bernoulli Distribution-Based Maximum Likelihood Estimation for Dynamic Coefficient Optimization

method in Model-Contrastive Federated Learning, aiming to address these inherent difficulties. The center of

the proposed approach is the dynamic adjustment of loss terms concurring to quantifying deviation between

the global model and local model. There may be a lot of variation in the data. In this case, the proposed manner

could upgrade the robustness and adaptability of the model itself. Leveraging a Model-Contrastive Federated

Learning (MOON) framework, this paper proposed a Dynamic Coefficient Optimized MOON (DCO-MOON)

framework. For the supervised loss term and model-contrastive loss term, the proposed approach incorporates

a dynamic coefficient adjustment mechanism. The efficacy of this approach is illustrated through the

simulations on different datasets, including the Modified National Institute of Standards and Technology

(MNIST), Fashion-MNIST, and Canadian Institute for Advanced Research (CIFAR-10). Experimental results

show improvements in test accuracy and communication efficiency. It also illustrates that DCO-MOON can

superiorly adjust to real-world scenarios, which are confronting data-driven challenges with non-IID and

unbalanced datasets.

1 INTRODUCTION

In recent years, data privacy and security have

become fundamental concerns within the field of

machine learning (Voigt & Bussche, 2017, Kingston,

2017). Conventional centralized training strategies

regularly require the aggregation of large datasets,

posing huge risks in terms of data privacy and

security flaws. Moreover, these strategies can be

inefficient due to the demanding job of transferring

vast amounts of data to a central server. Federated

learning's strategy of training models over different

devices by keeping data local is designed to address

these issues (Li et al, 2021).

Federated Learning speaks to a distributed

machine-learning system. It can benefit a lot from

prioritizing privacy (Li et al, 2020, Yang et al, 2019).

In this case, clients, also known as parties, work

collaboratively in the training of a centralized model.

This collaboration is then encouraged through the

sharing of model-related data. Such parameters or

updates will be exchanged instead of transmitting

their private datasets. Each client uses its local data to

train a local model. Then the central server aggregates

the model parameters of local models to train a global

model. These aggregated model parameters are later

communicated along these lines to the clients. Due to

its privacy and efficiency performance in distributed

settings, federated learning is regarded as a great

advancement in distributed machine learning (Tyagi

et al, 2023). It allows two or more parties to

collaboratively train models without sharing raw data.

This system is vital in today's data-driven world

where data privacy and security are fundamental.

Be that as it may, one of the primary challenges in

federated learning is the non-identically distributed

(non-IID) nature of data over different clients

(Kairouz et al, 2021, Zhu et al, 2021). Due to different

user behaviors and preferences, the data generated by

distinctive parties often varies widely. In this case,

this leads to non-IID distributions. The so-called non-

504

Liao, S.

Bernoulli Distribution-Based Maximum Likelihood Estimation for Dynamic Coefﬁcient Optimization in Model-Contrastive Federated Learning.

DOI: 10.5220/0012827600004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 504-511

ISBN: 978-989-758-690-3

IID issue regularly leads to model performance

decline due to the varying data distributions among

participating clients (Li et al, 2020, Li et al, 2019).

The statistical heterogeneity is also known as a direct

result of the non-IID issue. And that is what got

federated models into trouble with uneven

performance and convergence issues.

As a pivotal method in federated learning,

FedAvg aims to address the challenges of

communication efficiency and data privacy

(McMahan et al, 2017). It works by averaging local

stochastic gradient descent (SGD) updates for the

primal problem. Over numerous experiments, it has

been found effective for non-convex problems (Su et

al, 2023). FedAvg combines models by averaging

local model parameters from all clients. In any case,

it is noted that FedAvg can struggle with convergence

in settings with heterogeneous data. Dealing with data

heterogeneity frequently leads to suboptimal

convergence or even divergence of the global model.

Tending to this issue, recent research has focused on

Bayesian non-parametric methods for aggregation of

two or more models. That includes neuron matching

and merging local models, as seen in approaches like

PFNM and Claici et al. (Yurochkin et al, 2019, Claici

et al, 2020). Besides, Shukla et al. presented the

Infogain FedMA algorithm. This algorithm utilizes a

strategy based on information-gain sampling for the

selection of model parameters and joins probabilistic

federated neural matching (Shukla & Srivastava,

2021). Though these approaches appear workable and

innovative, they may not have mainly been used with

more complex neural networks. Applying them to

more complex networks to broaden their use is a

developing research area.

Li, He, and Song's Model-Contrastive Federated

Learning (MOON) strategy may be an outstanding

progression in dealing with non-IID data issues (Li et

al, 2021). By combining model-contrastive loss,

similar to NT-Xent loss for contrastive representation

learning, it optimizes the learning process over

distributed networks. And this improves federated

learning's effectiveness. Such tasks like image

classification can benefit a lot from the MOON

technique.

In this work, this paper will deal with non-IID

issues by utilizing a Bernoulli Distribution-Based

Maximum Likelihood Estimation for Dynamic

Coefficient Optimization (DCO). It is a more

comprehensive framework based on MOON. This

new framework merges statistical techniques with

federated learning. Based on local and global model

differences, it could reasonably adjust the supervised

loss term and model-contrastive loss term, and thus

improve accuracy and communication efficiency.

This article also illustrates that DCO-MOON can

superiorly adjust to real-world scenarios, which are

confronting data-driven challenges with non-IID and

unbalanced datasets.

2 METHODOLOGY

To integrate the dynamic coefficient optimization

within the model-contrastive federated learning

framework, there is no gainsaying the fact that

integration is premised on a principal perception: in

non-IID data settings, local models in a federated

learning system show varying degrees of deviation

from the global model. Based on the condition, the

deviation between the global model and the local

model can be evaluated by a quantification method.

For example, given deviations generated by model

training and aggregation between the global model

and the local model, it is not wise to aggregate the

features learned by the bad local models into the

global model in an unbalanced way. The model

updates instructed by gradient descent should not

uncontrollably aggravate the polarization between the

global model and local models. That is to say, these

deviations could be detected through a statistical

method. And then take proactive adjustments to

optimize gradient descent to a certain degree.

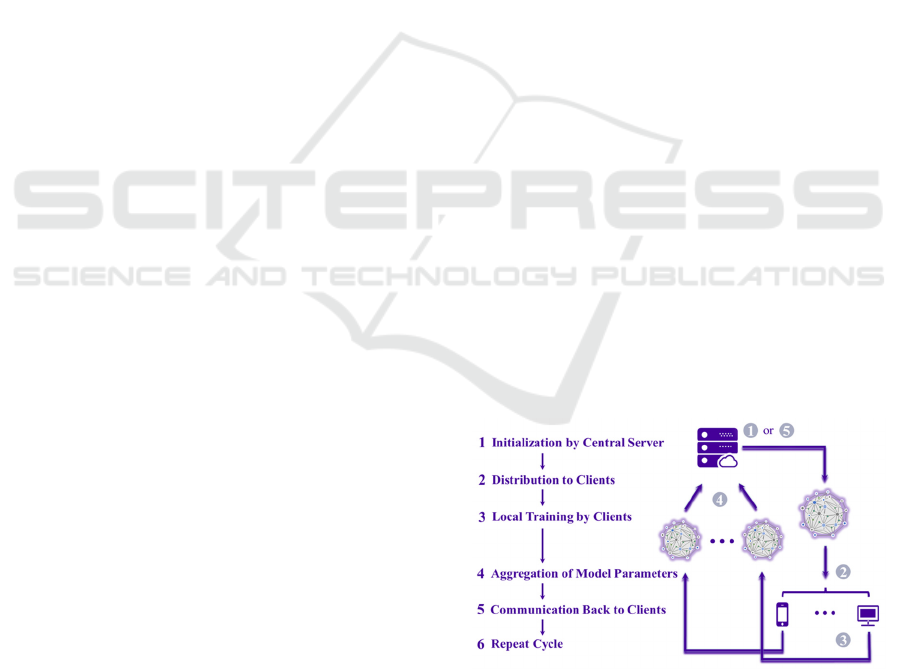
The common cycle of federated learning is shown

in Figure 1. The proposed system follows the cycle of

its initialization, build-up, and repeat stages.

Figure 1: The cycle of common federated learning

(Photo/Picture credit: Original).

Bernoulli Distribution-Based Maximum Likelihood Estimation for Dynamic Coefﬁcient Optimization in Model-Contrastive Federated

Learning

505

2.1 Quantifying Deviation with

Bernoulli Distribution-Based MLE

To address non-IID issues, this paper presents a novel

mechanism for quantifying and reacting to these

deviations. Since there is always drift in the phase of

local training, this approach first characterizes a

metric for critical deviation. For each local model

i

at round

t , this work calculates the Euclidean

distance

t

i

d between its parameter vector

t

i

w and the

parameter vector

t

g

lobal

w

of global model. In the

following, mitigating the impact of scale differences

is needed. The Euclidean distance is then normalized

according to the norm of the global model's

parameters. So far, the Euclidean distance

t

i

d is

calculated to quantify the deviation:

()

2

(, )

1

Δ

K

tt

iik

k

dw

=



(1)

Where

1

Δ

ttt

ii

www

−

=− can denote the distinction

in parameters between the current model state and

previous one. And

K

is the total number of

parameters. Here, normalization is to ensure

comparability:

-1

Normalized

t

i

t

d

w

=

(2)

A binary outcome function

t

i

b is then defined to

indicate significant deviation. The threshold

θ

serves as a hyper-parameter. This allows it to be

customized by a certain real-world situation:

1, if

0, otherwise

t

i

d θ

b



>



=



(3)

The normalized deviation is utilized to inform a

binary outcome function

t

i

b , adhering to a Bernoulli

distribution. This function essentially categorizes

each local model's update as significantly deviating or

not, based on a pre-set threshold

θ

.

Maximum Likelihood Estimation (MLE) is a

statistical method used to estimate the parameters of

a statistical model. It selects the parameter values that

maximize the likelihood function, representing the

most probable values given the observed data. In the

context of federated learning, MLE can be utilized to

estimate the probability of deviation in local models

from a global model. Given that each local model in

the federated learning framework is independently

trained, the samples in the dataset are assumed to be

independently and identically distributed. This article

utilizes the Bernoulli distribution to derive the MLE

of the parameter

t

p

. The observed sample set is

denoted as

12

{ , , ... , }

tt t

N

Bbb b

= , where each

t

i

b

represents a binary outcome indicating significant

deviation of the i-th local model at round

t . The

likelihood function, which is the probability of

observing the sample set

B

given the parameter

p

,

is expressed as:

()()

()

1

t

i

N

b

i

LpB f Bp p p

−

=

== −

∏

(4)

The log-likelihood function also known as the

logarithm of the likelihood function. It is defined as:

()

1

log log 1 log 1

N

tt

ii

i

LpB b p b p

=





=+−−







(5)

To get the MLE of

t

p

, the value of

p

that

maximizes the log-likelihood function is determined.

It first takes the derivative of the log-likelihood

function with respect to

p

. Then ensuring that this

derivative equals zero is needed:

()

1

log 0

1

t

N

i

b

LpB

ppp

=



−

∂



=−=

∂−







(6)

A MLE of the Bernoulli parameter is then yielded

after solving Formula 6 for

p

:

1

N

t

ti

i

p

b

N

=



(7)

In this way, the MLE of the probability

t

p

of

deviation is calculated over all local models. In the

local models at each round

t , the empirical

probability of observing a significant deviation is

defined. Under the settings of non-IID and

unbalanced dataset, it is a reasonably statistical metric

and therefore could have a clear understanding of the

dynamics and behavior of local models. In the

following work, this paper will introduce how

dynamic coefficient optimization is implemented and

then proposed a DCO-MOON framework. That is to

say, the learning process could be continuously fine-

tuned in reaction to the deviation.

ICDSE 2024 - International Conference on Data Science and Engineering

506

2.2 Proposed Dynamic Coefficient

Optimized MOON

To achieve seamless integration between Bernoulli

Distribution MLE and MOON framework, this paper

proposed a Dynamic Coefficient Optimized MOON

(DCO-MOON) framework. The integration is

fastidiously designed to dynamically adjust the

coefficient of two loss terms, respectively. According

to the deviation probability

t

p

of the local models,

proposed framework can superiorly adjust to real-

world scenarios, which are confronting data-driven

challenges with non-IID and unbalanced datasets.

The DCO-MOON starts with the central server

initializing the global model

0

w

, which is the same

as the MOON system. However, the DCO-MOON

framework distinguishes itself through the

introduction of a dynamic adjustment process for the

learning coefficients. Initially, at

0t =

, the base

learning coefficient is set to a predefined value

μ

. As

the training progresses, the framework deviates from

the traditional MOON model by employing the

Bernoulli MLE to calculate the deviation probability

t

p

as follows:

1

N

t

ti

i

p

b

N

−

=



(8)

This probability then informs the adjustment of the

learning coefficients in next round, defined as:

tt

p

μμ

⋅

=

(9)

In the local training phase, each client model

computes the difference vector

1

Δ

ttt

ii

www

−

=− and

the normalized Euclidean distance

t

i

d as Formula 2. A

binary outcome

t

i

b , indicating a significant model

deviation, is determined based on the threshold

θ

.

A critical innovation in the DCO-MOON

framework is the redefinition of the total loss function

l

to incorporate dynamically adjusted coefficients,

termed as "Dynamic Coefficients". These coefficients,

(2 )

t

μ

−

μ

and

()

t

μμ

+

, are applied to the

supervised and model-contrastive components of the

loss function, respectively. The loss function of

MOON and modified loss function of DCO-MOON

is given by:

()

()( )

1

;, ; ;;

tttt

MOON sup i con i i

llwxyμ lwwwx

−

=+⋅

(10)

() ()

() ( )

1

2;,();;;

tttt

DCO MOON t sup i t con i i

l μμ lwxy μμlwwwx

−

=−⋅ ++⋅

(11)

This alteration allows for a flexible adjustment of the

learning process, adapting to the varying degrees of

deviation in the local models.

After a round of local training, the local models

update their parameters using this adaptive loss

function and return the updated model

t

i

w along with

the deviation outcome

t

i

b to the server. The server

then aggregates these models to form the updated

global model

1t

w

+

, employing a weighted scheme

reflective of their contributions.

The overall DCO-MOON framework is shown in

Figure 2. During each round, the central server

dispatches the global model to the clients and

subsequently gathers the updated local models from

them. The global model is then refined through a

process of weighted average computation. In the

phase of local model training, each client applies

SGD to adjust the global model using their unique

dataset. The objective for this adjustment is shown in

Formula 12.

()

() ()

()

1

sup

,~

m2 ;, ;;n;i

t

i

tttt

ti tconii

xy D

w

lwxy lwwwx

−



μ−μ + μ+μ



E

(12)

The Dynamic Coefficient Optimized MOON

framework brings forth an adaptive, responsive

approach to model training and aggregation,

specifically tailored to overcome the complexities

associated with non-IID and unbalanced datasets. By

dynamically modulating learning coefficients based

on real-time model behavior, the DCO-MOON

framework promises improved convergence and

model performance in diverse federated learning

environments.

Bernoulli Distribution-Based Maximum Likelihood Estimation for Dynamic Coefﬁcient Optimization in Model-Contrastive Federated

Learning

507

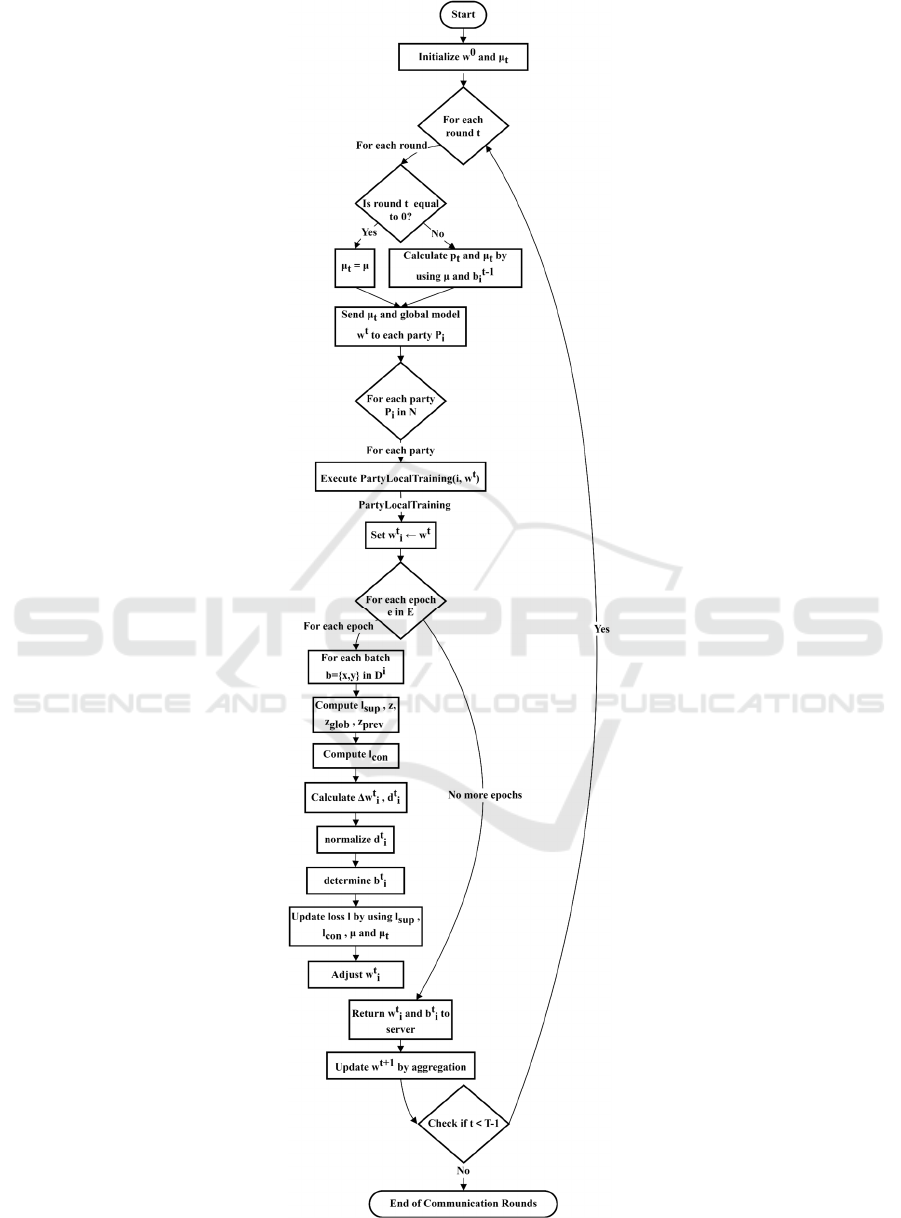
Figure 2: The DCO-MOON framework (Photo/Picture credit: Original).

ICDSE 2024 - International Conference on Data Science and Engineering

508

3 RESULTS & EVALUATION

In this section, proposed approach evaluates the

performance of FL algorithms, including FedAvg,

FedProx, MOON, SOLO and proposed DCO-MOON

(Li et al, 2020, McMahan et al, 2017, Li et al, 2021).

First, this article introduces experimental setup. The

accuracy and communication efficiency of proposed

DCO-MOON framework is then shown in

comparison with other up-to-date federated learning

algorithms. For fair comparison, DCO-MOON and

all baselines are in non-IID settings.

To validate the effectiveness of DCO-MOON,

this research conducted a series of simulations using

a customized federated learning platform. These

simulations were designed to address non-IID and

unbalanced datasets. The simulations were carried out

on PyCharm. It utilized three datasets, which include

MNIST, Fashion-MNIST and CIFAR-10, to ensure a

comprehensive evaluation. CIFAR-10 is generated by

using Dirichlet distribution to create the non-IID data

partition among clients. For the CIFAR-10 dataset,

this paper proposed an approach. It utilizes a CNN

network as the base encoder. Besides, it comprises

two convolutional layers: the first convolutional layer

has 32 filters with a kernel size of 5x5, followed by a

ReLU activation and a 2x2 max pooling layer. The

second convolutional layer consists of 64 filters, also

with a 5x5 kernel, followed by a ReLU activation and

another 2x2 max pooling layer. Following the

convolutional layers, the network includes a fully

connected layer with an input dimensionality of 1600,

flattened from the output of the convolutional layers,

and an output size of 512. A final fully connected

layer maps to the number of classes, which is 10 for

the CIFAR-10 dataset. For the CIFAR-10 dataset, the

projection head in the Convolutional Federated

Learning Model is configured as a single fully

connected layer, originally serving as the final layer

of the model. This configuration is distinct from a

traditional 2-layer MLP, with the output dimension of

the projection head being aligned with the number of

classes as defined in the model's architecture. For fair

comparison, all baselines, including FedAvg and

MOON, adopt this network architecture and utilize

the same structure for the projection head.

The present study rigorously investigates the

influence of the hyperparameter µ on the performance

of DCO-MOON. Experimental adjustments of µ

within the set {0.1, 1, 5, 10} were conducted, and the

optimal results are documented in Table 1. This table

illustrates the test accuracy of DCO-MOON with

varying µ values across datasets such as MNIST,

Fashion-MNIST, and CIFAR-10. Note that the

optimal value of µ for DCO-MOON was consistently

identified as 5 for all three datasets. It is pertinent to

mention that similar hyperparameters exist in MOON

and FedProx, with MOON having a µ value of 1 and

FedProx a µ value of 0.001. Unless specified

otherwise, the experiments proceeding within this

article will adhere to these default settings.

Table 1: Test accuracy of DCO-MOON with

μ

from

{

}

0.1 1 5 10

,, ,

on different datasets.

μ

MNIST Fashion-MNIST

CIFAR-10

0.1 96.9% 81.7% 65.7%

1 97.4% 84.2% 68.3%

5 98.3% 85.4% 69.5%

10 98.0% 84.8% 68.6%

Table 2 presents the top-1 test accuracies of

various federated learning algorithms. Under non-IID

settings, the SOLO algorithm showed obviously

lower accuracy compared to other FL algorithms.

DCO-MOON consistently outperformed other FL

algorithms in all tasks. When assessing the average

accuracy across all datasets, DCO-MOON surpassed

MOON by 1.4%. While MOON's performance was

inferior to DCO-MOON, it was superior to other FL

algorithms. For FedProx, its test accuracy closely

aligned with FedAvg, with slightly higher accuracy

on the Fashion-MNIST and CIFAR-10 datasets.

Given the small µ value, the proximal term in

FedProx (i.e.,

F

edProx FedAvg prox

Ll l=+

μ

⋅

) had a

minimal impact on the training process.

Bernoulli Distribution-Based Maximum Likelihood Estimation for Dynamic Coefﬁcient Optimization in Model-Contrastive Federated

Learning

509

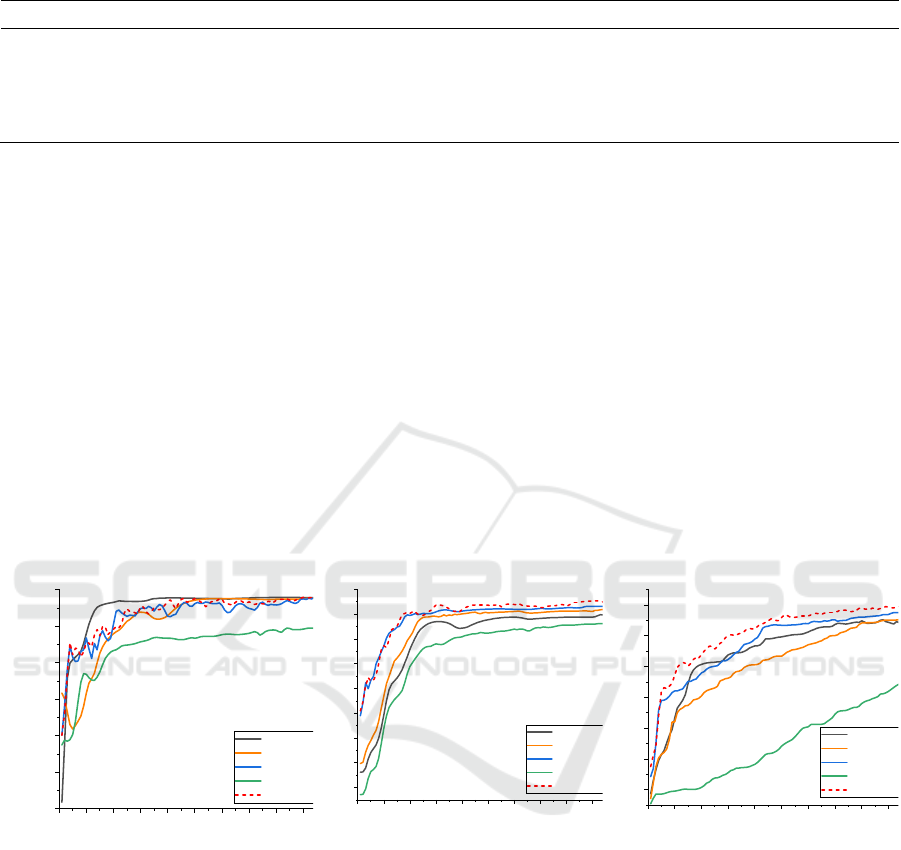
Table 2: Test accuracy of different FL algorithms on different datasets.

FL algorithms MNIST Fashion-MNIST

CIFAR-10

Fe

d

Av

g

97.9% 79.8% 65.2%

FedProx 97.7% 81.9% 65.9%

MOON 98.1% 83.1% 67.8%

SOLO 89.8% 76.4% 45.7%

DCO-MOON 98.3% 85.4% 69.5%

Figure 3 describes the Top-1 accuracy per training

round. Compared to MOON, DCO-MOON's model-

contrastive loss had a more positive effect on the

convergence speed of the optimal algorithm. Initially,

the accuracy improvement rate of DCO-MOON was

almost same as MOON. However, it achieved better

accuracy later due to the more positive impact of the

model-contrastive loss. Consequently, the test

accuracy of MOON and FedAvg gradually diverged

from that of DCO-MOON as the number of

communication rounds increased. For FedProx, the

optimal µ value is typically small. Thus, the

increasement of FedProx closely resembles FedAvg,

especially on Fashion-MNIST. However, with a

setting

1=

μ

, FedProx operates at a considerably

slower pace due to the added proximal term. This

illustrates that a big µ value in FedProx leads to slow

convergence and poor accuracy. So it indicates that

restricting the L2-norm distance between local and

global models is not an effective solution. While

MOON's model-contrastive loss can effectively

enhance accuracy without decelerating convergence,

DCO-MOON amplifies this positive effect. The

dynamic constraint of model-contrastive loss and

supervised loss actively adjusts with deviation,

particularly noticeable when there is a significant

change in deviation between the global and local

models. Furthermore, DCO-MOON required

significantly fewer communication rounds to achieve

similar accuracy levels compared to FedAvg. On

CIFAR-10, DCO-MOON necessitated approximately

half the communication rounds of FedAvg. This

highlights its better performance on communication

efficiency.

0 102030405060708090

40

50

60

70

80

90

100

Top-1 accuracy (%)

Communication rounds

FedAvg

FedProx

MOON

SOLO

DCO-MO

O

0 102030405060708090

10

20

30

40

50

60

70

80

90

Top-1 accuracy (%)

Communication rounds

FedAvg

FedProx

MOON

SOLO

DCO-MO

O

0 102030405060708090

10

20

30

40

50

60

70

Top-1 accuracy (%)

Communication rounds

FedAvg

FedProx

MOON

SOLO

DCO-MO

O

(a) MNIST (b) Fashion-MNIST (c) CIFAR-10

Figure 3. The top-1 accuracy on different datasets with the number of communication rounds T = 100 (Photo/Picture credit:

Original).

4 CONCLUSION

This paper proposed DCO-MOON, which can

achieve a better performance on merging supervised

loss and model-contrastive loss. It designs a dynamic

adjustment mechanism according to quantifying

deviation between global model and local model.

Experimental results also demonstrate that DCO-

MOON achieve a better performance on accuracy and

communication efficiency. DCO-MOON can better

adapt to real-world scenario, which is facing data-

driven challenges with non-IID and unbalanced

datasets. In future works, evaluating the deviation

between global and local models in a more detailed

and quantitative way and designing corresponding

loss term adjustment mechanisms, are also research

directions worth exploring.

ICDSE 2024 - International Conference on Data Science and Engineering

510

REFERENCES

P. Voigt, and A. Von dem Bussche, A Practical Guide, 1st

Ed., Cham: Springer International Publishing

10(3152676), 10–5555, (2017).

J. Kingston, Artificial Intelligence and Law, 25(4), 429–

443 (2017).

Q. Li, Z. Wen, Z. Wu, S. Hu, N. Wang, Y. Li, X. Liu, and

B. He, IEEE Trans. Knowl. Data Eng., (2021).

T. Li, A.K. Sahu, A. Talwalkar, and V. Smith, IEEE Signal

Process. Mag. 37(3), 50–60, (2020).

Q. Yang, Y. Liu, T. Chen, and Y. Tong, ACM Transactions

on Intelligent Systems and Technology (TIST) 10(2),

1–19, (2019).

S. Tyagi, I.S. Rajput, and R. Pandey, “Federated learning:

Applications, Security hazards and Defense measures”.

in 2023 International Conference on Device

Intelligence, Computing and Communication

Technologies, (DICCT) (2023), pp. 477–482.

P. Kairouz, H.B. McMahan, B. Avent, A. Bellet, M. Bennis,

A.N. Bhagoji, K. Bonawitz, Z. Charles, G. Cormode, R.

Cummings, and others, Foundations and Trends® in

Machine Learning, 14(12), 1–210, (2021).

H. Zhu, J. Xu, S. Liu, and Y. Jin, Neurocomputing, 465,

371–390, (2021).

T. Li, A.K. Sahu, M. Zaheer, M. Sanjabi, A. Talwalkar, and

V. Smith, Proceedings of Machine Learning and

System,s 2, 429–450, (2020).

X. Li, K. Huang, W. Yang, S. Wang, and Z. Zhang, arXiv

Preprint arXiv:1907.02189, (2019).

B. McMahan, E. Moore, D. Ramage, S. Hampson, and B.A.

y Arcas, “Federated learning: Applications, Security

hazards and Defense measures”. in Proceedings of the

20th International Conference on Artificial Intelligence

and Statistics, edited by A. Singh and J. Zhu (PMLR,

2017), pp. 1273–1282.

S. Su, B. Li, and X. Xue, Neural Networks, 164, 203–215,

(2023).

M. Yurochkin, M. Agarwal, S. Ghosh, K. Greenewald, N.

Hoang, and Y. Khazaeni, “Bayesian Nonparametric

Federated Learning of Neural Networks”. in

Proceedings of the 36th International Conference on

Machine Learning, edited by K. Chaudhuri and R.

Salakhutdinov, (PMLR, 2019), pp. 7252–7261.

S. Claici, M. Yurochkin, S. Ghosh, and J. Solomon, “Model

Fusion with Kullback-Leibler Divergence”. in

Proceedings of the 37th International Conference on

Machine Learning, edited by H.D. III and A. Singh,

(PMLR, 2020), pp. 2038–2047.

S. Shukla, and N. Srivastava, “Federated matched

averaging with information-gain based parameter

sampling”. in Proceedings of the First International

Conference on AI-ML Systems, (Association for

Computing Machinery, New York, NY, USA, 2021),

pp. 1-7.

Q. Li, B. He, and D. Song, “Model-contrastive federated

learning”. in Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, (2021),

pp. 10713–10722.

Bernoulli Distribution-Based Maximum Likelihood Estimation for Dynamic Coefﬁcient Optimization in Model-Contrastive Federated

Learning

511