A Framework for Federated Analysis of Health Data Using

Multiparty Homomorphic Encryption

Miroslav Puskaric

High Performance Computing Center Stuttgart (HLRS), University of Stuttgart, Nobelstraße 19, 70569 Stuttgart, Germany

Keywords: Federated Data Analysis, Homomorphic Encryption Application, Multi-Party Computing.

Abstract: Although federated data analysis represents a significant contribution toward ensuring data privacy, the risk

of information leakage from the intermediate results exchanged during the analysis process still exists. These

risks become even more emphasised when analysing sensitive data such as health records. One of the

approaches to mitigate these issues is homomorphic encryption, a novel encryption algorithm which allows

for performing computations over encrypted data. This article presents a federated data analysis framework

where intermediate analysis results are exchanged and processed as ciphertexts and where data sources are

connected in a decentralised manner by forming multiple clusters, with each cluster having a central node.

Besides processing encrypted information, another advantage of the homomorphic encryption algorithms is

the support for a multiparty encryption scheme. A workflow for creating a shared public and evaluation key

is presented, where central nodes are part of the workflow and data sources only receive the shared keys.

Furthermore, as data analysis examples, workflows for Kaplan-Meier survival analysis and distributed mean

value are presented, whose results do match those obtained through centralized analysis. As a last step of the

federated data analysis, multiparty decryption of the final result occurs.

1 INTRODUCTION

In health data analysis, where datasets consist of

patients’ health records, numerous security and

privacy requirements need to be met before sharing

data for analysis purposes. Since health data is

considered sensitive and is subject to strict data

protection legislation, a secure and reliable

framework that prevents data leakage and protects

patient information is a prerequisite. In a European

context, All EU member states have been introduced

to the General Data Protection Regulation (GDPR)

act on data protection and privacy, which defines,

among others, the use of health data for patient

treatment and research purposes. Still, these countries

have additional data protection acts for the use of

health data put into force (Hansen et al., 2021), which

can hinder data sharing and make the legal framework

challenging to interpret, especially in the case of

cross-border data sharing. Federated data analysis is

one of the approaches that can address the before-

mentioned challenges. The federated approach allows

data analysis algorithms to be applied to remotely

https://orcid.org/0000-0003-2487-8822

located datasets without sharing data directly with the

data analyst. Instead, intermediate analysis results are

exchanged and combined with results from other data

sources. However, it has been proven that

intermediate results can be exploited to retrieve

information on background data (Zhu et al., 2019;

Yang et al., 2023). One approach towards mitigating

these issues would be to exchange all information in

an encrypted format by encoding data into

ciphertexts. This would prevent access to plaintext

information without the corresponding decryption

key, while still allowing data computation.

The above-mentioned approach can be addressed

by using homomorphic encryption (HE) (Naehrig et

al., 2011), which is an encryption algorithm capable

of performing arithmetic operations over encrypted

data. The results remain encrypted with decryption

being the last step of the computing process. The data

can be therefore computed or analysed safely without

the possibility of unauthorized access to data or the

intermediate results. This makes it especially suitable

for the analysis of sensitive information, such as

patient health records. Besides healthcare, areas of

Puskaric, M.

A Framework for Federated Analysis of Health Data Using Multiparty Homomorphic Encryption.

DOI: 10.5220/0012753900003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 661-667

ISBN: 978-989-758-709-2; ISSN: 2184-7711

661

application include cloud computing, finance, the

Internet of Things (IoT), and more. Arithmetic

operations supported are addition and multiplication,

from which other operations, i.e. subtraction and

division can be derived. Secure computation and

exchange of information within the federated analysis

framework is enabled through multi-party computing

algorithms, where parties have to collectively

compute the critical security functions such as shared

encryption key generation or the distributed result

decryption. Some of the challenges with applying HE

include the computational overhead in data

processing and the complexity of the data analysis

algorithms that need to be rewritten for the efficient

use of HE.

HE applications and privacy-preserving federated

data analysis are central points of this research. An

overview of the related work is given in section 2,

followed by a description of the proposed federated

analysis framework and HE algorithms used. Finally,

data analysis examples with implementation and

workflow descriptions are presented and peer-

reviewed research studies, primarily conducted using

the centralized analysis approach, were successfully

reproduced. The presented federated data analysis

framework is derived from the use cases from the EU

project ORCHESTRA (ORCHESTRA Cohort, n.d.)

whose plan is to create a Pan-European cohort for the

conduct of prospective and retrospective studies to

improve the prevention and treatment of COVID-19.

2 RELATED WORK

Most federated data analysis frameworks are

designed to operate in a star topology where all data

sources share intermediate results with the central

server. There are, however, reports on decentralised

layouts, which are developed or proposed to address

various issues during analysis, not necessarily related

to data privacy or security. (Wainakh et al., 2020)

investigates potential benefits of hierarchical

federated learning, such as no direct access from the

central server to the data providers. (Hosseinalipour

et al., 2020) describes the term fog computing, an

approach for performing a computation in a

heterogeneous network environment to prevent

network overload, where devices don’t have to be

connected to the central server and can provide

computational resources. Moreover, parameter

aggregation can be done on a middle layer before

sending results to the central node in the case of

federated learning. (Hosseinalipour et al., 2022)

presents another example of a distributed machine

learning model to connect a large number of devices

with various properties, such as limited uplink

transmission and communication protocol. With the

advent of HE, it became possible to perform basic

arithmetic operations (e.g. addition, subtraction,

multiplication) over the encrypted data. (Froelicher et

al., 2021) reports using secure multi-party

computation for conducting biomedical studies. The

developed system requires all parties to be

interconnected and is capable of exchanging and

processing only encrypted information. A single party

cannot decrypt the study’s results at any point. In

addition, the model has a collective key switching

feature implemented, which allows results to be

decrypted only by a querier’s secret key. (Sav et al.,

2021) is another example of the secure multi-party

computation suitable for neural network training,

which is network topology agnostic in the context that

parties can be arranged into any network topology.

Furthermore, all parties are foreseen as data owners

whose intermediate updates exchanged during the

training process remain encrypted. Because of the

HE, the last two examples add computational

overhead to the process, and adding a new server to

the model requires adjustments for all parties. (Blatt

et al., 2020) reports the application of HE on genome-

wide association studies. R DataSHIELD (Marcon et

al., 2021) is a tool for privacy-preserving distributed

data analysis, well known in the area of clinical data

analysis. Statistical operations are performed at the

data source, where a person or a group performing the

analysis receives only summary parameters or a final

result. From the network topology point of view, R

DataSHIELD is designed to work in a star topology.

3 FEDERATED ANALYSIS

FRAMEWORK

The proposed federated data analysis framework and

the communication flow are depicted in Figure 1. The

data sources are depicted as hospitals that

communicate only with their central nodes, sharing

only encrypted information with intermediate results.

Furthermore, hospitals are isolated from the

researcher as well as other central nodes and

underlying hospitals. Thus, the researcher does not

contact the hospitals directly. The framework reflects

the data infrastructure from the ORCHESTRA

project, where three national hubs (central nodes)

provide access to data delivered by the underlying

data sources. The number of data sources assigned to

each national hub varies which has also been

SECRYPT 2024 - 21st International Conference on Security and Cryptography

662

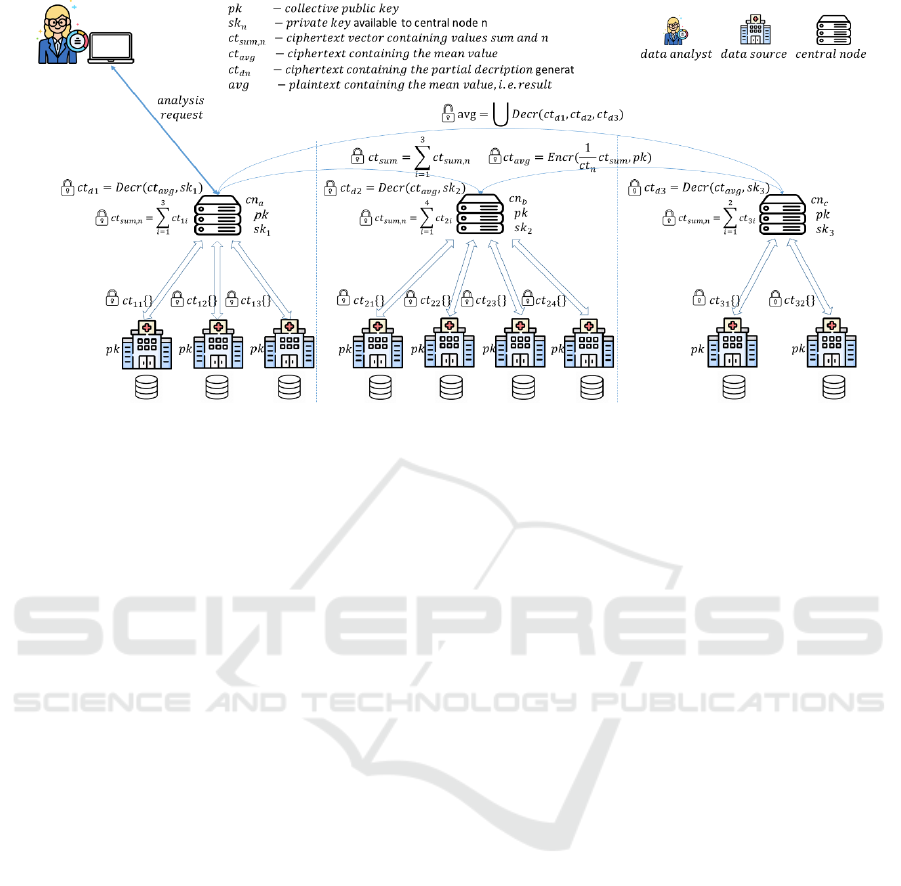
Figure 1: Federated data analysis framework with the communication workflow for computing the mean value.

considered in the presented framework. The

advantage of applying HE algorithms is that the data

sources only need to provide a connection to the

central node (national hub) for handling encrypted

data analysis requests without outsourcing their data

and exposing the intermediate results that might cause

sensitive information breaches.

The information between the clusters, as well as

between the clusters and the data sources, is

exchanged in an encrypted way using HE algorithms.

Besides encrypted data processing, the latter allows

multi-party computing where all involved parties

collaborate in cryptographic processes, such as

generating shared public keys and distributed

decryption of a ciphertext. In this framework, central

nodes collaborate to create the shared public keys

using their respective secret key shares. Central nodes

share public keys with their data sources for

application to their data. The data never leaves the

data source during the analysis. At the end of the

analysis workflow, central nodes collaborate to

decrypt the ciphertext containing the result.

Compared to the frameworks presented in

(Froelicher et al., 2021) and (Sav et al., 2021), this

framework differs in that data sources remain hidden

behind their central nodes, with no direct interaction

across clusters. Furthermore, adding or removing a

data source to the framework affects only the

involved central node and introduces no overhead

associated with generating new shared homomorphic

keys. Adding or removing a central node would affect

the whole framework, which includes recreating the

shared keys.

3.1 Homomorphic Encryption

Workflow

The term crypto-context is used throughout the

article, which denotes the selected encryption scheme

and configured encryption parameters. The HE keys

can be grouped into two categories: secret keys which

are never shared with other nodes, and public keys

which are shared with other nodes in the framework.

The latter comprises a public key for encrypting the

vector containing data, an evaluation rotation key for

accessing the values at the specific index of the

encrypted vector, and an evaluation multiplication

key for reducing the amount of noise in the ciphertext

caused by homomorphic multiplication operations.

The data analysis and the crypto-context

generation are initiated from one place, e.g. by the

researcher. A newly created crypto-context is sent to

one of the central nodes, which acts as a first contact

point and is also in charge of forwarding the crypto-

context to the rest of the central nodes. This is

followed by the message exchange between three

central nodes with respective secret key shares

𝑠𝑘



, 𝑠𝑘



and 𝑠𝑘



, who collaborate to create a public

key 𝑝𝑘 , evaluation multiplication key 𝑚𝑘 and

evaluation rotation key 𝑟𝑘. These keys can be shared

with data sources. Secret key shares on the other hand

remain stored on corresponding central nodes.

The number of communication rounds for

creating the shared public keys depends on the

number of involved parties, i.e. central nodes. For the

presented framework, up to 7 communication rounds

per shared key are necessary. In particular, 𝑝𝑘, 𝑟𝑘

and 𝑚𝑘 require 𝑛-1, 𝑛-1 and 2𝑛-1 communication

A Framework for Federated Analysis of Health Data Using Multiparty Homomorphic Encryption

663

rounds, respectively, where 𝑛 is the number of

involved parties. The data sources can now request

shared keys from their central nodes. Distributed

decryption requires all central nodes to collaborate

and use their secret key shares 𝑠𝑘



, 𝑠𝑘



and 𝑠𝑘



compute the partial decryptions which are then joined

into a final decryption, which is equivalent to the

plaintext of an analysis result.

HE algorithms allow basic arithmetic operations,

namely addition and multiplication. Subtraction can

be derived from addition without applying a special

algorithm. The division can be derived from

multiplication by applying a special approximation

algorithm. In the case of the presented framework, the

Goldschmidt iterative division algorithm

(Goldschmidt, 1964) as an approximation method is

used, represented by the equation (1), where 𝑥 is the

number for which the reciprocal is computed:

𝑥

1−(1−𝑥)

=(1+

(

1−𝑥

)





)





≈(1+

(

1−𝑥

)





)





(1)

and where crypto-context parameters implicitly

determine 𝑑 through a maximum number of

multiplication operations allowed.

The CKKS homomorphic encryption scheme for

approximate arithmetic (Cheon et al., 2017) is chosen

because it can be applied to real numbers and it

supports multi-party computing. All HE operations

used in the federated analysis workflows, including

multi-party algorithms, are supported by the CKKS

scheme and are implemented in the programming

library used for the framework development (Section

4). The crypto-context parameters (ciphertext

dimension and modulus in particular) are selected to

achieve the 128-bit level of security. The distributed

decryption is part of the multi-party algorithms

supported by the programming library. It is performed

only by central nodes as a last step of the data analysis,

where each node after computing partial decryption

using their respective secret key shares, performs a

fusion of the partial decryptions into a readable result

ready to be shared with the data analyst.

Each data source 𝑑𝑠



provides a harmonised

dataset in a CSV (Comma-Separated Values) format.

Before starting an analysis, 𝑑𝑠



has to request shared

keys 𝑝𝑘 and 𝑚𝑘 from the associated central node.

3.2 Data Analysis Workflows

3.2.1 Distributed Mean Value

Following is the workflow for finding the mean value

of the analysed dataset:

1. Data source 𝑑𝑠



reads the CSV file with the

individual patient information in a harmonised

format, for which the mean value is computed.

2. Data source 𝑑𝑠



computes the local sum and

encrypts the vector array of the result and the

number of individuals with the 𝑝𝑘. The created

ciphertext 𝑐𝑡



is then sent to the corresponding

central node.

3. Central nodes receive 𝑐𝑡



from the underlying

data sources, after which a local sum 𝑐𝑡

,

and

a local number of individuals 𝑐𝑡

,

are computed

by adding 𝑐𝑡



, followed by the addition between

central nodes to find the overall sum 𝑐𝑡



and

the overall number of individuals 𝑐𝑡



. This step

is done entirely using HE algorithms.

4. Since the average value is computed by

multiplying the 𝑐𝑡



with the reciprocal value

of 𝑐𝑡



, the Goldschmidt division (1) is used,

together with shared keys 𝑟𝑘 and 𝑚𝑘. The 𝑐𝑡



first scaled to a range of [0,2]. The maximum

number of individuals must be set in advance to

find the scaling factor. The Goldschmidt

algorithm runs in seven iterations due to

predefined parameters of the crypto context.

Furthermore, seven iterations have proven to be

sufficient for the accurate result. The result is

then rescaled back.

5. The reciprocal value is multiplied by the sum to

get the ciphertext 𝑐𝑡



with the mean value.

6. Distributed decryption of 𝑐𝑡



between central

nodes takes place.

3.2.2 Survival Analysis

The survival analysis, in this case, is computed using

the Kaplan-Meier estimator, which is presented by

the equation (2):

𝑆



(

𝑡

)

∏

(1 −









)

,





(2)

where 𝑡



is a time when at least one event happened,

𝑑



is the number of events that occurred at time 𝑡



and 𝑛



is the number of individuals known to have

survived up to time 𝑡



Given that all data sources have a harmonised

dataset in a CSV format where each patient is

described with the following values: patient ID, time

SECRYPT 2024 - 21st International Conference on Security and Cryptography

664

and survival event, the workflow for the survival

analysis is conducted as follows:

1. Data source 𝑑𝑠



reads the CSV file with the

individual patient information used for the

survival analysis.

2. Data source 𝑑𝑠



computes the new vector with

time point, number of negative outcomes and

number of censored events (for each time point).

In addition, the vector also contains the number

of patients present in the CSV file. The resulting

vector is encrypted using 𝑝𝑘 . The created

ciphertext 𝑐𝑡



is then sent to the central node.

3. Central nodes receive 𝑐𝑡



from the underlying

data sources, after which they are added into one

ciphertext 𝑐𝑡



4. Distributed decryption of 𝑐𝑡



between central

nodes takes place.

5. This step is performed by the data analyst: values

from the decrypted vector are used to compute

the number of patients per time point and finally,

the survival rate using the Kaplan-Meier

estimator presented by (2). At this point, the

result can be visualised.

The workflow for the survival analysis is similar

to those described in (Froelicher et al., 2021).

4 EXPERIMENTAL SETUP

The HE part of the federated analysis framework is

built using OpenFHE (Al Badawi et al., 2022), a C++

library that provides implementations of fully

homomorphic encryption schemes. The rest of the

framework is developed in C++ and with the ZeroMQ

library (Hintjens, 2013) for message exchange

between the nodes. The structure of the network

messages that are sent between the parties comprises

a header section for sorting the messages, and a body

section containing the data to be sent. Furthermore,

the experiments were conducted using the ‘tc’ tool in

Linux to simulate a network latency of 20 ms and a

bandwidth of 1 Gbit/s. The framework prototype was

compiled and tested on a single machine with a Linux

operating system and the following hardware: 2x

AMD EPYC 7261 8 core processor, 125 GiB of

working memory, and 128 GB of SSD storage. All

parties in the analysis framework communicate using

TCP/IP sockets. It is important to point out that

OpenFHE already provides various approximation

algorithms based on Chebyshev polynomials, such as

a reciprocal or a sigmoid function. This paper

however reports the implementation of the previously

mentioned Goldschmidt algorithm for finding the

reciprocal value of a given number. The data used for

the analysis are coming from the study reported in

(Samstein et al., 2019).

Central node and data source have server and

client components. Before starting the shared keys

generation or data analysis, server components should

be up and running and listening to incoming

connections. Client components initiate the outgoing

connection based on the input received by the server

component. The researcher is provided with an

associated client component to establish a connection

with one of the central nodes that serves as a main

contact point, which in this case is a central node 𝑐𝑛



Before execution of the analysis or HE keys

generation, the availability of all the central nodes is

checked.

5 RESULTS

Compared with the centralised and non-encryption

analysis methods, the following processes need to be

taken into concern: crypto-context distribution, HE

keys generation, data encryption, distributed

decryption, message exchange and homomorphic

arithmetic operations. These require additional

computation and storage resources, thus representing

a time overhead. For example, better performance can

be achieved by manually reducing noise in the

ciphertext generated by multiplication operations.

Both data analysis examples show that analysis data

does not have to leave the data source, and all

intermediate results are shared only as ciphertexts.

Furthermore, communication with data sources is

done only through central nodes, which makes them

hidden from other parties in the framework. By using

data from the study presented in (Samstein et al.,

2019), the obtained results are identical to those

obtained through a centralized analysis approach.

Key generation operation includes serialising keys

and saving them into separate files for later use.

Subsequent data analysis operations therefore do not

require key generation. The data analysis workflows

were tested on 9 data sources unevenly distributed

among 3 central nodes, as displayed in Figure 1. Each

data source had access to a different number of data

items, where the total number was 1662.

The workflow for computing the distributed mean

value of the TMB (Tumor Mutational Burden)

variable was tested first. Figure 2 shows the share of

key generation, data analysis and distributed

decryption per central node in the overall wall time.

The analysis time overhead is mainly caused by the

Goldschmidt algorithm and its loop composed of

multiple homomorphic multiplication operations.

A Framework for Federated Analysis of Health Data Using Multiparty Homomorphic Encryption

665

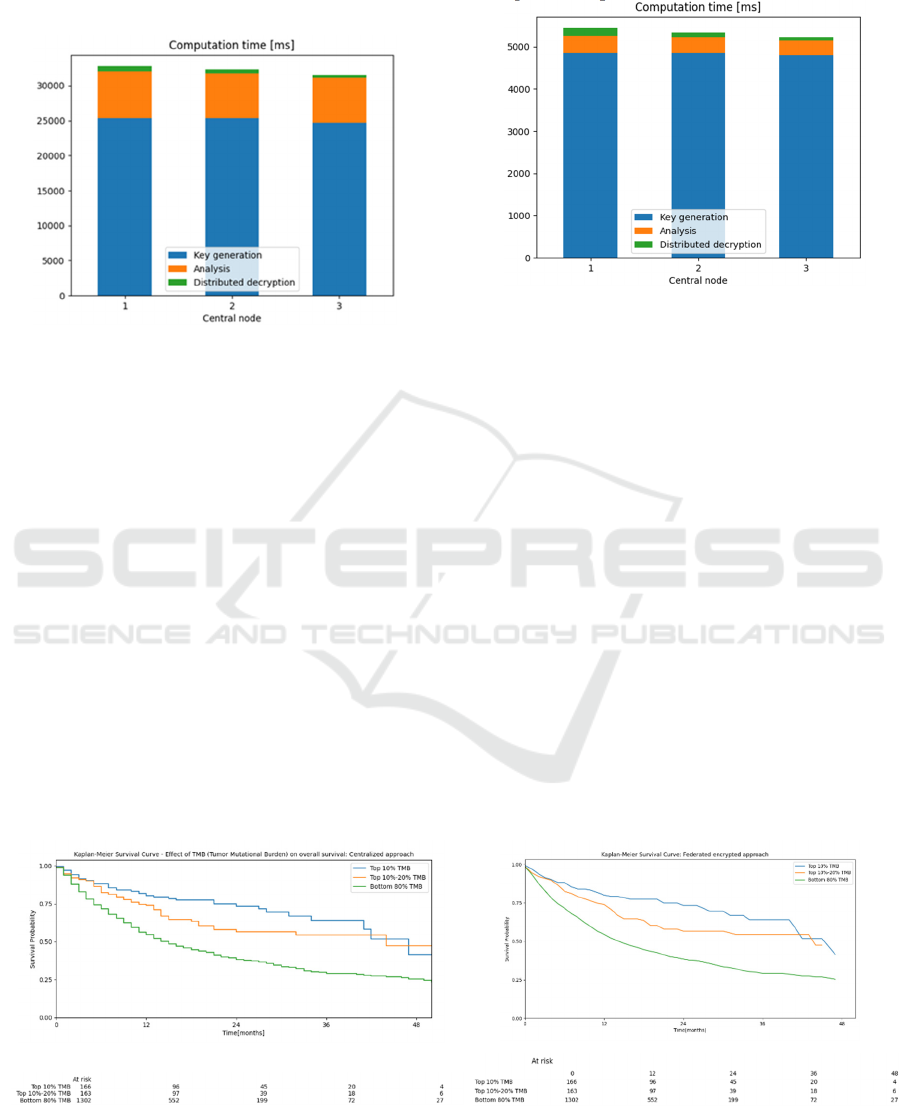
The algorithm is iterated seven times inside the loop.

The obtained result is 11.9692 and it does match the

one obtained through the centralized analysis

approach.

Figure 2: Wall time for the federated encrypted mean value

analysis.

The same setup was used for testing the survival

analysis workflow, the total number of data items or

patient records was again 1662. The analysis was

conducted on the same subset of data as in the original

study. Figure 3 shows the comparison of the results

between centralized and federated encrypted analysis,

which do match. The share of key generation, data

analysis and distributed decryption per central node

in the overall wall time is presented in Figure 4. The

measured wall time covers steps 1 to 4 from the

survival analysis workflow. The wall time for step 5

was not measured, as it was not done by the data

analyst after the distributed decryption.

The wall time for the distributed key generation is

longer for the distributed mean value analysis due to

the higher multiplicative depth setting in the crypto-

context configuration necessary to perform multiple

instances of the homomorphic multiplication

operation in the division algorithm. Survival analysis,

on the other hand, does not require homomorphic

multiplication operations.

Figure 3: Wall time for the federated encrypted survival

analysis.

6 CONCLUSION

This work presents a framework suitable for the

federated analysis of sensitive health data.

Decentralised network topology allows for creating

trust domains composed of a central node and

multiple data sources. Presented workflows for

computing mean value and survival analysis using the

Kaplan-Meier estimator demonstrate that

intermediate results do not have to be shared with

other parties in plaintext format. Instead, they are

encrypted and further computed using HE algorithms.

The decryption process is done at the very end of the

analysis process in a distributed way, requiring all

central nodes to collaborate. Finally, the obtained

centralized and federated encrypted analysis results

are identical.

Figure 4: Survival analysis results comparison between centralized (left) and federated encrypted (right) approach.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

666

7 FUTURE WORK

A preliminary step towards future work will be further

optimisation of the HE crypto-context parameters that

would reduce the analysis time overhead. Afterwards,

alternatives to distributed decryption will be explored,

such as key switching, where the result ciphertext gets

re-encrypted so that it only can be decrypted with a

secret key owned by the researcher. The final objective

in the presented future work plan is the implementation

of regression analysis workflow to support machine

learning algorithms that are running in multiple epochs

and iterations. This increases noise in the ciphertext

due to HE multiplication, requiring ciphertext

refreshing or bootstrapping (Micciancio & Polyakov,

2021) to reduce the amount of noise in the ciphertext

and allow subsequent operations and decryption. In a

multi-party setting, this activity has to be done

collaboratively by all central nodes, which presents an

additional step in the analysis workflow.

ACKNOWLEDGEMENTS

This work was supported by the ORCHESTRA

project, which has received funding from the

European Union’s Horizon 2020 research and

innovation programme under grant agreement No

101016167.

REFERENCES

Hansen, J., Wilson, P., Verhoeven, E., Kroneman, M.,

Kirwan, M., Verheij, R., & van Veen, E. B. (2021).

Assessment of the EU Member States' rules on health

data in the light of GDPR.

Zhu, L., Liu, Z., & Han, S. (2019). Deep leakage from

gradients. Advances in neural information processing

systems, 32.

Yang, H., Ge, M., Xue, D., Xiang, K., Li, H., & Lu, R.

(2023). Gradient Leakage Attacks in Federated

Learning: Research Frontiers, Taxonomy and Future

Directions. IEEE Network.

Naehrig, M., Lauter, K., & Vaikuntanathan, V. (2011). Can

homomorphic encryption be practical? Proceedings of

the 3rd ACM Workshop on Cloud Computing Security

Workshop.

Wainakh, A., Guinea, A. S., Grube, T., & Mühlhäuser, M.

(2020, September). Enhancing privacy via hierarchical

federated learning. In 2020 IEEE European Symposium

on Security and Privacy Workshops (EuroS&PW) (pp.

344-347). IEEE.

Hosseinalipour, S., Brinton, C. G., Aggarwal, V., Dai, H.,

& Chiang, M. (2020). From federated to fog learning:

Distributed machine learning over heterogeneous

wireless networks. IEEE Communications Magazine,

58(12), 41-47.

Orchestra Cohort. (n.d.). Project. Retrieved January 10,

2024, from https://orchestra-cohort.eu/work-packages/

Hosseinalipour, S., Azam, S. S., Brinton, C. G., Michelusi,

N., Aggarwal, V., Love, D. J., & Dai, H. (2022). Multi-

stage hybrid federated learning over large-scale D2D-

enabled fog networks. IEEE/ACM transactions on

networking, 30(4), 1569-1584.

Froelicher, D., Troncoso-Pastoriza, J. R., Raisaro, J. L.,

Cuendet, M. A., Sousa, J. S., Cho, H., ... & Hubaux, J.

P. (2021). Truly privacy-preserving federated analytics

for precision medicine with multiparty homomorphic

encryption. Nature communications, 12(1), 5910.

Sav, S., Pyrgelis, A., Troncoso-Pastoriza, J. R., Froelicher,

D., Bossuat, J. P., Sousa, J. S., & Hubaux, J. P. (2021,

January). POSEIDON: Privacy-Preserving Federated

Neural Network Learning. In 28Th Annual Network

And Distributed System Security Symposium (Ndss

2021) (No. CONF). INTERNET SOC.

Blatt, M., Gusev, A., Polyakov, Y., & Goldwasser, S. (2020).

Secure large-scale genome-wide association studies

using homomorphic encryption. Proceedings of the

National Academy of Sciences, 117(21), 11608-11613.

Marcon, Y., Bishop, T., Avraam, D., Escriba-Montagut, X.,

Ryser-Welch, P., Wheater, S., ... & González, J. R.

(2021). Orchestrating privacy-protected big data

analyses of data from different resources with R and

DataSHIELD. PLoS computational biology, 17(3),

e1008880.

Goldschmidt, R. E. (1964). Applications of division by

convergence (Doctoral dissertation, Massachusetts

Institute of Technology).

Cheon, J. H., Kim, A., Kim, M., & Song, Y. (2017).

Homomorphic encryption for arithmetic of approximate

numbers. In Advances in Cryptology–ASIACRYPT 2017:

23rd International Conference on the Theory and

Applications of Cryptology and Information Security,

Hong Kong, China, December 3-7, 2017, Proceedings,

Part I 23 (pp. 409-437). Springer International

Publishing.

Al Badawi, A., Bates, J., Bergamaschi, F., Cousins, D. B.,

Erabelli, S., Genise, N., ... & Zucca, V. (2022,

November). Openfhe: Open-source fully homomorphic

encryption library. In Proceedings of the 10th

Workshop on Encrypted Computing & Applied

Homomorphic Cryptography (pp. 53-63).

Hintjens, P. (2013). ZeroMQ: messaging for many

applications. " O'Reilly Media, Inc.".

Samstein, R. M., Lee, C. H., Shoushtari, A. N., Hellmann,

M. D., Shen, R., Janjigian, Y. Y., ... & Morris, L. G.

(2019). Tumor mutational load predicts survival after

immunotherapy across multiple cancer types. Nature

genetics, 51(2), 202-206.

Micciancio, D., & Polyakov, Y. (2021, November).

Bootstrapping in FHEW-like cryptosystems. In

Proceedings of the 9th on Workshop on Encrypted

Computing & Applied Homomorphic Cryptography

(pp. 17-28).

A Framework for Federated Analysis of Health Data Using Multiparty Homomorphic Encryption

667