Detecting the Impact of Changes in Platelet Demand following the

Implementation of PRT Platelets in Canada

Linden Smith

and John Blake

1,2

Department of Industrial Engineering, Dalhousie University, Halifax, NS, Canada

Centre of Innovation, Canadian Blood Services, Ottawa, ON, Canada

Keywords: Change Point Detection, Synthetic Data, Forecasting.

Abstract: This paper describes tools to detect and estimate demand shifts for platelet products, through inventory

monitoring, following the implementation of pathogen reduction (PR) technology at a pilot site in the

Canadian Blood Services (CBS) network. A Statistical Process Control (SPC) framework was constructed to

detect change points in inventory signals. A discrete event simulation is used to generate synthetic data for

the inventory monitoring process. Both traditional forecasting and machine learning techniques were used to

increase sensitivity to change detection and reduce time to detection by supplying the SPC algorithm with

projected data. Experiments were run on data representative of changes in demand experienced at the pilot

production site. It was found that larger shifts in demand had a higher probability of detection and a lower

time to detection. Changes in demand, with an effect on the system larger than 10%, were almost always

detected. Detection time varies greatly depending on the level of the demand shift. Typically, shifts greater

than 25% have an average detection time of just over a week while shifts of less than 5% have an average

detection time of up to 25 weeks.

1 INTRODUCTION

In all Canadian provinces, excepting Quebec,

Canadian Blood Services is the sole agency

responsible for managing the blood supply chain.

CBS collects, produces, and distributes blood

products to over 400 hospitals. Before being released

for transfusion, products must be tested for the

presence of transmissible diseases and/or bacterial

contamination.

In this paper we consider two blood products,

pooled and apheresis platelets, following the

introduction of technology to reduce bacterial

contamination. In Canada, a unit of pooled platelets

is a combination of buffy coat platelets derived from

five different donors, all of whom have the same

blood type. Apheresis platelets are collected from a

single donor. A single component is removed, while

the remaining components are returned to the donor.

Because platelets must be held at 37

C for maximum

clinical efficacy, bacterial contamination, though

rare, is possible. Thus, all platelet products, in

Canada and elsewhere, have a regulated shelf-life. At

the start of this study, platelets had a maximum shelf-

life of 7 days.

At that time, platelet units in Canada were tested

for bacterial contamination, using the BAC-T Alert®

system, a non-destructive testing system that rapidly

incubates an aliquot from production units. The risk

of transfusing a bacterial contaminated unit was

estimated at less than 1 in 1,000 with this technology.

However, CBS introduced Pathogen Reduction

Technology (PRT) for pooled platelet processing to

reduce further the chance of transfusion related

infections. PRT functions by combining a blood

product with a light sensitive compound and exposing

the mixture to ultraviolet light. The process causes

mis-links in the DNA of pathogens in the blood

product, preventing the organism from reproducing

and effectively sterilizing the product (Estcourt et al.,

2018).

While there are significant benefits to PRT

treatment, it is known that treated units have a lower

platelet count than untreated units (Estcourt, et al.,

2017). Thus, there was potential that an increased

number of units used would be required to achieve the

same dose-response in patients who might have

otherwise been transfused with non-PRT platelets.

Additionally, there was uncertainty regarding the

Smith, L. and Blake, J.

Detecting the Impact of Changes in Platelet Demand following the Implementation of PRT Platelets in Canada.

DOI: 10.5220/0012718300003758

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2024), pages 229-236

ISBN: 978-989-758-708-5; ISSN: 2184-2841

229

preference for a pathogen reduced platelet product

amongst prescribing physicians.

1.1 Objective

This study provides a method for evaluating tools to

detect and estimate demand shifts for platelet

products following the implementation of PR

technology at a pilot site in the CBS network.

2 LITERATURE REVIEW

Research on platelet management typically focuses

on reducing waste and shortage. Often, this involves

the selection of an appropriate platelet ordering policy

and/or managing demand. Research in demand

analysis can be categorized by method, including

forecasting, simulation, and integrated Operations

Research (OR) methods.

2.1 Forecasting Research

Forecasting methods improve inventory metrics by

predicting demand. Forecasting methods have been

used throughout the history of research on blood

product inventory management, but recently there has

been interest in forecasting as an application for

machine learning methods.

Silva Filho (2012) used an ARIMA model to

forecast demand across regional supply chain. A tool

was created that could be used by managers in

different regional blood centres. Lestari (Lestari,

Anwar, Nugraha, & Azwar, 2017) used

autoregressive methods to predict demand for

different blood products, but found that a simple

moving average performed best.

Khaldi (2017) applied Artificial Neural Networks

(ANN) to forecast demand for products at a regional

blood centre level. ARIMA models were used as a

benchmark. The performance of the ANN models

was found to far exceed that of the ARIMA models.

However, ARIMA models produced results that were

more interpretable for managers.

Shih (2019) compared time-series methods to

machine learning. ARIMA, Exponential Smoothing

Models, and Holt-Winters were compared with

ANNs and Multiple Regression. Shih found that the

time-series methods performed similarly, while

Multiple Regression outperformed the Artificial

Neural Network. When the time-series methods were

compared to machine learning, the results were

inconclusive, with different time series models and

regressions performing better on some data sets.

2.2 Simulation Methods

Simulation is amongst the most popular technique for

modelling and evaluating blood product inventory.

Atkinson (2012) used a hospital simulation to

determine trade offs between cost and transfusion

efficacy when demand is close to, or greater than,

supply.

Asllani (2014) designed a decision support system

which simulated the collections and demand for

apheresis platelets in a regional blood centre. It was

found that collecting fewer A+ apheresis platelets,

and not collecting on weekends reduced waste by 7%.

Blake (2017) examined the inventory impact of

increasing the shelf-life of platelets. Different

ordering polices were required to reduce waste for

each of the values of shelf-life, but significant

improvements were found for all cases.

2.3 OR Methods

In addition to forecasting and simulation, several

works related to platelet inventory management using

techniques such as stochastic dynamic programming

(SDP), approximate dynamic programming (ADP),

and integer stochastic programming (ISP) can be

found in the literature.

Haijema (2007) created a Markov decision

process formulation for platelet ordering policies at

the regional level. A simulation approach was used to

search for the single best ordering policy. It was

found that the simulation provided near optimal

results in both the downsized and full-scale problems.

Civelek (2015) follows much the same structure as

Haijema (2007) and Van Dijk (2009) with the

addition of a critical level protection policy.

Abdulwahab (2014) used both linear

programming and approximate dynamic

programming to develop a model of a single hospital

and blood bank. The approach was able to find an

optimal solution without downsizing. Similarly,

Gunpinar (2015) used a stochastic integer

programming model to model hospital level

inventory to find an optimal solution.

Guan (2017) analyzed factors in platelet usage at

the hospital level to determine factors influencing

demand. These included units transfused in the

previous days/weeks, census data, and complete

blood count for inpatients.

2.4 Research Summary

Previous work on blood product inventory

management has focussed on decision support with

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

230

the goal of reducing waste and shortage. Inventory

monitoring is an important component of these

models. However, it is performed with the

assumption that the properties of demand do not have

change points. Thus, there is a significant gap in the

research on inventory monitoring itself, and the

transient component of changes in the blood supply

chain.

METHOD

In this study we employ Statistical Process Control

(SPC) to monitor inventory at a CBS production

centre following a change in product. A discrete event

simulation is used to generate synthetic data for the

inventory monitoring process, since data

representative of possible demand changes did not

exist. Forecasting methods, using both traditional and

machine learning techniques, are employed to

increase sensitivity to change detection and reduce

time to detection by supplying expected future data

points.

3.1 Control Charts

Standard control charting, was used to compare the

values of points in a series, ordered by time, against

established process properties.

In the problem case, both pooled and apheresis

platelets are available to satisfy patient requirements.

Apheresis units, which are more expensive than

pooled platelets, are reserved for

immunocompromised patients. Apheresis platelets

may be substituted for pooled platelets, but pooled

platelets are not substituted for apheresis demand.

This complicates the problem, since pooled and

apheresis platelets may be affected differently by

changes in demand, and some changes will present

more in one product than the other. To account for

this, both the pooled and apheresis inventory streams

were monitored in this project.

3.2 Data Generation

Since PRT platelets are a new product, no suitable

data existed to evaluate change point detection

methods. Thus, a discrete-event simulation was built

to create inventory data representative of changes in

demand. The simulation is comprised of three top-

level components: collections, inventory, and

demand. The relationships between the system

elements are illustrated in Figure 1. Collections are

created daily, according to a Poisson distribution, and

placed in inventory. The shelf-life of collected units

on arrival to inventory is decreased by some number

of days to simulate the time required for production

and testing processes. Demand is created daily, and

inventory is allocated to fill it. Remaining inventory

is aged one day or, if it has no remaining shelf-life,

outdated. The process then repeats for some number

of days.

Figure 1: Inventory simulation framework. The simulation

generates artificial data for the change point detection

algorithm.

The simulation allocates inventory to fill demand

using a matching heuristic based on the steps taken by

CBS decision-makers when filling orders:

1. Exactly match apheresis inventory with

apheresis demand, with priority given to units

with lowest remaining shelf-life.

2. If there is unsatisfied demand for a specific

apheresis unit, substitute a compatible apheresis

unit, with priority given to units with the lowest

remaining shelf-life.

3. Check the shelf-life of apheresis inventory. If

there are any with a remaining shelf-life of 0

days, use them to fill compatible orders for

pooled platelets.

4. Exactly match pooled inventory with pooled

demand, with priority given to units with lowest

remaining shelf-life.

5. If there is unsatisfied demand for pooled

platelets which cannot be exactly matched,

substitute a compatible pooled unit with priority

given to units with the least remaining shelf-life.

Inventory is monitored continuously in the simulation

and a feedback controller is included to maintain a

stable inventory level. The controller reviews recent

collections, including those in inventory, but not

released for shipment, and determines the probability

they will meet demand over a short planning horizon.

If the probability is sufficiently low, collections are

increased in the following weeks. There is, however,

a limit to the effort the controller can exert,

representing the level of adaptability of the system.

Detecting the Impact of Changes in Platelet Demand following the Implementation of PRT Platelets in Canada

231

3.3 Enhancing Change Point Detection

with Local Forecasting

The time required to detect changes in a time series is

constrained by the rate of acquisition of new data. In

this study, data is collected daily, but analyzed

weekly to reduce noise due to day-to-day variation.

To increase the speed and quality of detection,

forecasting was used to supply the change point

detection algorithm with additional (anticipated) data

points. Linear Regression, ARIMA, Local

Regression, Generalized Additive Models (GAM),

and Random Forest methods were all evaluated.

4 DATA

The data used to populate the simulation comes from

a sample from a CBS production site for the 2019

calendar year. Summary statistics for platelet

inventory are shown below in Table 1.

Table 1: Daily inventory summary for the study region.

Blood

Type

Product

Type

Mean Daily

Inventory,

units

Daily

Inventory

Stand. Dev,

units

A+ Poole

56.99 16.02

A- Poole

4.98 3.28

B+ Poole

11.14 4.80

B- Poole

0.28 0.55

AB+ Poole

0.64 1.37

AB- Poole

0.00 0.00

O+ Poole

60.63 20.10

O- Poole

13.11 7.19

A+ Apheresis 13.00 5.51

A- Apheresis 2.88 2.31

B+ Apheresis 3.64 2.57

B- Apheresis 0.189 0.56

AB+ Apheresis 1.82 1.67

AB- Apheresis 0.14 0.49

O+ Apheresis 15.00 6.32

O- Apheresis 1.03 1.08

Table 2 below displays the inventory summary for

pooled and apheresis platelets.

Table 2: Daily inventory distribution.

Property Pooled

Inventory

Apheresis

Inventory

Mean 147.8 37.7

Standard Deviation

28.4 9.2

5 EXPERIMENTS

5.1 Validation

The simulation model was validated by comparing

simulation output to the parameters of the input data.

The daily inventory was extracted from the input data.

Daily inventory data was collected from the

simulation by using a long-term run of 10,000 days.

Results suggested that the simulation was able to

represent, adequately, the system under study.

(Results excluded for brevity.)

5.2 Synthetic Data

Two sets of data are generated by the simulation in

this study. The first evaluates the false positive

component of the detection accuracy metric, by

creating data with the same statistical properties as

the 2019 data.

The second set of evaluation data assesses the

false negative component of the detection accuracy

metric and the time to detection metric.

Changes in demand can be described by level,

type of function, and the probability they will assume

a value at a given time. See Table 3.

Table 3: Demand shift parameters.

F(t) Magnitude

step deterministic

linear stochastic

Example changes in demand are depicted below

in Figure 2. Note that linear changes in demand are

implemented as a regular increase across a time

period of four weeks.

Figure 2: Examples of different possible changes in

demand.

There are several ways in which demand may be

affected by the introduction of PRT platelets, and

while not all of them are necessarily equally likely,

access to simulation makes testing worthwhile. As a

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

232

result of PRT platelets replacing BAC-T bacterial

contamination detection there may be:

• An increase in pooled demand

• An increase in apheresis demand

• A transition of demand from pooled to

apheresis

5.3 Evaluation of Forecasting Methods

As noted, local forecasting was used to improve the

time to detection of a change by supplying the

detection algorithm with assumed future data points.

Forecasting methods, listed below, were tested on the

base model data to determine their effect of the

change point detection.

Table 4: Forecasting method performance and impact on

false detection rate.

Method

Base Case

MAPE, %

RMSE, units

of platelets

Base Case

False

Detection

Rate, %

No Forecasting -- -- 3.20

ARIMA 13.14 16.85 3.50

Linear Regressio

15.45 20.00 6.50

GAM – Local

Regression

16.64 21.90 31.50

GAM - Splines 14.35 18.57 4.90

Two forecasting accuracy metrics were used to

evaluate forecasting accuracy, along with false

detection rate: Mean Absolute Percentage Error

(MAPE) and Root Mean Squared Error (RMSE).

As can be seen in Table 4 the ARIMA model was

found to perform best according to the forecasting

accuracy metrics. Accordingly, for the case study,

ARIMA methods were used to supply the change

detection algorithm with additional data points.

5.4 Changes in Shelf-Life

After the implementation of PRT platelets, the

regulatory shelf-life of pooled platelets was reduced

from 7 days to 5 days for the period of time

considered in the case study. To account for the

change in approved shelf-life of PRT platelets the

shelf-life of pooled platelets was decreased by two

days in the simulation; apheresis platelets, which

were not pathogen reduced, continued to have a 7-day

shelf-life. Readers should note that subsequent to this

study, the regulatory shelf-life of PRT platelets in

Canada was extended to 7 days.

5.5 Overview of Experiments

Change point detection experiments in this study

were divided into 3 categories: single factor, two

factor, and 2

factorial. The first category, single

factor experiments, were used to investigate the effect

of a single type of demand change on inventory. Two

factor experiments follow the same structure but with

two types of demand change present. Finally, the 2

factorial experiments examine interaction among

demand change factors.

6 RESULTS

6.1 Single Factor Experiments

To evaluate the performance of detection methods

experiments were conducted on data with only a

single factor change. An example is shown below in

Figure 3 and Figure 4.

Figure 3: Change in demand and its effect on likelihood of

detection.

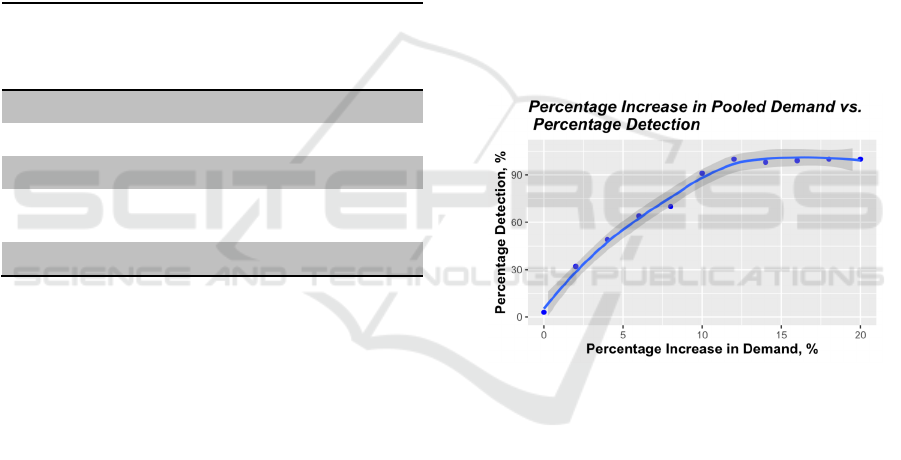
Figure 3 depicts the percentage of detections

when the level of increase in pooled demand is

changed in a deterministic step. These results indicate

that the chance of signal detection converges to 100%

when demand increases exceed 10%. The grey

shadow in the figure represents the confidence

interval for detection.

Figure 4 shows the mean time to detection for the

same single factor experiment. The mean time to

detection decreases as the level of increase in pooled

demand increases. The mean time to detection for a

2% increase is 23 weeks, while the mean time to

detection for a 20% increase is 6 weeks.

Detecting the Impact of Changes in Platelet Demand following the Implementation of PRT Platelets in Canada

233

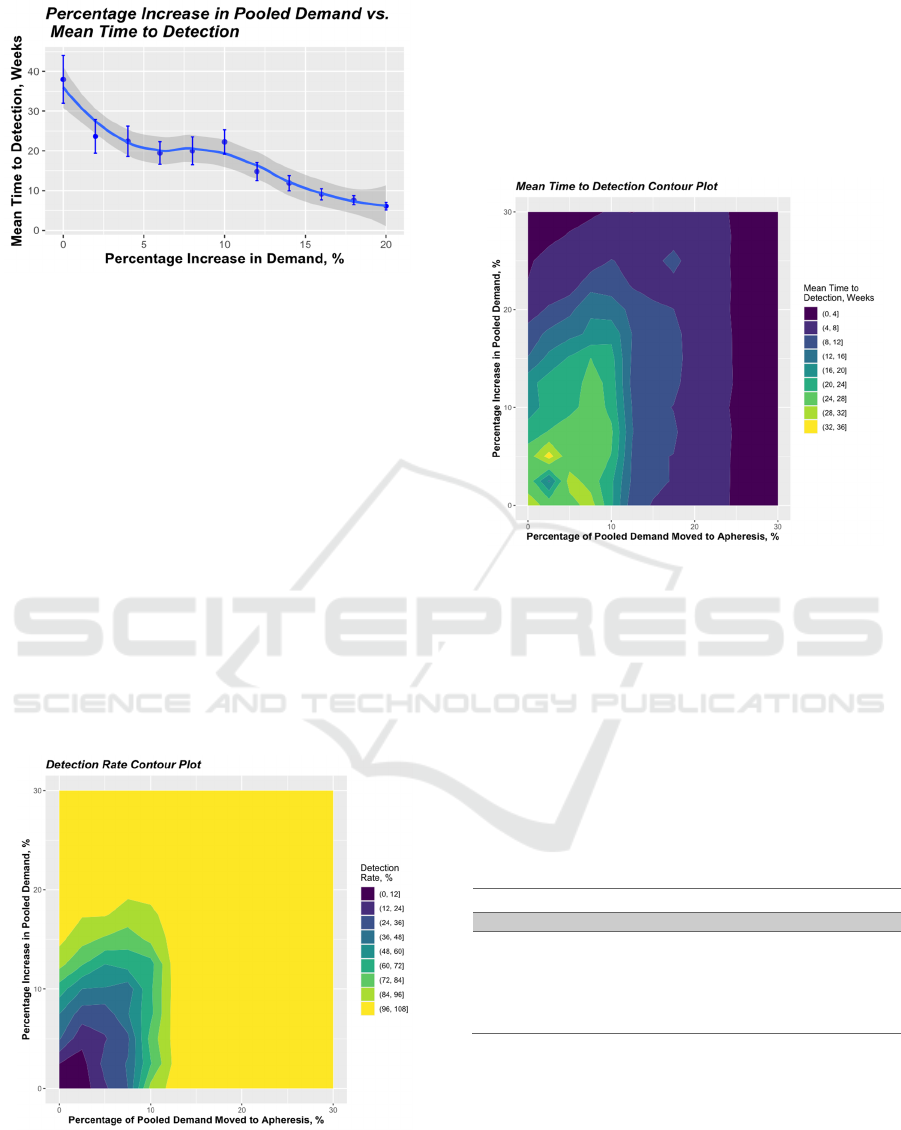
Figure 4: Change in demand and its effect on the time

required to detect the change.

Two Factor Experiments:

A concern for the blood supplier was that an increase

in the demand for pathogen-reduced pooled platelets,

to make up for the lower per unit yield, might be

accompanied by a migration of demand to apheresis

platelets. Thus, a set of experiments was performed to

examine the performance of detection methods to

demand changes exhibiting these patterns.

The detection rates for these experiments are

found in Figure 5. These results represent a step

change in both pooled demand and shift to apheresis

units. The contours indicate that the detection rate

converges to 100% for demand shifts between 10%

and 15%. It can also be observed that the effect of a

migration from pooled to apheresis is detected, at

lower levels, more often than the effect of an increase

in demand for pooled platelets is detected.

Figure 5: Contour plot of detection rate for change in pooled

demand accompanied by a shift from pooled to apheresis

units.

The mean time to detection for the multiple

demand shift experiment is displayed in Figure 6.

While there are anomalies, the mean time to detection

generally decreases as the magnitude of the demand

shift increases. These results are similar to, but less

favourable than, those detected during the single

factor experiments.

Figure 6: Contour plot of detection time for Contour plot of

detection rate for change in pooled demand accompanied

by a shift from pooled to apheresis units.

6.2 Multifactor Experiments

To ascertain the effect of different demand shift

parameters on performance, and the interaction of

factors, the change point detection algorithm was

applied to data with multiple demand factors under

the assumption of a 2

-factorial experiment. See

Table 5.

Table 5: Factor descriptions for 2

experiments.

Factor

1 2 3 4 5

increase

pooled

demand

increase

apheresis

demand

Transfer

of pooled

demand

apheresis

Step

increase

or linear

increase

Deterministic

or stochastic

The results of these experiments are displayed in

Figure 7 and Figure 8. Patterns are evident when

evaluating interactions of Factors 1-3 with Factors 4

(step vs. linear increase) and 5 (deterministic vs.

stochastic step). In Figure 7, the red line indicates the

mean percentage detections across experiments in

that group. The chart shows that a linear change, as

opposed to a step change, has a small negative effect

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

234

on both the probability of detection and time to

detection. Interestingly, a stochastic change in

demand is both more likely to be detected and is

detected more quickly than a deterministic change.

This may be because variance in an increasing

demand trend leads to more extreme values in

inventory that trigger detection rules in the SPC

method.

Figure 7: Detection rate for experiments factors 4 & 5: Step

vs. linear change and stochastic vs. deterministic change.

Figure 8: Mean time to detection for factorial level

experiments grouped using factors 4 & 5 Step vs. linear

change and stochastic vs. deterministic change.

The effect of a change in each factor on the results

of the 2

factorial experiments are shown in Table 6.

These indicate that the presence of all factors, except

a linear change in demand (Factor 4), increase the

detection rate and decrease time to detection. Factor

3, a shift of pooled demand to apheresis, has a

significantly larger effect on detection time than the

other factors. Since apheresis platelets make up only

32% of inventory, a small shift of demand from

pooled has a large effect on apheresis inventory.

Table 6: The effect of 2k experiment factors on detection

rate and time to detection.

Factor Effect on

Detection

Rate, %

Effect on

Detection

Time, Weeks

1 - Pooled

demand

increase

10.25 -3.54

2 – Apheresis

demand

increase

12.13 -4.80

3 – Pooled

demand to

apheresis

12.625 -8.19

4 – Step vs.

linear chan

-0.625 1.19

5 – Stochastic

vs. deterministic

4.375 -1.64

Evaluation of interaction effects proved that

presence of more than one type of increase generally

increases detection metrics. However, the presence of

a transfer of demand from pooled platelets to

apheresis platelets was found to have a small negative

impact on detection performance. Interaction terms

above 2

order were found to be insignificant.

6.3 Summary

Simulation results, shown in Table 7 give an

overview of estimated performance at different

demand shift levels.

Table 7: Summary of detection performance.

Change to

System, %

Mean

Detection

Rate, %

Mean

Detection

Time, Weeks

Detection

Time CI,

Weeks

1 to 5 72.8 25.12 14.43, 35.81

6 to 10 91.3 15.20 9.86, 20.54

11 to 15 98.4 8.83 5.19, 12.47

16 to 20 100.0 4.25 3.34, 5.16

21 to 25 100.0 1.38 1.26, 1.50

26 to 30 100.0 1.05 1.00, 1.10

Changes up to 5% change have a mean time to

detection of 25 weeks, while changes above 25%

have a mean time to detection of just over 1 week.

The overall detection rate converges to 100% when

the magnitude of change exceeds 10%.

Detecting the Impact of Changes in Platelet Demand following the Implementation of PRT Platelets in Canada

235

7 CONCLUSION

Standard SPC is effective in detecting shifts in

platelet demand. Results show that the key

performance metrics of detection rate and detection

time improve as the magnitude of the shift increases.

Forecast models were developed from established

families of forecasting methods to supplement the

SPC method. The models were evaluated using

historical data, base case runs of the inventory

simulation, as well as data representative of demand

shifts. The best performing method, ARIMA, was

incorporated into the SPC analysis to increase the

speed of data acquisition by providing additional data

points for the algorithm. Our model did not suggest

better performance using machine learning for

forecasting.

Changes in demand, with an effect on the system

larger than 10%, were always detected in our study.

Detection time varies greatly depending on the level

of the demand shift. Typically, shifts greater than

25% have an average detection time of just over a

week while shifts of less than 5% have an average

detection time of 25 weeks.

The results of this paper were used by the blood

agency to set parameters for monitoring the roll out

of PRT platelets in Canada, supplementing their

existing SPC methods.

REFERENCES

Abdulwahab, U., & Wahab, M. I. (2014). Approximate

dynamic programming modeling for a typical blood

platelet bank. Comput. Ind. Eng, 78, 259–270,.

doi:10.1016/j.cie.2014.07.017.

Asllani, A., Culler, E., & Ettkin, L. (2014). A simulation-

based apheresis platelet inventory management model.

Transfusion, 54, 2730–2735,. doi:10.1111/trf.12570.

Atkinson, M. P., Fontaine, M. J., Goodnough, L. T., &

Wein, L. M. (2012). A novel allocation strategy for

blood transfusions: Investigating the tradeoff between

the age and availability of transfused blood.

Transfusion, 52, 108–117,. doi:10.1111/j.1537-

2995.2011.03239.x.

Blake, J. T. (2017). Determining the inventory impact of

extended-shelf-life platelets with a network simulation

model. Transfusion, 57, 3001–3008,.

doi:10.1111/trf.14305.

Civelek, I., Karaesmen, I., & Scheller-Wolf, A. (2015).

Blood platelet inventory management with protection

levels. Eur. J. Oper. Res, 243, 826–838,.

doi:10.1016/j.ejor.2015.01.023.

Estcourt, L., Malouf, R., Hopewell, S., Trivella, M., Doree,

C., Stanworth, S., & Murphy, M. (2017). Platelet

transfusions treated to reduce transfusion-transmitted

infections for the prevention of bleeding in people with

low platelet counts. Cochrane Database of Systematic

Reviews(7).

Guan, L. (2017). Big data modeling to predict platelet usage

and minimize wastage in a tertiary care system. Proc.

Natl. Acad. Sci. U. S. A, 114, 11368–11373,.

doi:10.1073/pnas.1714097114.

Gunpinar, S., & Centeno, G. (2015). Stochastic integer

programming models for reducing wastages and

shortages of blood products at hospitals. Comput. Oper.

Res, 54, 129–141,. doi:10.1016/j.cor.2014.08.017.

Haijema, R., Wal, J., & Dijk, N. M. (2007). Blood platelet

production: Optimization by dynamic programming

and simulation. Comput. Oper. Res, 34, 760–779,.

doi:10.1016/j.cor.2005.03.023.

Khaldi, R., Afia, A. E., Chiheb, R., & Faizi, R. (2017).

Artificial neural network based approach for blood

demand forecasting: Fez transfusion blood center case

study. ACM Int. Conf. Proceeding Ser, Part F1294, 3–

8,. doi:10.1145/3090354.3090415.

Lestari, F., Anwar, U., Nugraha, N., & Azwar, B. (2017).

Forecasting demand in blood supply chain (case study

on blood transfusion unit. Lect. Notes Eng. Comput.

Sci, 2230, 764–767,.

Shih, H., & Rajendran, S. (2019). Comparison of Time

Series Methods and Machine Learning Algorithms for

Forecasting Taiwan Blood Services Foundation’s

Blood Supply. J. Healthc. Eng, 2019.

doi:10.1155/2019/6123745.

Silva Filho, O. C., & Saviano, G. (2012). A decision-

making tool for demand forecasting of blood

components. IFAC Proceedings Volumes, 45(6), 1499-

1504.

Van Dijk, N., Haijema, R., Wal, J., & Sibinga, C. S. (2009).

Blood platelet production: A novel approach for

practical optimization. Transfusion, 49, 411–420,.

doi:10.1111/j.1537-2995.2008.01996.x.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

236