Software Defect Prediction Using Integrated Logistic Regression and

Fractional Chaotic Grey Wolf Optimizer

Raja Oueslati

and Ghaith Manita

1,2

Laboratory MARS, LR17ES05, ISITCom, Sousse University, Sousse, Tunisia

ESEN, Manouba University, Manouba, Tunisia

Keywords:

Software Defect Prediction, Metaheuristic Algorithm, Grey Wolf Optimizer, Fractional Chaotic,

Logistic Regression.

Abstract:

Software Defect Prediction (SDP) is critical for enhancing the reliability and efﬁciency of software devel-

opment processes. This study introduces a novel approach, integrating Logistic Regression (LR) with the

Fractional Chaotic Grey Wolf Optimizer (FCGWO), to address the challenges in SDP. This integration’s pri-

mary objective is to overcome LR’s limitations, particularly in handling complex, high-dimensional datasets

and mitigating overﬁtting. FCGWO, inspired by the social and hunting behaviours of grey wolves, coupled

with the dynamism of Fractional Chaotic maps, offers an advanced optimization technique. It reﬁnes LR’s

parameter tuning, enabling it to navigate intricate data landscapes more effectively. The methodology in-

volved applying the LR-FCGWO model to various SDP datasets, focusing on optimizing the LR parameters

for enhanced prediction accuracy. The results demonstrate a signiﬁcant improvement in defect prediction

performance, with the LR-FCGWO model outperforming traditional LR models in accuracy and robustness.

The study concludes that integrating LR and FCGWO presents a promising advance in SDP, offering a more

reliable, efﬁcient, and accurate approach for predicting software defects.

1 INTRODUCTION

Software defect prediction (SDP) (Roman et al.,

2023) plays a pivotal role in enhancing the reliabil-

ity and efﬁciency of software development processes.

By anticipating potential defects early in the software

lifecycle, SDP aids in allocating resources effectively

and mitigating risks associated with software failures.

Despite its signiﬁcance, accurately predicting soft-

ware defects remains challenging, primarily due to

the complex and dynamic nature of software devel-

opment environments.

Among the array of machine learning (ML) tech-

niques, logistic regression (Acito, 2023) stands out as

one of the most utilized algorithms in SDP. Its pop-

ularity stems from its simplicity and interpretability.

Logistic regression is particularly adept at handling

binary classiﬁcation problems, like distinguishing be-

tween defect-prone and defect-free software modules.

It estimates the probabilities of classes, providing

clear insights into the likelihood of defects. This as-

pect is invaluable in SDP, where understanding the

risk of defects is as crucial as identifying their pres-

ence.

Logistic regression models typically rely on gradi-

ent descent for parameter optimization (Manita et al.,

2023). Gradient descent is a widely used approach

for minimizing the cost function, guiding the model

towards the most accurate predictions. However, this

method has limitations, especially in navigating com-

plex, multidimensional landscapes typical in SDP.

Gradient descent can get trapped in local minima, par-

ticularly with non-convex error surfaces, leading to

suboptimal parameter values and, consequently, less

accurate defect predictions.

Metaheuristic algorithms (Talbi, 2009) emerge as

a potent alternative to gradient descent for parame-

ter optimization in logistic regression models. Un-

like gradient descent, which incrementally adjusts pa-

rameters based on the local gradient, metaheuristics

explore the parameter space more broadly and cre-

atively. For instance, algorithms such as Genetic Al-

gorithm (GA) (Holland, 1992), Particle Swarm Op-

timization (PSO) (Eberhart and Kennedy, 1995), or

Grey Wolf Optimizer (GWO) (Mirjalili et al., 2014)

simulate natural processes to search for optimal or

near-optimal solutions. These methods excel in ﬁnd-

ing global optima in complex, irregular search spaces

Oueslati, R. and Manita, G.

Software Defect Prediction Using Integrated Logistic Regression and Fractional Chaotic Grey Wolf Optimizer.

DOI: 10.5220/0012704600003687

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2024), pages 633-640

ISBN: 978-989-758-696-5; ISSN: 2184-4895

633

by balancing exploration (searching new areas) and

exploitation (reﬁning known good areas).

By employing metaheuristic algorithms for pa-

rameter optimization, logistic regression models in

SDP can overcome some of the inherent limita-

tions of gradient descent. These algorithms en-

hance the model’s ability to navigate complex, high-

dimensional data landscapes, efﬁciently identifying

parameter combinations that yield the most accurate

predictions. This approach is particularly valuable in

handling the intricate and often non-linear relation-

ships present in software defect datasets, thereby im-

proving the robustness and reliability of SDP models.

To address these limitations, integrating meta-

heuristic algorithms like GA, PSO, and GWO has be-

come increasingly popular. These algorithms excel

in optimizing ML model parameters and feature se-

lection (Manita et al., 2012; Johnson et al., 2014;

Qasim and Algamal, 2018; Panda and Azar, 2021).

They enhance model performance, reduce complex-

ity, and ensure models effectively handle imbalanced

datasets, which is crucial in SDP scenarios.

This synergy between ML and metaheuristic op-

timization offers an advanced approach to SDP. By

combining the predictive capabilities of ML with

the optimization strengths of metaheuristics, the ﬁeld

moves towards more accurate, efﬁcient, and reli-

able defect prediction models. The LR-FCGWO ap-

proach is poised to offer signiﬁcant advantages in

SDP. By harnessing the enhanced search capabilities

of Fractional Chaotic maps, LR-FCGWO can outper-

form traditional algorithms in terms of accuracy and

computational efﬁciency. This approach is particu-

larly promising in addressing the challenges of high-

dimensional data and complex feature spaces com-

monly encountered in SDP.

This paper aims to explore the application of the

LR-FCGWO approach in the context of SDP. We seek

to investigate its prediction accuracy and computa-

tional efﬁciency performance, comparing it with ex-

isting metaheuristic algorithms. The remainder of this

paper is structured as follows. In the second sec-

tion, we present an overview of related work. In the

third section, we introduce the GWO algorithm. In

the fourth section, we deﬁne the proposed approach

FCGWO. In the ﬁfth section, we presents the LR-

FCGWO to predict software defects. In the sixth, we

evaluate the performance on the proposed approach

on different datasets. We conclude with a conclusion

and some future work.

2 RELATED WORK

In recent studies, metaheuristic optimization tech-

niques like Particle Swarm Optimization (PSO) have

been effectively applied to software defect prediction.

(Buchari et al., 2018) utilized Chaotic Gaussian PSO

(CGPSO) on 11 public benchmark datasets, show-

ing improved accuracy in the majority of cases. (Jin

and Jin, 2015) combined Quantum PSO (QPSO) with

a hybrid Artiﬁcial Neural Network (ANN) for pre-

dicting defects, demonstrating its efﬁcacy in correlat-

ing software metrics with fault-proneness, thus poten-

tially reducing maintenance costs and enhancing de-

velopment efﬁciency. Furthermore, (Wahono et al.,

2014) applied Genetic Algorithms and PSO for fea-

ture selection, alongside bagging to address class im-

balance, signiﬁcantly enhancing prediction accuracy

over traditional methods.

In (Panda and Azar, 2021), the Grey Wolf Opti-

mizer (GWO) is used for feature selection to enhance

bug detection classiﬁers. This method, applied to

multiclass bug severity classiﬁcation using MLP, LR,

and RF techniques, demonstrates improved prediction

accuracy on the Ant 1.7 and Tomcat datasets. The

study highlights the potential of GWO in advancing

software quality by efﬁciently identifying and classi-

fying bugs.

The authors in (Kang et al., 2021) demonstrate the

effectiveness of Harmony Search (HS) optimization

in Just-in-Time software defect prediction (JIT-SDP),

particularly for safety-critical maritime software. By

optimizing model parameters with HS, their approach

surpasses traditional models in predicting defects at

the commit level, showing improved accuracy and

recall rates across various datasets. This highlights

the potential of HS in enhancing software quality as-

surance through better management of class imbal-

ances and prediction performance. As reported in

(Elsabagh et al., 2020), the authors employ the Spot-

ted Hyena Optimizer algorithm with a multi-objective

ﬁtness function for defect prediction in cross-project

scenarios. This approach aims to improve classiﬁ-

cation accuracy where historical data is sparse and

varied. Testing on NASA datasets—JM1, KC1,

and KC2—the algorithm outperforms traditional data

mining techniques, achieving accuracy rates of 84.6%

for JM1, 92.0% for KC1, and 82.4% for KC2, high-

lighting its effectiveness in defect prediction.

In (Niu et al., 2018), the study introduces an

adaptive, multi-objective Cuckoo Search algorithm

aimed at enhancing defect prediction accuracy by op-

timizing multiple objectives and adaptively adjust-

ing dataset ratios to balance module sizes. This ap-

proach outperforms traditional defect prediction mod-

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

634

els, with simulations conﬁrming its superior accuracy

in defect prediction. The authors in (Zhu et al., 2021)

introduce EMWS, a feature selection algorithm com-

bining Whale Optimization Algorithm (WOA) and

Simulated Annealing (SA) for software defect pre-

diction. This method signiﬁcantly improves predic-

tion accuracy by effectively reducing irrelevant and

redundant features, showcasing EMWS’s efﬁcacy in

enhancing model performance.

As reported in (Zivkovic et al., 2023), the meta-

heuristic employed is a modiﬁed variant of the rep-

tile search optimization algorithm, HARSA (Hyper-

parameter Adjustment using Reptile Search Algo-

rithm). The results show its ability to enhance the

performance of the defect prediction model. In (Balo-

gun et al., 2020), metaheuristic search methods used

in this study for SDP in the context of Wrapper Fea-

ture Selection (WFS) include 11 state-of-the-art meta-

heuristics and two conventional search methods. The

goal is to compare the effectiveness of these meth-

ods in addressing the high dimensionality problem

and improving the predictive capabilities of models

in SDP.

The study (Raheem et al., 2020) investigate the

effectiveness of the Fireﬂy Algorithm (FA) and Wolf

Search Algorithm (WSA) in feature selection, com-

bined with Support Vector Machine (SVM) and Ran-

dom Forest (RF) classiﬁers for software bug predic-

tion. They use public software module datasets to

compare the performance of these machine learning

techniques. The authors in (Goyal and Bhatia, 2021)

explore the Lion Optimization-based Feature Selec-

tion (LiOpFS) method, which excels in choosing an

optimal feature subset from high-dimensional data,

tackling the Curse of Dimensionality. By ﬁltering out

only the most relevant features, LiOpFS signiﬁcantly

enhances classiﬁer performance and fault prediction

model accuracy.

3 GREY WOLF OPTIMIZER

(GWO)

The Grey Wolf Optimizer (GWO), as introduced in

(Mirjalili et al., 2014), stands out in the metaheuristic

landscape for its unique emulation of the social hi-

erarchy and hunting behaviour of grey wolves. This

algorithm encapsulates the wolves’ strategy of track-

ing, encircling, and ultimately attacking the prey. The

GWO algorithm is mainly characterized by incor-

porating the leadership and collaborative dynamics

within a wolf pack.

The mathematical model of the GWO initiates

with the encircling behaviour, described by:

⃗

D = |

⃗

C ×

⃗

(t) −

⃗

X(t)| (1)

⃗

X(t + 1) =

⃗

(t) −

⃗

A ×

⃗

D (2)

Here,

⃗

(t) denotes the prey’s position vector,

⃗

X(t) represents the position vector of a wolf, and t

signiﬁes the current iteration. The coefﬁcients

⃗

A and

⃗

C are computed as:

⃗

A = 2 ×⃗a ×⃗r

−⃗a (3)

⃗

C = 2 ×⃗r

(4)

where⃗a linearly decreases from 2 to 0 as iterations

progress, and⃗r

and⃗r

are random vectors within the

range [0, 1]. The social hierarchy within the wolf

pack is such that the alpha (α) wolf’s position is con-

sidered the current best solution. The beta (β) and

delta (δ) wolves follow the alpha, and the rest of the

pack (omega wolves) follow these leading members.

The phase of attacking the prey, the exploitation

phase, is marked by a reduction in the magnitude of ⃗a,

allowing the pack to converge towards the prey’s posi-

tion. This interplay between exploration (high ⃗a) and

exploitation (low ⃗a) is a testament to the algorithm’s

capacity to explore and exploit the search space adap-

tively, propelling it towards the optimal solution with

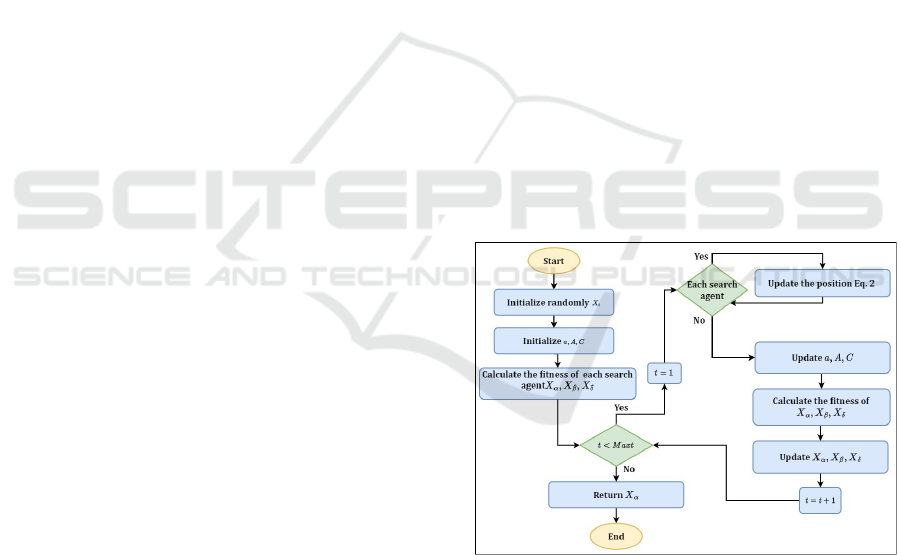
an effective balance. Figure 1 depicts the ﬂowchart of

the original GWO algorithm.

Figure 1: GWO Algorithm: A Detailed Flowchart.

4 PROPOSED APPROACH

FCGWO

Achieving a delicate balance between exploration and

exploitation is key in optimization algorithms to efﬁ-

ciently navigate complex search spaces. The Frac-

tional Chaotic Grey Wolf Optimizer (FCGWO) inno-

vatively combines fractional order chaos maps with

Software Defect Prediction Using Integrated Logistic Regression and Fractional Chaotic Grey Wolf Optimizer

635

the traditional GWO to balance exploration and ex-

ploitation in complex search spaces. This approach

uses the complex dynamics of chaos maps to evade

local optima, enhancing search efﬁciency. The fol-

lowing discussion will detail the mechanisms of frac-

tional chaos maps and FCGWO, illustrating its poten-

tial in solving various optimization challenges.

4.1 Fractional Chaotic

This research integrates three advanced fractional or-

der chaos maps (Wu and Baleanu, 2014; Wu et al.,

2014; ATALI et al., 2021) into the Grey Wolf Op-

timizer (GWO) to boost its performance by ad-

dressing local optima entrapment and optimizing the

exploration-exploitation balance, essential for reach-

ing optimal solutions.

• Fractional Logistic Map. Renowned for its in-

tricate dynamical properties, the fractional logis-

tic map is instrumental in enriching the diversity

within the search space, thereby facilitating more

extensive exploration.

• Fractional Sine Map. The map’s inherent peri-

odic nature is crucial in ensuring a comprehen-

sive scan of the solution space, enhancing the al-

gorithm’s thoroughness.

• Fractional Tent Map. This map introduces a

unique approach to traversing the optimization

landscape, offering novel pathways through the

search space.

The integration of these maps (detailed in Table

1) is an addition to the GWO algorithm and a strate-

gic incorporation of complex dynamical systems the-

ory into optimization. By leveraging the intricate be-

haviours of these chaotic systems, we aim to boost

the GWO algorithm’s ability to navigate and exploit

multidimensional search spaces effectively, leading to

more accurate, reliable, and quicker convergence to

optimal solutions across various scenarios.

Table 1: Fractional chaos maps with range 0 and 1.

Name Equation x(0) Parameters

Fractional Logistic x

k+1

= x

Γ(α)

∑

j=1

γ(k− j+α)

γ(k− j+1)

j−1

(1 − x

j−1

) 0.3 µ = 2.5, α = 0.3

Fractional Sine x

k+1

= x

Γ(α)

∑

j=1

γ(k− j+α)

γ(k− j+1)

sin(x

j−1

) 0.3 µ = 3.8, α = 0.8

Fractional Tent x

k+1

= x

Γ(α)

∑

j=1

0.3 µ = 1.9, α = 0.6

Γ(k− j+α)

Γ(k− j+1)

min((µ − 1)x

j−1

,µ − (µ + 1)x

j−1

)

4.2 Mechanistic Foundations of

FCGWO

The FCGWO builds upon the traditional GWO by re-

placing the random number generation process with

a sequence derived from fractional chaotic maps. In

FCGWO, the chaotic sequence is used to update the

position and velocity of the search agents (i.e., the

grey wolves) in the search space. The following out-

lines the key steps of the FCGWO algorithm:

1. Initialize the grey wolf population, along with

their positions and velocities.

2. Evaluate the ﬁtness of each grey wolf.

3. Calculate the social ranks (i.e., alpha, beta, and

delta wolves) based on the ﬁtness values.

4. Update the positions and velocities of the grey

wolves using the standard update rules (i.e., Equa-

tions (1) and (2)). However, the calculation of the

coefﬁcients

⃗

A and

⃗

C are updated using Fractional

Chaotic maps instead of random values following

the standard behavior. Then, the coefﬁcients

⃗

and

⃗

C are now computed as:

⃗

A = 2 ×⃗a ×

⃗

ψ(t) −⃗a (5)

⃗

C = 2 ×

⃗

ψ(t) (6)

5. Repeat steps 2-4 until a termination criterion is

met (e.g., maximum number of iterations, sufﬁ-

cient solution quality).

The introduction of the fractional chaotic sequence

ψ(t) in the FCGWO update rules fosters exploration

and diversiﬁcation, enabling the algorithm to avoid

local optima and efﬁciently search complex problem

landscapes. The following sections will delve deeper

into the potential applications and performance eval-

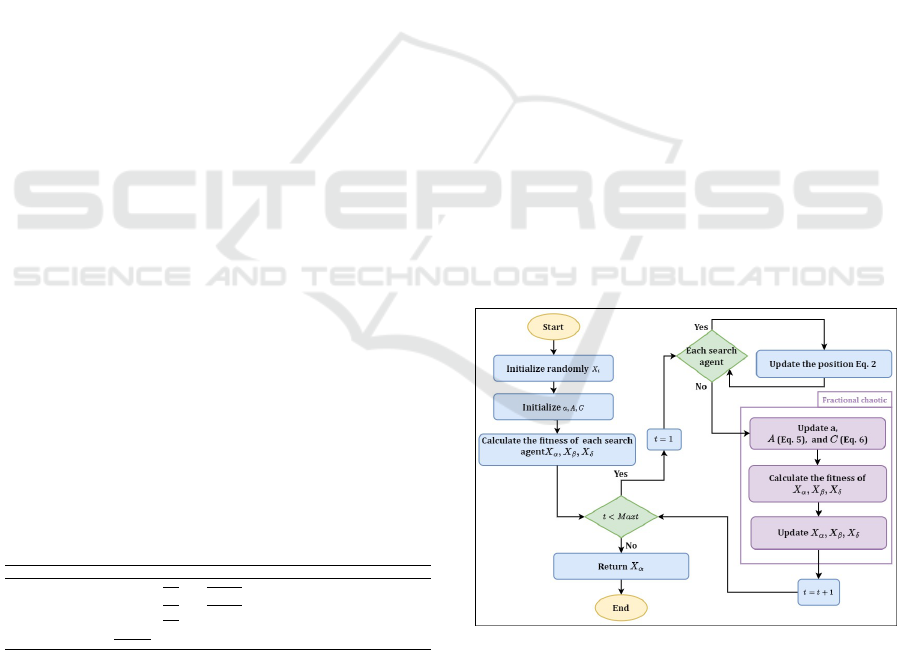
uation of the FCGWO algorithm. Figure 2 depicts the

ﬂowchart of the proposed FC-GWO algorithm.

Figure 2: Flowchart of FCGWO Algorithm.

5 LR-FCGWO FOR SOFTWARE

DEFECTS PREDICTION

The integration of LR with the FCGWO offers a

groundbreaking approach to SDP. LR, a standard

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

636

method for binary classiﬁcation, is especially use-

ful in SDP for its simplicity and interpretability. It

calculates the probability of a software module be-

ing defect-prone, a crucial aspect of software qual-

ity assurance. However, LR faces challenges such as

overﬁtting and inefﬁciency in high-dimensional data

spaces.

The FCGWO, inspired by the social and hunt-

ing behaviours of grey wolves and enhanced with

the dynamic capabilities of Fractional Chaotic maps,

is employed to address these limitations. This ad-

vanced metaheuristic algorithm optimizes LR param-

eters, aiding in tackling complex, high-dimensional

datasets prevalent in SDP. Traditional parameter tun-

ing methods often must catch up in such scenarios,

leading to overﬁtting or inadequate feature selection.

In contrast, FCGWO’s adaptive nature allows for a

more reﬁned and practical approach.

An added beneﬁt of FCGWO is incorporating

Fractional Chaotic maps, which boosts the algo-

rithm’s ability to escape local optima. This feature

is particularly valuable in handling the non-linear re-

lationships characteristic of SDP data, which standard

LR models may not effectively capture.

5.1 Objective Function

As previously mentioned, we employ the FCGWO al-

gorithm as a training mechanism for the logistic re-

gression model. Speciﬁcally, each potential solution,

comprising a set of weights and biases produced by

FCGWO, is evaluated using the LR model. The per-

formance of each solution ( f

) is then quantiﬁed using

the discrepancy (E

) between the predicted (p) and ac-

tual (y) outputs, as depicted in the equations below:

1 + E

(7)

∑

− y

)

(8)

where n is the number of rows used in the training set.

5.2 Data Preprocessing

For our work, we opted for the Min-Max method (Is-

lam et al., 2022), which simpliﬁes value comparisons.

Following normalization, we applied a data transfor-

mation method, which is an essential part of the ini-

tial data preparation before statistical analysis. This

method also facilitates comparison and interpretation.

Moreover, true (yes) and false (no) values were trans-

formed into 1s and 0s, respectively. We also em-

ployed cross-validation, a data resampling technique,

to assess the generalization ability of predictive mod-

els and prevent overﬁtting (Berrar, 2019).

5.3 LR-FCGWO Steps

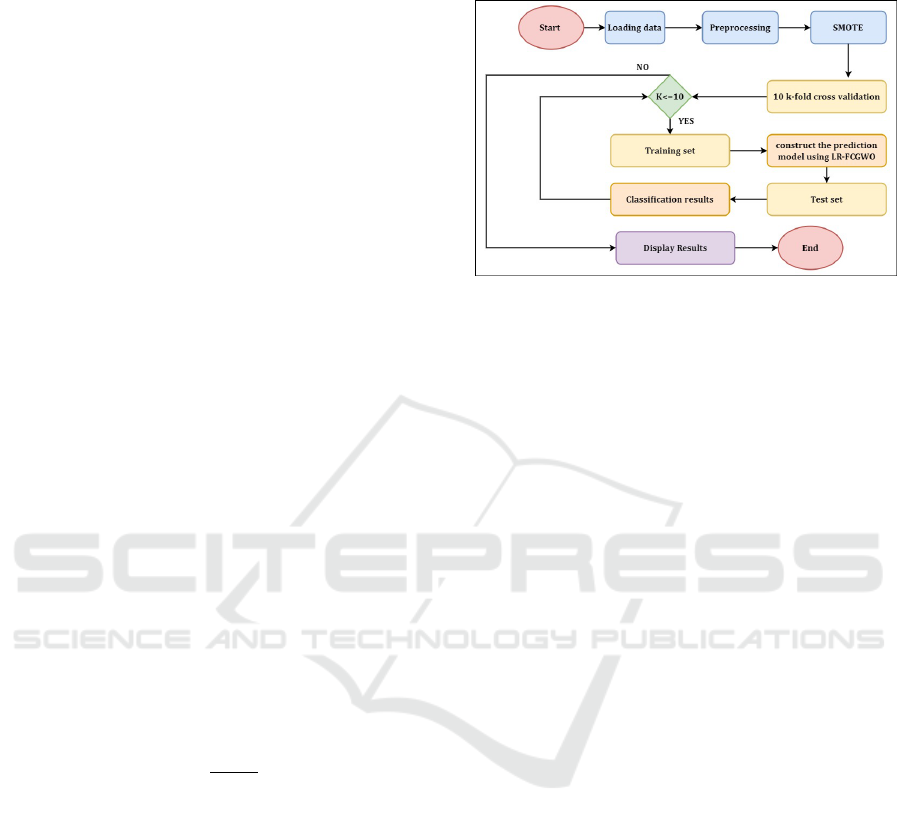
Figure 3: Flowchart of the LR-FCGWO Model for Software

Defect Prediction.

This section presents an overview of the LR-FCGWO

model’s workﬂow, illustrated in Figure 3. This work-

ﬂow is designed to systematically process software

metrics, apply optimization techniques, and utilize

predictive analytics to identify potential defects.

1. Loading Data. The process begins by importing

the relevant datasets to be used for software defect

prediction.

2. Preprocessing. Subsequently, data undergoes

preprocessing to conﬁrm it is ready for analysis.

This includes data cleaning, normalization, and

transformation procedures.

3. SMOTE. To counteract class imbalance within

the datasets, the Synthetic Minority Over-

sampling Technique (SMOTE) (Chawla et al.,

2002) is employed, which helps prevent model

bias towards the majority class.

4. 10 k-fold Cross Validation. Data is parti-

tioned into ten segments, and the model is cross-

validated to ensure robustness and to reduce the

risk of overﬁtting. This iterative cross-validation

is indicated by the decision diamond ’K¡=10’.

5. Training Set. The LR-FCGWO model is then

constructed using the training set obtained from

the cross-validation process.

6. Test Set. The model, now trained, is applied to

the test set to perform defect prediction.

7. Classiﬁcation Results. Outcomes of the classiﬁ-

cation are compiled to reﬂect the model’s perfor-

mance, as judged by metrics like accuracy, preci-

sion, and recall.

8. Display Results. The results from the classiﬁca-

tion process are then displayed.

Software Defect Prediction Using Integrated Logistic Regression and Fractional Chaotic Grey Wolf Optimizer

637

6 EXPERIMENTAL RESULTS

6.1 Datasets

In this study, ﬁve datasets from the PROMISE

REPOSITORY (Sayyad Shirabad and Menzies, 2005)

are selected, as shown in Table 2, varying in terms of

the number of lines and defect rates.

Table 2: Description of the Datasets.

Number of Yes No Number of Number of Missing

Attributes Instances Values

CM1 22 49 449 498 0

JM1 22 8779 2106 10885 0

KC1 22 326 1783 2109 0

KC2 22 105 415 522 0

PC1 22 1032 77 1109 0

6.2 Results and Discussions

In this section, all experiments were repeated 51 times

independently to obtain statistically signiﬁcant re-

sults, implemented using MATLAB R2020a.

The comparative analysis encompassed in the pre-

sented tables evaluates a range of machine learning

models: Logistic Regression (LR-standard), Random

Forest (Breiman, 2001), Gradient Boosting (Natekin

and Knoll, 2013), AdaBoost (Freund and Schapire,

1997), Support Vector Machine (SVM) (Kramer

and Kramer, 2013), K-Nearest Neighbors (K-NN)

(Kramer and Kramer, 2013), Decision Tree (Rokach

and Maimon, 2005), XGBoost (Chen and Guestrin,

2016), and Logistic Regression with CFGWO (LR-

CFGWO). These models are assessed across various

datasets, namely CM1, JM1, KC1, KC2, and PC1,

focusing on four key performance metrics: Accuracy,

Precision, Recall, and F1 Score.

In the CM1 dataset, LR-CFGWO stands out as the

most proﬁcient model, achieving the highest scores

across all metrics (Table 3). This model’s superior

performance is evident in its exceptional balance of

precision and recall, leading to a robust F1 Score.

Similarly, in the JM1 dataset, the Random Forest

model exhibits outstanding performance, marking the

highest scores in all evaluated metrics (Table 4). This

fact indicates its effectiveness in handling this dataset,

especially regarding accuracy and precision.

For the KC1 dataset, LR-CFGWO again shows

remarkable performance, topping the charts in all

metrics (Table 5). This consistency underscores the

model’s robustness and adaptability across different

datasets. In the analysis of the KC2 dataset, LR-

CFGWO and Random Forest models show compet-

itive performance. However, LR-CFGWO slightly

edges out with superior accuracy and precision, while

Table 3: Comparative Performance Analysis of Various Ma-

chine Learning Models on the CM1 Dataset.

Model Accuracy Precision Recall F1 Score

LR-standard 80.735 80.396 81.292 80.842

Random Forest 92.428 89.278 96.437 92.719

Gradient Boosting 90.646 86.573 96.214 91.139

AdaBoost 86.971 82.937 93.096 87.723

SVM 81.180 79.046 84.855 81.847

K-NN 83.519 75.904 98.218 85.631

Decision Tree 85.635 82.787 89.978 86.233

XGBoost 92.094 88.730 96.437 92.423

LR-CFGWO 92.984 89.549 97.327 93.276

Table 4: Comparative Performance Analysis of Various Ma-

chine Learning Models on the JM1 Dataset.

Model Accuracy Precision Recall F1 Score

LR-Standard 66.751 69.031 60.760 64.632

Random Forest 91.703 91.546 91.893 91.719

Gradient Boosting 81.957 84.140 78.759 81.361

AdaBoost 73.782 73.991 73.345 73.667

SVM 67.336 71.100 58.418 64.138

K-NN 81.826 75.132 95.145 83.962

Decision Tree 86.560 86.752 86.299 86.525

XGBoost 88.510 92.318 84.010 87.969

LR-CFGWO 87.875 92.210 82.740 87.219

Table 5: Comparative Performance Analysis of Various Ma-

chine Learning Models on the KC1 Dataset.

Model Accuracy Precision Recall F1 Score

LR-Standard 71.901 71.682 72.406 72.042

Random Forest 88.923 85.626 93.550 89.413

Gradient Boosting 84.773 83.120 87.269 85.144

AdaBoost 78.435 74.877 85.586 79.874

SVM 73.472 70.998 79.361 74.947

K-NN 81.716 75.167 94.728 83.821

Decision Tree 83.707 81.833 86.652 84.173

XGBoost 88.839 87.251 90.970 89.072

LR-CFGWO 89.484 88.344 90.970 89.638

Table 6: Comparative Performance Analysis of Various Ma-

chine Learning Models on the KC2 Dataset.

Model Accuracy Precision Recall F1 Score

LR-Standard 78.795 78.935 78.554 78.744

Random Forest 88.675 85.275 93.494 89.195

Gradient Boosting 87.711 85.812 90.361 88.028

AdaBoost 82.892 82.578 83.373 82.974

SVM 78.675 77.674 80.482 79.053

K-NN 81.084 76.113 90.602 82.728

Decision Tree 86.265 86.618 85.783 86.199

XGBoost 87.711 85.488 90.843 88.084

LR-CFGWO 88.916 87.298 91.084 89.151

Table 7: Comparative Performance Analysis of Various Ma-

chine Learning Models on the PC1 Dataset.

Model Accuracy Precision Recall F1 Score

LR-standard 80.814 79.336 83.333 81.285

Random Forest 95.736 94.444 97.190 95.798

Gradient Boosting 93.750 91.536 96.415 93.912

AdaBoost 89.874 87.240 93.411 90.220

SVM 83.285 77.769 93.217 84.795

K-NN 90.843 85.037 99.128 91.544

Decision Tree 91.812 90.065 93.992 91.987

XGBoost 95.785 94.787 96.899 95.831

LR-CFGWO 96.124 95.161 97.190 96.165

Random Forest excels in recall (Table 6), indicating

its strength in identifying relevant instances.

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

638

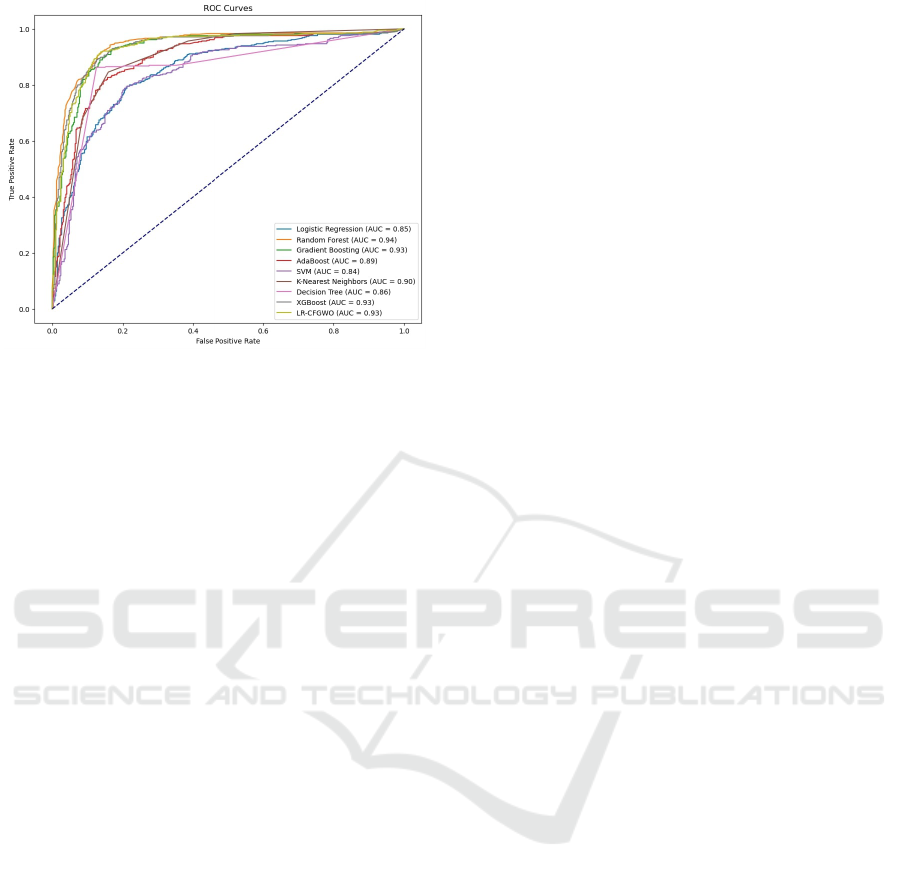
Figure 4: ROC Curve Analysis of Classiﬁer Performance

on KC2 Dataset.

In the PC1 dataset, LR-CFGWO again demon-

strates its dominance, leading in accuracy, precision,

and F1 Score (Table 7). The model’s consistent per-

formance across different datasets highlights its effec-

tiveness and reliability in various contexts.

After that, we present the Receiver Operating

Characteristic (ROC) curves for different classiﬁers

applied to KC2 dataset. ROC curves are a graphical

representation that illustrate the diagnostic ability of

binary classiﬁers as their discrimination threshold is

varied. The area under the ROC curve (AUC) pro-

vides a single measure of overall performance of a

classiﬁer. The closer the ROC curve is to the top-left

corner, the higher the overall accuracy of the test.

In Figure 4, the ROC curve for the KC2 dataset in-

dicates that the LR-FCGWO classiﬁer achieves a re-

markable AUC of 0.99, paralleling the excellent per-

formance of the Gradient Boosting classiﬁer. The

high AUC value underscores the LR-FCGWO clas-

siﬁer’s exceptional proﬁciency in discriminating be-

tween the classes.

Overall, the analysis reveals that while different

models have their strengths in speciﬁc datasets, LR-

CFGWO consistently emerges as a top performer,

showcasing its versatility and effectiveness in various

predictive tasks.

7 CONCLUSIONS

The LR-FCGWO methodology introduces an innova-

tive approach to Software Defect Prediction (SDP),

combining the predictive capabilities of Logistic Re-

gression with the optimization strengths of the Frac-

tional Chaotic Grey Wolf Optimizer (FCGWO). This

method enhances defect prediction by optimizing

model parameters, effectively addressing overﬁtting

and the challenges posed by high-dimensional data.

It leads to an improved and more detailed predictive

model for detecting software defects.

The potential avenues for further research and

application of the LR-FCGWO model are manifold

and promising. One prospective area of exploration

is the continued reﬁnement and optimization of the

FCGWO algorithm itself. Enhancing algorithmic efﬁ-

ciency or adaptability could further elevate the perfor-

mance of LR-FCGWO, especially in scenarios char-

acterized by exceedingly large or complex datasets.

REFERENCES

Acito, F. (2023). Logistic regression. In Predictive Analyt-

ics with KNIME: Analytics for Citizen Data Scientists,

pages 125–167. Springer.

ATALI, G., PehlIvan,

I., G

urevin, B., and S¸ EKER, H.

(2021). Chaos in metaheuristic based artiﬁcial in-

telligence algorithms: a short review. Turkish Jour-

nal of Electrical Engineering and Computer Sciences,

29(3):1354–1367.

Balogun, A. O., Basri, S., Jadid, S. A., Mahamad, S., Al-

momani, M. A., Bajeh, A. O., and Alazzawi, A. K.

(2020). Search-based wrapper feature selection meth-

ods in software defect prediction: an empirical analy-

sis. In Intelligent Algorithms in Software Engineer-

ing: Proceedings of the 9th Computer Science On-

line Conference 2020, Volume 1 9, pages 492–503.

Springer.

Berrar, D. (2019). Cross-validation. Encyclopedia of bioin-

formatics and computational biology, 1:542–545.

Breiman, L. (2001). Random forests. Machine learning,

45:5–32.

Buchari, M., Mardiyanto, S., and Hendradjaya, B. (2018).

Implementation of chaotic gaussian particle swarm

optimization for optimize learning-to-rank software

defect prediction model construction. In Journal

of Physics: Conference Series, volume 978, page

012079. IOP Publishing.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: synthetic minority over-

sampling technique. Journal of artiﬁcial intelligence

research, 16:321–357.

Chen, T. and Guestrin, C. (2016). Xgboost: A scalable

tree boosting system. In Proceedings of the 22nd acm

sigkdd international conference on knowledge discov-

ery and data mining, pages 785–794.

Eberhart, R. and Kennedy, J. (1995). Particle swarm

optimization. In Proceedings of the IEEE inter-

national conference on neural networks, volume 4,

pages 1942–1948. Citeseer.

Elsabagh, M., Farhan, M., and Gafar, M. (2020). Cross-

projects software defect prediction using spotted

hyena optimizer algorithm. SN Applied Sciences, 2:1–

15.

Software Defect Prediction Using Integrated Logistic Regression and Fractional Chaotic Grey Wolf Optimizer

639

Freund, Y. and Schapire, R. E. (1997). A decision-theoretic

generalization of on-line learning and an application

to boosting. Journal of computer and system sciences,

55(1):119–139.

Goyal, S. and Bhatia, P. K. (2021). Software fault predic-

tion using lion optimization algorithm. International

Journal of Information Technology, 13:2185–2190.

Holland, J. H. (1992). Genetic algorithms. Scientiﬁc amer-

ican, 267(1):66–73.

Islam, M. J., Ahmad, S., Haque, F., Reaz, M. B. I., Bhuiyan,

M. A. S., and Islam, M. R. (2022). Application of

min-max normalization on subject-invariant emg pat-

tern recognition. IEEE Transactions on Instrumenta-

tion and Measurement, 71:1–12.

Jin, C. and Jin, S.-W. (2015). Prediction approach of soft-

ware fault-proneness based on hybrid artiﬁcial neu-

ral network and quantum particle swarm optimization.

Applied Soft Computing, 35:717–725.

Johnson, P., Vandewater, L., Wilson, W., Maruff, P., Savage,

G., Graham, P., Macaulay, L. S., Ellis, K. A., Szoeke,

C., Martins, R. N., et al. (2014). Genetic algorithm

with logistic regression for prediction of progression

to alzheimer’s disease. BMC bioinformatics, 15:1–14.

Kang, J., Kwon, S., Ryu, D., and Baik, J. (2021). Haspo:

Harmony search-based parameter optimization for

just-in-time software defect prediction in maritime

software. Applied Sciences, 11(5):2002.

Kramer, O. and Kramer, O. (2013). K-nearest neighbors.

Dimensionality reduction with unsupervised nearest

neighbors, pages 13–23.

Manita, G., Chhabra, A., and Korbaa, O. (2023). Efﬁcient

e-mail spam ﬁltering approach combining logistic re-

gression model and orthogonal atomic orbital search

algorithm. Applied Soft Computing, 144:110478.

Manita, G., Khanchel, R., and Limam, M. (2012). Consen-

sus functions for cluster ensembles. Applied Artiﬁcial

Intelligence, 26(6):598–614.

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey

wolf optimizer. Advances in engineering software,

69:46–61.

Natekin, A. and Knoll, A. (2013). Gradient boosting ma-

chines, a tutorial. Frontiers in neurorobotics, 7:21.

Niu, Y., Tian, Z., Zhang, M., Cai, X., and Li, J. (2018).

Adaptive two-svm multi-objective cuckoo search al-

gorithm for software defect prediction. Interna-

tional Journal of Computing Science and Mathemat-

ics, 9(6):547–554.

Panda, M. and Azar, A. T. (2021). Hybrid multi-objective

grey wolf search optimizer and machine learning ap-

proach for software bug prediction. In Handbook of

Research on Modeling, Analysis, and Control of Com-

plex Systems, pages 314–337. IGI Global.

Qasim, O. S. and Algamal, Z. Y. (2018). Feature selec-

tion using particle swarm optimization-based logistic

regression model. Chemometrics and Intelligent Lab-

oratory Systems, 182:41–46.

Raheem, M., Ameen, A., Ayinla, F., and Ayeyemi, B.

(2020). Software defect prediction using metaheuris-

tic algorithms and classiﬁcation techniques. Ilorin

Journal of Computer Science and Information Tech-

nology, 3(1):23–39.

Rokach, L. and Maimon, O. (2005). Decision trees. Data

mining and knowledge discovery handbook, pages

165–192.

Roman, A., Bro

zek, R., and Hryszko, J. (2023). Predic-

tive power of two data ﬂow metrics in software defect

prediction.

Sayyad Shirabad, J. and Menzies, T. (2005). The PROMISE

Repository of Software Engineering Databases.

School of Information Technology and Engineering,

University of Ottawa, Canada.

Talbi, E.-G. (2009). Metaheuristics: from design to imple-

mentation. John Wiley & Sons.

Wahono, R. S., Suryana, N., and Ahmad, S. (2014). Meta-

heuristic optimization based feature selection for soft-

ware defect prediction. J. Softw., 9(5):1324–1333.

Wu, G.-C. and Baleanu, D. (2014). Discrete fractional

logistic map and its chaos. Nonlinear Dynamics,

75(1):283–287.

Wu, G.-C., Baleanu, D., and Zeng, S.-D. (2014). Discrete

chaos in fractional sine and standard maps. Physics

Letters A, 378(5-6):484–487.

Zhu, K., Ying, S., Zhang, N., and Zhu, D. (2021). Soft-

ware defect prediction based on enhanced metaheuris-

tic feature selection optimization and a hybrid deep

neural network. Journal of Systems and Software,

180:111026.

Zivkovic, T., Nikolic, B., Simic, V., Pamucar, D., and Ba-

canin, N. (2023). Software defects prediction by meta-

heuristics tuned extreme gradient boosting and analy-

sis based on shapley additive explanations. Applied

Soft Computing, 146:110659.

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

640