OER-Enabled Pedagogy with Multipurpose Digital

LMS-Quiz-Activities for Mathematics

Ana Donevska-Todorova

HTW Berlin, University of Applied Sciences, Treskowallee 8, 10318 Berlin, Germany

Keywords: Instructional Design, Educational Content Creation, next Generation Teaching and Learning Environments,

Feedback and Learning Support, Self-Regulated Learning, Synchronous and Asynchronous Learning,

Mathematics, Abstract Algebra, Linear Algebra, Task and Item Generation, Quiz, Learning Management

Systems (LMS), Dynamic Geometry Software (DGS), OER, OEP, OER-Enabled Pedagogy.

Abstract: On the boundaries between manual, adaptive and intelligent generation of e-quiz-tasks, this paper tackles their

didactical potentials and encounters for open teaching and learning of undergraduate mathematics. The most

flexible and personalized domain-specific learning content offering instantaneous assistive feedback is

desirable, yet not easy to be provided with or without the use of Artificial Intelligence (AI). Today’s “learners

on the go” seek fast and granulated learning content. However, overproduction may lead to a quantity of drill-

and-practice exercises that may be beneficial for procedural fluency, yet not enough to secure conceptual

understanding in mathematics and the development of 21

century skills. Therefore, based on four

theoretically defined criteria for OER-Enabled Pedagogy according to Wiley & Hilton Iii (2018), this paper

suggests small scale open resources combining Learning Management Systems (LMS) and Dynamic

Geometry Software (DGS). Their (1) added value is seen in the multi purposes of LMS-Moodle-Quiz-

Activities going beyond the commonly-accepted summative assessment: (i) self-regulated learning through

instantaneous feedback, (ii) collaboration, (iii) creativity, and (iv) procedural and conceptual understanding

in mathematics. The possible (2) application, revision, remix, or re-creation of the OER is discussed through

illustrative examples in Abstract and Linear Algebra. The paper finalizes with outlying the (3) share-ability

of the resources publicly, and their (4) open-licencing.

1 INTRODUCTION

The phrase “human-computer interaction” which

refers mainly to instructors as creators of learning

materials with the aid of technology and students as

consumers of those productions, might sound

somewhat outdated. The reality moves slowly, but

surely towards a modern catchy name “human-AI

tandem”, unfolding the distribution of equivalent

engagement of all parties: instructors, learners and

technologies in instruction design and its

consumption. If the technologies have become

sophisticated enough to be able to ‘feed’ themselves

with existing content and generate new, then it is

instructors’ responsibility to check their quality,

promote critical thinking and provide a learning

atmosphere for creative externalizations of thoughts

and emotions. Yet, until technologies reach that level

of intelligence, today’s modest digital systems may

undertake duties such as providing immediate

personal feedback to learners and, with that,

significantly unload the timely capacities of

instructors. Creation of comprehensive, modular

courses that accustom them to different learners’

individual wants, styles, learning rhythm, and

performance seem possible with the use of adaptive

elements in Learning Management Systems (LMS).

Although literature for Automatic Question

Generation (AQG) was considered (e.g. Le, Kojiri,

and Pinkwart, 2014) the aim of this work is not to

discuss a machine-generation of questions. It is rather

the consideration of didactical aspects that enable

educators to re-use or remix existing quiz-tasks or

create their own tasks and share them with others.

Therefore, the paper considers theoretically grounded

Open Educational Resources (OER) objectives and

areas of actions (UNESCO, 2019) having in mind the

5R (reuse, redistribute, revise, remix and retain,

according to Wiley, 2013). It also deliberates

challenges when creating and applying OER,

454

Donevska-Todorova, A.

OER-Enabled Pedagogy with Multipurpose Digital LMS-Quiz-Activities for Mathematics.

DOI: 10.5220/0012689700003693

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Computer Supported Education (CSEDU 2024) - Volume 1, pages 454-461

ISBN: 978-989-758-697-2; ISSN: 2184-5026

especially when learners face difficulties in self-

regulation and adaptation to OEP (Open Educational

Practices)-structured courses (Huang, et al., 2020).

The paper continues with criteria that enable OER-

Pedagogy for self-regulation, creativity, collaboration

and gaining specific competences in mathematics.

2 OER-ENABLED PEDAGOGY

Initiatives about open, flexible, and distance learning

(OFDL) originate in relation to the ideas about open

universities at the middle of the 20th century, but

have significantly changed since the COVID-19

pandemic (Naidu, 2023). According to Wiley &

Hilton Iii (2018), OER-Enabled Pedagogy can be

determined by four criteria: (1) added value of the

resources beyond its value for the author, (2) possible

application, revision, remix, or re-creation of the

resources, (3) share-ability of the resources publicly,

(4) open-licencing for the resources (Wiley & Hilton

Iii, 2018, p. 137).

The added value of the developed OER on small

scale (Weller, 2010) in this work that goes beyond the

value of its author (the first author of this text) is seen

as the following.

LMS-Quiz-Activities for developing 21

century

skills and learning purposes:

i. Self-regulated learning through automated

feedback

ii. Collaboration

iii. Creativity

iv. Procedural and Conceptual Understanding

in Mathematics

The paper begins with explaining each of these

values meeting the first criterion for OER-Enabled

Pedagogy (Wiley & Hilton Iii, 2018). It then

continues with discussions about each of the other

three criteria for OER-Enabled Pedagogy (Wiley &

Hilton Iii, 2018).

3 ADDED VALUE.

MULTIPURPOSE OF

LMS-QUIZ-ACTIVITIES

More than three decades ago, Hativa (1988) pointed

out that computer-based drill-and-practice in

Arithmetic may widen the gap between high- and low-

achieving elementary school learners due to technical

errors. As technologies have evolved, the didactical

benefits of CAI (Computer Assisted Instruction) have

also altered. Valuable contributions have raised novel

questions and brought different viewpoints into the

international debates. For example, expert guidance

and feedback are seen as key factors for the drive from

self-initiated practice to coached deliberate practice in

mathematics (Lehtinen, et al., 2017).

3.1 LMS-Quiz-Activities for

Self-Regulated Learning Through

Feedback

Current trends in higher education teaching depict a

movement from standardized assessment to automatic

formative assessment (AFA). For example, LMS-

Moodle quizzes are seen to be usable for formative

assessment in academic writing (Fernando, W., 2020).

The use of LMS-Moodle plugin STACK (System for

Teaching and Assessment using a Computer Algebra

Kernel) in university mathematics assessment was

already known much before the COVID pandemic

(e.g. Mäkelä, Ali-Löytty, Humaloja, Joutsenlahti,

Kauhanen, & Kaarakka, 2016; Sangwin, 2015). It

seems that potentials of (digital) tasks for mathematics

that were previously not well known were uncovered

during and after the pandemic (Engelbrecht, Borba, &

Kaiser, 2023). For example, production of numerous

mathematics exercises with specific step-by-step

feedback (Pulido-Rodríguez, López-Bautista, &

Gutiérrez-Rodríguez, 2021) received much attention,

not only in mathematics education, but also in science

education, programming and other non-mathematical

subjects.

Based on a repetitive randomized control

experiment, some authors “have not been able to

demonstrate a positive or negative effect of

personalized feedback on the grade performance of the

first year students” (Riezebos, N. Renting, R. van

Ooijen, A.J. van der Vaart, 2023, p. 50). These authors

have “made the choice to provide feedback based on

the achievement of module learning objectives, not on

the detailed level of the question itself” (Riezebos, N.

Renting, R. van Ooijen, A.J. van der Vaart, 2023, p.

50). Therefore, the tasks generated in this work provide

different types of feedback on task and item level,

besides on competences. This point is illustrated with

examples in Sub-section 4.1.1.

3.2 LMS-Quiz-Activities for

Collaboration

Besides through interactions with resources,

individual growth appears also through collaborative

actions with peers. To facilitate cooperative actions,

mathematical concepts that appear in the

formulations of the Quiz-tasks can be directly linked

OER-Enabled Pedagogy with Multipurpose Digital LMS-Quiz-Activities for Mathematics

455

with their definitions in the LMS-Moodle-Glossary-

Activity. Another possibility to meaningfully use the

Glossary is to provide appropriate feedback. So,

instead of stating the definition directly in the

Feedback option, the Feedback is formulated first as

a question and then linked to an appropriate concept

definition in the Glossary. The terms in the Glossary

can be offered by the instructor or suggested as a

collaborative activity. That is to say, learners have an

opportunity to enter new concept definitions in the

Glossary and collaboratively upgrade their

knowledge and support peers. Further explanations of

how such a combination of tasks, and Feedback

Options in Moodle Quiz activities and the Glossary

may work follows through examples from Abstract

Algebra in Sub-section 4.1.1.

3.3 LMS-Quiz-Activities for Creativity

Many of the default LMS-Moodle tasks ask learners

to respond on quests by a single click with the mouse.

To prevent passive learning and increase interactivity,

a shift in the teaching-leaning perspective allowing

students a role as designers was proposed by Damnik,

Proske & Körndle (2017). The LMS-Moodle-

StudentQuiz-Activity allows such alteration of roles

and provides possibilities for learners to contribute

their own quizzes, tasks, tasks- or feedback-items in

the learning environment. This opportunity certainly

opens questions about the quality of the resources

(Trgalova, Donevska-Todorova, & Edson, 2023) that

may be peer-reviewed, (dis)approved or revised by

the instructor within the LMS-Moodle-Course. The

LMS-Moodle-Statistics for this StudentQuiz-Activity

provides personal information on the number of

contributed and approved questions, rating average,

number of given answers, percentage of corrected

answers and personal progress. Further, the

StudentQuiz-Activity affords community statistics

about the number of all created and approved

questions, community percentage of correct answers

and average community progress. As building a

LMS-Moodle-StudentQuiz may be overwhelming

during a semester course, both the personal and

community statistics may contribute to further

development of the quiz by other groups of learners

in other LMS-Moodle-Courses.

3.4 LMS-Quiz-Activities for

Procedural and Conceptual

Understanding in Mathematics

Active participation and interaction with dynamic

mathematical objects like graphs of functions or

geometric figures through connecting the LMS with

external learning environments such as the DGS

GeoGebra. By integrating GeoGebra files in LMS-

Moodle-tasks, quizzes gain didactical quality due to

possibilities for active engagement of learners. For

example, incorporated DGS files into LMS-Moodle-

tasks can enable transitions between different

registers like, algebraic, geometric or abstract-

structural registers of mathematical concepts in

Linear Algebra. Thus, rather than focusing on

knowledge acquisition, the OER embedding DGS

and LMS in this work aim at stimulating switches

between different modes of thinking about concepts

like Vector spaces and their properties. Such an

illustrative example is provided in subsection 4.1.3.

The next section elaborates the second criterion

for OER-Pedagogy (Wiley & Hilton Iii, 2018).

4 APPLICATION, REVISION,

REMIX, AND RECREATION OF

LMS-QUIZ-ACTIVITIES

The modules Abstract and Linear Algebra are

intensive on symbolic language use, formula-based

routines, implementation of formal definitions,

proofs of theorems and applications in real problems.

All these characteristics make the creation of a digital

domain-precise content for these modules not easy

work for instructors. Moreover, the desired digital

resources should foster development of the

previously mentioned future skills like (i) self-

regulation, (ii) collaboration, and (iii) creativity,

besides the (iv) mathematical competences such as

procedural and conceptual understanding in the

specific subject-area of Algebra in OEP. Therefore,

conceptualization of academic courses that

significantly include created digital curricular

resources seems to be of importance and the next

subsection outlines possibilities for their practical

implementation.

4.1 Application of

LMS-Quiz-Activities

This paper suggests small scale (Weller, 2010)

digitally-based learning materials that include LMS-

Moodle-Activities like series of quizzes. They are

based on Moodle-Question Banks that include non-

STACK Moodle-tasks, such as curriculum-based

Multiple True/False questions, MCQ, Drag-and-Drop

tasks, Matching questions, and Numerical tasks with

the necessary application of LaTeX for the

CSEDU 2024 - 16th International Conference on Computer Supported Education

456

mathematical language and syntax and the CAS

Maxima background. Further, for more complex

tasks that consist of more sub-tasks, interactive

Embedded answers (Cloze) Moodle-question type

were developed. Such advance is enabled through a

previously installed up-to-date Moodle Version 4.1

and appropriate plug-ins at the University of Applied

Sciences HTW Berlin. The created prototypical

LMS-Moodle-Course and the digital learning

resources were offered to instructors at two

departments at the university in the winter semester

2023/24.

The Moodle version used for the creation of the

LMS Quiz Activities and the Question banks is 4.1,

which has a user-friendly interface and provides

barrier free elements such as superior optical

appearance compared with the previous Moodle

versions. The new navigation without the cogwheels,

the fresh look in which hidden elements are not

framed gray, but marked more conspicuously,

providing increased contrasts and space contribute to

improved possibilities for inclusion of all learners.

The usage of the created Question banks and Quiz

Activities does not require previous experience with

HTML or XML or programming skills.

Figure 1 shows a Homepage of an exemplary

OER-Moodle-Course in a development phase of

selected themes in Set Theory, Logic, Number Theory,

Abstract Algebra and Linear Algebra in introductory

mathematics for bachelor study programs developing

at the University for Applied Sciences HTW Berlin.

Appropriate icons were selected and implemented to

enable easy navigation and create a user-friendly

interface for the course (Figure 1, left). For example,

an icon presenting the ordering aspect of natural

numbers or an icon with the number ten suggesting the

number system with base 10 (Figure 1, left) aims to

attract the learners’ attention.

The created Moodle activities are characterized

with a double randomization of the tasks within a quiz

and of the answer-choices within MCQs, Drag-and-

Drop or Matching tasks. That can be achieved by

activating the function shuffle both when creating the

quiz and each of the tasks. Each task has three

attributed tags that enable easier search of the

question bank: a mathematical concept, a question

type and language (English or German).

Differentiated approaches for learners in

heterogeneous groups or individual learners are

facilitated through multiple attempts carefully guided

by specific feedback items and hints in a Moodle-

Quiz-Activity and through and Moodle-Student-

Quiz-Activity (Figure 1, right).

4.1.1 LMS-Quiz-Activities for

Self-Regulated Learning Through

Feedback and Collaboration: An

Example for Abstract Algebra

Questions within the quizzes are created to behave

interactively permitting multiple tries within the quiz.

This is advantageous compared to the adaptive mode

or the adaptive without penalties mode because it

allows feedback in addition to the possibility for

multiple attempts. It is also more beneficial for

learning compared to the deferred feedback mode for

the reason that it displays the feedback messages

directly after each answer submission rather than all

of them once the whole quiz is completed. The

created quizzes permit unlimited number of attempts

enabling the option each attempt builds on the last.

This consents learners on the different attempt to

concentrate exclusively on those tasks that were

answered erroneously on the prior attempt and rework

the tasks in the same ordering, regardless of

randomisation settings.

A Moodle-Quiz-Multiple-True/False-Task is

posed about monoids and Abel semigroups (Figure

2). Students are asked to make decisions about the

algebraic structure of the set of Natural numbers and

the binary operations standard addition, i.e.

multiplication.

Figure 1: An exemplary OER-Moodle-Course for introductory university mathematics.

OER-Enabled Pedagogy with Multipurpose Digital LMS-Quiz-Activities for Mathematics

457

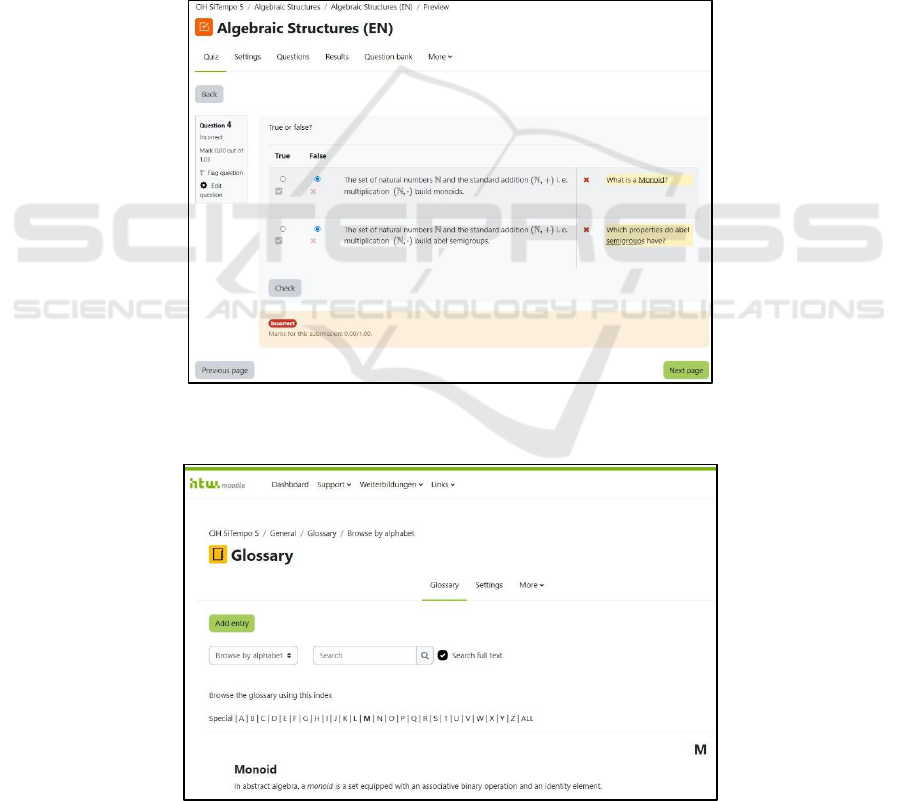
The Correctness of the Answer Feedback (CF)

appears below the task (the orange area on Figure 2).

It is presented with a red colour, because the entered

answer is incorrect (Figure 2). The subject-specific

Feedback of such an incorrect solution is presented in

the form of a question on each task item (on the right

side of Figure 2 with a yellow colour). The feedback

items refer to mathematical concepts that are

underlined and connected with their appropriate

definitions in the Moodle-Glossary-Activity (Figure

3). The underlying colouring, changing fonts into

bold or italic is a task-design-matter aiming to attract

the attention of the learner so that the term may be

clicked, and guidance is provided. The Glossary is

organized alphabetically and can be searched by

terms (Figure 3). Bearing in mind the suggested

definition, learners can resolve the given task in the

next attempt correctly. If so, they are shown the

Correctness of the Answer Feedback (CF) again. This

time the answer is “Correct” and the CF is presented

with a green instead of red colour together with the

scored points.

4.1.2 LMS-Quiz-Activities for Creativity

As previously discussed, LMS-Quiz-Activities may

offer a way to design and share personally created

tasks or items. A LMS-Moodle-StudentQuiz-Activity

called “Get Creative!” is suggested within the OER

LMS-Moodle-Course (Figure 1, right, above in

Section 4.1). It can be easily accessed and appears in

the second layer of the Moodle-Course-Tiles.

Figure 2: Subject-specific feedback to an incorrect answer of a Moodle-Quiz-Multiple True/False-Task appearing in a form

of a question (yellow area).

Figure 3: Collaboratively defining mathematical concepts in the Moodle-Course-Glossary, linking and using tasks or feedback

items.

CSEDU 2024 - 16th International Conference on Computer Supported Education

458

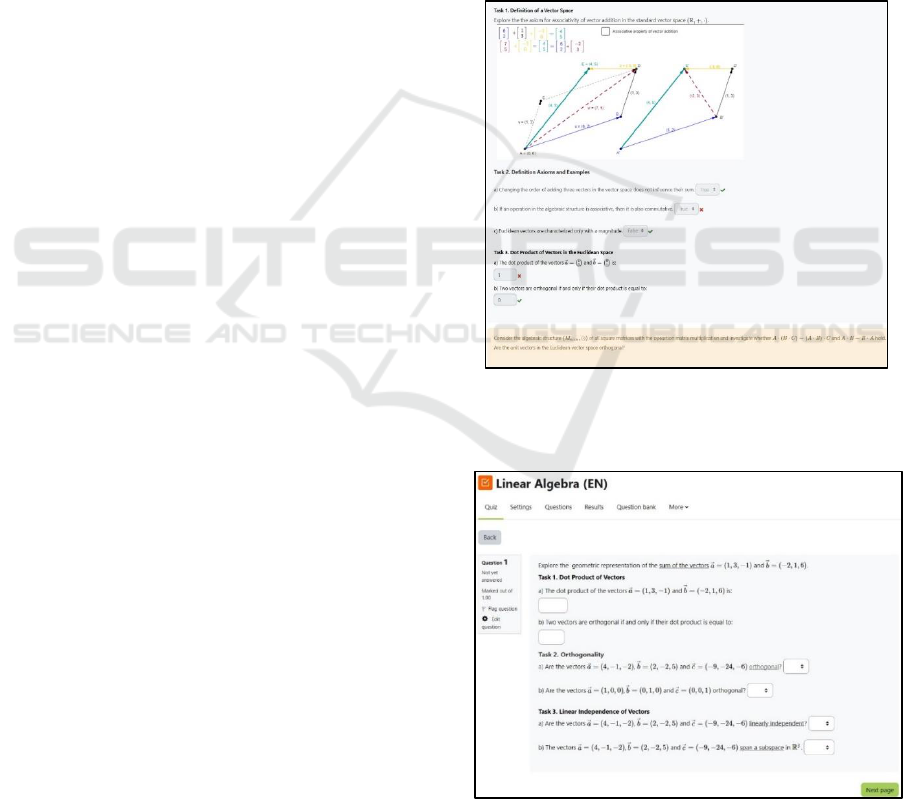
4.1.3 LMS-Quiz-Activities for Procedural

and Conceptual Understanding in

Mathematics

It is often the case that the formulation of a

mathematical task requires a content-related

visualisation, e.g. a geometric figure, a diagram, or a

graph of a function. Implementation of such images

is possible in a Cloze type of Moodle-tasks. For

example, a Moodle Embedded answers (Cloze) type

of task consisting of three sub-tasks is shown in

Figure 4. It contains three Matching questions and

two Numerical questions for fostering learners’

competences in Linear Algebra (Donevska-

Todorova, 2018) (Figure 4). The first sub-task is

about the definition of the Euclidean vector space and

the standard operation of vector addition and scalar

multiplication. After exploring the dynamic

visualization with algebraic and geometric interactive

elements in a GeoGebra file that is linked to the

Moodle-Cloze type of task, students are expected to

provide a correct answer on Task 2a) that changing

the order of any three vectors does not influence their

sum (Figure 4). However, a common mistake is

considering an operation to be commutative if it is

associative. Therefore, this is explicitly formulated as

a statement in sub-task 2b) (Figure 4) which is to be

confirmed as true if rejected as a false one. By

selecting “True”, which is an incorrect answer,

feedback (in orange colour in Figure 4) will appear

immediately after the answers are submitted. The

sub-task 3 is about the dot product of orthogonal

vectors.

A second Cloze type of Moodle-task, consisting

of three sub-tasks is presented in Figure 5. The first

sub-task extends the concept of dot product to

arbitrary vectors in the Euclidian 3D vector space.

The second sub-task is about orthogonality of specific

and arbitrary vectors. The third sub-task is related to

linear independence of vectors, base, span of a vector

space and subspace (Figure 5).

4.2 Revision, Remix and Recreation of

the Resources

Currently, tasks and quizzes in the LMS Moodle are

generated and edited through a web-based HTML

editor, exclusively possible via the internet.

Discontentment may appear due to the fact that all

information about an entire quiz cannot be visible as

a whole, but in a separate webpage for each task and

the dissatisfaction may grow when managing

graphics (Hendrickson & Guerquin-Kern, 2016).

Hendrickson & Guerquin-Kern (2016) suggest

automatic generation of different types of LMS-

Moodle-Questions including Cloze Questions, by

using special moodle packages via LaTeX. Other

authors propose developing Web applications for

easily creating quizzes involving Cloze format

questions in PHP where Moodle is also written such

as Ajax (Asynchronous JavaScript + XML) as a

graphical user interface (GUI) technique that easily

performs quiz editing (Yuuichi, et al., 2006). Bachiri

& Mouncif, 2023) offer an AI system in aid of

pedagogical engineering for knowledge assessment

on MOOC platforms: open EdX and Moodle. The

time-consuming task revision and re-creation by

typing LaTeX mathematical formulas in LMS can

become easier and faster with the aid of generative AI

Figure 4: LMS-Moodle-Cloze-Task about Vector Space

Definition with an integrated DGS File with algebraic,

geometric and axiomatic elements.

Figure 5: LMS-Moodle-Cloze-Task about Linear Algebra

Concepts: Dot Product of Vectors, Orthogonality and

Linear Independence of Vectors.

OER-Enabled Pedagogy with Multipurpose Digital LMS-Quiz-Activities for Mathematics

459

converting scans of already written formulas into the

LaTeX syntax. Such transformation that emerging

technologies propose may empower instructors and

contribute to increasing the sustainability of OER.

Finally, modernizing mathematics curricula that will

allow sought flexibility and personal adjustments

according to context and settings through cooperative

development by different stakeholders may

contribute to easier scale and sustainability.

5 SHARE-ABILITY OF THE

RESOURCES PUBLICLY

The third criterion for OER-Enabled Pedagogy

according to Wiley & Hilton Iii (2018), as given in

Section 2, is the possibility for sharing resources with

others. The aim of the share-ability is that the created

resources become reusable in new contexts and

settings or become a source of renewal and upgrade.

The suggested curricular OER in this paper are

available in English and German, which can facilitate

easier dissemination. They are visible via the link:

https://moodle.htw-berlin.de/course/view.php?id=

38124 using the password: MatheWin24. Exporting

and importing them into other Moodle courses is

possible by the use of the Moodle-XML-format or in

another non-Moodle application in the XHTML-

format. Both file formats allow exporting and

importing of all questions in the question bank and its

categories.

6 OPEN-LICENCING

A come back to the criteria for OER-Enabled

Pedagogy (Wiley & Hilton Iii, 2018), leads to the last,

but not least one, licencing.

Instructors and learners who “donate” their

artefacts to OER are considered to be authors and

products that they have created under a specific CC

License. To secure the quality of open resources, a

Creative-Commons (CC) Licence can be used.

7 CONCLUSIONS

Based on four theoretically defined criteria for OER-

Enabled Pedagogy (Wiley & Hilton Iii, 2018), this

paper considers multiple purposes for developing,

implementing and sharing LMS-Quiz-Activities

beyond summative assessment. Although limitations

refer to the current regulated accessibility for

university-external users of the resources, four

prospects can be outlined. Firstly, (1) an added value

of the proposed OER is seen in their potential to foster

improvement of skills such as self-regulated

learning, collaboration, and creativity, in addition to

subject-related competences in mathematics

(discussed in Section 3). Secondly, a possible (2)

implementation of the created OER in the light of

these added values is envisioned and exemplified

through a Moodle-Quiz-Multiple-True/False-Task

about Algebraic Structures and two Moodle-Quiz-

Embedded-Answers (Cloze)-Tasks about Linear

Algebra (Sub-section 4.1). Revision, recreation and

small scale of the OER, is possible by the use of the

widely spread compatible tools (Edit and Duplicate

options in LMS-Moodle) and, moreover with the aid

of advanced software and techniques, as described in

Sub-section 4.2. Thirdly, the created (3) OER are

shared and made publicly available through a direct

link to the LMS-Moodle-Course (Section 5). Finally,

the offered OER can be licensed (Section 6) which

opens gates for further work.

ACKNOWLEDGMENTS

The work presented in this paper is part of the project

Curriculum Innovation Hub at the HTW Berlin -

University of Applied Sciences and financed by the

“Stiftung Innovation in der Hochschullehre”.

The Author thanks all anonymous reviewers for

their valuable comments contributing to the

improvement of the article.

REFERENCES

Bachiri, Y. A., & Mouncif, H. (2023). Artificial intelligence

system in aid of pedagogical engineering for knowledge

assessment on MOOC platforms: open EdX and

moodle. International Journal of Emerging

Technologies in Learning (Online), 18(5), pp. 144-160.

Damnik, G., Proske, A. & Körndle, H. (2017). Designing a

constructive learning activity with interactive elements:

the effects of perspective-shifting and the quality of

source material, Interactive Learning Environments,

25:5, 634-649, DOI: 10.1080/10494820.2016.1172239.

Donevska-Todorova, A. (2018). Fostering students’

competencies in linear algebra with digital resources.

Challenges and strategies in teaching linear algebra,

261-276.

Engelbrecht, J., Borba, M. C., & Kaiser, G. (2023). Will we

ever teach mathematics again in the way we used to

CSEDU 2024 - 16th International Conference on Computer Supported Education

460

before the pandemic?. ZDM–Mathematics Education,

55(1), 1-16.

Fernando, W. (2020). Moodle quizzes and their usability

for formative assessment of academic writing.

Assessing Writing, 46, 100485.

https://doi.org/10.1016/j.asw.2020.100485.

Hativa, N. (1988). Computer-Based Drill and Practice in

Arithmetic: Widening the Gap between High- and Low-

Achieving Students. American Educational Research

Journal, 25(3), 366–397.

https://doi.org/10.2307/1163169

Hendrickson, A., & Guerquin-Kern, M. (2016). The

moodle package: generating Moodle quizzes via

LaTeX. Recuperado de https://www. ctan.

org/pkg/moodle Hendrickson, A, 654-667.

Huang, R., Liu, D., Tlili, A., Knyazeva, S., Chang, T. W.,

Zhang, X., Burgos, D., Jemni, M., Zhang, M., Zhuang,

R., & Holotescu, C. (2020). Guidance on Open

Educational Practices during School Closures: Utilizing

OER under COVID-19 Pandemic in line with

UNESCO OER Recommendation. Beijing: Smart

Learning Institute of Beijing Normal University.

Le, N.-T., Kojiri, T. and Pinkwart, N. (2014). Automatic

question generation for educational applications–the

state of art, in Advanced computational methods for

knowledge engineering. Springer, pp. 325–338.

https://doi.org/10.1007/978-3-319-06569-4_24

Lehtinen, E., Hannula-Sormunen, M., McMullen, J. et al.

(2017). Cultivating mathematical skills: from drill-and-

practice to deliberate practice. ZDM Mathematics

Education 49, 625–636.

https://doi.org/10.1007/s11858-017-0856-6

Mäkelä, A. M., Ali-Löytty, S., Humaloja, J. P., Joutsenlahti,

J., Kauhanen, J., & Kaarakka, T. (2016). STACK

assignments in university mathematics education. In

ANNUAL CONFERENCE OF THE EUROPEAN

SOCIETY FOR ENGINEERING EDUCATION.

European Society for Engineering Education SEFI.

Naidu, S. (2023). From open access to open science—Open

education in transition, Distance Education, 44:4, 599-

603, DOI: 10.1080/01587919.2023.2278218

Trgalova, J., Donevska-Todorova, A., & Edson, A. J.

(2023). Evaluation of Digital Resources: The “How”

and “What for”. In B. Pepin, G. Gueudet & J. Choppin

(Eds.), Handbook of Digital Resources in Mathematics

Education (pp. 1-28). Cham, Suisse: Springer.

doi:https://doi.org/10.1007/978-3-030-95060-6_45-1

Pulido-Rodríguez, G., López-Bautista, R., & Gutiérrez-

Rodríguez, I. (2021). Python, Stack and Moodle:

Programming and production of thousands of math

exam exercises with specific step-by-step feedback. In

ICERI2021 Proceedings (pp. 3454-3462). IATED.

Riezebos, J., Renting, N., van Ooijen, R., & van der Vaart,

A. J. (2023). Adverse effects of personalized automated

feedback. In 9th International Conference on Higher

Education Advances, HEAd 2023 (pp. 45-50).

Universidad Politecnica de Valencia.

http://dx.doi.org/10.4995/HEAd23.2023.16195

Sangwin, C. (2015, July). Computer aided assessment of

mathematics using STACK. In Selected regular

lectures from the 12th international congress on

mathematical education (pp. 695-713). Cham: Springer

International Publishing.

UNESCO (2019). Recommendations on Open Educational

Resources (OER). Retrieved [on 18.03.2024] from:

https://unesdoc.unesco.org/ark:/48223/pf0000373755/

PDF/373755eng.pdf.multi.page=3

Wiley, D. (2013). What is open pedagogy? Retrieved from

https://opencontent.org/blog/ archives/2975.

Wiley, D., & Hilton Iii, J. L. (2018). Defining OER-enabled

pedagogy. The International Review of Research in

Open and Distributed Learning, 19(4).

Weller, Martin (2010). Big and Little OER. In Open Ed

2010 Proceedings. Barcelona: UOC, OU, BYU.

[Accessed: 15/01/2024].

https://openaccess.uoc.edu/handle/10609/4851

Yuuichi, S., Toshihiro, K., Seisuke, Y., & Hiroshi, N.

(2006, July). Web-based rapid authoring tool for LMS

quiz creation. In 2006 7th International Conference on

Information Technology Based Higher Education and

Training (pp. 617-620). IEEE.

OER-Enabled Pedagogy with Multipurpose Digital LMS-Quiz-Activities for Mathematics

461