Improving Lane Level Dynamics for EV Traversal: A Reinforcement

Learning Approach

Akanksha Tyagi, Meghna Lowalekar and Praveen Paruchuri

International Institute of Information Technology Hyderabad (IIIT-H), Hyderabad, India

Keywords:

Reinforcement Learning, Emergency Vehicles, Lane Level Dynamics.

Abstract:

Emergency vehicles (EVs) perform a critical task of attending medical emergencies and delay in their opera-

tions can result in loss of lives to long term or permanent health implications. Therefore, it is very important

to design strategies that can reduce the delay of EVs caused by slow moving trafﬁc. Most of the existing work

on this topic focuses on assignment and dispatch of EVs from different base stations to hospitals or ﬁnding the

appropriate routes from dispatch location to hospital. However, these works ignore the effect of lane changes

when EV is travelling on a stretch of a road. In this work, we focus on lane level dynamics for EV traversal

and showcase that a pro-active picking of lanes can result in signiﬁcant reductions in traversal time. In partic-

ular, we design a Reinforcement Learning (RL) model to compute the most optimal lane for an EV to travel

at each timestep. We propose RLLS (Reinforcement Learning based Lane Search) algorithm for a general

purposes EV traversal problem and perform a series of experiments using the well-known trafﬁc simulator

SUMO. Our experimentation demonstrates that our model outperforms the default SUMO algorithm and is

also signiﬁcantly better than the existing state-of-the-art heuristic approach BLS (Best Lane Search) strategy

in normal trafﬁc conditions. We also simulate worst case scenarios by introducing slowed down vehicles at

regular time intervals into the trafﬁc and observe that our model generalizes well to different trafﬁc scenarios.

1 INTRODUCTION

Emergency vehicles (EV) are a class of vehicles

which include ambulances, ﬁre trucks, police cars etc.

They are dispatched from their base stations to disas-

ter site to respond to medical emergency, ﬁre disaster

among others. Any small delay in their operation can

result in loss of life or long term damage or implica-

tions to health. Hence, even a small improvement in

their traversal time can have signiﬁcant impact. In the

case of any medical emergency or disaster, a call is

sent to a helpline such as 911 and upon receiving the

call, the helpline connects with the appropriate base

station to dispatch the EV. There are multiple criti-

cal decisions here which can have an impact on the

overall response time. The ﬁrst decision is, which

base station should dispatch the EV vehicle (Ghosh

and Varakantham, 2018; Haghani et al., 2003; Joe

et al., 2022). The second decision is, what is the route

that the EV will take to travel from the base station

to emergency site and then from the emergency site

to hospital(s) (Giri et al., 2022; Su et al., 2022). The

third decision which is mostly overlooked is, when

an EV enters a stretch of road in its route, which

lane should the EV travel on (Agarwal and Paruchuri,

2016; Cao and Zhao, 2022). As demonstrated in ear-

lier works (Agarwal and Paruchuri, 2016), the lane

level dynamics can also play a crucial role in reducing

the EV traversal time and hence the overall response

time resulting in saving more lives and reduction of

long term health implications. The existing work re-

lies on heuristic approaches for lane level dynamics

which can be myopic in nature and hence cannot cap-

ture the long term effect of decisions. Therefore, in

this work we focus on improving the lane level dy-

namics for EV traversal using a reinforcement learn-

ing approach.

Our ﬁrst contribution is to model the problem of

lane level dynamics of EV using Markov Decision

Process (MDP) (Puterman, 2014). The modelling of

the problem as MDP allows us to use reinforcement

learning algorithm to learn the best way to choose the

appropriate lane for the EV to travel at each timestep.

We propose RLLS - a Reinforcement Learning based

Lane Search which uses the Advantage Actor-Critic

method (Mnih et al., 2016) to learn the MDP pol-

icy. We compare RLLS with the baseline approaches

using the SUMO (Simulation of Urban MObility)

134

Tyagi, A., Lowalekar, M. and Paruchuri, P.

Improving Lane Level Dynamics for EV Traversal: A Reinforcement Learning Approach.

DOI: 10.5220/0012637200003702

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2024), pages 134-143

ISBN: 978-989-758-703-0; ISSN: 2184-495X

(Lopez et al., 2018) trafﬁc simulator, which simulates

real trafﬁc scenarios. SUMO offers a designated ve-

hicle class known as emergency, facilitating the sim-

ulation of emergency vehicles and their unique priv-

ileges. Vehicles classiﬁed as emergency vehicles are

automatically assigned default shapes and sizes suit-

able for rescue operations. They possess special pre-

vileges, such as the ability to overtake on the right side

in all trafﬁc scenarios. Additionally, these vehicles are

permitted to traverse lanes speciﬁcally designated for

”emergency” use, which may restrict normal passen-

ger trafﬁc. This functionality within SUMO enables

an accurate modeling of emergency vehicle behaviors

and trafﬁc dynamics. We showcase that RLLS can re-

duce the EV travel time signiﬁcantly as compared to

this default (SUMO emergency) baseline.

Our second contribution is the introduction of ex-

perimental settings which can help with evaluating the

worst case performance of algorithms. To evaluate

the worst case performance of algorithms, we intro-

duce slowing down vehicles at regular time intervals

into the trafﬁc. These slowing down vehicles block

the trafﬁc and introduce more congestion in the trafﬁc

network. This simulation setting helps with evalua-

tion of the robustness of algorithms. Using a wide

range of experiments, we showcase that our RLLS

model trained using normal trafﬁc scenarios can gen-

eralize well to these worst case settings and we do not

need to train separate models for the different trafﬁc

scenarios.

In addition, we also evaluate the performance of

our approaches on real word dataset by using real

time speed data from New York City trafﬁc (NYD,

2022) to calibrate trafﬁc in a simulation. In this set-

ting as well, RLLS model outperforms the existing

approaches. In all the settings, for purposes of realis-

tic modeling, we also allow the EV to communicate

with other vehicles within a communication distance

. This is equivalent to communication done by an

EV using a siren in real world scenarios.

2 RELATED WORK

The ﬁrst thread of research focuses on ﬁnding strate-

gies for the assignment of EV to incoming requests

(emergency calls) (Ghosh and Varakantham, 2018;

Haghani et al., 2003; Joe et al., 2022; Schmid, 2012).

(Schmid, 2012), formulates the problem of ﬁnding

the optimal dispatch strategy as an approximate dy-

namic programming problem and uses value function

approximation strategies to ﬁnd the assignment of EV

to emergency calls at each timestep. (Ghosh and

Varakantham, 2018) formulate the problem as an in-

teger optimization problem and use Benders decom-

position to ﬁnd a solution to the integer optimization

problem.

The second thread of research focuses on ﬁnding

the best route for EV to travel from base station to the

disaster location and from disaster location to hospi-

tal(s) (Giri et al., 2022; Su et al., 2022; Jotshi et al.,

2009). A sub-thread of this line of work, is the co-

ordination of trafﬁc signal control to mitigate trafﬁc

congestion and as a result to allow EV to reach the

destination quickly (Asaduzzaman and Vidyasankar,

2017; Chen et al., 2020; Chu et al., 2019; Van der Pol

and Oliehoek, 2016).

The last thread of research which is most rele-

vant to this paper is related to improving the lane

level dynamics of Emergency vehicles (Agarwal and

Paruchuri, 2016; Ismath et al., 2019; Cao and Zhao,

2022). In this thread of work, focus is on under-

standing and computing the value of each lane so to

pick the best feasible lane to optimize on the travel

time. (Zhang et al., 2022) focuses on safe lane-

changing trajectories for autonomous driving in ur-

ban environments to enhance the efﬁciency as well

as safety. (Maleki et al., 2023) studies a real-time

optimal cooperative lane change strategy leverag-

ing V2V communication, prioritizing safety and efﬁ-

ciency through constrained optimization. While these

approaches primarily address normal trafﬁc scenar-

ios using heuristic methods, our strategy formulates

the challenge of minimizing EV traversal time as an

MDP and employs RL techniques. Additionally, we

introduce scenarios with random slowing vehicles to

add complexity and enhance the realism of the simu-

lation. There are different assumptions and aspects of

the problem e.g., nature of communication, range of

communication, communication protocol to use, priv-

ileges of EV etc. that can affect the lane level decision

making process. Please note that while trafﬁc simu-

lators will need to handle vehicle routing which in-

volves changing of lanes, decisions to switch lanes are

myopic in nature in general even though route plan-

ning tends to get optimized in a global sense.

3 BACKGROUND

The handling of lane level dynamics in EV traversal

consists of picking the best lane for EV to travel while

traversing a multi lane stretch of road. Similar to ex-

isting work, we assume the presence of a V2V single

hop communication model where EV can obtain the

position and speed of a vehicle in any lane up to a

ﬁxed communication distance, c

via V2V commu-

nication. It can also send lane change requests to

Improving Lane Level Dynamics for EV Traversal: A Reinforcement Learning Approach

135

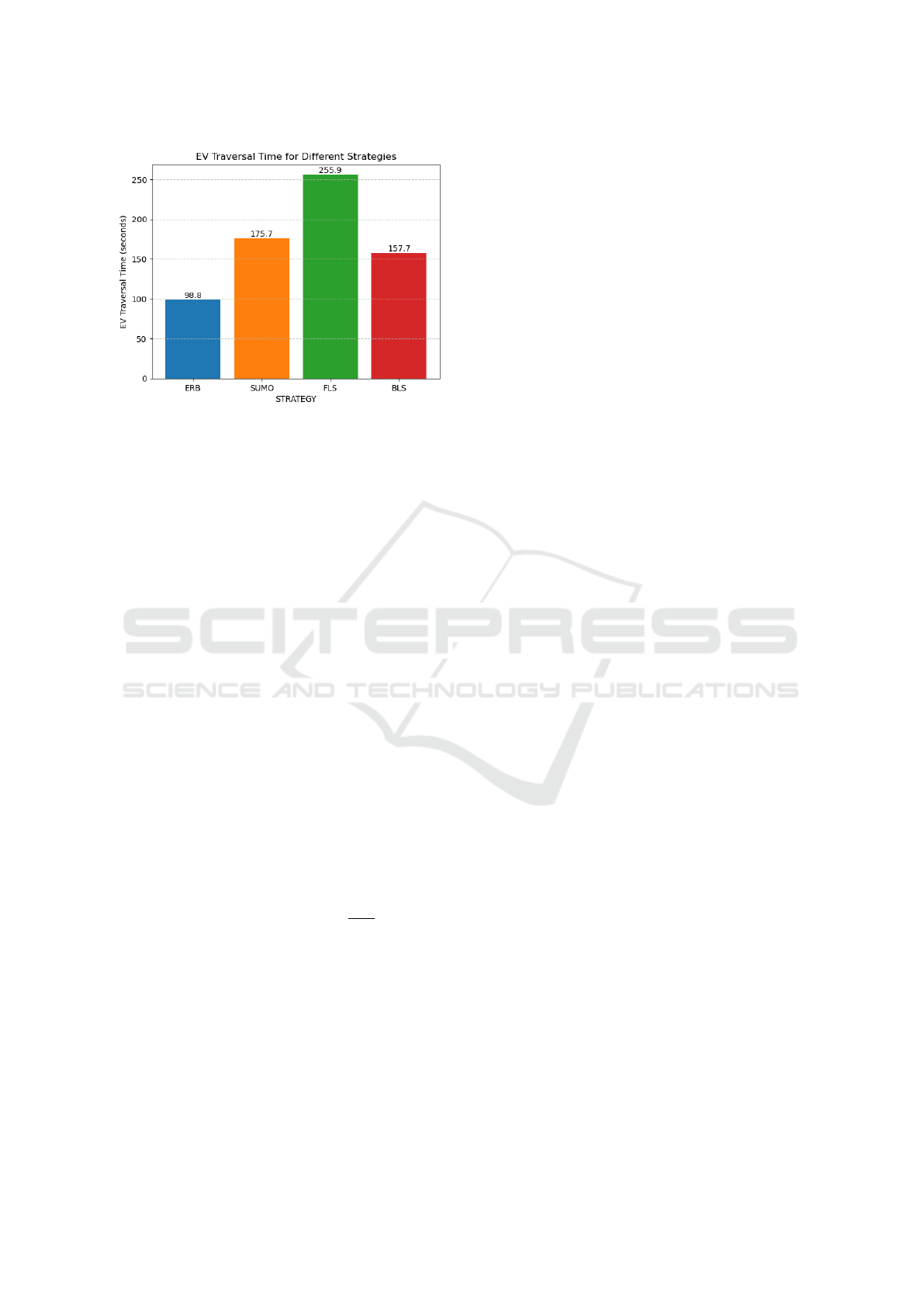
Figure 1: Comparison of EV Traversal Time for ERB,

SUMO, FLS and BLS Strategies.

the vehicles ahead of EV in its current lane within

this communication distance, c

, to clear the trafﬁc.

Upon receiving the request from EV, vehicles attempt

to change the lane and if there is no vehicle present in

the destination lane, the lane change action would be

successful.

(Agarwal and Paruchuri, 2016) introduced the fol-

lowing two strategies to ﬁnd the best lane for EV.

• FLS (Fixed Lane Strategy). In this strategy, EV

identiﬁes the lane, that is fastest on an average,

based on prior information and picks that lane as

the ﬁxed lane for its entire journey.

• BLS (Best Lane Strategy). In this strategy, at each

timestep, EV identiﬁes the best lane using the util-

ity values for each lane and switches to the best

identiﬁed lane. BLS computes utility of lane i us-

ing the following equation:

= w

∗ A

+ w

∗ B

+ w

∗ µ

where A

denotes the normalized speed of the

slowest vehicle on lane i, B

denotes the normal-

ized average speeds of the vehicles on the lane i

and µ

denotes the normalized free space on the

lane i. The normalized free space is an approx-

imation and is computed using

−c

, where n

is the maximum number of vehicles that can be

present on lane i within communication distance

and c

is the number of vehicles present on the

lane i within communication distance c

In their experiments, the paper (Agarwal and

Paruchuri, 2016) compares the above two strategies

against the following baseline strategies:

• SUMO. SUMO (Simulation of Urban MObil-

ity) (Lopez et al., 2018) is a well known free and

open source trafﬁc simulation package which has

been used for experimentation purposes in liter-

ature (and we also use in this paper). We use

SUMO strategy to refer to the default lane change

strategy implemented within the simulator.

• ERB (Empty Road Baseline). As the name sug-

gests, it is the time taken by the EV when there

are no vehicles on the road for the entire simula-

tion period. This is the minimum possible time

the EV can take and hence acts as a lower bound

for the EV traversal time.

Figure 1 shows the comparison between EV

traversal time of the above mentioned strategies

which act as a baseline for our work. As shown in the

ﬁgure, BLS outperforms FLS and SUMO, therefore,

in this work we focus on providing a better strategy

than BLS for lane level dynamics. There are two ma-

jor limitations of BLS which we try to overcome in

this work.

• BLS takes the decision of changing lane based on

the computed utility values of each lane. These

utility values are computed based on the current

timestep parameters and as a result can not cap-

ture the long term effect of the decision.

• BLS uses static weights for each parameter which

need to be pre-decided.

In this work, we propose reinforcement learning

based algorithm which can capture the long term ef-

fect of the decisions and does not require any weights

to be assigned to each parameter.

4 MODEL

As mentioned earlier, we encode the lane changing

problem for EV using an RL model. We now describe

each of the components of the underlying MDP tuple:

< S, A,P, R, N >

1. State Space (S). The state space comprises below

parameter values from each lane i:

• x

rel

. Relative distance along the x-axis, i.e., the

difference between the x-coordinate of the po-

sition of vehicle immediately ahead of the EV

on the lane i and the x-coordinate of EV.

• y

rel

. Relative distance along the y-axis, i.e., the

difference between the y-coordinate of the po-

sition of vehicle immediately ahead of the EV

on the lane i and the y-coordinate of EV.

• v

rel

. Relative speed, i.e., the difference between

the current speed of the vehicle immediately

preceding the EV on the lane i and the EV’s

current running speed.

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

136

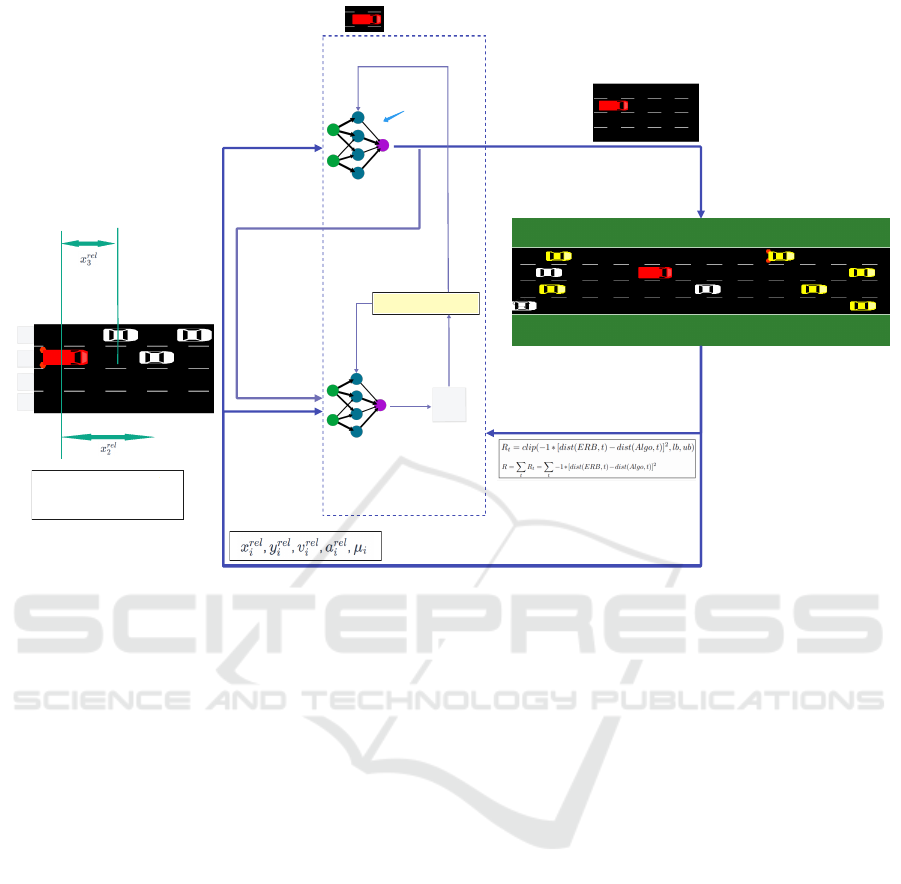
AGENT

ENVIRONMENTActor

Critic

Action

Reward

Next State

State

Action

Adv=Q(s,a)- V(s)

V(S)

EV chooses the lane

at each step

Policy

Closest vehicle ahead of EV in

each lane is considered for

state space

Figure 2: RLLS Algorithm.

• a

rel

. Vehicle acceleration of the vehicle imme-

diately ahead of the EV on the lane i.

• µ

. Free space on the lane i within communica-

tion distance c

. It is calculated similar to the

BLS strategy as described in the Section 3.

As described above, the state space consists of

parameters extracted from vehicles immediately

preceding the EV, with one vehicle chosen from

each lane. The rationale for selecting a preceding

vehicle is to generalize the lane behavior by eval-

uating the parameters of vehicles ahead of the EV.

For N lanes, the state space will consist of 5*N

parameters.

2. Action Space (A). The action space encompasses

the available lane options within the simulation

environment,i.e. it is one of the N lanes.

3. Transition Probability (P). It is the probability

of transitioning from state s

to state s

on taking a

lane change action a. The transition model is not

known and hence we use reinforcement learning

to learn the policy for EV.

4. Reward (R). The intermediate reward at each

timestep is given by:

= −1 ∗ [dist(ERB, t) − dist(Algo, t)]

where dist(ERB,t) is the distance covered by

Empty Road Baseline within a Reward Interval t

and dist(Algo,t) is the distance covered by the al-

gorithm within the same Reward Interval t. The

total episodic reward is the sum of individual

rewards and can be represented using following

equation:

R =

∑

−1∗[dist(ERB, t)−dist(Algo, t)]

To mitigate the effect of outliers on the reward

computation, hyperparameters such as the lower

bound (lb) and upper bound (ub) are employed

to clip the intermediate reward. The selection of

appropriate values for lb and ub is determined

through experimentation, reﬂecting the adjust-

ment of these parameters to optimize the reward

calculation process.

= clip(R

, lb, ub) (1)

5. Total Lanes (N). Represents the total number of

lanes. At any point, each vehicle will be present

in one of the N lanes.

Improving Lane Level Dynamics for EV Traversal: A Reinforcement Learning Approach

137

5 RLLS: REINFORCEMENT

LEARNING BASED LANE

Our RLLS approach uses A2C (Advantage Actor-

Critic) as an underlying algorithm to solve the model

described in Section 4. A2C is a synchronous, de-

terministic variant of Asynchronous Advantage Ac-

tor Critic (A3C) (Mnih et al., 2016). It combines

elements of both the actor-critic architecture and ad-

vantage estimation to improve training stability and

efﬁciency. This hybrid architecture combines value-

based and policy-based methods that help to stabilize

the training by reducing the variance. an Actor re-

sponsible for controlling the agent’s behavior (policy-

based method) and a Critic assessing the quality of

the actions taken (value-based method). In A2C, the

actor component is assigned the role of selecting ac-

tions based on the current policy, while the critic part

evaluates the value of state-action pairs and provides

feedback to the actor. The different components of

our RLLS approach are described in Figure 2.

As shown in the ﬁgure, the actor network maps

each state to a corresponding action. We can update

the Actor Network weights after every time step. The

actor network outputs a probability distribution cor-

responding to each action. We sample actions from

this probability distribution according to each action’s

probability. In our case, the action corresponds to the

lane on which EV should travel. If the action to take

lane1 has a value of .8 and the action to take lane2

has a value of .2, we will only choose the lane1 action

80% of the time and the lane2 action 20% of the time.

Because the output is a probability distribution, please

note that the agent action will not be deterministic but

stochastic.

A2C algorithm uses the Advantage function

which plays a crucial role in stabilizing the learning

process by estimating how better it is to take an ac-

tion at a state when compared to the average value of

that state. It gauges the additional reward obtained be-

yond the expected value of that state. If the Advantage

function A(s,a) is positive, indicating that our action

performs better than the average value of that state,

our gradient is encouraged in that direction. Con-

versely, if A(s, a) is negative, suggesting that our ac-

tion under performs compared to the state’s average

value, our gradient is prompted in the opposite direc-

tion. This mechanism helps guide the training process

towards actions that yield superior outcomes relative

to the state’s average value.

The critic network maps each state s to its corre-

sponding value v(s). Unlike the Actor Network which

outputs a probability distribution of actions, the Critic

Network outputs the value of the input state as a ﬂoat-

ing point number. In the ﬁgure 2, the critic network

evaluates the input state to have a value v(s).

6 EXPERIMENTS

Goal of the experiments section is to compare the per-

formance of our RLLS approach against the leading

baseline strategies across different settings. The met-

ric we use to compare the strategies is the EV traver-

sal time, i.e., the total time taken by the EV to cover

the stretch of the road. RLLS is evaluated against the

following baseline strategies:

• ERB - Empty Road Baseline

• SUMO - Default strategy used within simulator.

• FLS - Fixed Lane Strategy

• BLS - Best Lane Strategy

We propose three variants of RLLS namely

RLLS-A,B and C. Each variant differs from the other

based on the type of reward function used in the sim-

ulation (episodic,intermediate or both) and the train-

ing scenario (trained using normal trafﬁc or the worst

case trafﬁc simulation using slowed down vehicles).

The difference between these variants is summarized

in Table 1.

Table 1: RLLS Settings.

Setting Training Scenario Reward Type

RLLS-A Normal Trafﬁc Intermediate

RLLS-B Normal Trafﬁc

Intermediate +

Episodic

RLLS-C

3 vehicles slowed

for every 10 seconds

Intermediate +

Episodic

6.1 Setup

In this section, we present our experimental set-up us-

ing the SUMO software to evaluate the different EV

strategies. The parameters used for simulation are

listed in Table 2. The experimental setup tries to repli-

cate the environment which is prevalent in major city

area. The road segments in such cities have multiple

lanes that are quite crowded and are in general 1 km

to 10 km in length, at a stretch, before hitting an inter-

section. In our experiments, unless stated otherwise,

we use a 2 km one way stretch of road with 4 lanes.

As discussed in Section 5, we employed the Ad-

vantage Actor-Critic (A2C) model for training. The

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

138

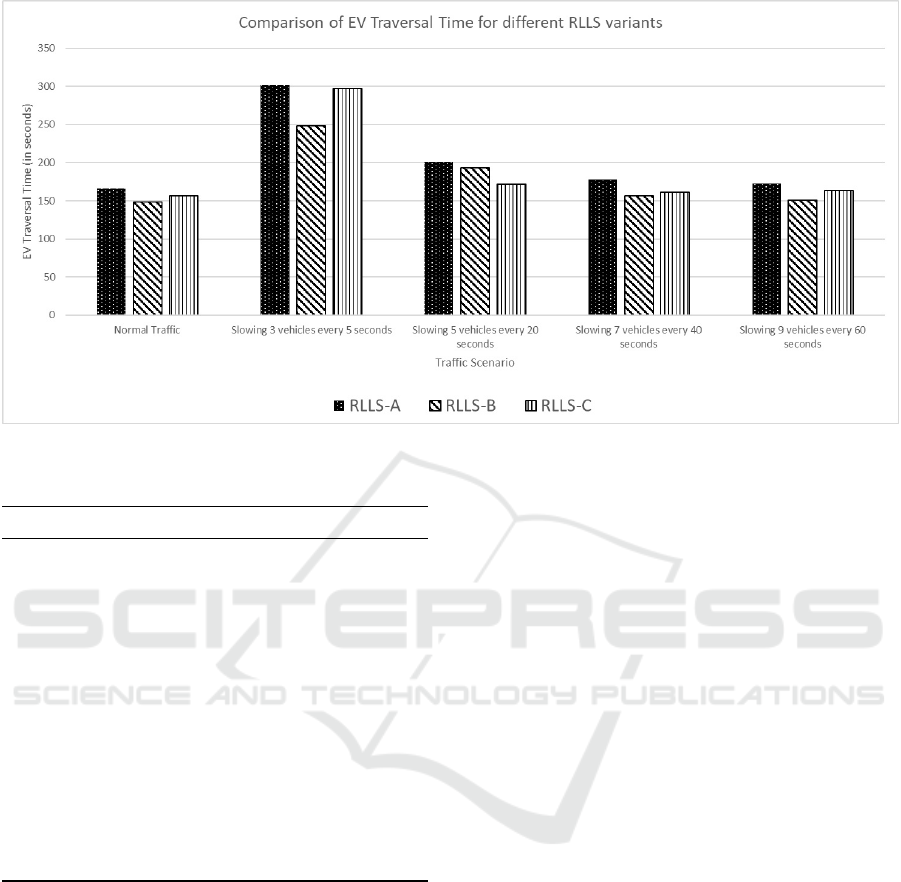
Figure 3: Comparison of EV traversal time for RLLS variants.

Table 2: Experimental Parameters.

Parameters Description Defaults

Vehicle maximum speed 33.33m/s

Preferred maximum speed variable

Vehicle acceleration 0.8m/s

Vehicle deceleration 4.5m/s

Request delay 1 second

dev

Speed deviation 0, 0.2

σ Driver imperfection 0, 0.5

Lowest speed weight-age 0.4

Average speed weight-age 0.4

Free space weight-age 0.2

Min utility difference

between lanes

0.20

t Reward Interval 5 seconds

α Re-computation Interval 10 seconds

Communication Distance 100 meters

intermediate reward is subjected to clipping as men-

tioned in Equation 1. The lower bound (lb)is used

as -100 and upper bound (ub) is used as 0 to ensure

stability during the reinforcement learning process.

The training comprises of 700,000 steps. The train-

ing setup is designed in such a way that the EV ex-

plores through various trafﬁc distributions. The same

simulation environment is used across strategies for

uniformity. At every simulation step, RLLS decides

whether EV should change to any other lane or con-

tinue in the same lane. All the algorithms take lane

change decision for EV at every re-computation inter-

val. EV also communicates to other vehicles within

communication distance to change the lane at every

re-computation interval. The re-computation interval

is ﬁxed to 10 seconds in our experiments (refer Table

2).

6.1.1 Simulation Model Setup for Real World

Dataset

We model the trafﬁc patterns corresponding to cities

with relatively faster moving trafﬁc using the data

available from the City of New York Department of

Transportation(NYCDOT) (NYD, 2022). The NYC-

DOT data feed contains real-time trafﬁc information

from sensor feeds, mostly from major arterials and

highways of New York City (NYC). This data feed is

updated every minute for each road over a total of 137

roads. We developed our simulation model using the

following steps:

1. We collected data for about a week (9670 min-

utes) from the real-time data feed.

2. For any road simulated, a segment of 2 kms is

used, irrespective of the actual length of the road

segment.

3. For (a few) roads with varying number of lanes

(merges or splits), we use the maximum number

of lanes for the entire length we simulate.

4. We included 131 roads having 4 lanes each (roads

having other number of lanes were excluded).

5. The road speed data we have is converted into in-

dividual lane speed using the procedure described

below that would capture the salient features of

NYC trafﬁc.

6. Modeling Groups. Firstly, we classify roads into

groups based on number of lanes in the road.

Improving Lane Level Dynamics for EV Traversal: A Reinforcement Learning Approach

139

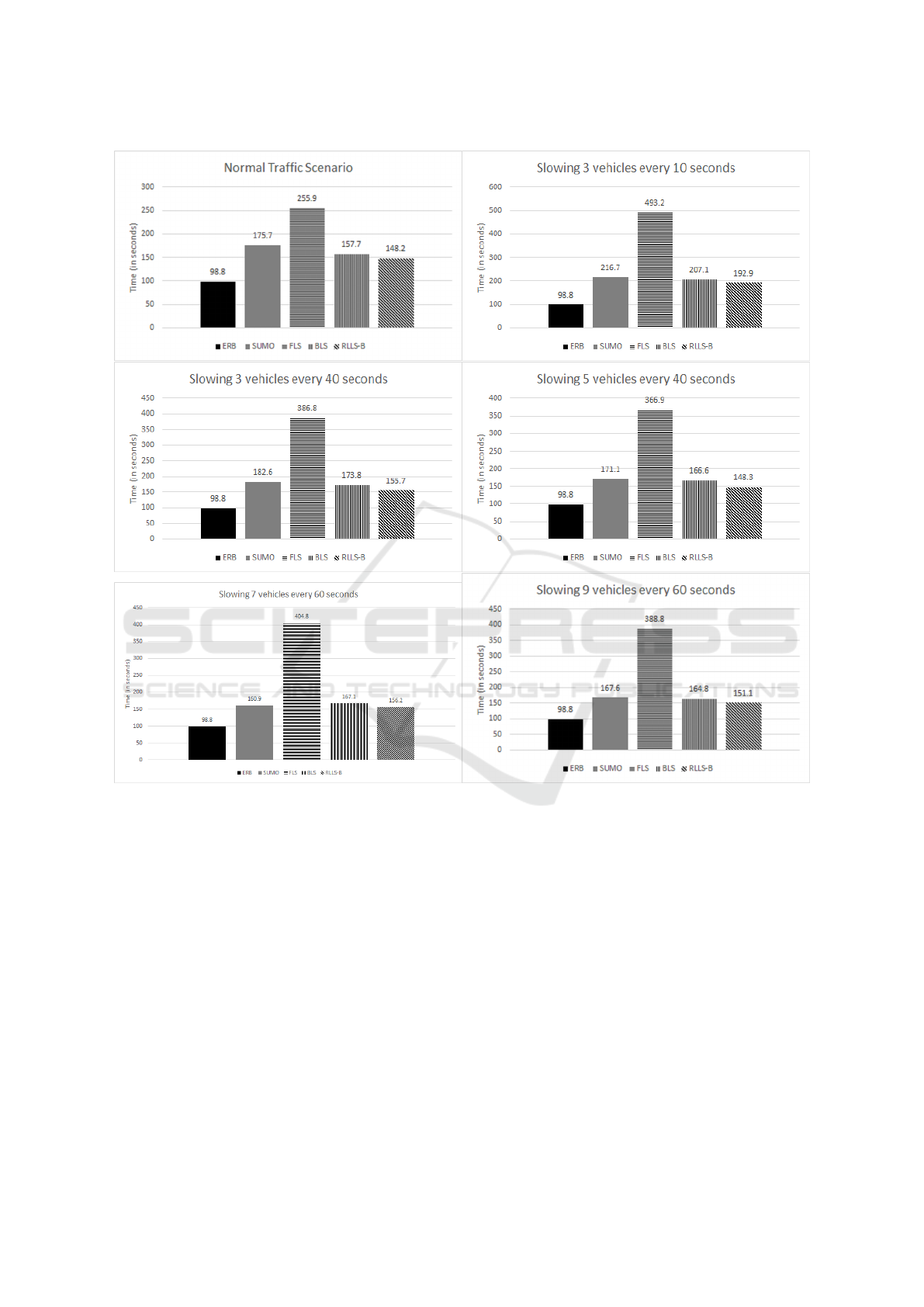
Figure 4: Comparison of EV traversal time of RLLS with baseline strategies in different trafﬁc scenarios.

Hence all roads with 2 lanes are classiﬁed into one

group g2, roads with 3 lanes into group g3 and so

on. In this work, we consider only roads with 4

lanes so we have a single group g4.

7. Modeling Buckets. For the group g4, the average

road speeds are classiﬁed into buckets using inter-

vals of 5 m/s (18 km/h) each. Therefore we have

buckets b

1 j

for 0-5 m/s, b

2 j

for 5-10 m/s till b

14 j

for 65-70 m/s.The average speed for each bucket,

avg j

, is taken as the mean of the bucket. For ex-

ample, for the bucket 0-5 m/s, the average bucket

speed, b

avg j

is considered 2.5 m/s. In a similar

way the average road speed for 5-10 m/s bucket is

considered 7.5 m/s.

8. Obtaining Weights for Buckets. We then obtain

the weights for each bucket in the following fash-

ion: We have information for 131 roads having

9670 minutes of data collected per minute. There-

fore, for each road, we have 9670 data points cor-

responding to average speed of the road at that

minute. Each of these 9670 points are then classi-

ﬁed into buckets depending on the speed the data

point represents. The weight of a bucket is incre-

mented by 1 for each data point that falls under

this bucket. For example, if the average speed of

a road (with j lanes) is 0-5 m/s for 500 minutes

(out of the 9670 minutes) then we increment the

weight w

1 j

by 500. This procedure is repeated for

all the roads to obtain the total weight for each

bucket.

9. The SUMO Simulation. Each b

i j

has an aver-

age bucket speed b

avg j

and a weight w

i j

. b

avg j

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

140

is taken as the average road speed in simulation.

To simulate lanes, b

avg j

is converted into lane

speeds: Each lane is set a maximum speed, picked

using a uniform distribution between b

i j

± 40%.

Hence, the mean of maximum speed across lanes

is the average road speed on expectation. We then

let the EV traverse on a 2 km stretch of road in

the SUMO simulation and calculate it’s run time.

Each setting is run for 100 times, hence the same

lane will have different maximum speeds across

the 100 runs and we obtain 100 different EV run

times.

10. EV Run Time per Bucket. We average the 100

different EV run times obtained to compute the

EV run time EV

ri j

for a bucket i and group j. It

represents the time an EV would take (on average)

if the number of lanes is j and the average road

speed corresponds to b

avg j

. This is repeated for

all buckets in every group.

11. Computing Mean Run Time. For each group

j, we compute gr

= EV

r1 j

∗ w

1 j

+ EV

r2 j

∗ w

2 j

... + EV

r14 j

∗w

14 j

1 j

+...+w

14 j

)

represents the av-

erage time an EV needs to travel a 2 km road

with j lanes. As we consider only a single group

with 4 lanes, the mean run time is obtained as

+...+w

144

)

. This mean run time represents the

average time an EV needs to cover a 2 km stretch

of road with speeds corresponding to NYC roads

and is used as run time for different strategies.

6.1.2 Trafﬁc Scenarios

In our experiments we consider different trafﬁc sce-

narios to evaluate the performance of our approach.

• Normal Trafﬁc: This is the regular trafﬁc scenar-

ios where vehicles are travelling on the road. In

the simulation, at each second one vehicle enters

the road with a probability of 60%.

• Slowing down m vehicles every t seconds: These

are the specialized trafﬁc scenarios which we in-

troduce to simulate trafﬁc congestion on the road.

In this scenario, every t seconds, we randomly

slow down m vehicles on the road. This can be

considered as worst case scenarios as it is difﬁcult

to move in a congested road where vehicles are

moving at a very slow pace. Therefore, if an al-

gorithm performs well in such scenarios it can be

considered robust to random trafﬁc congestion’s

which can occur in real-world.

6.2 Results

Our ﬁrst experiment is to compare the results of dif-

ferent variants of our approach i.e., RLLS in different

trafﬁc scenarios to identify the best performing vari-

ant. Figure 3 shows the comparison of EV traversal

times in different trafﬁc conditions. As shown in the

ﬁgure, RLLS-B outperforms the other variants and

has lowest EV traversal time across different settings.

We can make following observations from these re-

sults:

• Providing both intermediate and episodic reward

helps in learning a better model than providing

only the intermediate reward.

• We can train a single model for normal trafﬁc sce-

narios and it generalizes well to different trafﬁc

conditions.

Next, we provide the comparison of RLLS-B

model against baseline approaches on the synthetic

dataset. Figure 4 show the comparison of the time

taken by EV using RLLS-B and other approaches. As

shown in the ﬁgure, RLLS-B consistently performs

better than existing approaches for different scenar-

ios. Here are the key observations:

• BLS outperforms SUMO in minimizing the EV

traversal time through its utility function com-

putation in normal trafﬁc conditions. However,

when the environment is made more complex,

like slowing vehicles; the performance of BLS

gets limited with only a little improvement over

SUMO. This could be due to its deterministic na-

ture. In contrast, by utilizing the adaptability of

the RL algorithm, the RLLS-B algorithm can dy-

namically respond to these varying trafﬁc scenar-

ios using the state space information.

• In normal trafﬁc scenarios, RLLS-B obtains 6%

improvement over BLS but in specialized scenar-

ios of slowing down vehicles this improvement

goes up to 10.9% (Slowing down 5 vehicles ev-

ery 40 seconds)

Finally, in Figure 5, we present the comparison of

RLLS-B approach with the baseline strategies on the

real-world dataset. The data is processed and the run-

time of EV is computed as mentioned in the Sec-

tion 6.1.1. In this case as well, RLLS-B outperforms

BLS and other baseline strategies. In the normal traf-

ﬁc scenario, RLLS-B obtains 2.5% improvement over

BLS which increases to 4% when we slow down ve-

hicles.

It is important to note that even a very small im-

provement in the travel time of EV can help in saving

human lives, so improvement of 4% is of signiﬁcant

importance.

Improving Lane Level Dynamics for EV Traversal: A Reinforcement Learning Approach

141

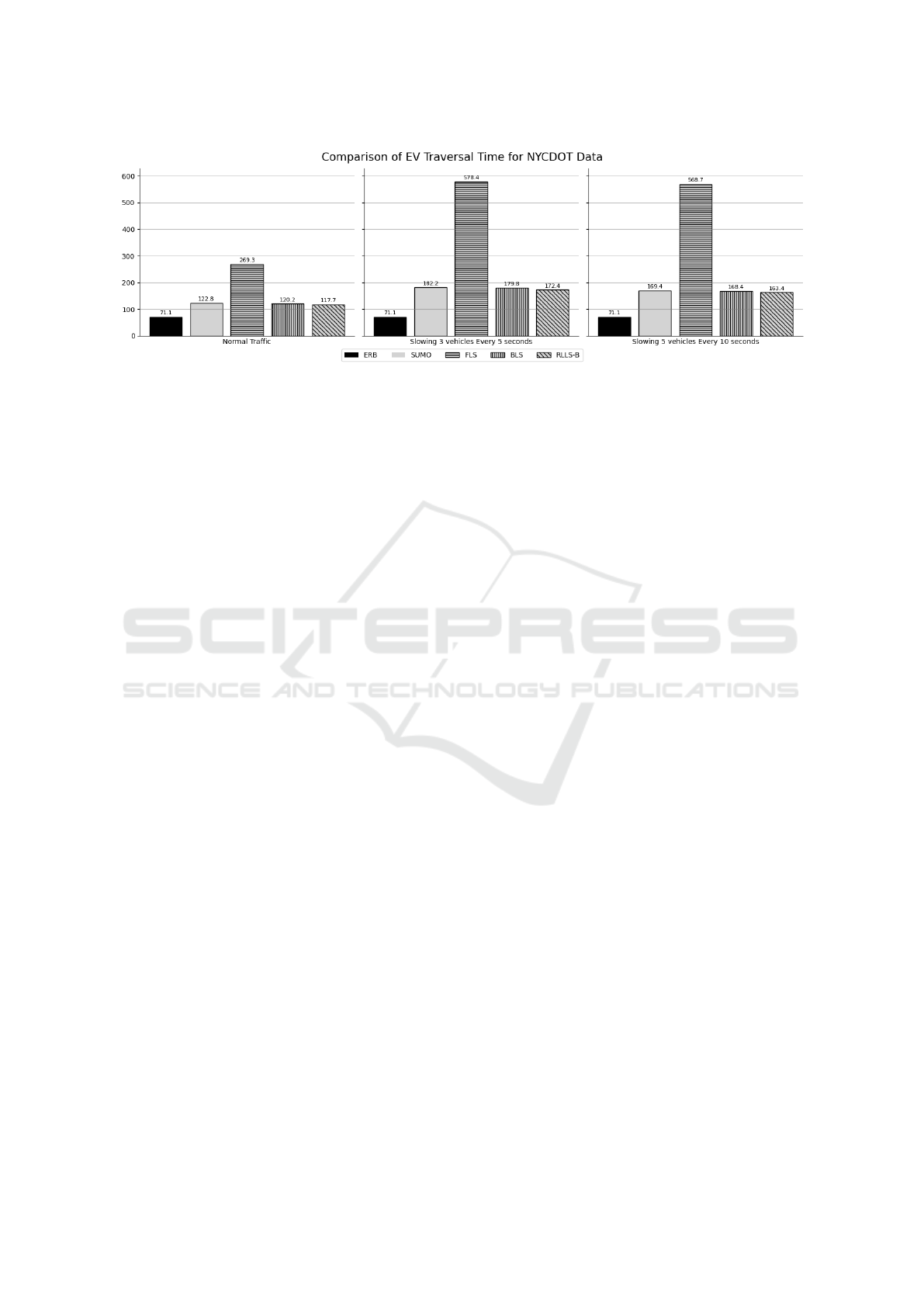
Figure 5: Comparison of EV Traversal Time for ERB, SUMO, FLS, BLS, RLLS-B strategies for Real-World dataset.

We would also like to highlight that the perfor-

mance of RLLS-B can be improved by choosing a

better state space. Initially we experimented with a

bigger state space including the details of 20 clos-

est vehicles around EV but this state space resulted

in sub-optimal results and also increased the training

time. The algorithm performance has been enhanced

by adjusting this state space to include the positional

difference and speed, acceleration differences of the

immediate vehicle only in each of the four lanes; as

well as the free space. This reduction in the dimension

resulted in not only reducing the noise from the initial

state space, but also focusing on more relevant factors,

leading to improved performance of the RLLS-B lane

changing strategy.

7 CONCLUSION

In this paper we presented a reinforcement learning

strategy to improve lane level dynamics for emer-

gency vehicles. Through detailed experiments us-

ing SUMO simulator, we showed that our approach

outperforms the baseline strategies in different trafﬁc

scenarios. We considered a straight stretch of road in

this work. In future, we would like to extend this work

to combine the route planning and lane level dynam-

ics which can further help in reducing the overall EV

travel time.

REFERENCES

Agarwal, A. and Paruchuri, P. (2016). V2v communication

for analysis of lane level dynamics for better ev traver-

sal. In 2016 ieee intelligent vehicles symposium (iv),

pages 368–375. IEEE.

Asaduzzaman, M. and Vidyasankar, K. (2017). A priority

algorithm to control the trafﬁc signal for emergency

vehicles. In 2017 ieee 86th vehicular technology con-

ference (vtc-fall), pages 1–7. IEEE.

Cao, W. and Zhao, H. (2022). Lane change algorithm us-

ing rule-based control method based on look-ahead

concept for the scenario when emergency vehicle ap-

proaching. Artiﬁcial Life and Robotics, 27(4):818–

827.

Chen, C., Wei, H., Xu, N., Zheng, G., Yang, M., Xiong,

Y., Xu, K., and Li, Z. (2020). Toward a thousand

lights: Decentralized deep reinforcement learning for

large-scale trafﬁc signal control. In Proceedings of

the AAAI Conference on Artiﬁcial Intelligence, vol-

ume 34, pages 3414–3421.

Chu, T., Wang, J., Codec

a, L., and Li, Z. (2019). Multi-

agent deep reinforcement learning for large-scale traf-

ﬁc signal control. IEEE Transactions on Intelligent

Transportation Systems, 21(3):1086–1095.

Ghosh, S. and Varakantham, P. (2018). Dispatch guided

allocation optimization for effective emergency re-

sponse. In Proceedings of the AAAI Conference on

Artiﬁcial Intelligence, volume 32.

Giri, A. R., Chen, T., Rajendran, V. P., and Khamis, A.

(2022). A metaheuristic approach to emergency ve-

hicle dispatch and routing. In 2022 IEEE Interna-

tional Conference on Smart Mobility (SM), pages 27–

31. IEEE.

Haghani, A., Hu, H., and Tian, Q. (2003). An optimiza-

tion model for real-time emergency vehicle dispatch-

ing and routing. In 82nd annual meeting of the Trans-

portation Research Board, Washington, DC. Citeseer.

Ismath, I., Samarasinghe, T., Dias, D., Wimalarathna, M.,

Rasanga, W., Jayaweera, N., and Nugera, Y. (2019).

Emergency vehicle traversal using dsrc/wave based

vehicular communication. In 2019 IEEE Intelligent

Vehicles Symposium (IV), pages 1981–1986. IEEE.

Joe, W., Lau, H. C., and Pan, J. (2022). Reinforcement

learning approach to solve dynamic bi-objective po-

lice patrol dispatching and rescheduling problem. In

Proceedings of the International Conference on Au-

tomated Planning and Scheduling, volume 32, pages

453–461.

Jotshi, A., Gong, Q., and Batta, R. (2009). Dispatching and

routing of emergency vehicles in disaster mitigation

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

142

using data fusion. Socio-Economic Planning Sciences,

43(1):1–24.

Lopez, P. A., Behrisch, M., Bieker-Walz, L., Erdmann, J.,

otter

od, Y.-P., Hilbrich, R., L

ucken, L., Rummel,

J., Wagner, P., and Wießner, E. (2018). Microscopic

trafﬁc simulation using sumo. In 2018 21st inter-

national conference on intelligent transportation sys-

tems (ITSC), pages 2575–2582. IEEE.

Maleki, M., Taghavipour, A., and Azadi, S. (2023). A real-

time optimal cooperative lane change strategy via v2v

communication. Proceedings of the Institution of Me-

chanical Engineers, Part D: Journal of Automobile

Engineering, 237(13):3094–3107.

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,

Harley, T., Silver, D., and Kavukcuoglu, K. (2016).

Asynchronous methods for deep reinforcement learn-

ing. In International conference on machine learning,

pages 1928–1937. PMLR.

NYD (2022). New york department of transporta-

tion - real-time trafﬁc speed data. https://data.

cityofnewyork.us/transportation/real-time-trafﬁc-

speed-data/xsat-x5sa.

Puterman, M. L. (2014). Markov decision processes: dis-

crete stochastic dynamic programming. John Wiley &

Sons.

Schmid, V. (2012). Solving the dynamic ambulance reloca-

tion and dispatching problem using approximate dy-

namic programming. European journal of operational

research, 219(3):611–621.

Su, H., Zhong, Y. D., Dey, B., and Chakraborty, A. (2022).

Emvlight: A decentralized reinforcement learning

framework for efﬁcient passage of emergency vehi-

cles. In Proceedings of the AAAI Conference on Arti-

ﬁcial Intelligence, volume 36, pages 4593–4601.

Van der Pol, E. and Oliehoek, F. A. (2016). Coordi-

nated deep reinforcement learners for trafﬁc light con-

trol. Proceedings of learning, inference and control of

multi-agent systems (at NIPS 2016), 8:21–38.

Zhang, S., Deng, G., Yang, E., and Ou, J. (2022).

Optimal vehicle lane change trajectory planning in

multi-vehicle trafﬁc environments. Applied Sciences,

12(19):9662.

Improving Lane Level Dynamics for EV Traversal: A Reinforcement Learning Approach

143